基于核心素养下的试卷命制方法与策略

福建省莆田市秀屿区毓英中学 林 琴

数学试卷命题是一项具有复杂性、技术性的工作项目，对于数学任课教师来讲，在教学中讲解数学题目时，基本应用的都是完整的试题，这能充分体现出教师较强的解题能力。但是，命题需要教师将知识、方式、水平、能力都落实在实际题目中，将各个题目进行整合、优化，从而生成一份完整的试卷。这就需要教师从研究者的角度出发，在审题、制题的过程中，重视每一个细节，掌握有效命题途径。

一、基于核心素养下的初中数学试卷命制的原则

1.公平原则。

公平原则意味着学科试题的参考材料和学术背景必须包括每个学生都有可能正确理解的生活状况、社会上的现实、数学上的现实或其他各种学术上的现实。公平考虑受到考生由于性别等社会因素不同造成的综合认知能力差异，没有规定需要特殊学科专业学术背景学生才能正确理解的考试科目。

2.现实性原则。

现实性试题泛指在进行构建教学试题时，所需要使用的教学材料内容应充分来源于学生所熟悉的现实，特别是当前作为构建试题主要材料的一些社会经济热点和国际焦点社会问题，可以有效丰富广大学生的学习体验，引起广大学生对国家、社会、人类、世界和人民生活的高度关注，让广大学生充分感受我国社会文明不断进步，感受社会与时俱进的良好时代文化氛围。

3.有效性原则。

有效性指初中试题的数学生命规律系统必须充分突出实际数学在社会现实生活中的有效性和应用。通过数学设置适当的现实背景数学信息，引导初中学生通过观察、实验、操作、猜想、验证、推理等多种方式深入分析和正确判断实际数学问题，运用实际数学中的观点和数学方法来解决实际数学问题和解决相关基础学科的实际数学研究问题，从而真正有效提高初中学生的自然环境生态适应能力和人类社会综合生存能力。

4.创新性原则。

创新意味着一个命题应该在稳定时寻求变化，在变化时寻求创新，并以新的方式力求完善。它在内容、形式、结构、场景、提问方式等方面都不同于传统的提问，为学生提供了创新和施展才华的机会，同时也检验了学生的学习能力。

二、基于核心素养下的初中数学试卷命制和评价策略

作为一名数学教师，提出一个教学命题无疑是不可避免的，这不是一项容易的教学任务。但要制作一份合适的数学试卷并不容易。在许多初中生的数学教学工作实践中，一些数学教师不能独立地自己编制制作出一套适合自己的数学试题，存在着教学水平和解题能力上的重大缺陷。我将谈谈根据自己的教育工作学习实践以及制作初中数学试卷的基本技巧和使用方法。

1.立足基础知识、能力以及方法，促进学生核心素养提升与发展。

例1：佳佳水果店2020 年六月份到十二月份的销售情况为450 千克、440 千克、420 千克、480 千克、580 千克、550 千克，这组数据的极差是（ ）。

例 2：一个样本为 1、3、2、2、a、b、c。已知，这一组数据的样本众数是3，平均数是2，这组数据的方差是（ ）。

命制途径：在对以上两个题目进行命制的过程当中，教师可以充分的将教材当中的练习题作为重要的素材和依据，通过相应的组合以及改造而完成。以上两道题主要是围绕着方差、极差以及平均数和众数等一些相关的基本概念而设计出来的，其主要的目的是能够更好地针对学生的核心概念以及基础知识的掌握情况进行考查。针对这样的考题，学生只需要针对教材当中的一些核心内容以及基础知识等进行理解和掌握就可以。

命制反思：以上的两个题目都是从基本方法、核心内容以及基础知识等方面进行命制的，所以，在实际的教学当中，教师应该正确地引导学生针对相关的概念以及知识点的本质进行有效的理解和掌握，进而能够促使学生更加深刻的理解数学法则、数学定理以及数学公式等，并且能够在实际的学习当中进行灵活、有效的引用，同时，应该善于将所学习和掌握的数学知识进行有效归纳和总结，针对数学知识的脉络进行有效整理，进而促使学生能够形成一个较为完整的数学知识体系。另外，在对试卷进行命制的过程当中，教师还应该重视学生对于基本方法、核心内容以及基础知识的回顾和复习，不断的进行巩固，不能够因为图“快”，而片面的追求求解偏题、怪题、难题，否则就会得不偿失。同时，还可以运用教材当中的习题以及例题等进行编制和改造，这样能够引导“教”与“学”去重视教材内容，这些对于促进“教”与“学”的共同发展具有非常重要的作用和意义。

2.立足学生知识技能与生活实际，促进学生核心素养提升与发展。

例3：学校的操场上有一面由24 个边长x 厘米的正方形瓷砖拼成的长方形墙面，现在准备将这个墙面作为学生美术作品展览墙，要求使用面积不能够超过整个墙面的。

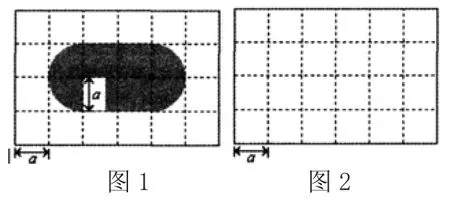
（1）玲玲设计一个方案（如图1 所示），作品展览墙左右两个边是两个半圆，中间是4 个校的正方形，请问：玲玲所设计出来的方案符不符合要求？请你通过计算进行说明。

（2）根据这些已知条件，你能不能也涉及出一个符合以上要求的作品展览墙？请将你的设计方案绘制在图2 的长方形当中，并且标出相应的尺寸（可以不进行计算说明）。

例4：如图3 所示是一座拱桥的横切面图，呈一个抛物线形状，当水位处于正常水位的时候，水面的宽AB 为26 米，当水位上涨1 米的时候，拱桥的水面宽CD为24 米。将AB 所在的直线作为x 轴，抛物线的对称轴作为y 轴，构建一个直角坐标系。

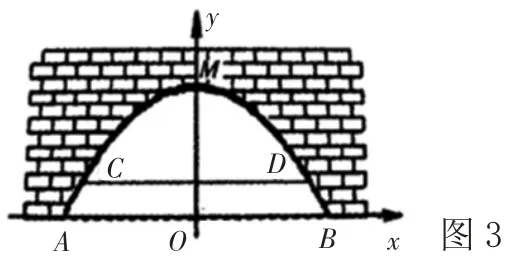
（1）求出这个抛物线的解析式；

（2）通过相应的测算，水面距离拱桥的顶端为1.5 米的时候是警戒水位，当洪水来到的时候，工程工作人员使用仪器测量水面的宽度为10 米，请你帮助工作人员计算一下，这时候的水面有没有超过警戒水位？

命制途径：以上两道题目渗透了浓浓的生活化元素，并且教学导向非常的清晰，能够更好地帮助教师在实际的教学当中重视学生对于活动经验的有效积累。例3 所考查的就是学生对于平面几何以及整式相关知识的有效应用，并且要求学生能够相应的计算获得最终的结果，进而进行具有较强开放性的设计与判断。例4 所考查的就是学生对于二次函数模型的构建、使用二次函数性质与图像去解决一些实际的问题，并且在解决相同类别问题的时候，应该先针对已知条件进行理清，之后针对其中包含的数量关系进行寻找，同时构建相应的数学模型，这些主要是考查学生对于数学知识的“学以致用”能力。

命制反思：新课程改革以及素质教育背景下，要求课堂教学的开展应该更加具有“情境化”和“生活化”，而适当的形式化是初中阶段数学教学开展应该具备的重要特点，因此，在进行试题命制的过程当中，应该重视将“数学化”与“生活化”进行融合和统一。通过“情境化”“生活化”试题的设计，主要考查学生的探究意识以及数学知识的应用意识，还能够考查学生对于数学模型的构建，并且将其转化成为相应的数学问题，针对数学方法以及数学知识进行综合应用，有效解决数学问题的方法以及思想的能力，能够更好的帮助学生掌握正确学习的方法和技巧，进而帮助学生加深对于数学知识的生活感悟。

3.立足课堂教学中问题情境创设，促进学生核心素养提升与发展。

例5：如图4 所示，这个几何体是由8个大小相同的立方块搭成的，几何体的三视图都是2×2 的小正方形。如果在原本的基础上拿掉x 个小立方块之后，保证几何体不倒掉的基础上，几何体的三视图依然都是2×2 的小正方形，最多可以拿掉（ ）个小立方块。

A.1 B.2 C.3 D.4

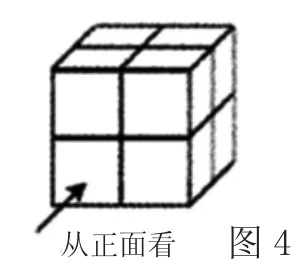
命制途径：关于立体图形的三视图传统命制大多都是“如何辨别几何体的三视图”，但是，例5 的命制关键就是对于命题的视角进行转变，充分体现在实际的数学实践操作当中深刻体会几何体三视图之间存在的联系，进而能够考查学生对于几何体三视图实质性的有效理解和掌握，并且考查学生的合情推理意识以及空间想象能力。

例6：如图5 所示，一把伞垂直于水平地面，当伞收紧的时候，动点P 与点A重合，当伞慢慢打开的时候，动点P 由点A朝着点B 移动，当动点P 到达点B 的时候，伞张开的最大，已知，伞在撑开的过程当中，总有PM=PN=CM=N=6 分米，CE= CF=18 分米，BC=2 分米，假设 AP=x分米。

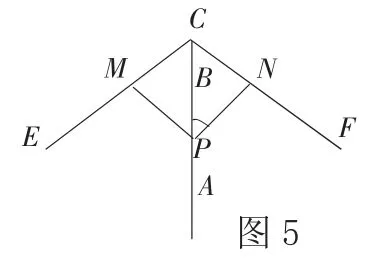
（1）求x 的取值范围；

（2）如果∠CPN=60°，求 x 的值；

（3）假设阳光直射的时候，伞下的阴影面积是y（设定这个阴影是圆面），求x与y 之间的关系式。

命制途径：例6 是直接取材于学生实际生活当中比较常见的雨伞，将具有较强生活化的内容转变得更加具有数学化，图文并茂，考查学生对于相似形、菱形等方面知识点的综合性运用，最终考查学生解决方程的能力，更加重要的是考查了学生对于数学知识的学以致用意识和能力，促使学生能够更加深刻的体会生活当中的数学。

命制反思：引导学生在进行学习的过程中探索数学规律，深刻体会知识形成的一个过程，在针对数学知识进行深层次思考的基础上，更好培养学生对于数学知识的应用意识和能力，以此来更好的培养和发展学生数学思维。通过这样的方式能够促使学生在解决问题过程当中“学”数学、“用”数学、“品”数学、“感”数学，深刻体会数学知识学习的趣味性，这样不仅考查了学生的学习结果，还考查了学生的情感、态度以及价值观，充分地体现出了对于“教学目标”的考查目的。

4.立足学生学习的自主思考探究，促进学生核心素养提升与发展。

例7：如图6 所示，在正方形ABCD 当中，M 是 BC 边上的任意一点，P 是 BC 延长线上的一点，N 是∠DCP 平分线上的一点，如果∠AMN=90°，求证：AM=MN。以下是给出的证明思路，可以依照这个思路开展求证，也可以按照自己的思路开展求证。

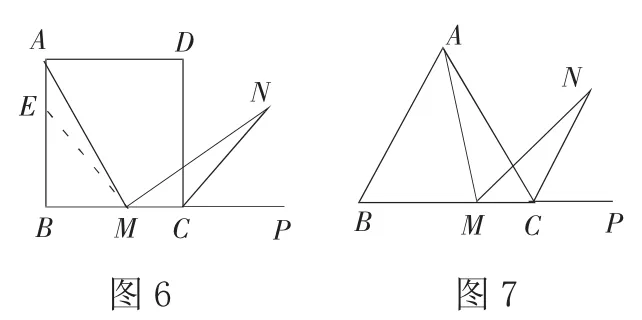
（1）证明：在边 AB 上截取 AE=MC，连接ME，在正方形ABCD 中，∠ABC=∠BCD=90°，AB=BC，所以，∠NMC=180°-∠AMN-∠AMB=180°-∠ABC-∠AMB=∠MAB=∠MAE。（请你根据以上证明过程完成余下的证明过程。）

（2）如果将问题（1）当中的“正方形ABCD”转变为“正三角形 ABC”，如图 7所示，N 是∠ACP 平分线上的一点，那么当∠AMN=60°时，AM=MN 是不是依然成立，请你说一说理由。

（3）如果将问题（1）当中的“正方形ABCD”转变为“正 n 边形 ABCD…X”，请你进行合理的猜想，当∠AMN=（ ）时，AM=MN 依然成立。

命制途径：这道题的设计意图是促使学生能够通过自身的观察、探索、思考以及实验等学习活动进行相应的数学猜想，并且去证明猜想所具有的合理性。考查学生合理的使用数学语言进行数学思考的过程以及进行有条理地表达的能力，促使学生能够更好地掌握数学知识，发现这其中所包含的数学现象。

命制反思：在对试题进行命制的过程当中，要求教师不仅应该充分体现出数学所具有的较强文化性以及工具性，促使学生能够更加深刻地体会数学的理性以及应用性。因此，在实际的教学当中，教师应该有目的性、有针对性地进行思维训练，促使学生能够学会进行数学思考，提升学生对于问题的判断和分析能力，培养学生的创新意识。

结束语

综上所述，新课改的教育理念下，初中阶段的数学试题命题是一项复杂性、实验性的工作。所以，从初中数学教师的角度来看，命题是必须要具备的基础技能。有效的命题，能促进教师反思课堂教学，能促使教师认识到自身教学存在的问题和不足，进而采取有效的措施进行完善和改进，促使自身教学水平提升，让教学质量随之提升。