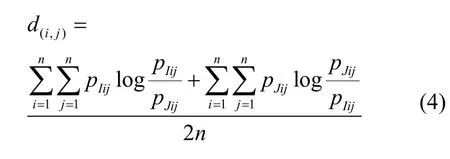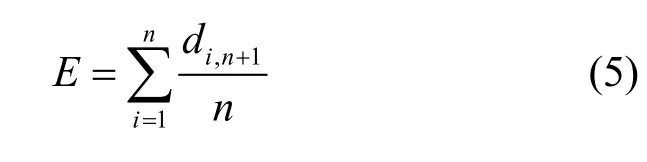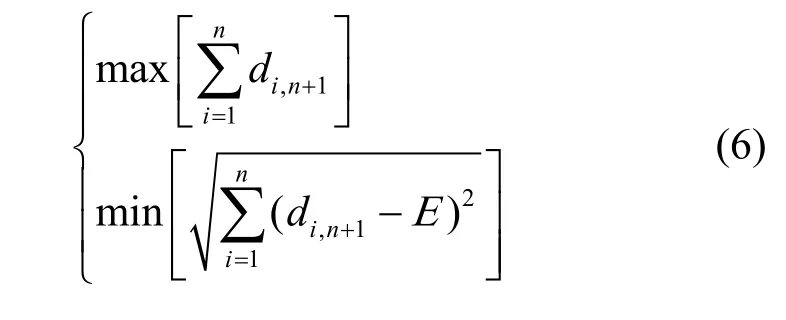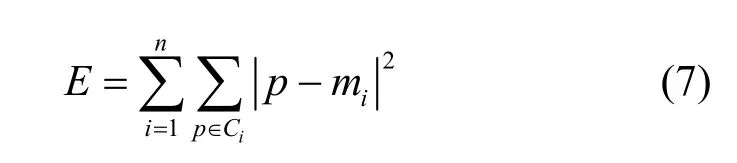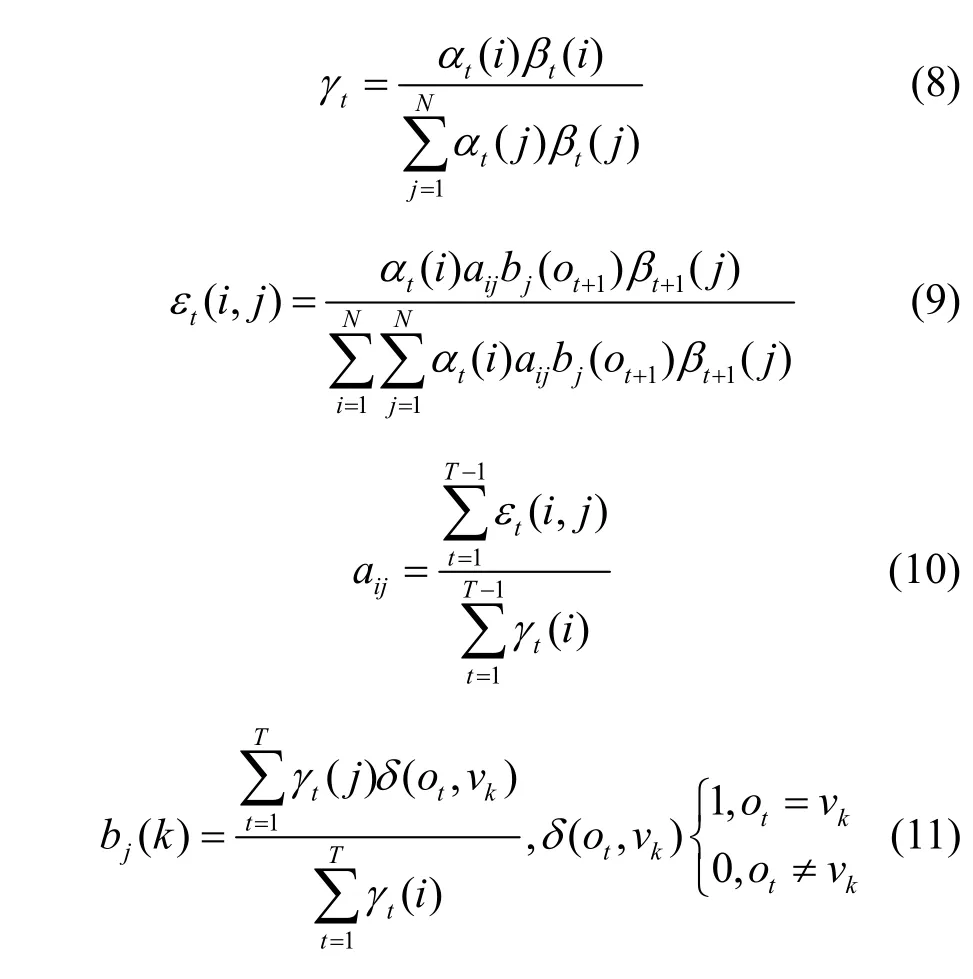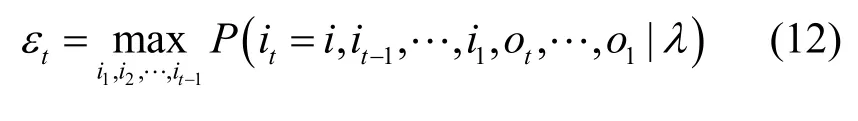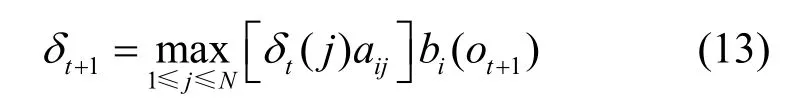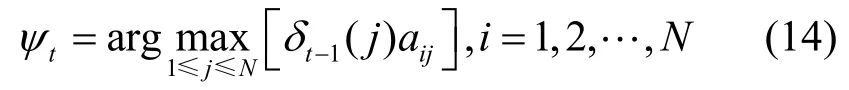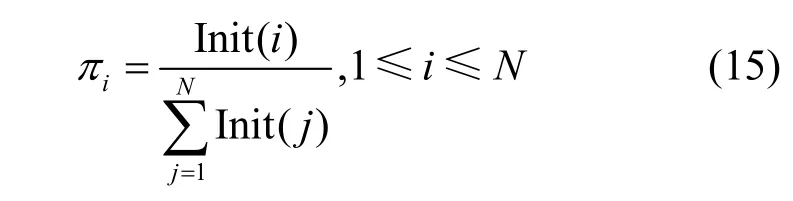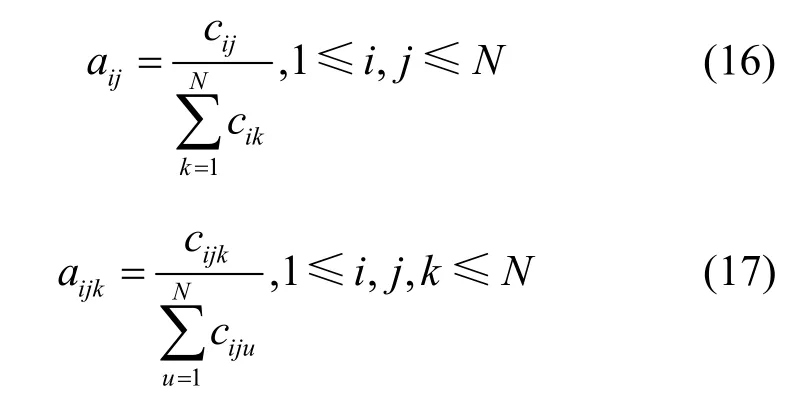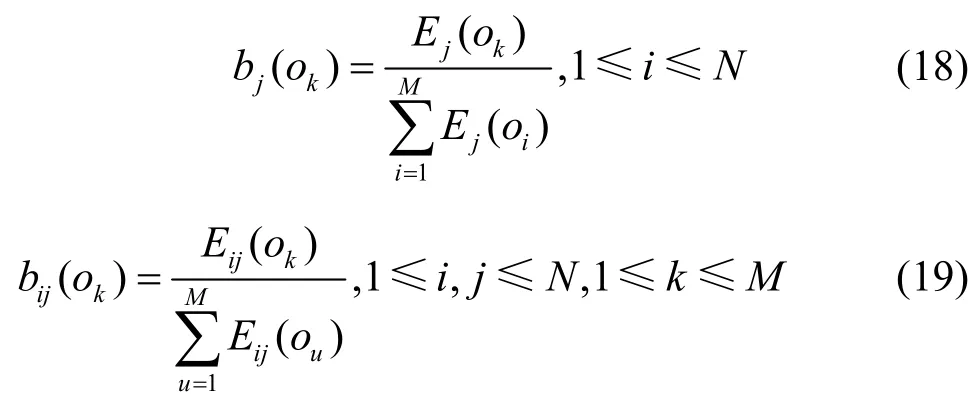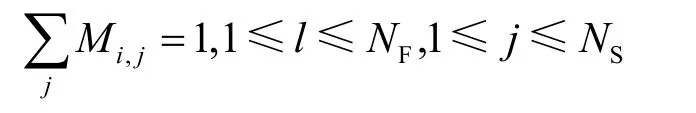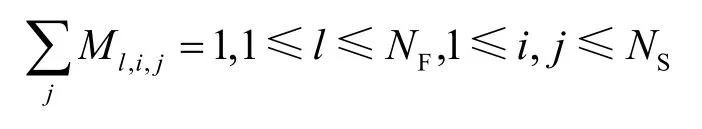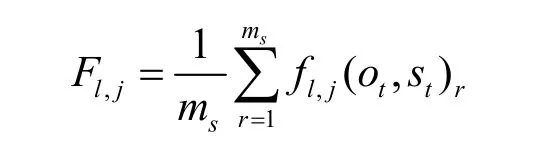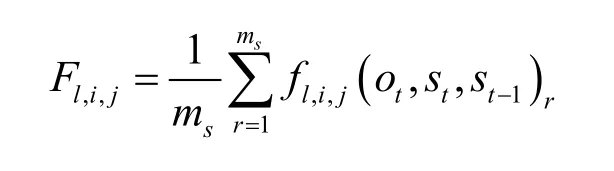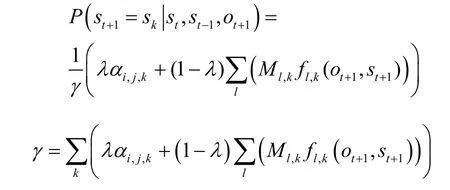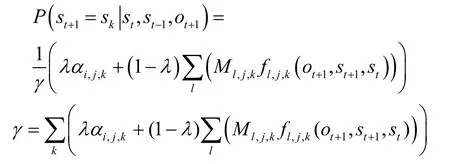钱榕,许建婷,张克君,董宏宇,邢方远
(1.北京电子科技学院网络空间安全系,北京 100070;2.西安电子科技大学计算机科学与技术学院,陕西 西安 710071)
0 引言
随着网络信息技术的迅速发展,人类社会进入复杂网络时代,人们的生产和生活越来越依赖于以Internet、WWW、通信网络、社会关系网络、经济网络等为代表的复杂网络系统的安全可靠和有效运行。异质网络从拓扑结构上看拥有不同类型的顶点和不同类型的边,更加贴近于客观世界。因此人们对异质网络进行研究具有现实意义和挑战性。
链接预测是复杂网络研究的一个重要方向,旨在根据已知的网络结构和信息,发现和还原网络中丢失的信息,或者预测节点之间未来可能存在的关系[1]。在现实生活中,链接预测已经有很多成功的应用,比如推荐系统,可以给新用户推荐兴趣相近的朋友,或给用户推荐其可能感兴趣的视频;再如疫情传播动力学中,可以还原一些丢失的传播路径。随着异质网络研究的深入,元路径思想给异质网络预测链接的研究提供了新的思路。基于元路径的异质网络链接预测能够考虑不同节点类型及节点之间的关系,更好地提取网络中不同的语义信息,从而大大提高网络链接预测方法结果的精确度。近年来,更多的研究学者将元路径融入异质网络的研究中,如将元路径权重融合到异质网络的表征学习中[2],将元路径与图神经网络结合[3]采样异质邻居节点,使用元路径高效提取异质网络的语义信息[4-5]等。因此,将元路径与隐马尔可夫模型(HMM,hidden Markov model)结合并应用于异质网络的预测有着十分重要的理论意义与应用前景。
本文的主要研究工作如下。
1) 提出基于聚簇的一阶隐马尔可夫模型的链接预测方法,即C-HMM(1)。将HMM 应用于链接预测中,并将数据簇的方法应用于 HMM。对k-means 算法在确定初始聚簇中心时进行改进,得到基于距离均方差最小的方法,使簇中心同时满足到其他簇中心之间的距离之和最大以及与其他所有的簇中心之间距离的均方差最小。
2) 提出基于聚簇的二阶隐马尔可夫模型的链接预测方法,即C-HMM(2),并分析了C-HMM(2)在链接预测上的有效性。C-HMM(2)在考虑模型当前状态的基础上,又合理地考虑了概率和模型历史状态之间的关联性,提高了链接预测的准确率。
3) 提出基于最大熵(ME,maximum entropy)的C-HMM(2)的链接预测方法,即ME-HMM。通过最大熵模型,在链接预测中加入训练数据的特征信息;同时通过C-HMM(2)考虑状态转移概率和观测值输出概率和模型历史状态之间的关联性,进一步提高了链接预测的准确率。
4) 对本文提出的方法与已有的链接预测方法进行实验对比分析。实验结果表明,本文提出的方法优于已有的链接预测方法。
本文方法的研究框架如图1所示,其中C-HMM(1)与C-HMM(2)统称为C-HMM 方法。
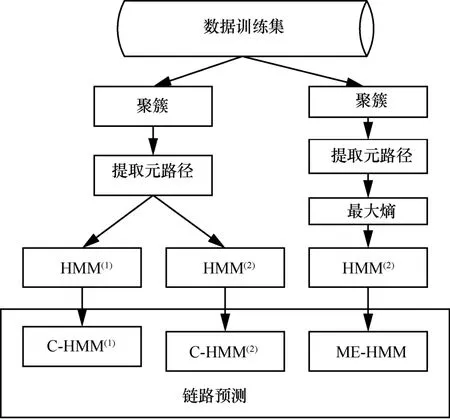
图1 本文方法的研究框架
1 相关工作
基于异质网络中的链路预测问题引起了学者们的广泛关注,目前基于元路径的链接预测研究十分火热。
1.1 异质网络
异质网络[6]是一个带有对象类型映射函数ϕ :ν→ Α和链接类型映射函数 ψ :ε → R 且的有向图 G=(ν ,ε),其中ν 和ε 分别表示网络的节点集合和链接的边集合,Α 和R分别表示网络中的节点类型集合和链接类型集合。本文选用的DBLP(digital bibliography &library project)数据集中选取了论文、作者、会议3 种类型节点,以及作者与论文之间的撰写关系、论文与会议之间的发表关系等。
1.2 元路径
元路径[7]是在异质网络模式上链接两类节点的路径。元路径 P 定义为的形式,它表示节点A1和Al+1之间的复合关系其中,Ai为节点类型,Ri为关系类型,◦为关系间的复合算子。在DBLP 数据集中,作者与作者合作撰写论文关系的元路径可以表示为作者( A)”,如果作者与论文、论文与作者之间没有任何其他的链接关系,则该元路径可以简化为“APA”,语义信息为与指定作者合作的作者。图2为异质网络DBLP 的常见元路径。
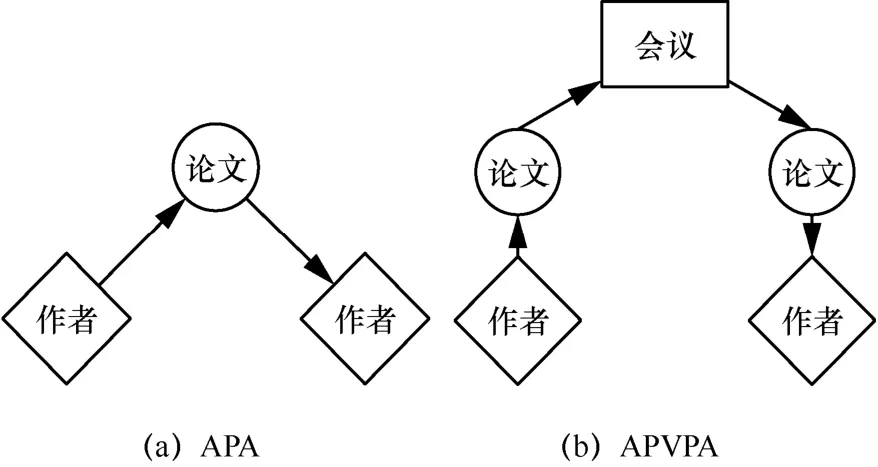
图2 异质网络DBLP 的常见元路径
1.3 链路预测技术
链路预测技术是研究异质网络中重要的研究方向之一。郭振宏等[8]提出对不同元路径综合网络的拓扑特征获得异质和同质数据,再通过逻辑回归作为链路预测模型。韩忠明等[9]提出基于动态网络表示的链接预测(DNRLP,dynamic network representation based link prediction)模型,基于连接强度的随机游走算法模拟网络的动态信息扩散,对新时刻下得到的节点表示通过度量相似度得到预测结果。刘大伟等[10]提出将局部共同邻居集合根据全局最短路径信息进行建模的链路预测算法。董鑫等[11]提出基于Boosting 的异质信息网络链路预测方法,通过选择样本择优的方式和增设阈值分别对Boosting 算法的训练速度和防止过拟合方面进行改进,并通过集成学习的思想改进链路预测性能。赵妍等[12]提出挖掘有效元路径来生成带节点属性的子图,用子图代表被预测链路,用图核方法计算子图相似性,再训练支持向量机得到预测结果。孙诚等[13]提出基于共同邻居(CN,common neighbor)、路径和随机游走的8种常用链路预测指标的线性组合作为度量指标,并找到较好的优化参数,提出相应的神经网络模型。黄立威等[14]分析了异质信息网络不同元路径上不同类型节点和关系的不同语义,并通过不同元路径上节点之间的连接概率进行链接预测。
本文选用易于扩展、可用于大型数据集且最常用的基于相似性指标的CN 方法[15-16]、能够获得大量节点之间的上下文信息的重启随机游走(RWR,restart in random walks)方法[17]、单一的HMM 方法[18],以及近些年学者提出的针对不同类型对象间来凝结关系而重构异质网络的BRLinks 方法[19]、通过将异质网络划分多通道再对其进行图卷积网络学习网络节点的向量表示的MDGCN(multichannel deep graph convolutional network)方法[20]、将异质网络关系预测视为PU 学习问题的PURP(positive and unlabeled relationship link prediction)方法[21],在此只简单介绍CN 和RWR 方法。
1) CN 方法
CN 是最常见的相似性指标之一。CN 指的是2 个节点之间的公共邻居节点。公共邻居节点数目越多,这2 个节点就越有可能产生链接。若节点x的邻居节点集合是 Γ(x),那么节点x和节点y的相似性指标CN 为2) RWR 方法
RWR 是在随机游走方法的基础上改进得到的,其主要原理是从图中的某一节点开始出发,随机选择该节点相邻节点的一个或返回开始的节点。RWR方法有一个重启概率α,而1 -α则表示移动到相邻节点的概率,经过多次迭代达到稳定状态之后结束。RWR 的定义式为
其中,rt=[ri,j]是 n× 1的得分向量,ri,j是节点j到节点i的相关度得分;et是 n× 1的初始向量,第i个元素为1,其他为0。
2 基于聚簇隐马尔可夫的异质网络链接预测
2.1 隐马尔可夫模型
HMM 常用来描述一个含有隐含未知参数的马尔可夫过程。在HMM 中,状态是不直接可见的,可以通过观测序列的随机过程表现出来。HMM 可以用S、 O、π、A、 B 这5 个元素表示。其中,S为隐含状态,O为可观测状态,π 为初始状态概率矩阵,A为隐含状态转移概率矩阵,B为观测状态转移概率矩阵。HMM(1)如图3 所示。HMM 在研究中被广泛应用,如用HMM 进行食品安全风险评估[22]、进行人脸特征标注与识别[23]等。
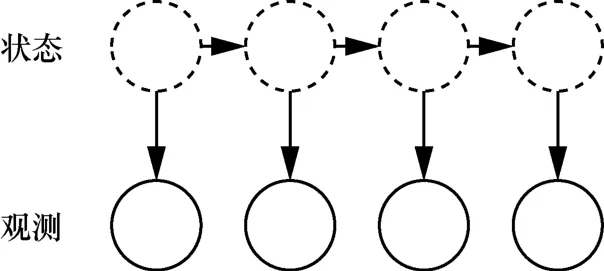
图3 HMM(1)
2.2 基于C-HMM(1)的链接预测
1) 数据聚簇
由k-means 算法的基本思想[24]可知,选到合理节点作为初始簇中心的可能性比较小,算法的复杂性也相对增加,不一定能得到理想的聚簇结果。本文了解到有学者通过聚簇分析理论提出了层次和密度聚簇分析方法的航迹关联算法[25],提高了目标数量多且相互位置较近时航迹关联的准确性;以及为了改进空间聚簇算法的效率提出了距离代价函数的概念,利用距离代价最小准则,设计了一个新的k值优化算法[26],对空间聚簇算法k-means 算法和k-中心法进行改进等。因此本文也尝试通过提高聚簇的性能,提出一种基于距离均方差最小的初始聚簇中心方法,思想如下。
一般用对象之间的距离表示相似度[27],首先根据数据集中节点的相似性矩阵(计算式如式(3)所示),得到具有最大距离的2 个节点,作为2 个聚簇的初始簇中心。
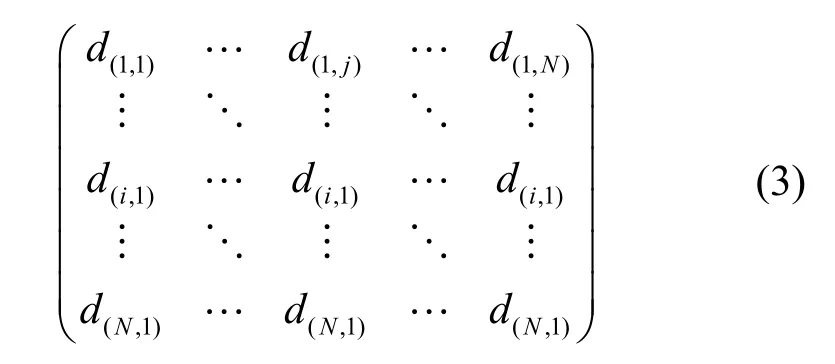
其中,d(i,j)表示节点i和节点j之间的距离,其计算式为
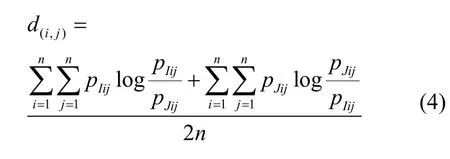
其中,pIij表示第I个节点从状态si到状态sj的转移概率。2 个节点之间的相似性程度越高,其距离值d越小。其余聚簇中心的确定方式如下:假设需要聚簇的总个数为k,已经得到的初始簇中心的个数为n,那么第n+1个待确定的簇中心与其他已得到的簇中心的距离为
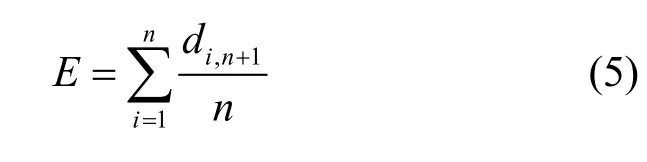
其中,di,n+1表示第n+1个簇中心与第i个簇中心之间的距离。同时,第n+1个待确定的簇中心节点需满足该簇中心到其他所有簇中心之间的距离之和最大,且和其他所有簇中心之间距离的均方差最小,也就是
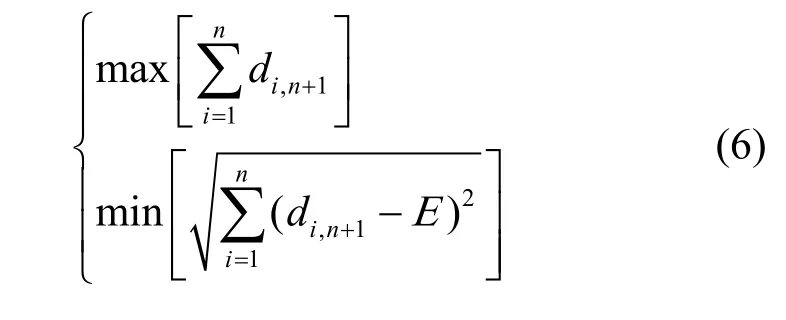
常用平方误差作为准则函数,即
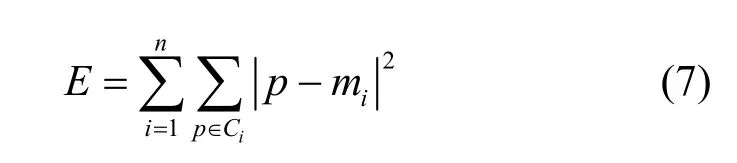
其中,Ci表示第i个聚簇,p表示Ci中的一个数据节点(p∈Ci),mi表示Ci的簇中心。
采用改进k-means 进行聚簇,聚簇算法如算法1 所示。
算法1聚簇算法
输入n 个已标记的数据训练集,聚簇数目k
输出满足函数收敛的k个聚簇
①用最大似然估计(MLE,maximum likelihood estimate)中的统计公式计算已标记的数据训练集的状态转移概率,计算训练集的初始状态概率,训练HMM;
② 用式(4)计算节点之间的距离,构造节点相似性矩阵;
③利用初始簇中心算法,初始化k个聚簇中心;
④ 将数据训练集中的节点分配给与簇中心距离最近的簇;
⑤ 计算簇的平均值,更新各簇的簇中心;
⑥ 若准则函数(式(7))未收敛,或仍有节点需要进行重新分配,则重复执行步骤④;否则结束算法,输出聚簇结果。
2) 基于聚簇一阶隐马尔可夫模型的链接预测算法
采用DBLP 数据集引入元路径的思想,抽取节点之间的关系,预测某个作者与某个会议是否存在链接关系或是否将会发生链接关系。C-HMM(1)算法主要分为以下5 个步骤。
①在保留语义信息的基础上,去除冗杂数据,提取作者、论文、会议信息。
② 提取异质网络中的作者信息,采用改进的k-means 进行聚簇分析。
③挖掘异质网络中节点之间的相关性,提取各聚簇对应的元路径。
④ 对每个聚簇分别进行训练,得到状态转移概率矩阵。
⑤ 对预测节点所在的聚簇使用 Viterbi 算法,选择概率最大的结果作为链接预测的最终结果。
C-HMM(1)算法的流程如图4 所示。
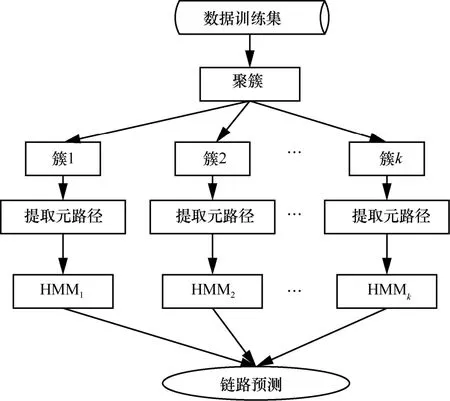
图4 C-HMM(1)算法的流程
将数据聚簇,从而得到多个簇,分别训练HMM中的3 个参数π、A、B。运用MLE 算法训练数据集并对HMM 的参数进行学习,其参数估计式为
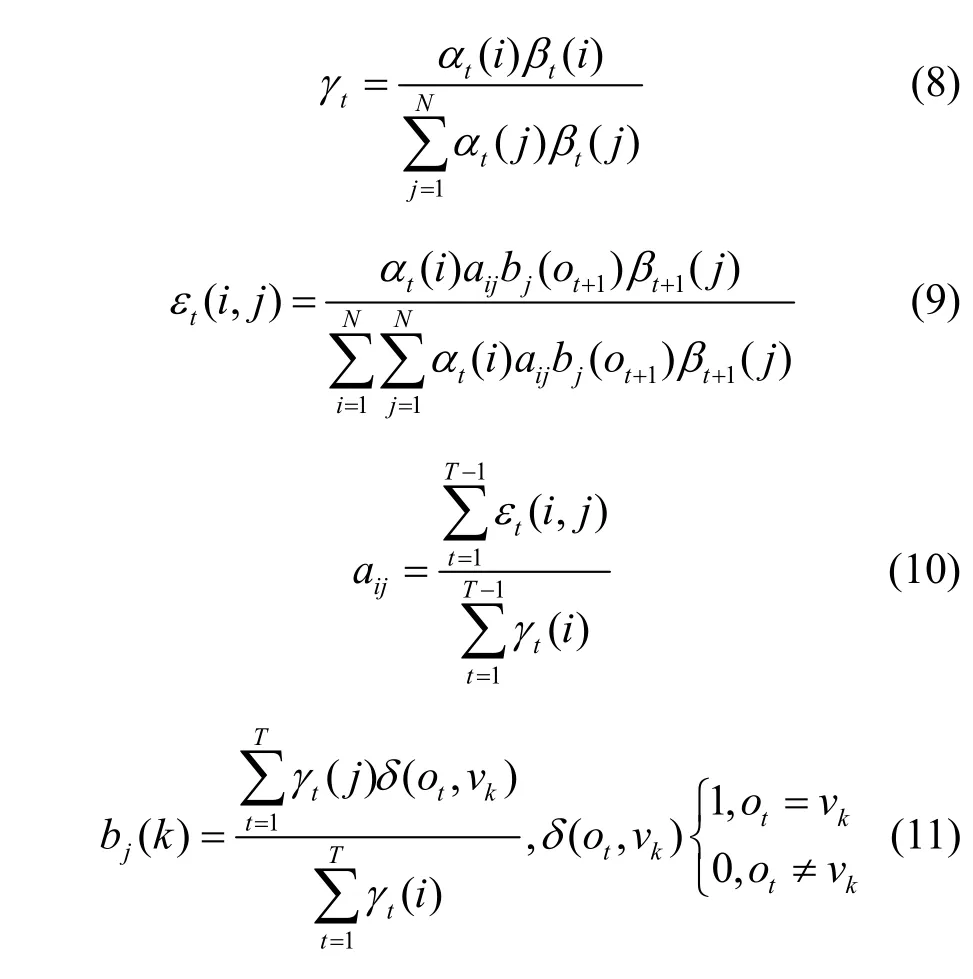
从数据集训练出HMM 的参数后,使用Viterbi算法来预测待预测节点的元路径。将 δt定义为在时刻t且状态为i的所有路径 (i1,i2,…,it)中的概率最大值,其计算方法为
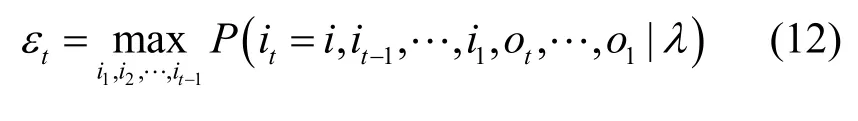
递推式为
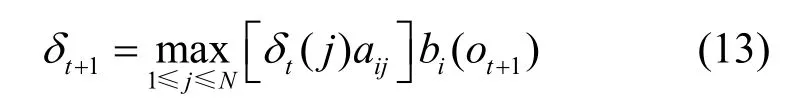
定义在时刻t且状态为i的所有路径中概率最大路径的第 t-1个节点的计算式为
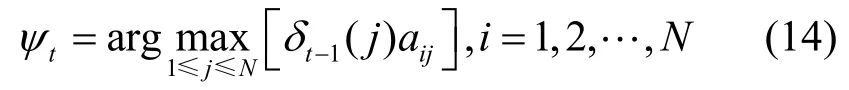
2.3 基于C-HMM(2)的链接预测
HMM(2)如图5 所示。HMM(2)增加了观测值输出的约束条件,相应地,链接预测的准确率也有较大的提高。

图5 HMM(2)
HMM(2)可以被定义为七元组(S ,O,π,A1,A2,B1,B2),七元组中S、 O、π 和C-HMM(1)中的含义一样,其他需要重点说明的介绍如下。

HMM(2)与HMM(1)一样,在链接预测中用来解决学习问题和解码问题。
C-HMM(2)算法利用数据集中的训练样本,首先用C-HMM(2)中的MLE 算法学习HMM(2)的参数,然后用C-HMM(2)中的Viterbi 算法获取链接预测的最大概率的状态序列。基于C-HMM(2)的链接预测与基于C-HMM(1)的链接预测类似:收集处理异质网络数据,对其聚簇;提取元路径;应用C-HMM(2)。
1) C-HMM(2)的MLE 算法模型
初始状态概率计算式为
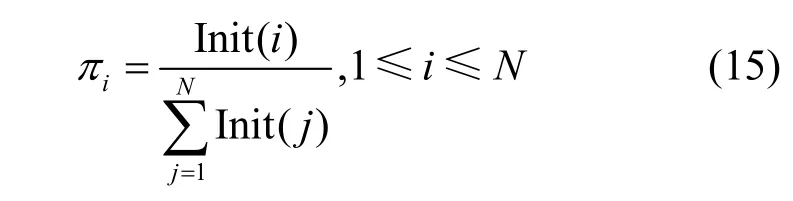
其中,Init(i)表示在数据集训练样本中初始状态si的序列数目表示在数据集训练样本中所有状态的序列数目之和。
隐含状态转移概率计算式为
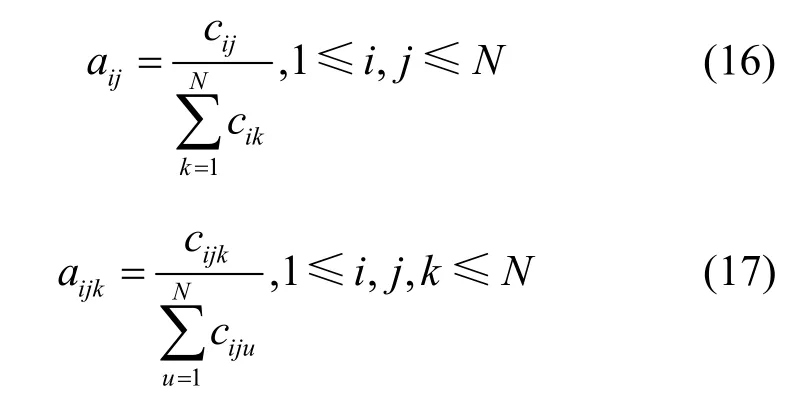
其中,cij表示数据集训练样本中,在时刻t状态为si、时刻 t+1状态转换为sj的次数;cijk表示数据集训练样本中,在时刻 t-1状态为si、时刻t状态为sj、时刻 t+1转换为状态sk的次数;表示在数据集训练样本中,在时刻 t-1状态为si、时刻t状态为sj,时刻 t+1转换到所有状态的次数之和。
观测状态转移概率计算式为
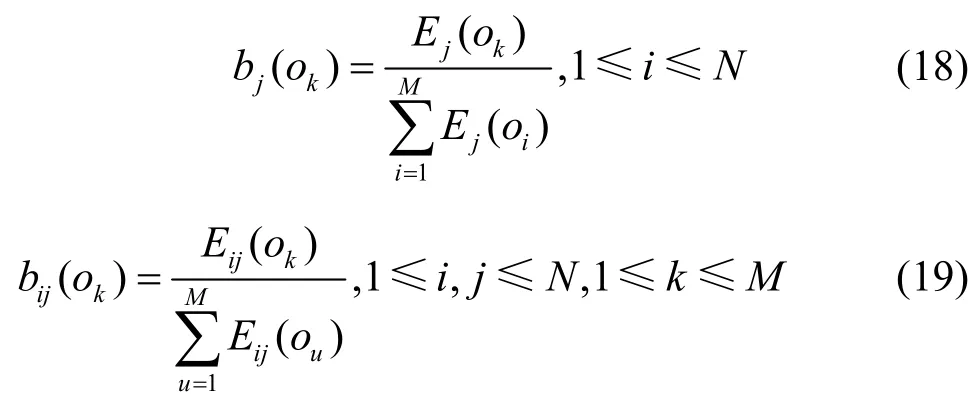
其中,Ej(ok)表示数据集训练样本中,在时刻t状态为sj时可观测状态为ok的次数表示数据集训练样本中,在时刻 t-1状态为si、时刻t状态为sj时可观测状态为ok的次数表示数据集训练样本中,在时刻 t-1状态为si、时刻t状态为sj时所有观测状态为ok的次数之和。


3 基于最大熵隐马尔可夫模型的异质网络链接预测
最大熵原理的主要思想是在只掌握知识的部分信息且是未知知识时,应该选择对已知的知识熵最大的概率分布。为了进一步提高链接预测性和准确率,在最大熵模型中加入了特征信息对链接预测中状态转移的影响,提出了ME-HMM 方法,如图6所示。ME-HMM 方法处理流程大致概括为:对异质网络数据集聚簇并提取元路径;进行最大熵处理提取特征;应用C-HMM(2)。
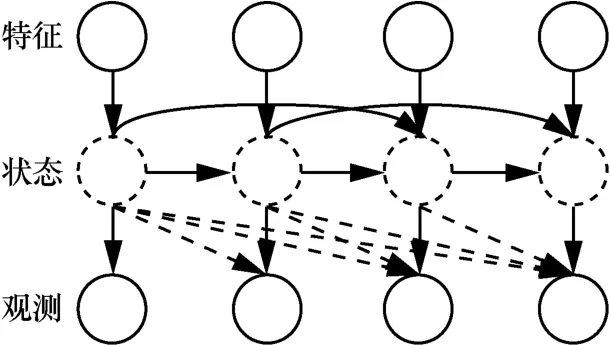
图6 ME-HMM 方法
3.1 特征-状态转移概率矩阵的训练
首先在数据集中选择合适的特征信息,考虑这些特征信息对链接预测模型状态转移的影响,将其加入链接预测模型的训练中,训练特征-状态转移概率矩阵。
1) 提取特征信息。根据本文采用的数据集,选取一些特征信息,如是否包含人名、是否都是大写字母、是否以“.”结尾、是否以“a”开头、是否以“v”开头。
如果特征信息l只影响一个状态sj,则应用

如果特征信息l同时影响状态sj和状态si,则应用

2) 计算特征-状态转移概率矩阵。当特征信息l只影响状态sj时,特征-状态转移概率矩阵为M={Mi,j},其中Mi,j是从状态i到状态j的转移概率,且满足
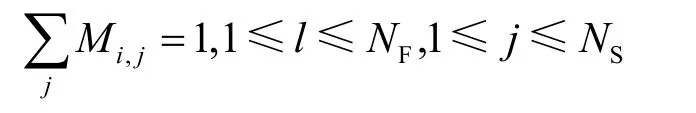
其中,NF表示特征的个数,NS表示状态的个数。
当特征信息l同时影响状态sj和si时,特征-状态转移概率矩阵为其中l,i,j
M 是从状态l到状态i、状态j的状态转移概率,且满足
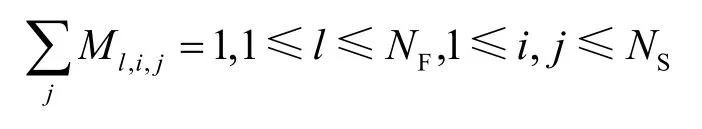
训练特征-状态转移概率矩阵的步骤如下。
①计算数据集中每个特征-状态的平均值。假设可观测状态的长度是ms,第l个特征信息、第j个状态平均值的计算式为
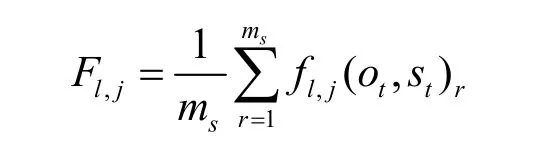
第l个特征信息、第i个状态、第j个状态平均值的计算式为
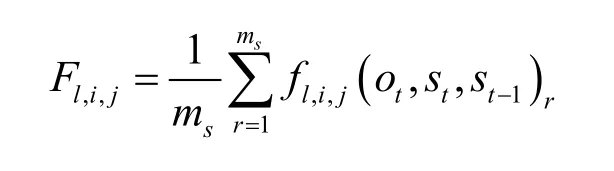
② 根据GIS 参数估计算法,得出特征-状态概率矩阵。
3.2 结合最大熵的状态转移概率
在最大熵的C-HMM(2)中,时刻 t+1的状态sk的转移概率由时刻t的状态sj、时刻 t-1的状态si,以及在时刻t得到的特征-状态转移概率共同决定。
当第l个特征信息仅影响状态sk时,状态sk的状态转移概率的计算式为
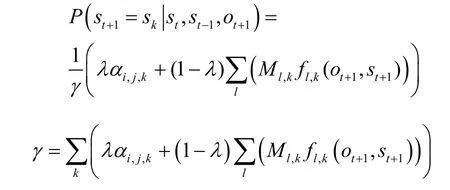
其中,αi,j,k是时刻 t-1状态为si、时刻t状态为sj时,时刻 t+1状态是sk的状态转移概率,γ 是归一化常数。
当第l个特征信息同时影响sk和si时,状态sk的状态转移概率的计算式为
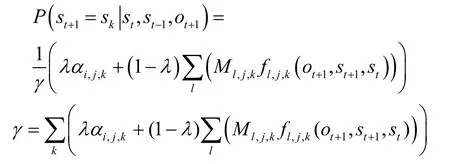
其中,λ 是调节特征-状态转移概率和状态转移概率矩阵重要性的权重。
4 实验结果与分析
4.1 数据预处理
本文所采用的DBLP 数据集为XML 格式文件且文件较大,在此选择SAX 解析方式来处理文件。DBLP 数据集按年份列出了60 000 多名作者的科研成果,包括72 902 篇论文和464 个会议。其中,每条数据中包含、、<page>、<year>、<volume>、<journal>、<ee>、<url>等信息。</p><p>数据预处理首先需要提取数据中所收录的论文,每一条记录中都包含论文的作者、标题、会议等信息。论文中涉及的作者为合作关系,同时将论文的标题信息加入相关作者的属性信息中。另外,在当前数据库中检索当前作者相关的其他论文,保证作者的文本属性完整。本文只提取论文中前3 位作者与该论文的关系。DBLP 数据预处理流程如图7所示。</p><p><img src="https://img.fx361.cc/images/2023/0118/c883f12310db030eec5b15c42d05706eb3c1b8b6.webp"/></p><p>图7 DBLP 数据预处理流程</p><p>本文在Intel i7 10750H 6 核12 线程CPU 主频为2.6 GHz 的机器上运行程序,随机抽取90%的数据集作为训练集,剩下的10%作为测试集。</p><h3>4.2 抽取元路径</h3><p>本文通过随机游走模型生成元路径来表示网络结构和节点的上下文关系,并采用skip-gram 模型生成异质网络的节点表示,提取出待预测的2 个节点之间的元路径作为候选集。同时通过调查大量基于元路径的研究和工作发现,异质网络中最常用的也是最有效的元路径方案是APVPA,表示的语义信息是两位作者在同一会议发表论文的关系。考虑到本文的实验环境,本文抽取的元路径长度是100,每个节点的游走次数是500。部分抽取的元路径如图8 所示。</p><p><img src="https://img.fx361.cc/images/2023/0118/bae39eba5470bd22811ec23f9a271c5f9b2abaa2.webp"/></p><p>图8 部分抽取的元路径</p><h3>4.3 实验评价指标</h3><p>采用计算测试集的精确度(Precision)、召回率(Recall)、F 值(F-Measure)3 种指标作为衡量本文提出的链接预测模型的指标。本文将链接预测的结果分为有链接和无链接2 种,将有链接的数据定义为正例,无链接的数据定义为负例。针对以上2 种不同情况,分别计算Precision 和Recall。总体的Precision 和Recall 分别如式(22)和式(23)所示。</p><p><img src="https://img.fx361.cc/images/2023/0118/ff6c9cb6c73e1a119c1907add414bd6255b189c3.webp"/></p><p>其中,PrecisionE和 PrecisionN分别为正例和反例的准确率,RecallE和 RecallN分别为正例和反例的召回率。精确率表示预测正确的链接数目占预测为有链接(无链接)的数目的比值;召回率又称查全率,表示预测正确的链接数目占实际存在链接(无链接)的数目的比值。采用Precision 和Recall 这2 个指标的调和平均值F-Measure 作为评估标准,其计算式为其中,β 是衡量精确度和召回率重要性的权值,本文将β 的值设为常数1。</p><p><img src="https://img.fx361.cc/images/2023/0118/ba67ff5e721a4ec323cbfad64443fd28db66865d.webp"/></p><h3>4.4 实验结果及分析</h3><p>本文选择 CN、RWR、HMM、BRLinks、MDGCN、PURP 方法来进行对比实验。首先确定聚簇的数目,以达到最佳的链接预测性能。通过多次改变聚簇数目进行实验测试,得到链接预测的总精确度与聚簇数目的关系,如图9 所示。</p><p><img src="https://img.fx361.cc/images/2023/0118/85d721effe3a59a2b48a9753cfe5f1e600d71161.webp"/></p><p>图9 链接预测的总精确度与聚簇数目的关系</p><p>从图9 中可以看出,链接预测的总精确度随着聚簇数目的增加而提高,但当聚簇数目为6 时,精确度不再有明显的提高。其原因一方面是有些聚簇训练得到的HMM 的链接预测准确率大致相同;另一方面是对于同一条元路径来说,不同模型的链接预测结果可能相同;除此之外,聚簇数目多的簇中可能包含的训练数据不多,通过这些簇得到的链接预测模型很少作为最终的链接预测结果。因此,这些新增簇对HMM 链接预测的结果影响不大。同时,本节又对不同聚簇数目下的程序运行时间做了测试,如图10 所示。</p><p><img src="https://img.fx361.cc/images/2023/0118/7f5ba7dea9ac216fd4acafc36e649b1e00fa4316.webp"/></p><p>图10 不同聚簇数目下的程序运行时间</p><p>从图10 中可以看出,聚簇数目越多,程序运行时间也就更多。图9 和图10 的实验数据表明,本文实验选择聚簇数目为6 的效果是最佳的,因此以下对比实验均采用聚簇数目为6。</p><p>1) C-HMM(1)和HMM 链接预测的实验对比</p><p>选择最佳聚簇数目6 进行C-HMM(1)和HMM这2 种方法的实验。C-HMM(1)和HMM 链接预测总精确度比较如图11 所示。</p><p><img src="https://img.fx361.cc/images/2023/0118/943631048871b0989a4cba71b1371e74a9881183.webp"/></p><p>图11 C-HMM(1)和HMM 链接预测总精确度比较</p><p>从图11 中可以看出,C-HMM(1)总精确度比单独使用HMM 精确度高。当训练元路径数为170 000 时,预测类型节点链接预测精确度比较如表1 所示,进一步说明聚簇能更有效地捕捉异质网络的结构信息,因此C-HMM(1)有更好的链接预测性能。</p><p><img src="https://img.fx361.cc/images/2023/0118/ad6f4095bcefd30ccb2026f4c8a435aa01f266b2.webp"/></p><p>表1 C-HMM(1)和HMM 对各状态链接预测精确度比较</p><p>2) C-HMM(1)和C-HMM(2)链接预测的实验对比</p><p>训练集从30 000 条开始,不断增加到170 000 条,C-HMM(1)和C-HMM(2)链接预测总精确度比较如图12 所示。</p><p><img src="https://img.fx361.cc/images/2023/0118/bc96e19cdf06580b15bd7041190b10332cb0cb02.webp"/></p><p>图12 C-HMM(1)和C-HMM(2)链接预测总精确度比较</p><p>从图12 中可以看出,选取不同数量的元路径,C-HMM(2)链接预测的总精确度都高于C-HMM(1)。随着训练数据的增加,C-HMM(2)的总精确度始终较高,这是因为随着训练数据的增加,C-HMM(2)更加优化,识别错误的能力更强。当训练数据从120 000 条增加到150 000 条时,2 种方法精确度提高不大,这可能是因为此时增加的训练集和测试集中数据的匹配度较低。</p><p>以150 000条元路径作为训练集为例,C-HMM(1)和C-HMM(2)链接预测的总精确度如表2 所示。</p><p><img src="https://img.fx361.cc/images/2023/0118/d0bae9e6bd77b3d291d13a6d39b3c7c3f90ce009.webp"/></p><p>表2 C-HMM(1)和C-HMM(2)链接预测的总精确度</p><p>从表2 中可以看出,基于C-HMM(2)的链接预测精确度高于C-HMM(1)的链接预测精确度,更进一步论证了C-HMM(2)的算法性能高于C-HMM(1)。</p><p>3) ME-CHMM 链接预测的实验对比</p><p>选取相关的特征信息,建立相关的特征匹配字典进行匹配。在判断是否包含人名特征信息时,使用从网上下载的外国人名进行匹配;对于是否都是大写字母、是否以“a”“v”开头、是否以“.”结尾的特征信息,不需要建立特征字典,在程序中可以通过逻辑判断的方式进行匹配。在实验中,进行交叉测试,取平均值,不断调整特征-状态转移概率和状态转移概率的相对重要程度λ 的值。当λ 取0.6、训练集从30 000 条增加到170 000 条时,部分链接预测方法总精确度的比较如图13 所示。</p><p><img src="https://img.fx361.cc/images/2023/0118/87dec278f6e8e5d9019bb86cebbadb3859db8559.webp"/></p><p>图13 部分链接预测方法总精确度的比较</p><p>从图13 中可以看出,随着训练数据的增加,各方法的总精确度都有不同程度的提升,其中ME-HMM 的链接预测总精确度高于其他模型,尤其是高于CN、RWR 和基准方法。C-HMM(1)和C-HMM(2)随着训练数据的增加,链接预测的总精确度有所下降,这是由于新增加的训练集与测试集匹配度不高,但是在ME-HMM 模型的预测中,这种情况并没有出现,这表明在HMM(2)中加入数据特征信息的最大熵模型对链接预测更加有效。多种链接预测方法实验比较如表3 所示。</p><p><img src="https://img.fx361.cc/images/2023/0118/f1c42b0485985ffe33dee422a83acf21cae6a08e.webp"/></p><p>表3 多种链接预测方法实验比较</p><p>从表3 中可以看出,在链接预测精确度上,C-HMM(2)比 C-HMM(1)更高;在召回率方面,C-HMM(2)没有优势,但C-HMM(2)总的F-Measure比C-HMM(1)高,这说明C-HMM(2)的链接预测性能更高。ME-HMM 在进一步提高链接预测精确度的同时,也提高了链接预测的召回率。HMM、MDGCN的精确度分别为0.829、0.830,而本文提出的方法的精确度都在0.853 以上;BRLinks、PURP 的F-Measure 的值分别为0.873、0.805,而本文提出的方法的F-Measure 都在0.903 以上,通过对比可以发现,本文提出的方法的F-Measure 至少提高了3 个百分点。由以上实验结果可知,本文提出的方法性能较为优异,其中ME-HMM 方法的性能最好。</p><h2>5 结束语</h2><p>在复杂网络中,如何更加精确地对异质网络进行链接预测一直是人们研究的热点之一,据此本文提出了通过改进k-means 算法实现基于聚簇的隐马尔可夫模型的异质网络的链接预测,并通过分析在C-HMM(2)中状态转移概率、观测值输出概率和模型历史状态之间的关系,可知链接预测的准确率有较大的提高。在此基础上,提出ME-HMM,将数据的特征信息加入链接预测中。实验表明,ME-HMM在本文中的链接预测中具有最优的性能,最大程度地提高了链接预测的准确率。但本文使用的是静态数据,没有考虑到数据的实时动态问题。但在实际生活中,数据每时每刻都在快速增长,对增量数据集的研究更符合现实网络的特征。因此,在后续的工作中,可以更深一步地对异质网络链接预测的有关课题进行研究。</p></p>
<!-- <div class="article_pdf"><a href="https://cimg.fx361.com/kkb.apk">查看pdf文档请下载app</a></div>--><div class="article_love">
<div class="title">猜你喜欢</div>
<div class="article_love_keyword"><span><a href="/tags/a/8/69e0d4ff3e202d50/1.html" target="_blank">精确度</a></span><span><a href="/tags/8/6/d6fe9e9ea24dede7/1.html" target="_blank">异质</a></span><span><a href="/tags/e/9/4c529232c5c723a9/1.html" target="_blank">概率</a></span></div>
<div class="article_love_news"><dd><a class="txt_title" href="/page/2022/0605/13882736.shtml" target="_blank" title="第6讲 “统计与概率”复习精讲">第6讲 “统计与概率”复习精讲</a><div class="rsorc"><a href="/bk/zxsslhzkb/20226.html" class="ly" title="中学生数理化·中考版(2022年6期)">中学生数理化·中考版(2022年6期)</a><span class="txt">2022-06-05 06:49:10</span></div></dd><dd><a class="txt_title" href="/page/2021/1122/13906631.shtml" target="_blank" title="第6讲 “统计与概率”复习精讲">第6讲 “统计与概率”复习精讲</a><div class="rsorc"><a href="/bk/zxsslhzkb/20216.html" class="ly" title="中学生数理化·中考版(2021年6期)">中学生数理化·中考版(2021年6期)</a><span class="txt">2021-11-22 07:52:30</span></div></dd><dd><a class="txt_title" href="/page/2021/0806/13622883.shtml" target="_blank" title="概率与统计(一)">概率与统计(一)</a><div class="rsorc"><a href="/bk/xsjznsxbk/20214.html" class="ly" title="新世纪智能(数学备考)(2021年4期)">新世纪智能(数学备考)(2021年4期)</a><span class="txt">2021-08-06 09:04:50</span></div></dd><dd><a class="txt_title" href="/page/2021/0806/13622910.shtml" target="_blank" title="概率与统计(二)">概率与统计(二)</a><div class="rsorc"><a href="/bk/xsjznsxbk/20214.html" class="ly" title="新世纪智能(数学备考)(2021年4期)">新世纪智能(数学备考)(2021年4期)</a><span class="txt">2021-08-06 09:04:50</span></div></dd><dd><a class="txt_title" href="/page/2021/0107/17743150.shtml" target="_blank" title="研究核心素养呈现特征提高复习教学精确度">研究核心素养呈现特征提高复习教学精确度</a><div class="rsorc"><a href="/bk/ynjyzxjs/202011.html" class="ly" title="云南教育·中学教师(2020年11期)">云南教育·中学教师(2020年11期)</a><span class="txt">2021-01-07 08:26:28</span></div></dd><dd><a class="txt_title" href="/page/2020/0306/13728969.shtml" target="_blank" title="“硬核”定位系统入驻兖矿集团,精确度以厘米计算">“硬核”定位系统入驻兖矿集团,精确度以厘米计算</a><div class="rsorc"><a href="/bk/sdmtkj/20201.html" class="ly" title="山东煤炭科技(2020年1期)">山东煤炭科技(2020年1期)</a><span class="txt">2020-03-06 06:43:28</span></div></dd><dd><a class="txt_title" href="/page/2015/1226/17144591.shtml" target="_blank" title="随机与异质网络共存的SIS传染病模型的定性分析">随机与异质网络共存的SIS传染病模型的定性分析</a><div class="rsorc"><a href="/bk/ynsfdxxbzrkxb/20155.html" class="ly" title="云南师范大学学报(自然科学版)(2015年5期)">云南师范大学学报(自然科学版)(2015年5期)</a><span class="txt">2015-12-26 12:46:16</span></div></dd><dd><a class="txt_title" href="/page/2015/0609/15310330.shtml" target="_blank" title="Ag2CO3/Ag2O异质p-n结光催化剂的制备及其可见光光催化性能">Ag2CO3/Ag2O异质p-n结光催化剂的制备及其可见光光催化性能</a><div class="rsorc"><a href="/bk/zymzdxxbzrkxb/20152.html" class="ly" title="中央民族大学学报(自然科学版)(2015年2期)">中央民族大学学报(自然科学版)(2015年2期)</a><span class="txt">2015-06-09 08:45:26</span></div></dd><dd><a class="txt_title" href="/page/2015/0228/19218841.shtml" target="_blank" title="MoS2/ZnO异质结的光电特性">MoS2/ZnO异质结的光电特性</a><div class="rsorc"><a href="/bk/wlsy/201510.html" class="ly" title="物理实验(2015年10期)">物理实验(2015年10期)</a><span class="txt">2015-02-28 17:36:52</span></div></dd><dd><a class="txt_title" href="/page/2013/0311/13220575.shtml" target="_blank" title="执政者应学习异质传播">执政者应学习异质传播</a><div class="rsorc"><a href="/bk/gwywc/20135.html" class="ly" title="公务员文萃(2013年5期)">公务员文萃(2013年5期)</a><span class="txt">2013-03-11 16:08:34</span></div></dd></div>
</div><div class="other_pel mt80">
<p class="fl"><a href="/bk/tongxinxb/20225.html" target="_blank"><img src="https://cimg.fx361.com/images/2023/0118/0c0b70621877fe883e523f9c3c80a84053a7fb6a.webp" alt=""></a><span class="p1"><a href="/bk/tongxinxb/" target="_blank">通信学报</a></span><span class="p2"><a href="/bk/tongxinxb/20225.html" target="_blank">2022年5期</a></span></p>
<dl class="fl"><dt>通信学报的其它文章</dt><dd><a href="/page/2022/0607/15124046.shtml" title="基于推土机距离的证据冲突强度量方法">基于推土机距离的证据冲突强度量方法</a></dd><dd><a href="/page/2022/0607/15123962.shtml" title="基于深度学习的光学遥感图像目标检测研究进展">基于深度学习的光学遥感图像目标检测研究进展</a></dd><dd><a href="/page/2022/0607/15123934.shtml" title="低轨巨型星座网络:组网技术与研究现状">低轨巨型星座网络:组网技术与研究现状</a></dd><dd><a href="/page/2022/0607/15123913.shtml" title="高速移动环境下基于RM-Net 的大规模MIMO CSI 反馈算法">高速移动环境下基于RM-Net 的大规模MIMO CSI 反馈算法</a></dd><dd><a href="/page/2022/0607/15123617.shtml" title="基于改进PSO 的铁路监测线性无线传感器网络路由算法">基于改进PSO 的铁路监测线性无线传感器网络路由算法</a></dd><dd><a href="/page/2022/0607/15123086.shtml" title="基于云边协同的无证书多用户多关键字密文检索方案">基于云边协同的无证书多用户多关键字密文检索方案</a></dd></dl>
</div></div>
</div>
</div>
<div class="sidebarR">
<!-- tab选项卡 -->
<div class="tab01 mb20"><div class="tabArrow"></div><div class="tabItem"><div class="tabTit"><a href="#">杂志排行</a></div>
<div class="tabCont"><ol><li><p class="row01"><span class="topNum">1</span><a href="/bk/sdjy/202410.html" class="row01a">《师道·教研》</a><span class="row01_fr"><a href="/bk/sdjy/202410.html">2024年10期</a></span></p></li><li><p class="row01"><span class="topNum">2</span><a href="/bk/swyzhsby/202411.html" class="row01a">《思维与智慧·上半月》</a><span class="row01_fr"><a href="/bk/swyzhsby/202411.html">2024年11期</a></span></p></li><li><p class="row01"><span class="topNum">3</span><a href="/bk/xdgyjjhxxh/20242.html" class="row01a">《现代工业经济和信息化》</a><span class="row01_fr"><a href="/bk/xdgyjjhxxh/20242.html">2024年2期</a></span></p></li><li><p class="row01"><span class="topNum">4</span><a href="/bk/wxxsyb/202410.html" class="row01a">《微型小说月报》</a><span class="row01_fr"><a href="/bk/wxxsyb/202410.html">2024年10期</a></span></p></li><li><p class="row01"><span class="topNum">5</span><a href="/bk/gywsw/20241.html" class="row01a">《工业微生物》</a><span class="row01_fr"><a href="/bk/gywsw/20241.html">2024年1期</a></span></p></li><li><p class="row01"><span class="topNum">6</span><a href="/bk/xl/20249.html" class="row01a">《雪莲》</a><span class="row01_fr"><a href="/bk/xl/20249.html">2024年9期</a></span></p></li><li><p class="row01"><span class="topNum">7</span><a href="/bk/sjbl/202421.html" class="row01a">《世界博览》</a><span class="row01_fr"><a href="/bk/sjbl/202421.html">2024年21期</a></span></p></li><li><p class="row01"><span class="topNum">8</span><a href="/bk/zxqyglykj/20246.html" class="row01a">《中小企业管理与科技》</a><span class="row01_fr"><a href="/bk/zxqyglykj/20246.html">2024年6期</a></span></p></li><li><p class="row01"><span class="topNum">9</span><a href="/bk/xdsp/20244.html" class="row01a">《现代食品》</a><span class="row01_fr"><a href="/bk/xdsp/20244.html">2024年4期</a></span></p></li><li><p class="row01"><span class="topNum">10</span><a href="/bk/wszyjy/202410.html" class="row01a">《卫生职业教育》</a><span class="row01_fr"><a href="/bk/wszyjy/202410.html">2024年10期</a></span></p></li></ol> </div></div>
</div>
</div>
<div class="clr"></div>
</div>
</div>
<!--div class="advertisement">
</div-->
<div class="footer">
<p><a href="/aboutus/index.html">关于参考网</a></p>
</div>
<script>
if ('serviceWorker' in navigator) {
window.onload = function () {
navigator.serviceWorker.register('/sw.js');
};
}
</script>
<script type="text/javascript" src="https://s1.pstatp.com/cdn/expire-1-M/jquery/3.4.0/jquery.min.js"></script>
<script type="text/javascript" src="https://s1.pstatp.com/cdn/expire-1-M/sticky-kit/1.1.3/sticky-kit.min.js"></script>
<script type="text/javascript" src="https://s1.pstatp.com/cdn/expire-1-M/jquery.lazyload/1.9.1/jquery.lazyload.js"></script>
<script type="text/javascript">
document.write('<script src="https://img.fx361.cc/cdn/w/index_cc.js"><\/script>');
</script>
</body>
</html>