基于推土机距离的证据冲突强度量方法

王欣，付威

（1.黑龙江大学自动化系，黑龙江 哈尔滨 150080；2.黑龙江省信息融合估计与检测重点实验室，黑龙江 哈尔滨 150080）

0 引言

近年来，多传感器信息融合技术受到了极大的关注，并被广泛应用于目标检测[1]、医疗[2-3]和金融[4]等领域。在信息融合领域中，为了有效地整合来自不同传感器的信息，选择一种合适的融合策略是至关重要的。作为多传感器信息融合技术的重要方法之一，D-S（Dempster-Shafer）证据理论具有显著的优势，它既能有效地表达不确定信息，又能在没有先验信息的情况下融合证据[5-6]。因此，D-S 证据理论在风险评估[7]、模式识别[8]和故障诊断[9]等领域得到了广泛的应用。

在实际应用中，信息种类的多样性、环境的复杂性和传感器的局限性使信息源一般具有较强的不确定性和高冲突性[10]，在使用D-S 证据理论融合高冲突证据时，往往会出现反直观的结果，如Zadeh[11]提出的0 信任和1 信任等反直观结果。针对这一问题，许多研究者提出了不同的冲突度量方法，大致可以分为两类：一类是在度量证据间的冲突程度前对证据进行预修正，另一类是在原始证据的基础上直接度量证据间的冲突程度。

对证据进行预修正的方法也可分为两类，一类是通过构造关系矩阵来修正证据，如宋亚飞等[12]利用关系矩阵对证据进行修正，然后将测得的修正后的证据之间的夹角余弦值作为证据间的冲突程度；孙贵东等[13]基于核关系矩阵对证据进行修正，然后提出了一种证据冲突度量方法。另一类是基于Pignistic概率转换（PPT,Pignistic probability transform）的方法，如Liu[14]定义了Pignistic 概率距离来度量由PPT修正后的证据间的冲突程度；郭兴林等[15]提出了一种基于PPT 和奇异值分解的证据冲突度量方法；Cai等[16]将PPT 推广为Pignistic 信任转换（PBT,Pignistic belief transform），以此将非单子集焦元的信任分配给多个集合，并提出了一种新的证据冲突度量方法，但是这种方法的复杂度较高，不便于实际应用。

度量未修正证据间的冲突程度主要是通过计算证据间的距离、熵或相关系数来实现的。Jousselme 等[17]提出将证据间的Jousselme 距离作为证据间的冲突度量。邓勇等[18]引入随机变量的偏熵和关联熵，将证据间的关联系数作为证据间的冲突度量。Xiao[19-20]提出了BJS（belief Jensen-Shannon）散度和RB（reinforced belief）散度函数，并将其测出的证据间的广义距离作为证据间的冲突程度。李军伟等[21]根据最大最小法定义了新的相关系数，并提出了一种基于Einstein 算子的冲突度量方法。Jiang[22]提出一种考虑焦元之间的不相交性和差异性的相关系数，以此来度量证据间的冲突程度。

尽管上述方法都可以度量证据间的冲突程度，但也存在一些不足。若使用第一类方法，即选择对证据进行预修正，则修正后的基本概率指派（BPA,basic probability assignment）将不再满足归一性，而且很难最大限度地保留原始信息的不确定性。而第二类方法要求不同证据的焦元数量完全相同，如果焦元数量不同，那么需要补齐焦元。上述问题均会在不同程度上影响最终的合成结果。

鉴于以上原因，本文在文献[12,20]的基础上提出了证据冲突强度量函数（ECSMF,evidence conflict strong measurement function）的期望特征，并用实例说明了已有证据冲突度量方法的不足。

根据ECSMF 的期望特征的要求，本文提出了一种基于推土机距离（EMD,earth mover’s distance）的证据冲突度量方法，即信任推土机距离（BEMD,belief earth mover’s distance）。推土机距离又叫作Wasserstein 距离，它最初是为了解决运输问题提出的，后来由Rubner 等[23]提出作为一种图像检索方法而得到了广泛的应用[24-25]。本文提出的信任推土机距离方法，不仅满足ECSMF 的所有期望特征，而且可以将单元素之间的距离概念自然地扩展到元素集或分布之间的距离概念，进而有效地度量证据间的冲突程度。

本文做了如下创新性工作：1) 提出了ECSMF的期望特征；2) 提出了信任推土机距离方法，理论和实验证明了该方法满足ECSMF 的所有期望特征；3) 提出的信任推土机距离方法不需要对证据进行预修正，也不要求不同证据的焦元完全相同，可以直接计算含有复合元素的证据之间的冲突，从而避免了高维矩阵运算，减小了计算负担，理论和实验证明了该方法的有效性。

近些年，随着什寒村旅游开发项目的推进，在国内已经形成一定的知名度，有不少游客在网上看到什寒村的宣传而到什寒来旅游，但是没找到什寒村的官网，没有具体的引导路线图，游客只能通过沿路询问找到什寒村。从旅游营销的角度来看，仍然没有建立起有效的宣传与推广机制，宣传效果不理想。

1 证据冲突强度量函数的期望特征

定义1识别框架。在D-S 证据理论中，假设是一个两两互斥又可穷举元素的完备集合，则称Θ 为识别框架。其中，θi是识别框架Θ 中的一个单子集命题，N是单子集命题的个数。

定义2BPA 函数。设Θ 为识别框架，则Θ 中的所有单子集命题组成的集合称为Θ 的幂集，记为2Θ。假设任意命题A∈2Θ，若映射m满足

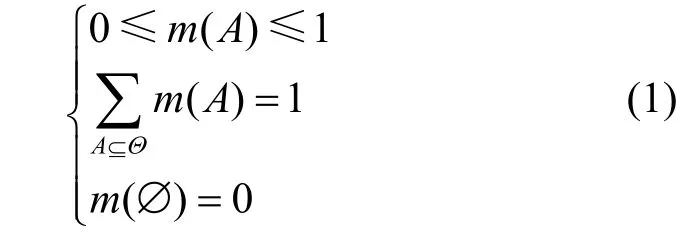
则称m为识别框架Θ 上的BPA 函数或质量函数，其中 m( A) 为A的BPA 或质量，表示对命题A的基本信度。当 m( A) ＞ 0时，则称子集A为一个焦元，所有焦元的并集称为核，记作 κ(m)。

在对药品加成政策全面取消后，医院主要收入来源减少，虽然医院及时进行了调整，增加手术等各方面的服务费用，但为了不对消费者造成过重负担，又不能过度进行加价，这就造成医院在收入方面损失严重，为弥补这方面的损失，国家出台相应政策，对医院加大补贴力度。由于各地区经济水平不尽相同，这就造成了一些地区的补贴远远达不到医院正常运转所需要的标准，导致医院必须自行解决一部分财政方面的问题，只能对各种医疗服务收费进行处理，加大了医疗患者的负担，虽然在取消药品加成的影响下，对服务进行收费是一种合理的解决办法，但不合理的抬高价格就会造成看病成本低，但实际消费高的情况的产生，这也是国家不希望看到的。

证据冲突的本质在于不同证据对相同命题的支持度存在差异，如果不同证据对同一命题的支持度接近，那么它们之间的冲突就很小；反之，则说明2 个证据的冲突较大。文献[12]提出了证据相关系数法来测量冲突，给出了相关系数满足对称性、规范性、同一性和不反直观性。文献[20]提出了基于RB 散度来测量冲突，给出了其对称性、规范性、同一性和三角不等式的性质。综合文献[12,20]所提方法的性质，下面给出证据冲突强度量函数应该满足的数学特征。

纵观全县之地层，出露部分主要包含了白云岩、石灰岩、钙质页岩、泥灰岩、白云质灰岩等类型，石材质地较软，便于开采加工。独特的自然环境孕育了当地极具地域特色的民居，尤以县境东部的石板房最为独特。

定义3ECSMF 的期望特征。在同一识别框架Θ 下，存在2 个证据m1和m2，则两者的冲突强度量函数 f (m1,m2)的期望特征如下。

2 基本概述

2.1 现有冲突度量方法存在的问题

2.1.1 D-S 组合规则

纵观当前林政资源管理中生态建设的现状来看，虽然较以往取得一定的成效，但是其中仍旧存在的一定不足之处，所呈现的效果并不十分如人意。具体来说，林政资源管理中生态建设存在的问题具体表现在以下几个方面：

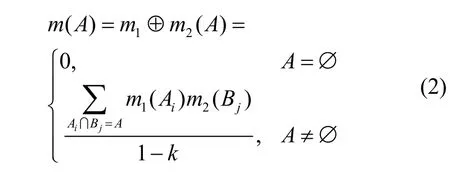
其中，k为度量冲突的冲突因子，计算式为

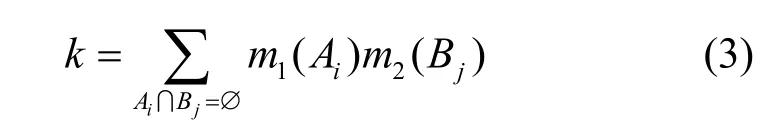
事实上，冲突因子k不能很好地反映证据之间的冲突程度，下面通过例1 来说明这一问题。

2.1.3Jousselme 冲突度量

例1假设在识别框架 { A, B ,C}

定义10BEMD。假设在完备的识别框架Θ 下存在如下2 个证据

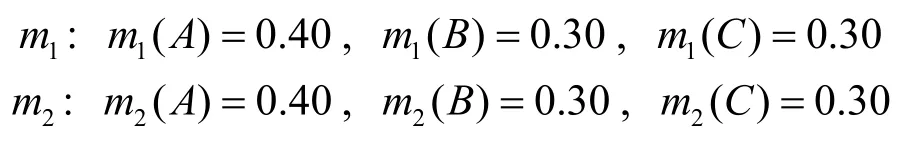
根据式(3)计算证据m1和m2之间的冲突程度，则有k=0.66，即表明2 个证据存在一定的冲突。然而证据m1和m2是完全相同的，因此，冲突因子k不能有效地度量证据间的冲突程度。这表明冲突因子k不满足ECSMF 的期望特征的同一性。

儿童贫血是临床常见疾病,据报道中国5岁以下儿童贫血率为12.6%,引起贫血的主要因素是:膳食结构、生活习惯、遗传因素,主要类型为:地中海贫血与缺铁性贫血。临床症状主要为食欲不振、肝脾肿大、皮肤黏膜苍白等。[1]并且贫血可影响到患儿的生长发育、免疫发育、智力与心理的发展。文山地区属于地中海高发地区,但是地中海贫血与缺铁性贫血的治疗方法也不尽相同,两者常规检查结果相似性较高,诊断鉴别具有一定难度,在实际过程中,目前以血液检验为主要手段。因此,本文旨在探讨血液检验应用于小儿贫血中的鉴别意义。

2.1.2Pignistic 冲突度量

定义5Pignistic 冲突度量[14]。假设识别框架Θ 中的2 个证据分别为m1和m2，则证据间的Pignistic 概率距离为

其中，BetPmi为mi的Pignistic 概率转换，即

在房屋建筑施工期间开始广泛使用太阳能技术，其可以转化为热能与电能。太阳能电池发电系统可以将太阳能转化为电能，并有效储存，满足居民的日常需求。太阳能具备清洁、无污染的特征，且相关设备也便于安装与维修。风能具备清洁、可循环利用以及环保等功能，且风力发电设备也可以将风能转化为电能，并有效储存，从而达到预期的节能效果。地源热泵技术可以有效吸收地面表层中储存的能量，有效调节建筑物的温度。夏季大地会带走多余的热量，且冬季建筑物也不会太冷，降低了能源的使用量。

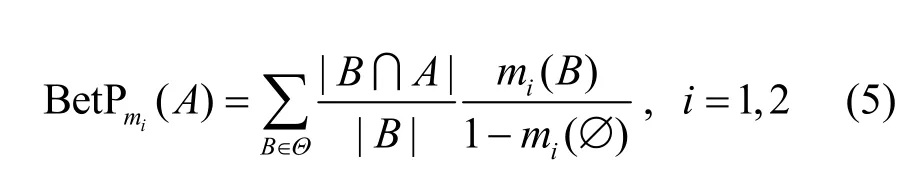
例 2假设在识别框架 Θ={ A, B ,C ,D, E ,F}下，存在2 个证据m1和m2，它们的BPA 分别为

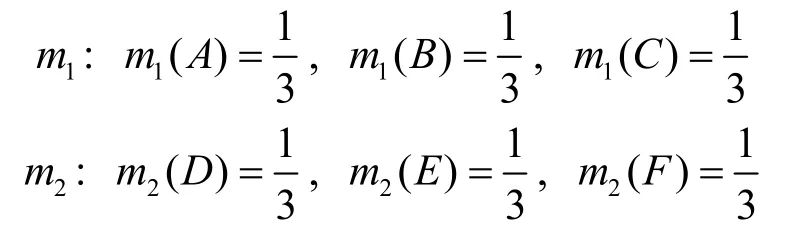
在我国相当长的时间里一直处于应试教育的大环境下，如何提高学生的考试成绩就是整个教学工作的中心.这样的教育体制在近些年来越来越暴露其出现的问题，高分低能日益显现.以高中的数学教学为例，教师只是一味地去灌输，去告诉学生解题的过程和答案，如何才能在高考的数学中获得高分，而却完全忽视对于学生的个人核心素养的培养，并没有从根本上调动学生的积极性，学生缺乏学习数学的主动性和探索知识的创造性.同时，在高中的数学课堂上，学生处于听课状态的时间较长，而真正动手练习的机会较少，更不用说小组合作探究与自我总结反思更被忽略了.如果长此下去，势必会严重地影响学生的核心素养的提高，甚至会影响国家和民族的未来

定义6假设在包含N个单子集命题的识别框架Θ 下，证据m的BPA 的向量形式为

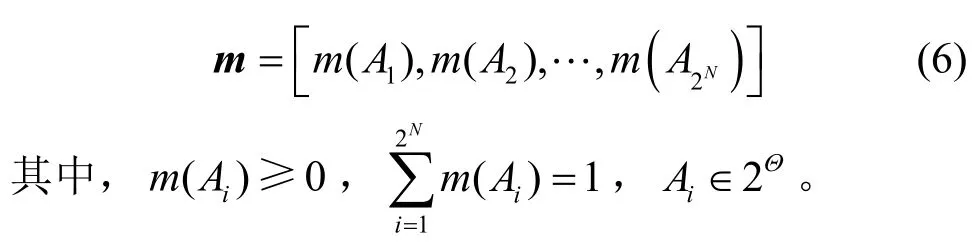
定义7Jousselme 冲突度量[17]。假设识别框架Θ 下的2 个证据为m1和m2，相应的向量形式为m1和m2，则证据间的Jousselme 证据距离定义为

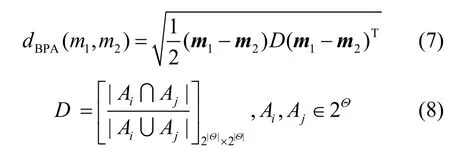
其中，| Θ |表示识别框架的基数，即识别框架所包含元素的个数；Ai和Aj分别表示证据m1和m2的焦元；上标T表示向量的转置。

科学合理的建筑规划和形态设计能够适应恶劣的气候环境，它包括建筑物整体容积的确定、建筑物的形状和建筑形式的组合、建筑物的日照和朝向。譬如，阳光和方向的选择原则是获得充足的阳光，避免冬天流通的强风，在夏季利用自然通风来防止太阳辐射。同时，建筑受社会历史条件、历史条件、地理条件、城市规划、道路、环境等因素的制约，建筑物楼面的朝向和设计应考虑多种影响因素。

例3仍以例2 为例，由式(7)和式(8)可得因此该方法也不满足互斥性。

2.1.4 BJS 散度冲突度量

定义8BJS（belief Jensen-Shannon）散度冲突度量[19]。假设识别框架Θ中的2 个证据为m1和m2，Ai为m1或m2的焦元，则m1和m2的BJS 散度冲突度量为

定义4D-S 组合规则。假设识别框架Θ 下的2 个证据为m1和m2，其相应的焦元分别为Ai和Bj，设k＜ 1，则Dempster 组合规则（也称为2 个证据的正交和）为

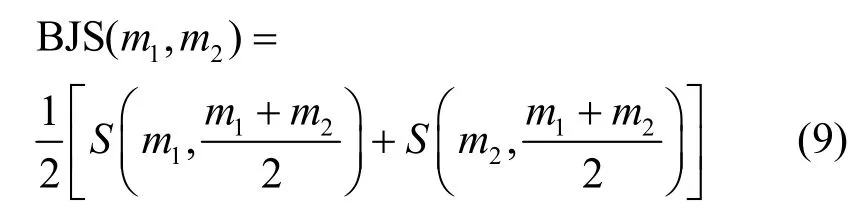
其中，S(m1,m2)是Kullback-Leibler 散度，计算式为

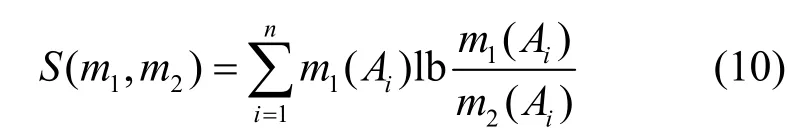
1.4 统计学方法 采用SPSS 20.0统计软件进行数据处理。计量资料以x±s表示，采用t检验；计数资料以百分比表示，等级资料组间比较采用秩和检验。以P<0.05为差异有统计学意义。

2.2 推土机距离

推土机距离[23]是一种通用且灵活的度量方法，它最初被设计用来计算运输问题中从一个分配点到另一个分配点的最低成本。后来，Rubner 等[23]提出将EMD 用于图像检索，测量两组带权元素或分布之间的距离。

定义9推土机距离。假设有两组图像的数据，第一组数据含有α 个特征，其中pi表示P中的第i个特征，ωpi表示pi的权重；第二组数据含有β 个特征，其中qj表示Q中的第j个特征表示qj的权重。则两组离散数据之间的EMD 为

本文数据来源于出租车一体化终端，利用北斗高精度定位和车载诊断(OBD)系统接口读取车辆实时位置、时间、车速、油耗、累计里程、发动机转速等信息，采样频率为1 Hz，采样车型为现代伊兰特. 采集设备如图1所示，出租车数据格式如表1所示.

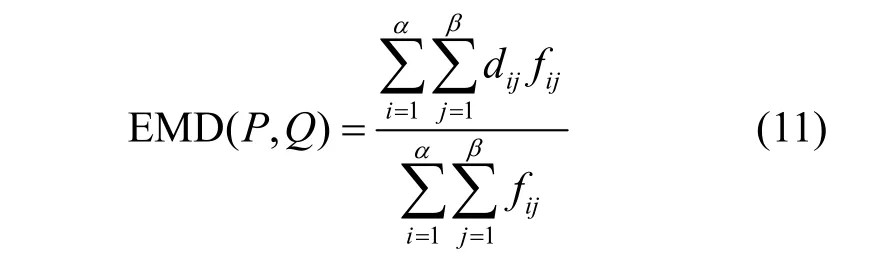
其中，dij表示随机变量pi到qj之间的距离，fij表示由 ωpi到ωqj的最小转移量，它们受到如下约束

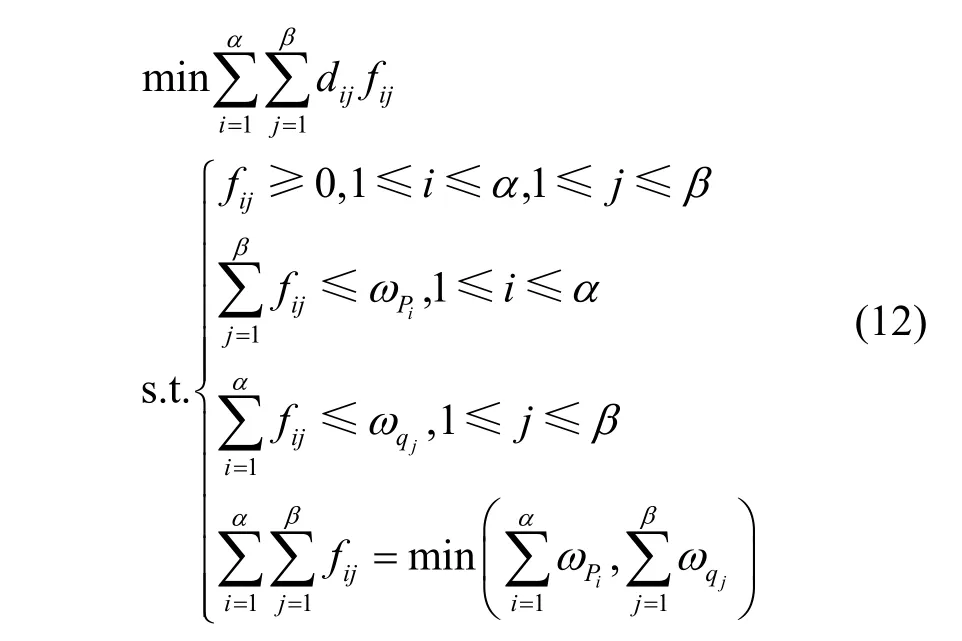
由式(12)可知，转移过程是由P转移到Q的，P中所有特征可以转移的量不超过它们本身的权重，Q中每个特征接收的量不超过相应特征的权重，两组数据可以具有不同的总权重，EMD 以较小的总权重作为归一化因子。

3 信任推土机距离

3.1 信任推土机距离的定义

针对已有的冲突度量方法不能很好地度量证据间的冲突程度的情况，本文提出了一种基于EMD 的证据冲突度量方法，即信任推土机距离，该方法对冲突程度的测量满足ECSMF 的所有期望特征，能够正确表征证据间的冲突大小，是一种有效的证据冲突强度量方法。

Θ= 下，存在如下2 个证据m1和m2。

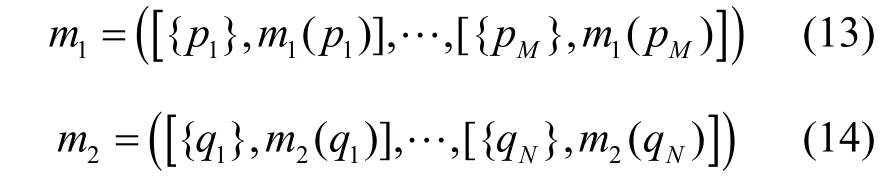
在BEMD 算法中，最耗时的计算就是求解式(17)的最优解，式(17)是一个线性规划问题，即在式(17)的条件下使最小，这可以借助MATLAB的linprog 函数求解vij，在求解BEMD 时可使用内点法，内点法的计算复杂度为 O (N3log N)[23]，其中N代表证据中焦元的数量[23]。通过生成焦元数量从1 到1 000 的证据，测试BEMD 的时间性能，并记录计算BEMD 时的CPU 耗时，结果如图1 所示。此实验环境中使用的电脑处理器为Intel(R) Core(TM) i5-9400F CPU @ 2.90 GHz，软件为MATLAB 2019a，图1 与内点法的复杂度基本一致，说明了其正确性。

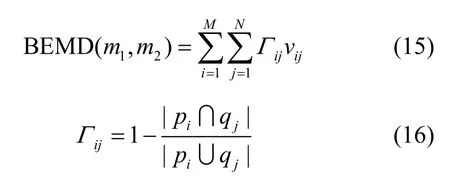
其中，Γij是Jaccard 集合距离，表示从焦元pi到焦元qj的距离；vij由式(17)中的优化问题解出

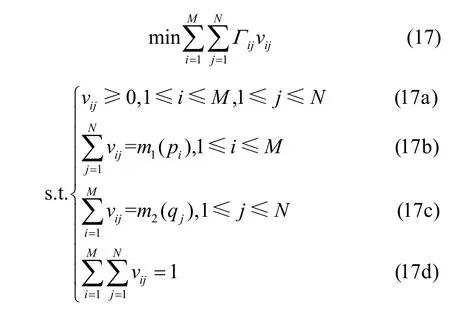
3.2 信任推土机距离的算法复杂度分析

则证据间的BEMD 为

例4假设在识别框架Θ={ A, B ,C}下，3 个证据m1、m2和m3的BPA 分别为

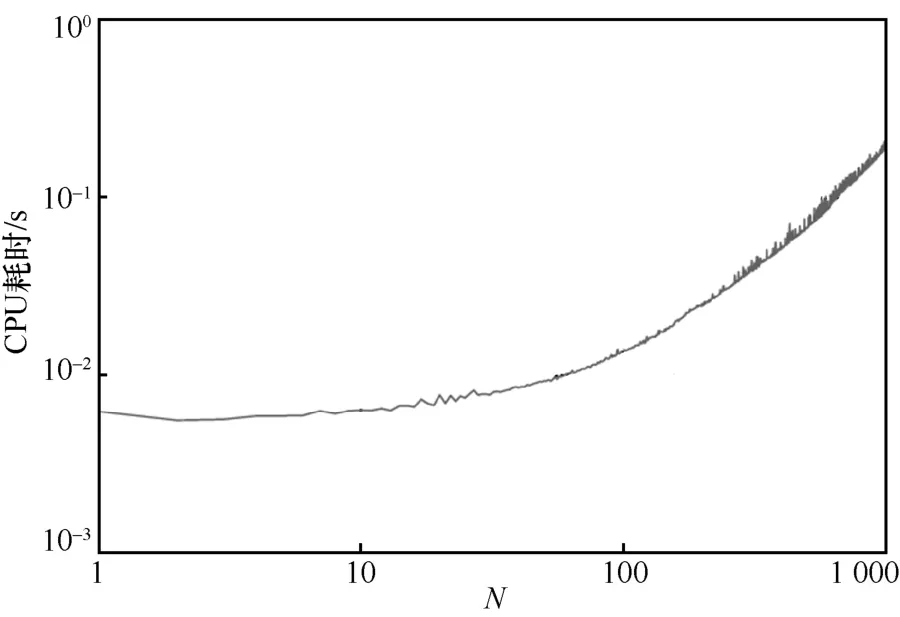
图1 改变证据焦元数量时计算BEMD 的时间双对数曲线

3.3 信任推土机距离的性质

定理1假设在完备的识别框架Θ 下有2 个证据m1和m2，其焦元分别为p1,p2,…,pM和q1,q2,…,qN，则信任推土机距离 BEMD(m1,m2)是证据m1和m2的ECSMF，即满足定义3 中ECSMF 的所有期望特征。

这表明 BEMD(m1,m2)满足三角不等式。

6) 不反直观性

甲洛洛深深地吸了一口烟，好半天才跟一声长长的叹息吐出烟雾：哎——都怪我多事，我愧对大家对我的敬重！潘美丽剜着甲洛洛：愧对管个屁用，那么多东西都拿哪儿去了？拿你的脑袋都赔不起。西西的语气里明显地带着挑衅：什么东西比脑袋还管钱？我可从来没见识过，你今天说来听听。这时大家才注意到西西脸色发紫，好像随时都会扑上去咬一口。

不反直观性需要通过实例进行验证。为了验证当证据变化时，BEMD 的变化趋势与直观分析一致，下面采用文献[17]中的例子来说明BEMD 满足特征6)，同时与文献[12,14,16-18,20]的冲突度量方法进行对比分析。

例5假设识别框架Θ={1,2,3,…,20}中有2 个证据m1和m2，每个证据的BPA 为

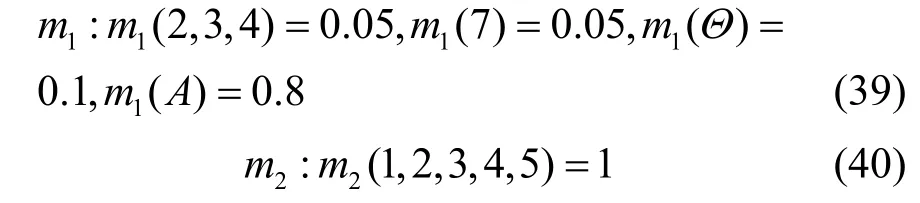
不同冲突度量方法的比较如表1 所示，各证据冲突度量随| A |变化的趋势如图2 所示。

丰田产业车辆（上海）有限公司是丰田叉车在中国的总经销商，由丰田自动织机2003年投资成立。丰田叉车已在中国拥有包括叉车生产基地、销售和服务中心在内的一套完整的运营体系，向中国用户提供全方面的服务。2007年随着公司正式启动BT产品的销售，丰田叉车将其旗下的三大品牌全部带到了中国，让中国的叉车用户也能体验到一个渠道三个品牌（Toyota、BT和Raymond）的一站式全方位物流服务。

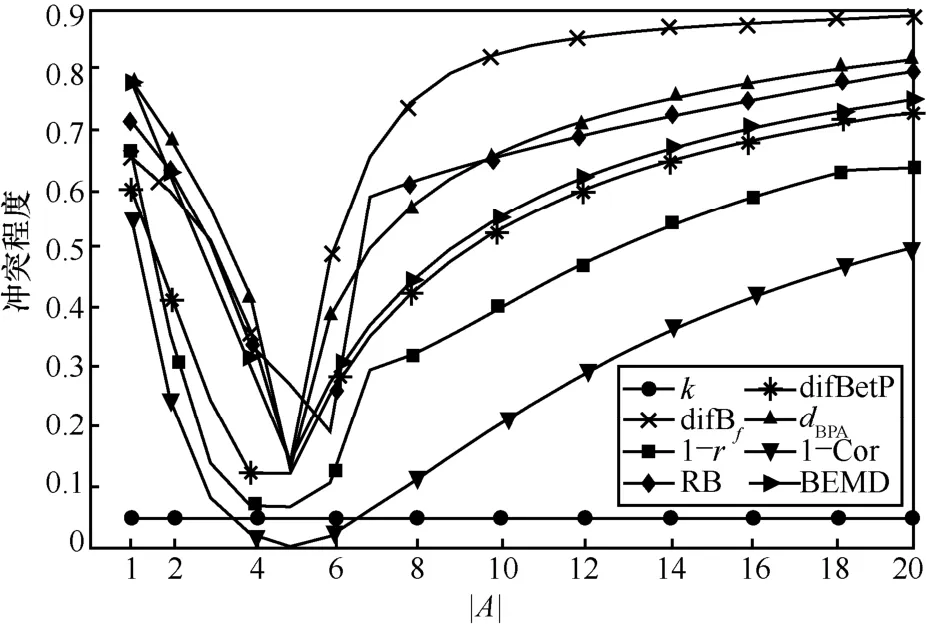
图2 各证据冲突度量随| A |变化的趋势

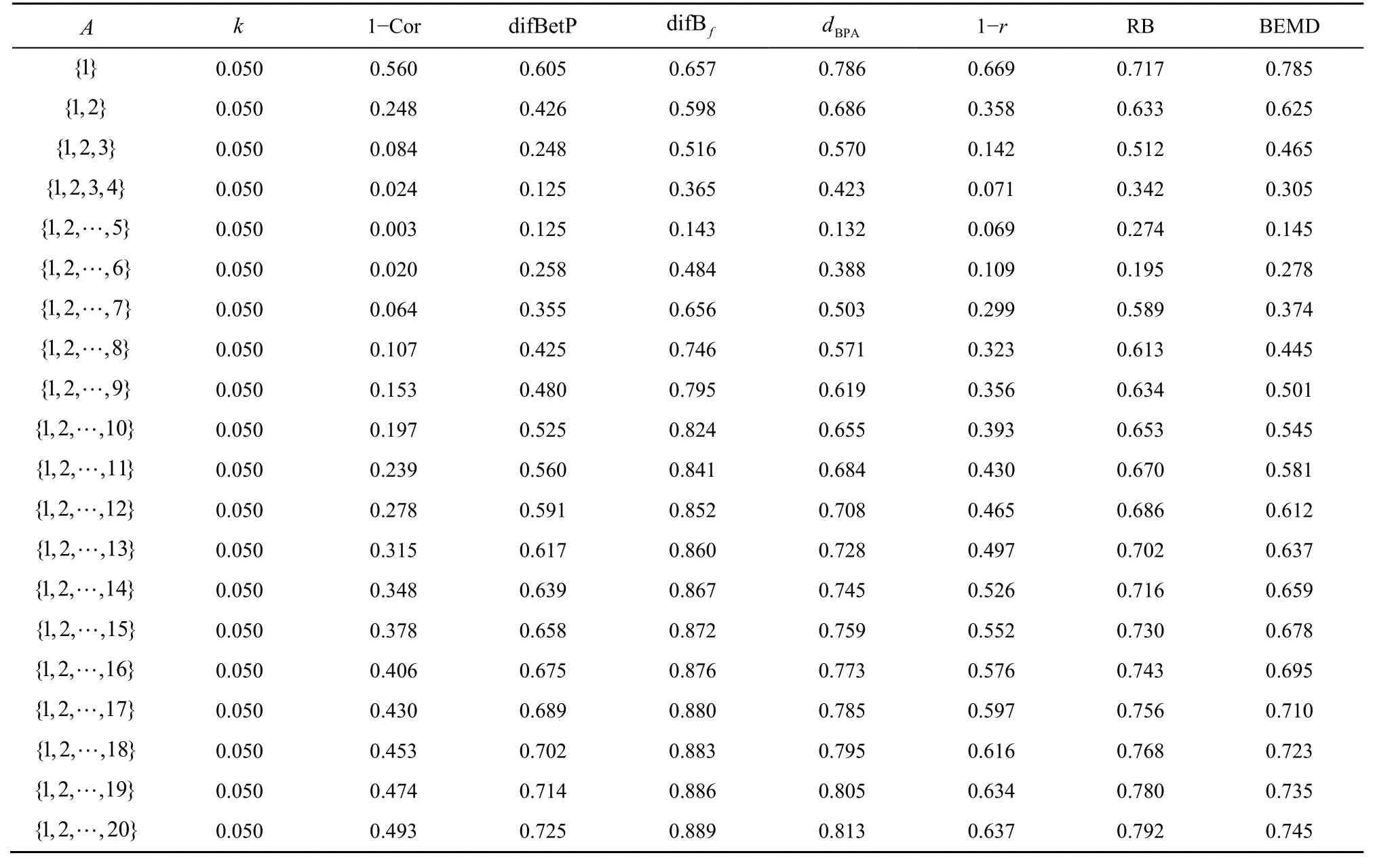
表1 不同冲突度量方法的比较

由式(39)和式(40)可知，证据m1主要支持A，证据m2完全支持{1,2,3,4,5}，而从表1 和图2 可知，随着A的变化，多数的证据冲突度量曲线整体呈先减小后增大的变化趋势，而冲突因子k的值一直为 0.05，这显然是反直观的，并且，当A={1,2,3,4,5}时，由直观分析可知证据m1与m2的冲突最小，而RB 散度[20]在 A={1,2,3,4,5,6}时的冲突度量达到最小，这显然也是与直观相悖的。在本例中，因为{1}与{1,2,…,5}的Jaccard 距离为而{1,2,…,20}与{1,2,…,5}的Jaccard 距离为所以A={1}时证据间的冲突程度应比A={1,2,…,20}时证据间的冲突程度更高，冲突曲线应呈现出左高右低的趋势。在这些冲突度量方法中，只有1 -r、1 -Cor和BEMD 的证据冲突度量曲线符合这种趋势。除此以外，与1 -r相比，BEMD 的证据冲突度量曲线较平滑，可以更精确地描述证据之间的冲突。而与1 -Cor相比，BEMD 的证据冲突度量结果更合理。以A={1,2,3,4,5}为 例，BEMD(m1,m2)=0.145，而1 -Cor(m1,m2)=0.03，这说明证据相关系数认为证据m1和m2趋近于完全相同，但是证据m1中仍含有其他命题，并且这些命题的质量不能忽略不计，这表明证据m1和m2之间仍然存在一定的冲突，BEMD 相比于证据相关系数可以更合理地度量出与直观分析相符的结果。上述分析表明，本文提出的BEMD 具有良好的性能，当证据中存在一些非单子集命题时仍可以灵敏准确地反映证据之间的冲突程度，并且度量的冲突结果与直观分析相一致。本例验证了所提出的BEMD 满足ECSMF 的不反直观性。

4 算例分析

本节将通过实验来进一步验证BEMD 满足ECSMF 的所有期望特征，并通过与已有文献方法的比较分析阐述它的有效性。

例6假设识别框架Θ={ A, B}中有2 个证据m1和m2，它们的BPA 分别为

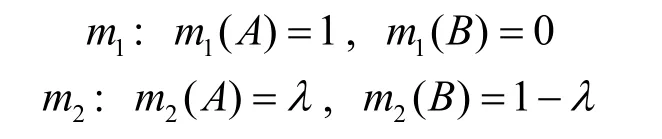
当λ 的变化范围为[0,1]时，图 3 展示了1 -Cor[12]、1 -r[18]、BJS[19]和BEMD 随λ 变化的冲突度量曲线。

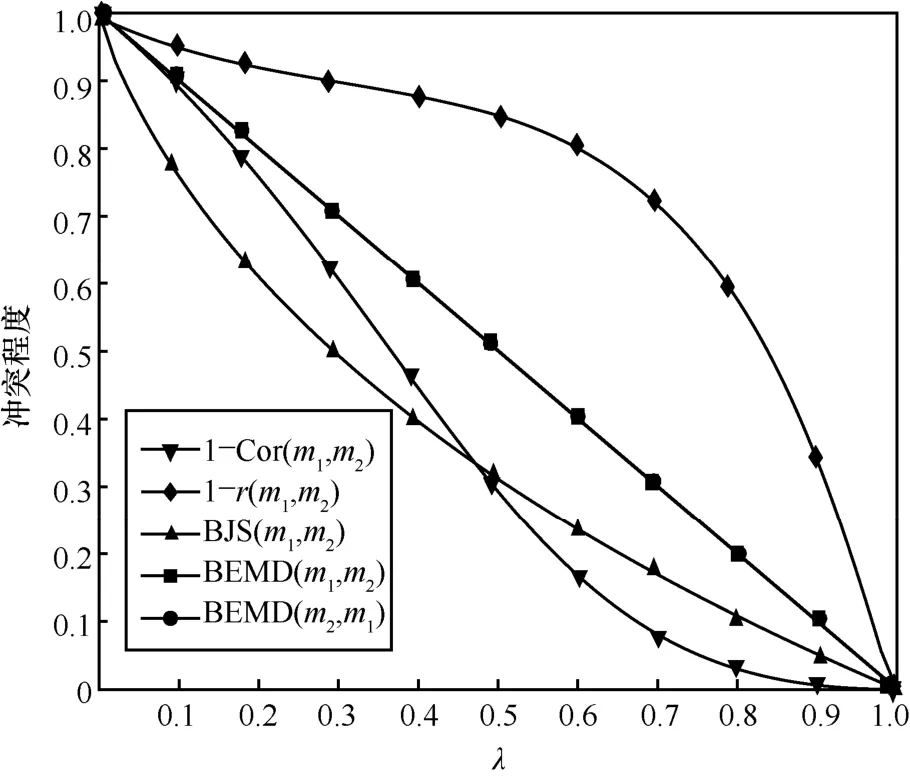
图3 不同方法随λ 变化的冲突度量曲线

图3 所示的4 种证据冲突度量方法的趋势基本相同，但BEMD 的曲线随着λ 的变化更接近线性，这说明了 BEMD 的优越性。由图 3 可知，BEMD(m1,m2)和 BEMD(m2,m1)的冲突度量曲线是一致的，这验证了 BEMD(m1,m2)满足对称性。在λ的变化过程中，BEMD∈[0,1]，并且当λ=0时BEMD=1，而当λ=1时BEMD=0，以上验证了BEMD 满足ECSMF 的期望特征1)～特征4)，即对称性、规范性、同一性和互斥性。

下面通过例7 验证BEMD 满足ECSMF 的期望特征5)，即三角不等式。

例7假设识别框架Θ={ A, B ,C ,D}中有3 个证据m1、m2和m3，每个证据的BPA 为

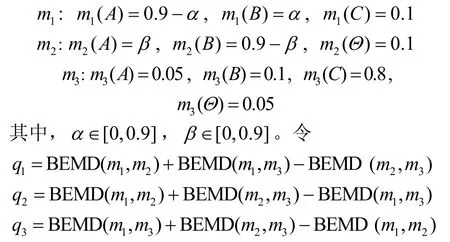
如图4 所示，随着变量α 和β 分别从0 增加到0.9，qi≥ 0，i=1,2,3，可以看到BEMD 满足三角不等式。

为了进一步说明BEMD 的有效性，下面通过例8考查在焦元和质量都发生变化的情况下BEMD 的变化趋势。

就在众多企业为了营造品牌的经典感而不断增厚品牌“履历”的时候，青岛啤酒这个百年品牌却抛出了“品牌不是越老越好”的观点。这家拥有115年历史的啤酒品牌一直不太提及自己是“中华老字号”，中华老字号的标志——金石篆刻手法将“字”“号”融合的印章造型也从没有出现在青岛啤酒任何产品的包装上。

例8本例采用文献[20]的例子，假设识别框架Θ={S1,S2,…,S19}中存在2 个证据m1和m2，它们的BPA 分别为

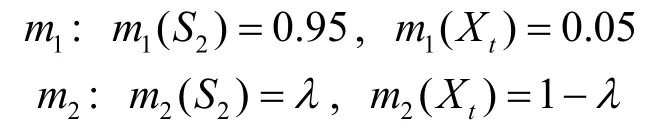
其中，Xt是一个变量集合，Xt=[S1,…,St]，t=1,…,19；λ 的变化范围为[0.05,0.95]。

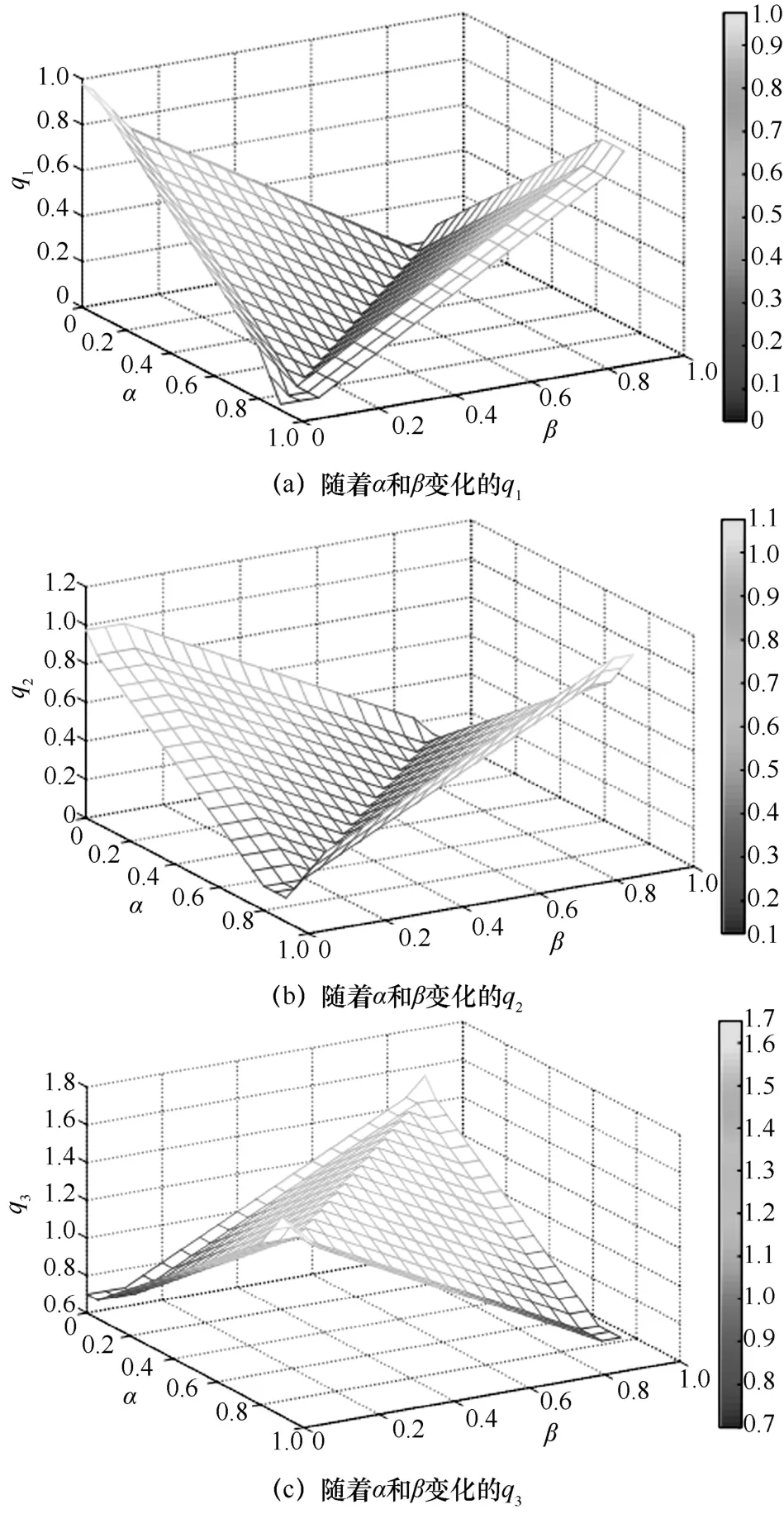
图4 随着α 和β 变化的 q1、q2和 q3

由图5(a)和图5(d)可知，无论λ 和Xt如何变化，BEMD(m1,m2)∈[0,1]。从图5(b)中可以看出，无论集合Xt如何变化，m1与m2之间的冲突程度都会随着λ 的增加而减小。从图5(c)中可以看出，在λ 固定的情况下，当 t=1时，S2和Xt之间没有交集，证据m1与m2之间容易出现高度冲突的情况；当 t=2时，Xt={S1,S2}和S2之间的相关程度最高，证据m1与m2都对S2有相对较高的支持度，所以当λ 的值不变时，证据m1与m2之间的冲突程度相对较低。随着焦元Xt的基数t从2 增加到19，证据间的冲突度量逐渐增加，这与直观分析相符。图5(a)～图5(d)均表明BEMD 符合ECSMF 的不反直观性。

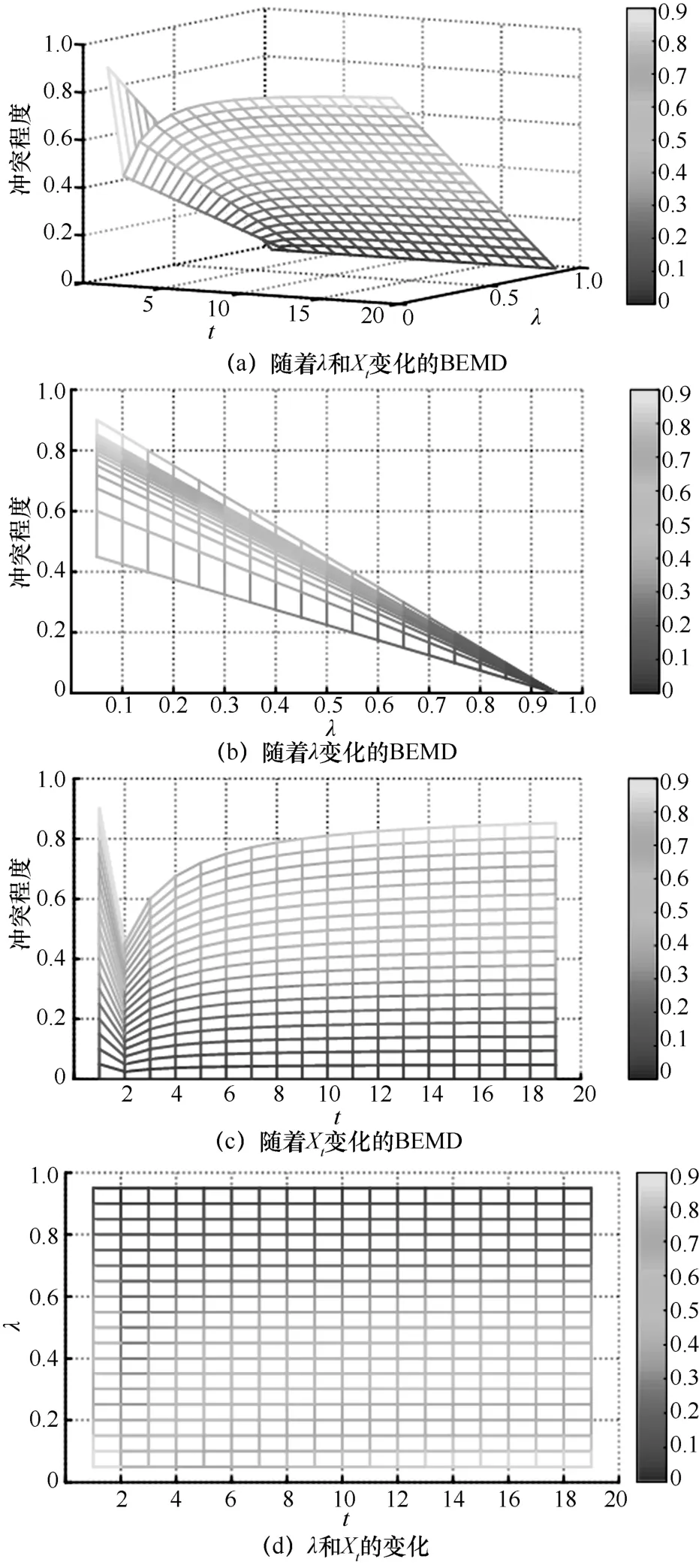
图5 在λ 和Xt不同情况下的冲突度量

5 结束语

D-S 证据理论是一种重要的多传感器信息融合决策方法，然而，在处理高度冲突证据时往往会得出反直观的结论，在解决该问题时首先需要对证据冲突进行准确的度量。为了度量准确，本文首先提出ECSMF的期望特征，然后根据期望特征的要求，提出了一种基于EMD 的证据冲突度量方法，即BEMD，该方法使用Jaccard 集合距离对EMD 进行优化，不需要预先对证据进行修正，也不要求不同证据中的焦元数量完全相同，并且可以直接处理带复合焦元的BPA，理论证明和实例仿真验证了所提方法可以有效地度量证据间的冲突大小。证据理论的冲突度量是研究冲突证据合成方法的基础，而本文的冲突度量方法中并未涉及证据的合成方法，在未来的工作中，如何基于BEMD 拓展冲突证据合成规则将是笔者主要的研究内容。