两层单跨缩尺RC框架结构外爆炸试验数值模拟

吴 昊，林 城

(同济大学 土木工程学院，上海 200092)

0 引 言

钢筋混凝土(RC)框架结构作为最普遍的民用结构形式，在服役期间可能受到军事、恐怖爆炸袭击以及偶然性爆炸事故威胁。爆炸产生的冲击波和破片不仅对附近人员和财产造成重大威胁，而且可能导致结构关键支撑构件失效，甚至引发结构局部或整体倒塌。因此，开展RC框架结构的抗爆研究具有重要的研究价值和现实意义。

目前，国内外学者已对爆炸荷载作用下RC构件动态响应和损伤破坏开展了大量试验研究。Getchell等[1]开展了一系列单向RC板的爆炸试验，发现单向RC板在不同爆炸荷载作用下可能出现直剪、弯曲、弯剪的破坏形式。Woodson等[2]将爆炸荷载等效为均布荷载，开展了10组单向板的爆炸试验，研究了加劲肋对板抗爆性能的影响。Duranovic[3]开展了5组四边简支、1∶2.5缩尺RC板的爆炸试验，验证了比例缩放建模的有效性。张想柏等[4]开展了有限厚度RC板的接触爆炸试验，研究了震塌对防爆结构的破坏效应，并采用LS-DYNA较好地重现了试验过程，提出了新的震塌厚度计算公式。Morrill等[5]开展了3组足尺RC柱的爆炸试验，研究了爆炸荷载作用下RC柱抗力大小和相关加固措施，提出了简化加固设计程序。

大型爆炸试验具有难度大、成本高和爆炸作用过程复杂的特点，因此有关整体RC结构在爆炸荷载作用下的动态响应和损伤破坏的研究较少，且主要针对缩尺结构和框架子结构[6-10]。Woodson[11]开展了1/4缩尺9开间地下室的爆炸试验，研究了爆炸荷载对木柱加固前后地下室模型的动态响应破坏效应，并对加固措施的有效性进行评估。Woodson等[12-14]还开展了1/4缩尺2层RC框架的爆炸试验，研究了爆炸荷载对框架柱的破坏效应及填充墙对框架柱破坏效应的影响。高超等[15]开展了1/8缩尺3榀3层3开间RC框架结构的爆炸试验，研究了不同炸药量、起爆位置对结构动态响应、破坏模式的影响。龚敏[16]开展了1/2缩尺2层2跨框架结构的爆炸试验，研究了不同炸药量、爆炸距离对框架结构动态响应的影响。

数值模拟作为结构分析的常用手段，具有经济、有效的优点，但由于算力限制，已有爆炸荷载作用下RC框架结构的数值模拟研究主要存在以下不足：未考虑结构围护条件，主要针对开口框架结构；将爆炸荷载简化为等效荷载施加，无法考虑爆炸冲击波的传播及其与结构相互作用；大部分数值模拟结果未通过真实结构试验验证。Abdullah[17]采用LS-DYNA研究了爆炸荷载作用下3层2跨RC框架结构的响应情况，并与GSA、DoD规范方法的计算结果进行对比。黄真伟[18]采用LS-DYNA研究了爆炸荷载作用下平面和空间RC框架结构边柱、中柱失效后的倒塌情况。师燕超等[19]采用LS-DYNA研究了爆炸荷载作用下3层2跨RC框架结构的连续倒塌行为，并对GSA方法进行修正。Sasani等[20]采用SAP2000研究了爆炸荷载作用下10层RC结构在发生初始局部破坏后的抗倒塌能力。阎石等[21]采用ABAQUS，通过移除底层中柱的方式，研究了爆炸荷载作用下10层RC框架结构的倒塌机理。匡志平等[22]采用LS-DYNA研究了爆炸荷载作用下3层RC框架结构的动态响应，分析了装药量、截面形式、钢筋布置形式和配筋率对结构响应的影响。何庆锋等[23]采用LS-DYNA研究了4层2跨RC框架结构在爆炸移除底层柱后的动态响应和损伤破坏。姚宇飞[24]采用LS-DYNA研究了爆炸荷载作用下4层2跨RC框架结构在底层中柱、边柱失效后的动态响应和倒塌过程。Jayasooriya等[25]分别采用SAP2000和LS-DYNA评估了10层RC框架结构在近区爆炸下整体和局部的响应行为。

本文基于已有1/4缩尺RC框架结构的爆炸试验，采用LS-DYNA研究爆炸荷载作用下开口框架、带填充墙框架、带部分开洞填充墙框架、车库4种结构形式的动态响应行为，通过对比爆炸冲击波超压、冲量时程、结构局部及整体响应情况，验证本文所采用的数值仿真算法、材料本构模型及其参数取值的适用性，为后续原型RC框架结构抗爆响应和破坏倒塌分析提供有益的参考。

1 试验简介

美国陆军工程兵团水道试验站(WES)[12]于1999年开展了1/4缩尺2层RC框架结构爆炸试验，研究了爆炸荷载对框架柱的破坏效应及填充墙对框架柱破坏的影响。试验框架为1/4缩尺2层单跨钢筋混凝土结构，楼板厚度为41 mm，中柱尺寸为89 mm×89 mm。混凝土抗压强度为38.5 MPa，钢筋抗拉强度为400～450 MPa，直径2～25 mm。框架中柱顶部设置重物作为上部结构荷载，约为2.1 MPa，框架背面设置扶壁，表征其余结构的支撑作用。试验采用半球形C4炸药，其底面距地面230 mm，研究对象根据炸药量、爆距和围护条件共分为5种工况，如表1所示。试验设置及测点位置如图1所示，共布置7个反射超压传感器，其中3个(F1、F2、F3)位于框架中柱正面、2个(B1、B2)位于中柱背面、2个(R1、R2)布置于F1测点关于炸药的对称位置并作为参考测点。更多试验细节详见文献[12]。

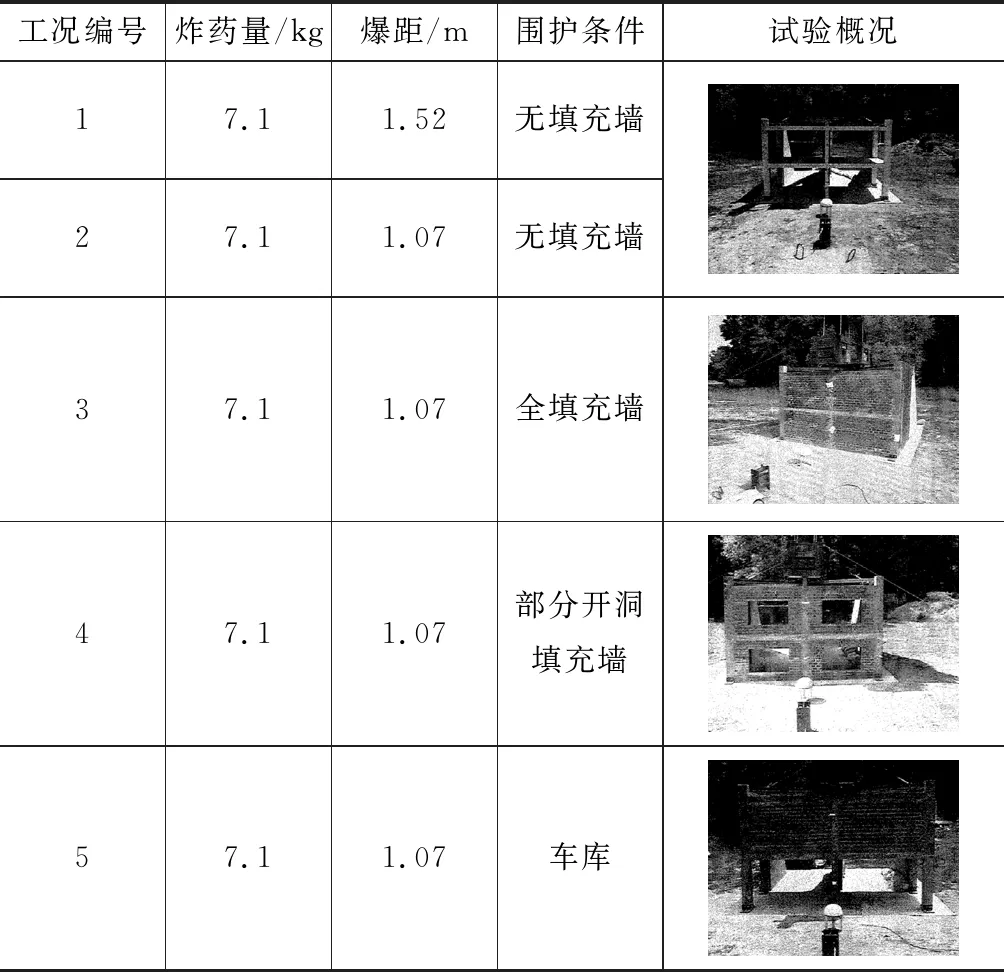
表1 试验工况Table 1 Test Scenarios

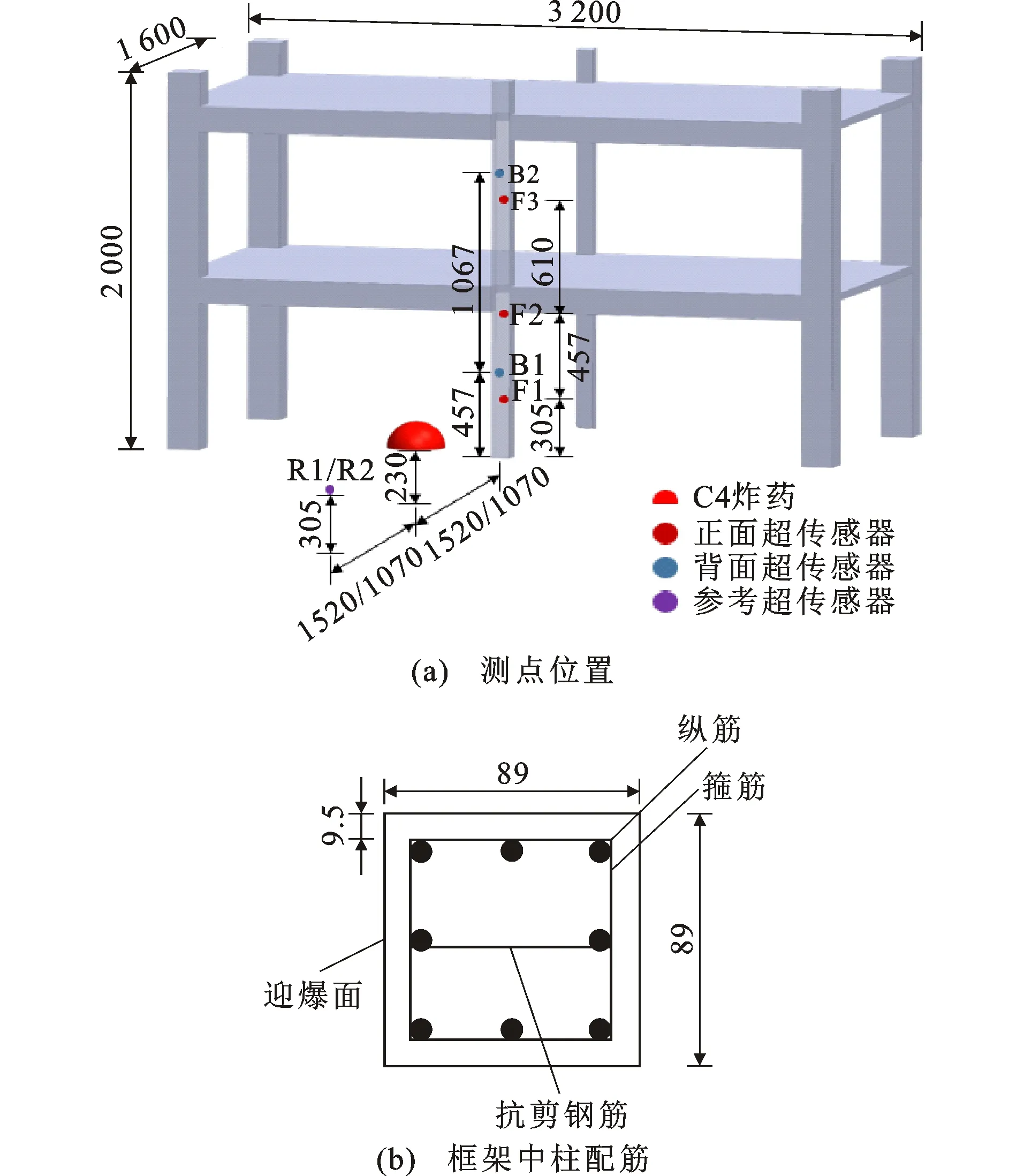
图1 试验设置(单位：mm)Fig.1 Test Setup (Unit:mm)

2 有限元模型建立与验证

本节采用LS-DYNA对文献[12]中全部试验工况进行有限元模拟分析，通过任意拉格朗日欧拉算法(ALE)和流固耦合算法(FSI)实现爆炸冲击波的传播及其与结构相互作用。

2.1 有限元模型

基于文献[12]中框架结构的尺寸和配筋，建立相应的有限元模型，如图2所示。

图2 有限元模型Fig.2 Finite Element Model

单元类型和网格尺寸方面，混凝土及填充墙采用Solid164单元，钢筋采用Beam188单元，空气、炸药采用Euler单元；RC框架结构的网格尺寸为10 mm×10 mm，填充墙网格尺寸为50 mm×50 mm，局部砂浆网格尺寸为5 mm×5 mm。以通过炸药中心并平行于结构正面的几何面为对称面，对各工况空气、炸药模型进行简化，网格尺寸为50 mm×50 mm。

接触算法方面，空气和炸药、各混凝土构件间采用共节点接触；钢筋和混凝土、空气炸药和框架结构间采用*CONSTRAINED_LAGRANGE_IN_SOLID流固耦合接触；其余接触均采用*AUTOMATIC_SURFACE_TO_SURFACE自动面面接触定义。

荷载施加和边界条件方面，通过*LOAD_SEGMENT_SET将重力荷载等效为均布荷载施加于柱顶，大小为2.1 MPa；通过*LOAD_BODY_Y对结构施加重力；不考虑土体变形，假设地面为无限大刚性地面，通过*RIGIDWALL_PLANAR_FINITE创建；采用*BOUNDARY_NON_REFLECTING在空气边界设置无反射(流出)边界。空气域对称面设置对称约束；主体结构背部、底部设置约束，分别表征扶壁、地面对结构的支撑作用；以上自由度约束均通过*BOUNDARY_SPC_SET定义。

2.2 材料模型

2.2.1 混凝土

混凝土采用*MAT_CONCRETE_DAMAGE_REL3模型，即K&C材料模型。该模型能够较好地表征混凝土塑性流动、损伤效应、应变率效应等材料特性，并广泛应用于爆炸荷载下混凝土动态响应的模拟。K&C模型中采用动态放大系数(DIF)考虑混凝土的应变率效应。其中，混凝土抗拉、抗压强度的DIF由式(1)、(2)确定[26]。

(1)

(2)

为了模拟混凝土的压碎和剥落，通过*MAT_ADD_EROSION定义了混凝土材料的失效准则。由于失效应变与单元网格尺寸有关，通过与试验对比，本文失效应变(最大主应变限值)取0.3。

2.2.2 钢 筋

钢筋采用*MAT_PLASTIC_KINMATIC材料模型，该模型是一种与应变率相关并考虑了单元失效的双线性材料模型，可以通过改变硬化参数的取值来选择各项同性硬化(β=1)、随动硬化(β=0)或混合硬化方式(0<β<1)。应变率采用的Cowper-Symonds模型[27]为

(3)

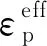
2.2.3 砖、砂浆

砖、砂浆采用*MAT_BRITTLE_DAMAGE材料模型，该模型为一种各向异性的脆性破坏模型，当材料受拉时，其弹性强度和剪切强度会随着裂缝的产生而降低，弹性刚度相应减小。

2.2.4 空 气

空气可视为无黏性理想气体，采用*MAT_NULL材料模型，其状态方程用*EOS_LINEAR_POLYNOMIAL线性多项式方程(4)[27]描述。

Pa=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E0

(4)

式中：Pa为空气压力；C0～C6为状态方程常数；E0为初始内能；μ为动态黏性系数，μ=1/(V-1)，V为相对体积。

2.2.5 炸 药

采用*MAT_HIGH_EXOLOSIVE_BURN材料模型和*EOS_JWL状态方程描述TNT炸药的爆轰过程。该模型忽略炸药点燃伊始的化学反应过程，仅考虑反应的终态热并将其作为分析的初始条件，通过状态方程式(5)描述炸药爆炸产物压力[27]。

(5)

式中：Pe为爆轰压力；A、B、R1、R2、ω均为材料参数，由试验确定。

主要的材料模型参数取值如表2所示。

2.3 网格敏感性分析

2.3.1 炸药形状简化

为了简化建模并提高计算效率和稳定性，分别采用半球形、立方体炸药建模对爆炸过程进行模拟，TNT等效系数取为1.25[28]，则C4炸药等效TNT装药量为8.9 kg。图3给出了不同炸药形状所得框架中柱位置的反射超压沿柱高度方向分布情况。从图3可以看出：立方体炸药的反射超压模拟值与半球形炸药接近，二者仅在高度500 mm以下有较小偏差。因此，采用立方体炸药代替半球形炸药进行后续分析。

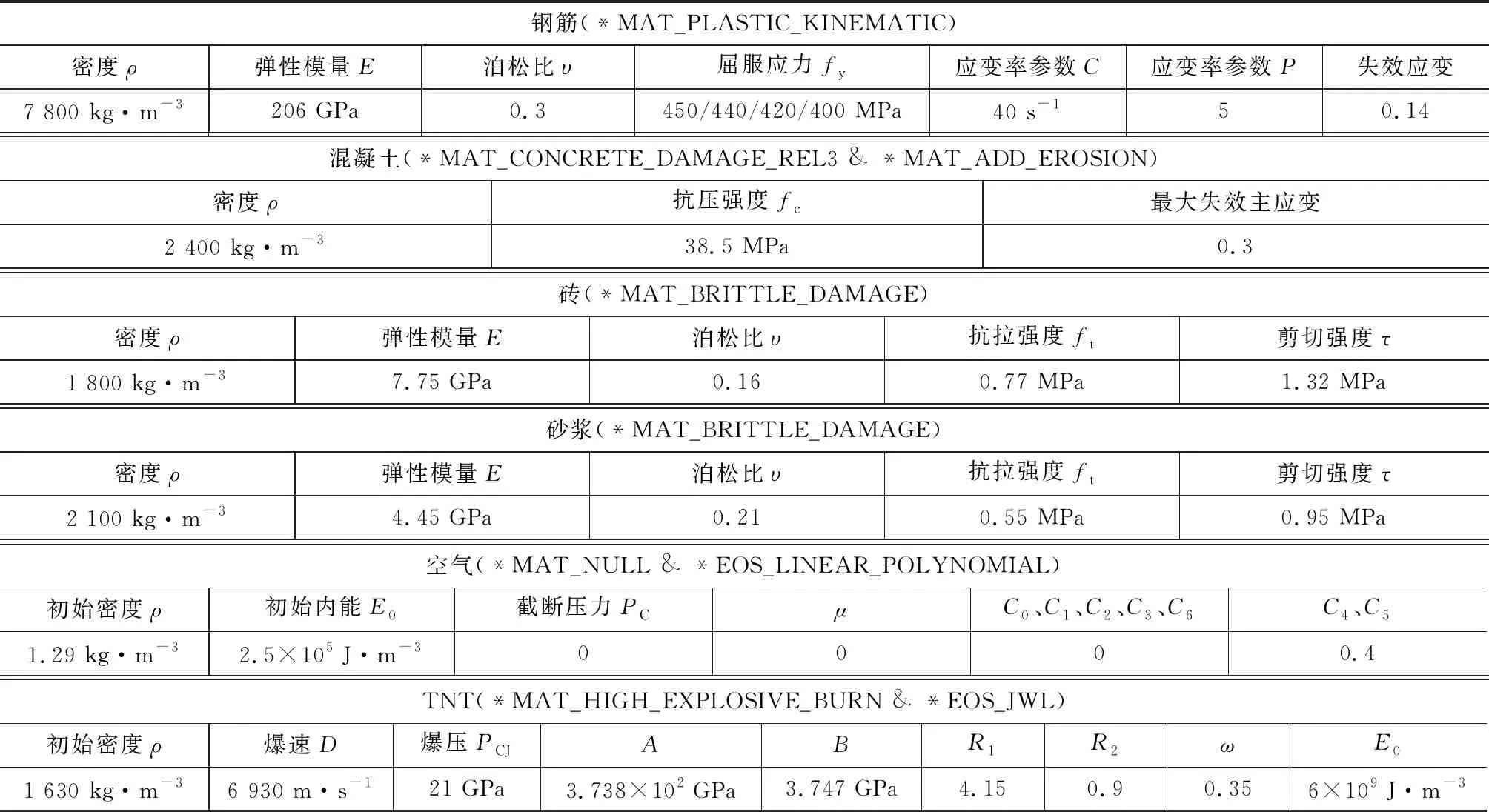
表2 材料模型参数Table 2 Material Model Parameters

图3 不同炸药形状反射超压沿柱高度方向分布Fig.3 Reflected Overpressure Distributions Along Column Height for Different Explosive Shapes

2.3.2 网格敏感性分析

图4 试验和数值模拟的反射超压沿柱高度方向分布对比Fig.4 Comparisons of Reflected Overpressure Distributions Along Column Height Between Experiment and Numerical Simulation

为了真实反映试验爆炸荷载，开展空气和炸药模型中网格尺寸影响的收敛性分析。以工况1框架中柱位置的反射超压为评价指标，空气和炸药网格尺寸分别为30 mm×30 mm、40×40 mm、50 mm×50 mm，试验和数值模拟结果的对比如图4所示。从图4可以看出：试验值本身存在较大相对误差，F1、R1、R2测点正面超压相对误差大于50%，其余测点超压模拟值均小于试验值；不同网格尺寸所得超压同样呈明显的梯度分布，但在地面附近的模拟值较试验值偏大，原因为有限元模型采用刚性地面导致地面反射超压偏大；正面超压误差随网格尺寸的减小而增大，背面超压误差较小。

因此，当空气和炸药网格尺寸取50 mm×50 mm时，模拟值与试验值数量级相同，相应超压分布情况与试验吻合较好，能够较为准确地预测爆炸冲击荷载，故采用50 mm×50 mm网格尺寸进行后续分析。

3 有限元结果及其分析

根据网格敏感性分析，确定了空气和炸药的网格尺寸，通过对比工况1～5试验和数值模拟得到的爆炸冲击波传播过程、测点超压时程、冲量时程、结构局部及整体响应情况，进一步验证数值模拟方法、材料模型与参数取值的正确性和适用性。

3.1 工况1开口框架

3.1.1 工况1超压时程

图5为工况1不同时刻t爆炸冲击波传播云图。可以看出，爆炸冲击波经历了地面反射、结构反射和绕射的典型传播过程。

图5 工况1不同时刻冲击波传播云图Fig.5 Propagation Contours of Blast Waves at Different Instants in Scenario 1

图6 工况1试验和数值模拟的反射超压沿柱高度方向分布对比Fig.6 Comparisons of Reflected Overpressure Distributions Along Column Height Between Experiment and Numerical Simulation in Scenario 1

图7 工况1试验和数值模拟的测点反射超压时程对比Fig.7 Comparisons of Reflected Overpressure-time History of Measuring Points Between Experiment and Numerical Simulation in Scenario 1

图6、7分别对比了工况1试验和数值模拟的框架中柱超压分布以及测点的超压时程曲线。可以发现：F1测点的超压模拟值与试验值接近，F2、F3测点的模拟值则偏小；中柱背面超压模拟值与试验值吻合较好，在高度750、1 500 mm，即楼层交界处出现极大值；模拟值与试验值相比存在起爆时间滞后、超压峰值相差大等问题，原因可能为超压传感器存在偏差导致二者起爆时间不一致或反射超压传感器在试验中发生损坏等。

3.1.2 工况1冲量时程

图8对比了工况1试验和数值模拟的框架中柱冲量沿高度方向分布情况。可以看出，冲量模拟值在结构1层(高度750 mm)以上部分与试验值相差较小，而在750 mm以下临近地面部分的模拟值偏大，原因是有限元模型采用刚性地面，造成反射超压偏大，相应积分得到的冲量值偏大。

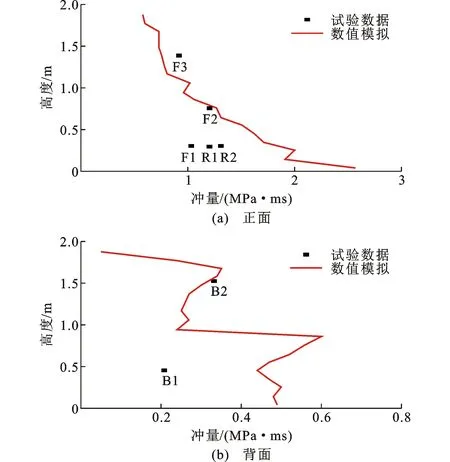
图8 工况1试验和数值模拟的冲量沿高度方向分布对比Fig.8 Comparisons of Impulse Distributions Along Column Height Between Experiment and Numerical Simulation in Scenario 1

3.1.3 工况1结构响应

图9对比了工况1试验和数值模拟的下层框架中柱跨中位移时程曲线。模拟值与试验值相比偏大，模拟得到下层柱最大位移为7 mm，残余位移为3 mm，误差较小。

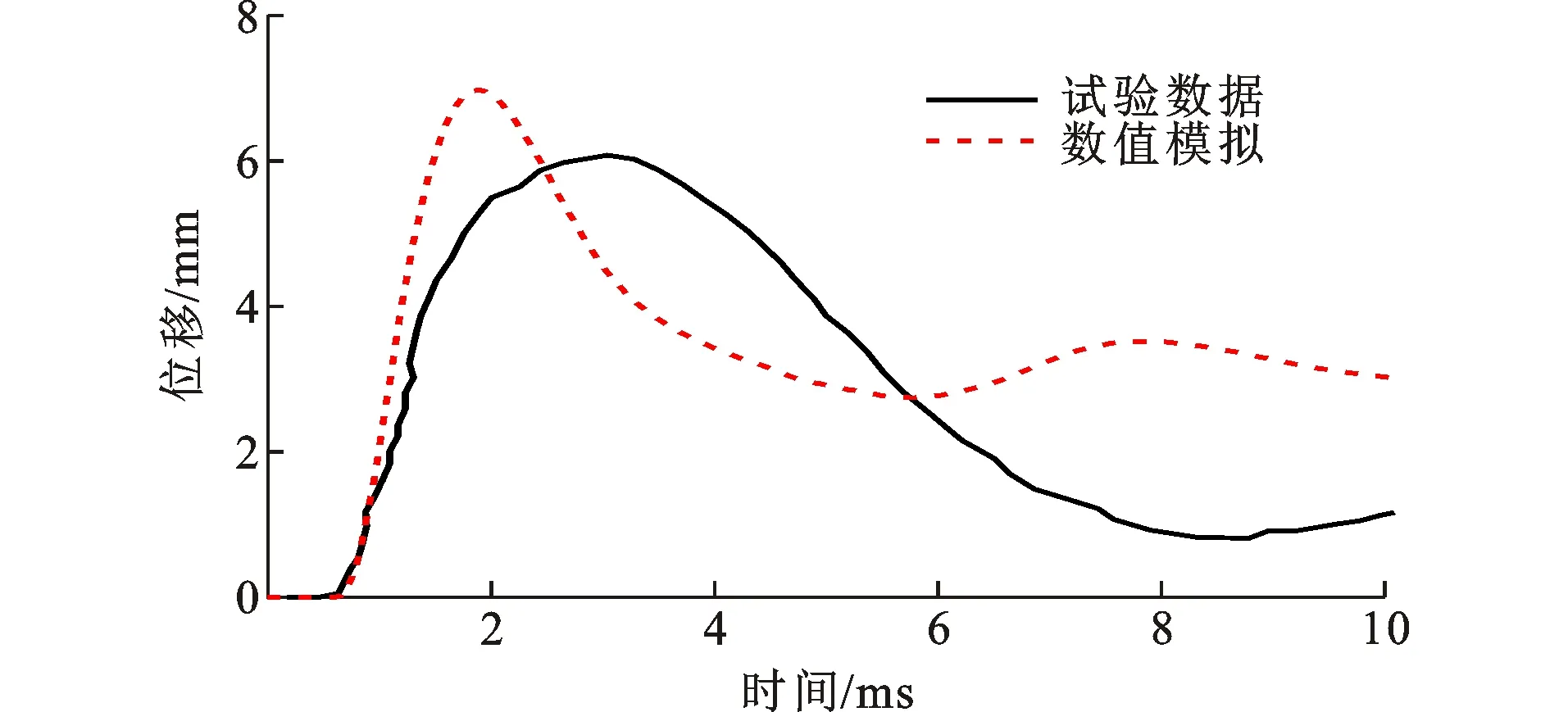
图9 工况1试验和数值模拟的下层柱跨中位移时程对比Fig.9 Comparisons of Mid-span Displacement-time Histories of Lower Column Between Experiment and Numerical Simulation in Scenario 1

图10为工况1结构整体损伤破坏云图。随着爆炸冲击波的传播，下层柱首先受到冲击作用，正面混凝土受压，背面混凝土受拉，柱脚和柱顶位置出现较大变形；随后冲击波继续在框架内部传播并在楼板上下表面产生压力差，1层楼板出现上拱破坏，上部混凝土受拉开裂形成1条通长的裂缝。

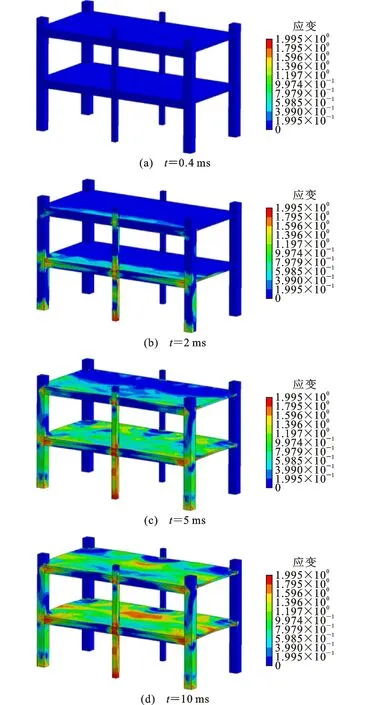
图10 工况1结构整体损伤破坏云图Fig.10 Overal Damage Contours of Structure in Scenario 1

3.2 工况2开口框架

3.2.1 工况2超压时程

图11为工况2不同时刻爆炸冲击波传播云图，爆炸冲击波传播过程与工况1类似。

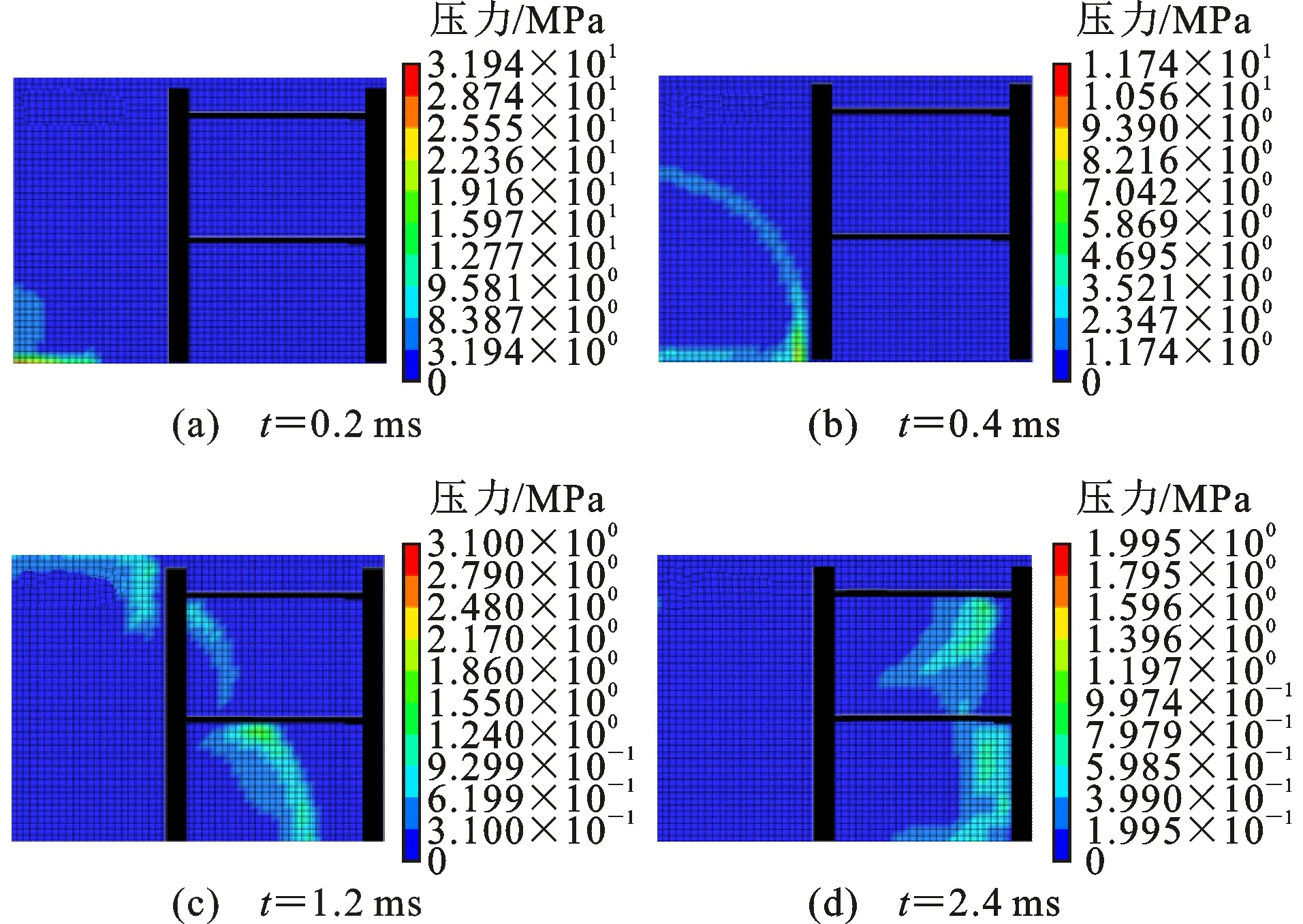
图11 工况2不同时刻冲击波传播云图Fig.11 Propagation Contours of Blast Waves at Different Instants in Scenario 2

图12为工况2试验和数值模拟的正面反射超压结果。中柱正面超压试验值存在较大的离散性，F1、R1、R2测点自身试验值相对误差大于20%，仅F2测点模拟值与试验值接近，超压峰值相对误差小于5%。

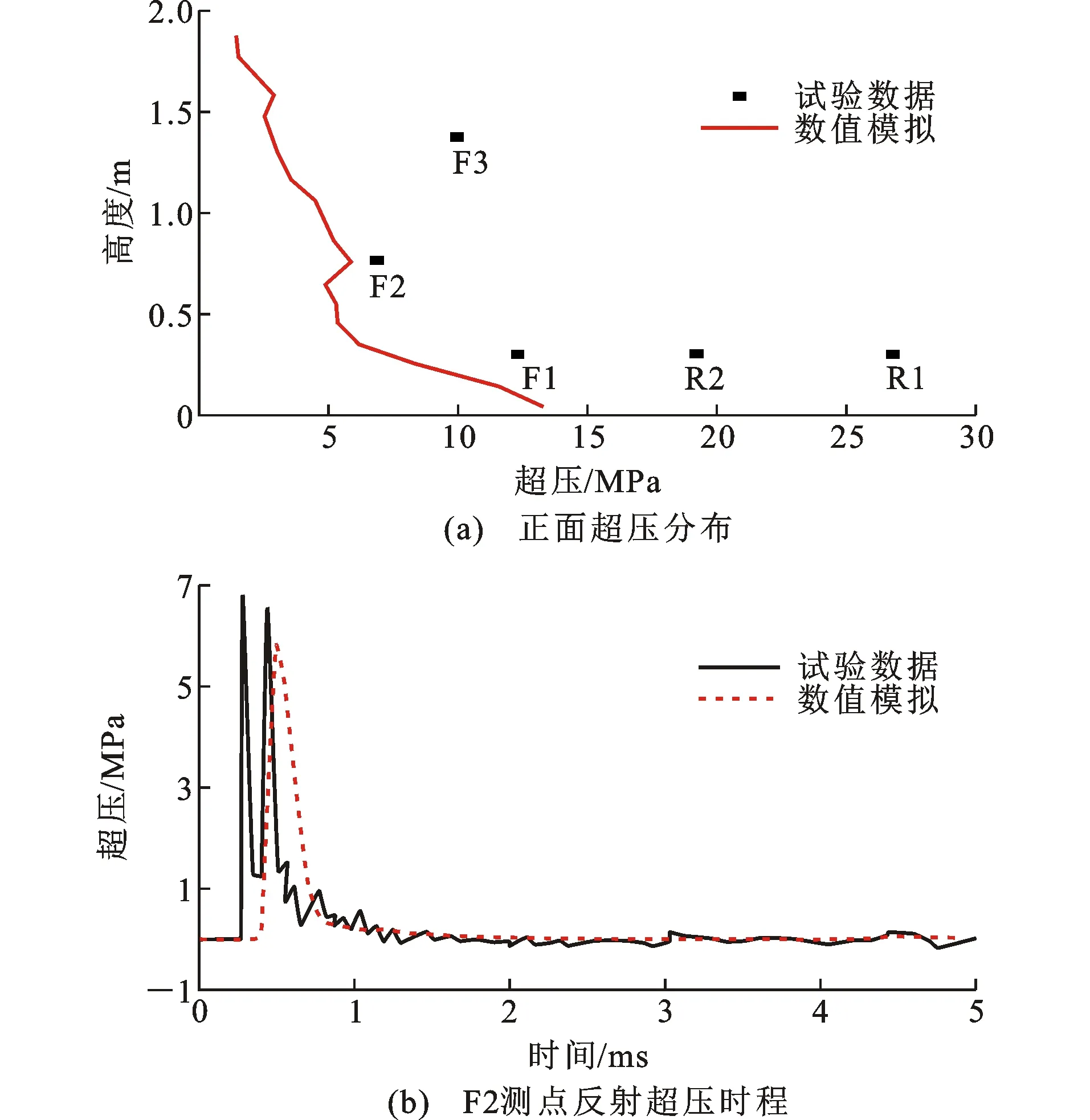
图12 工况2试验和数值模拟的正面反射超压结果对比Fig.12 Comparisons of Reflected Overpressure in Front of Column Between Experiment and Numerical Simulation in Scenario 2

3.2.2 工况2冲量时程

图13对比了工况2试验和数值模拟的框架中柱冲量沿高度方向分布情况。由于测量装置损坏，B1测点的冲量测量值未给出；其余测点处冲量模拟值与试验值相近，各点相对误差均不超过5%；地面附近的冲量模拟值偏大。

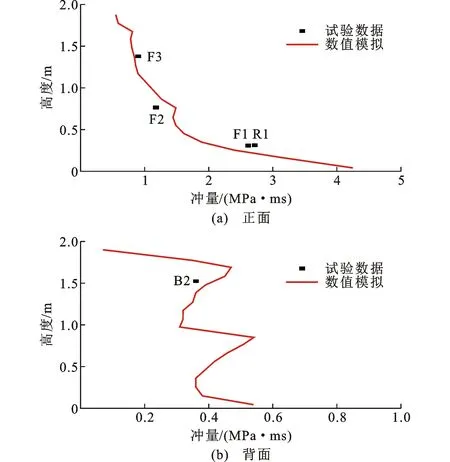
图13 工况2试验和数值模拟的冲量沿柱高度方向分布对比Fig.13 Comparisons of Impulse Distributions Along Column Height Between Experiment and Numerical Simulation in Scenario 2

3.2.3 工况2结构响应

图14对比了工况2试验和数值模拟的下层框架中柱跨中位移时程曲线。与试验数据相比，数值模拟结果更符合试验测量情况，模拟得到的最大位移为14 mm，残余位移为9.5 mm，相对误差均不超过20%。

图14 工况2试验和数值模拟的下层柱跨中位移时程对比Fig.14 Comparisons of Mid-span Displacement-time Histories of Lower Column Between Experiment and Numerical Simulation in Scenario 2

图15为工况2结构整体损伤破坏云图。结构破坏过程与工况1类似，但由于爆距减小，作用于结构的爆炸荷载明显增大，结构破坏更为严重；1层楼板跨中位置上拱70 mm，与试验值64 mm接近，2层楼板破坏较小，结构整体裂缝分布与试验一致；下层柱底部发生明显变形，而顶部破坏较小，仍能够承受结构荷载，符合试验结果。

3.3 工况3带填充墙框架

3.3.1 工况3超压时程

图16为工况3不同时刻爆炸冲击波传播云图。由于填充墙的存在，爆炸冲击波在传播至结构位置后大部分发生反射。

图17为工况3试验和数值模拟的正面反射超压结果对比。可以发现：结构高度300 mm以下的正面超压模拟值与试验值接近，其余位置的模拟值偏小。

3.3.2 工况3冲量时程

图18对比了工况3试验和数值模拟的框架中柱正面冲量沿高度方向分布情况。可以看出：正面冲量模拟值与试验值吻合较好，仅在临近地面部分偏大，主要原因为模型采用刚性地面。

3.3.3 工况3结构响应

图19对比了工况3试验和数值模拟的下层框架中柱跨中位移时程曲线和损伤破坏。下层柱最大位移模拟值为105 mm，与试验值相差10 mm，柱顶沉降约25 mm；构件整体呈弯曲破坏，与试验结果相符。

图15 工况2结构整体损伤破坏云图Fig.15 Overall Damage Contours of Structure in Scenario 2

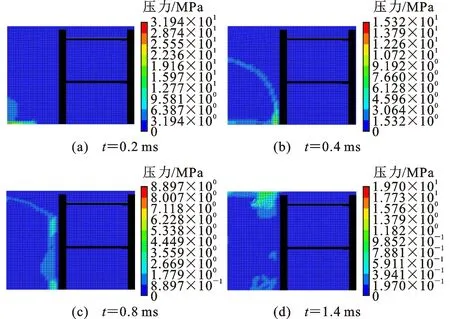
图16 工况3不同时刻冲击波传播云图Fig.16 Propagation Contours of Blast Waves at Different Instants in Scenario 3

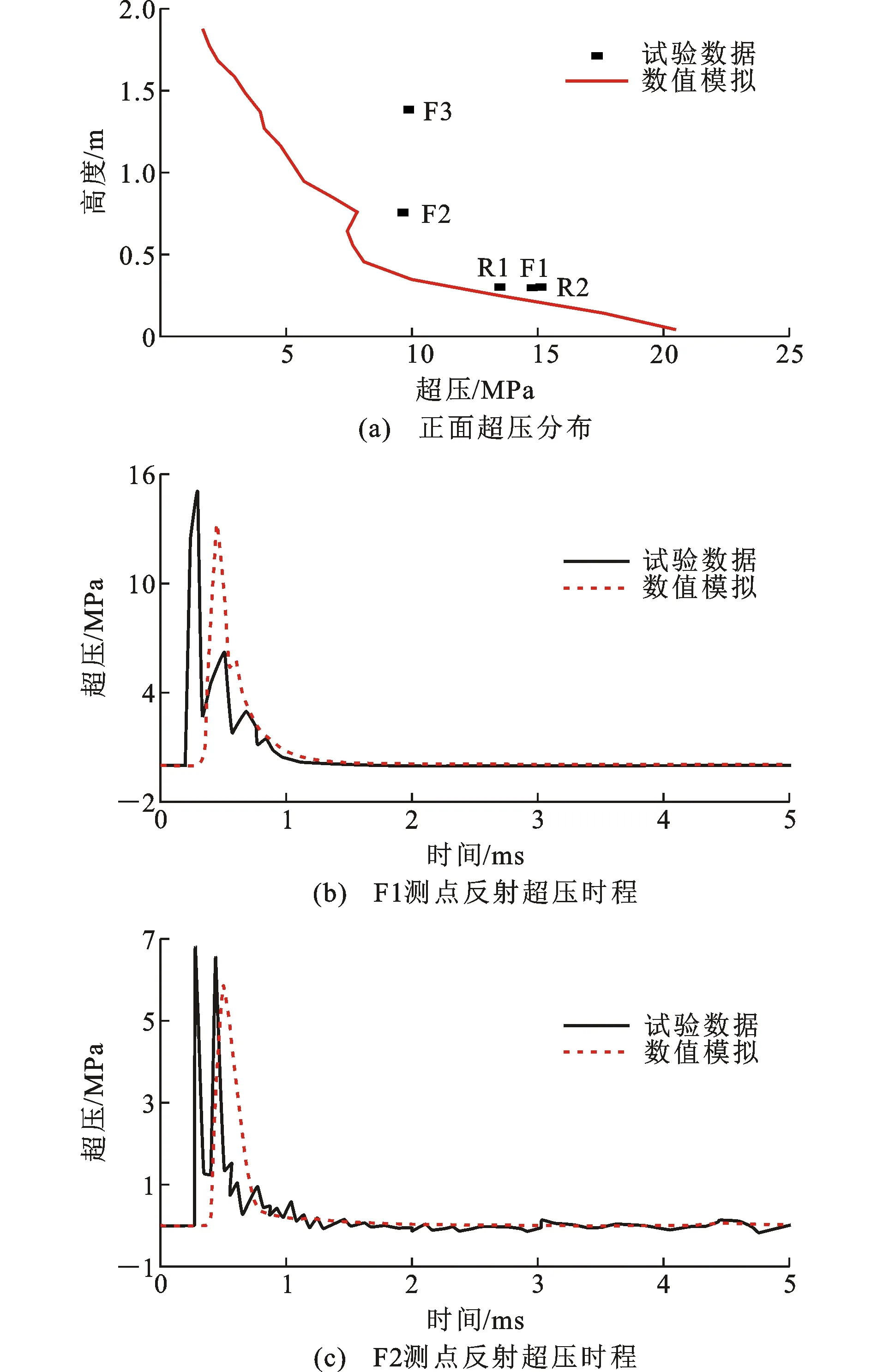
图17 工况3试验和数值模拟的正面反射超压结果对比Fig.17 Comparisons of Reflected Overpressure in Front of Column Between Experiment and Numerical Simulation in Scenario 3

图18 工况3试验和数值模拟的正面冲量沿柱高度方向分布对比Fig.18 Comparisons of Impulse Distributions in Front of Column Along Column Height Between Experiment and Numerical Simulation in Scenario 3

图19 工况3试验和数值模拟的下层柱跨中位移时程曲线和损伤破坏对比Fig.19 Comparisons of Mid-span Displacement-time History and Damage of Lower Column Between Experiment and Numerical Simulation in Scenario 3

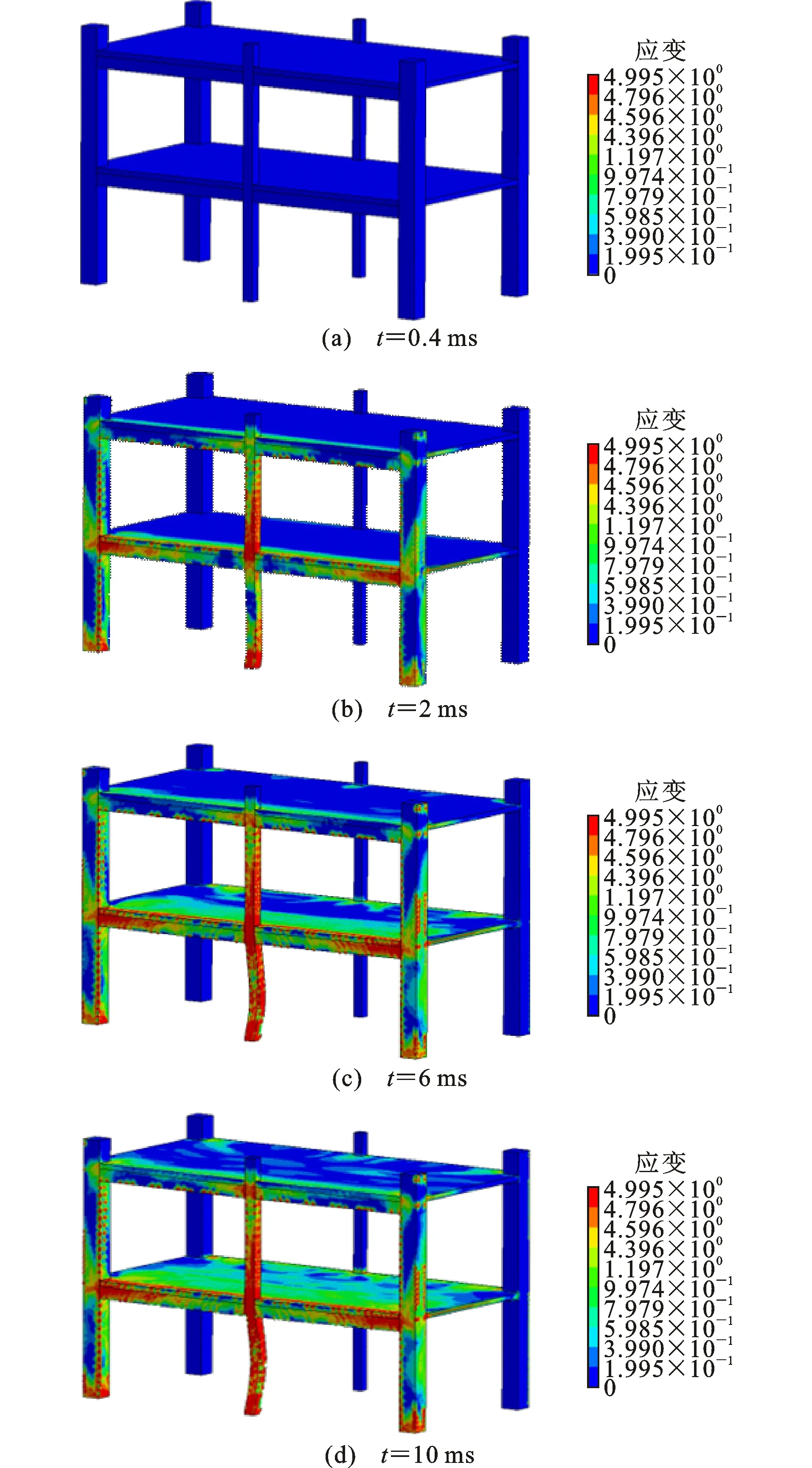
图20 工况3主体结构整体损伤破坏云图Fig.20 Overall Damage Contours of Main Structure in Scenario 3

图21 工况3填充墙整体损伤破坏云图Fig.21 Overall Damage Contours of Infilled Wall in Scenario 3

图20、21分别为工况3主体结构和填充墙损伤破坏云图。爆炸冲击波与填充墙和框架柱相遇后发生反射，填充墙与主体结构连接处砂浆删除，墙体发生剪切破坏，部分砖块飞出；小部分冲击波穿过墙体继续在结构内部传播，相应楼板仅出现裂缝；迎爆面下层柱及结构连接处发生严重破坏，此时边梁起连接作用，将破坏位置附近的力传递给周围构件，避免结构发生连续性倒塌。

3.4 工况4带部分开洞填充墙框架

3.4.1 工况4超压时程

图22为工况4不同时刻爆炸冲击波传播云图。爆炸冲击波经地面反射后，沿填充墙开洞进入结构内部继续传播。

图22 工况4不同时刻冲击波传播云图Fig.22 Propagation Contours of Blast Waves at Different Instants in Scenario 4

图23为工况4试验和数值模拟的正面反射超压结果对比。可以发现：F1、R1、R2测点正面超压试验值之间误差较大，模拟值与三者试验值均值相对误差大于30%，F2测点超压模拟值与试验值相对误差小于20%。

图23 工况4试验和数值模拟的正面反射超压结果对比Fig.23 Comparisons of Reflected Overpressure in Front of Column Between Experiment and Numerical Simulation in Scenario 4

3.4.2 工况4冲量时程

图24对比了工况4试验和数值模拟的框架中柱正面冲量沿高度方向分布情况。可以看出：中柱正面冲量模拟值与试验值吻合较好，相对误差均小于5%；正面冲量在地面附近存在明显的梯度分布。

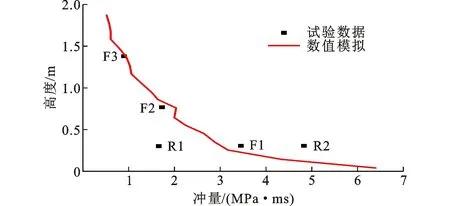
图24 工况4试验和数值模拟的正面冲量沿高度方向分布对比Fig.24 Comparisons of Impulse Distributions in Front of Column Along Column Height Between Experiment and Numerical Simulation in Scenario 4

3.4.3 工况4结构响应

由于试验未给出工况4下层框架柱跨中位移数据，图25仅对比其损伤破坏。下层柱底部和顶部在试验中出现明显剪切破坏，而数值模拟结果仅在柱底出现类似现象，原因可能为填充墙与结构接触的参数设置问题，或地面附近超压过大导致底部砂浆过早删除，相应填充墙受力边界条件发生改变，无法准确描述实际情况。

图25 工况4试验和数值模拟的下层柱损伤破坏对比Fig.25 Comparisons of Damage of Lower Column Between Experiment and Numerical Simulation in Scenario 4

图26、27分别为工况4主体结构和填充墙损伤破坏云图。爆炸冲击波与结构相互作用造成墙体剪切破坏、砖块飞散；填充墙的存在使得直接作用于下层柱上的冲量明显增加，下层柱发生显著剪切破坏，1层楼板出现严重上拱破坏，其跨中位置上移约165 mm；边梁在结构主要承重构件失效后同样发挥连接作用。

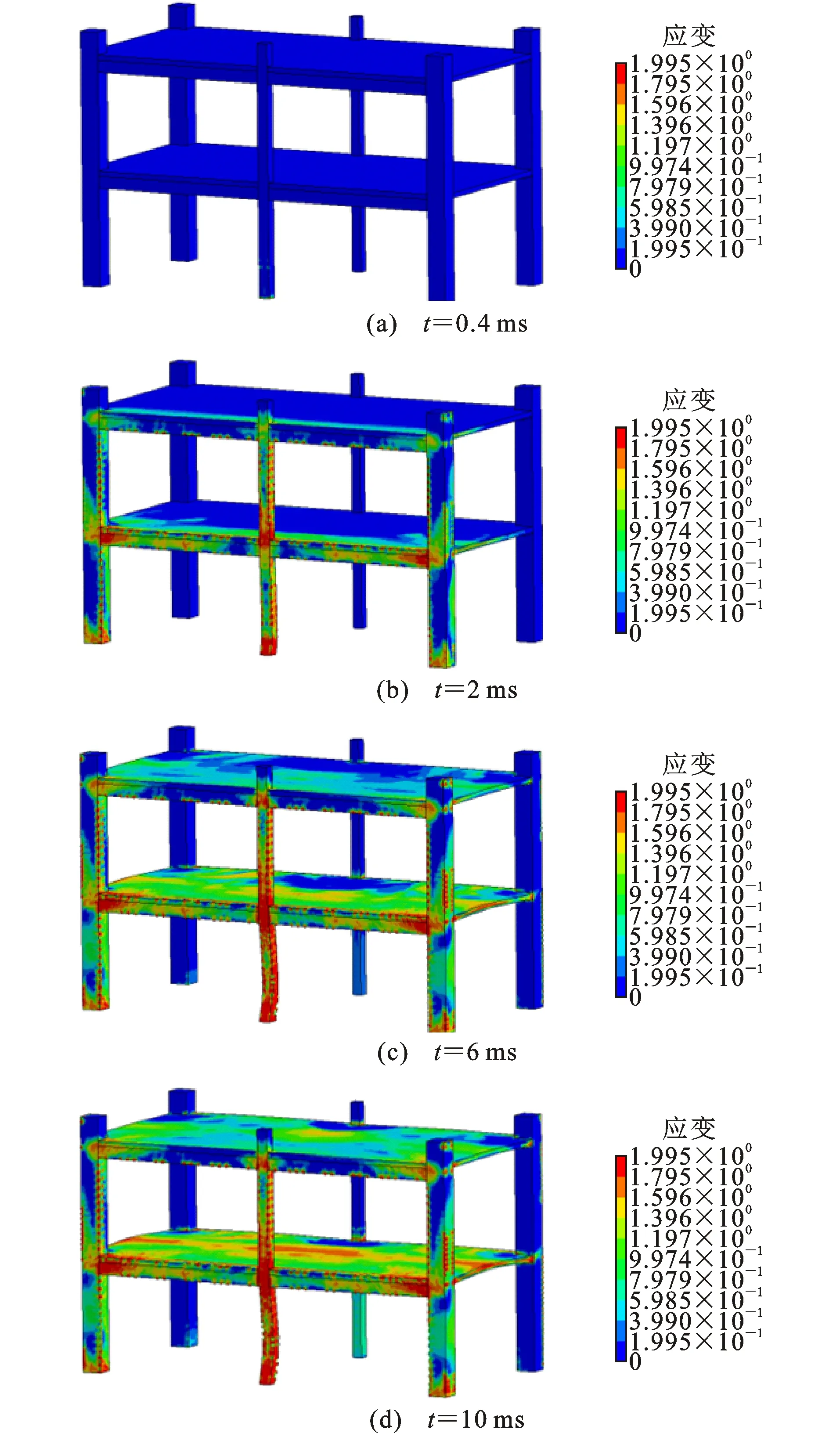
图26 工况4主体结构整体损伤破坏云图Fig.26 Overall Damage Contours of Structure in Scenario 4

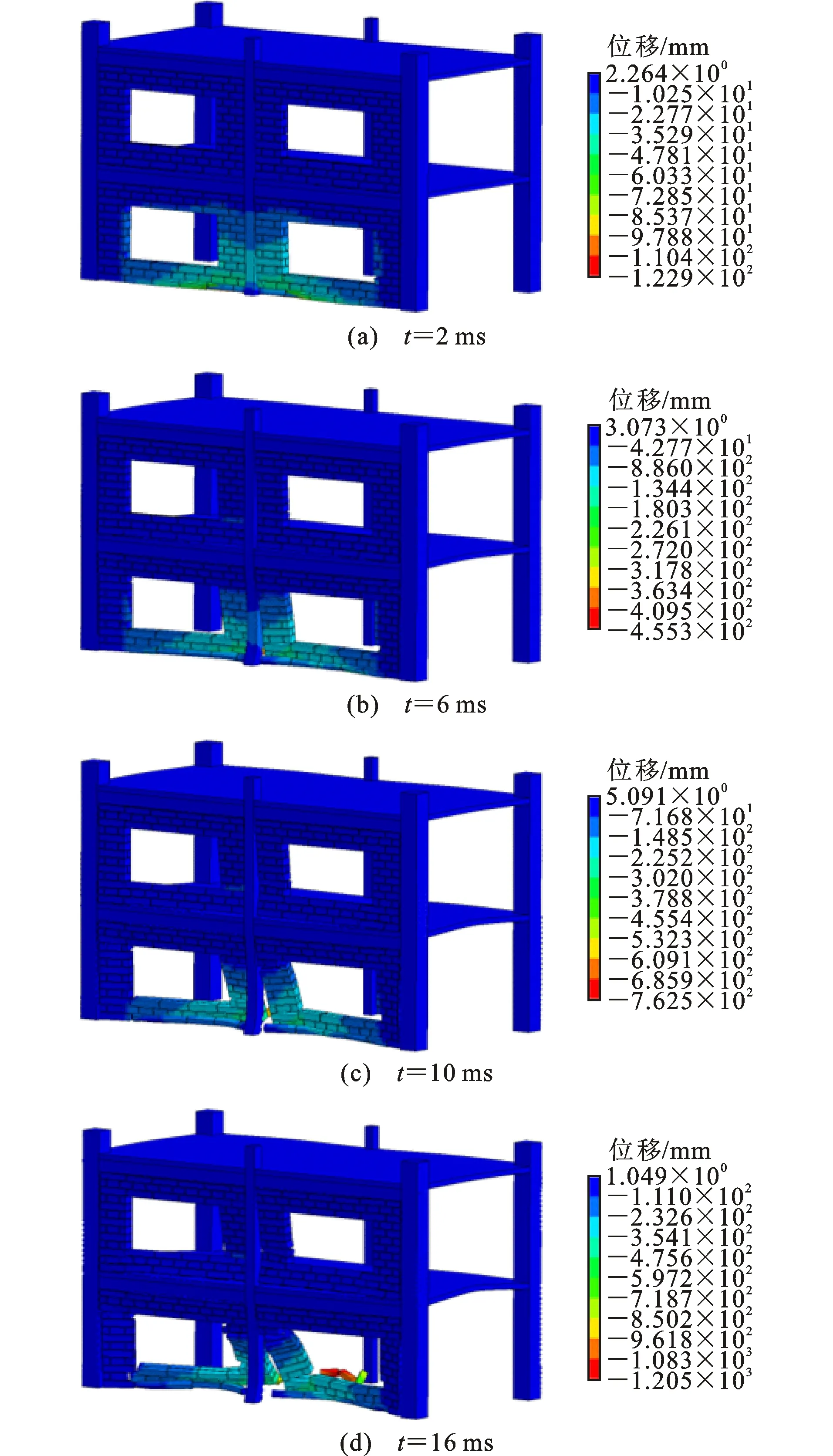
图27 工况4填充墙整体损伤破坏云图Fig.27 Overall Damage Contours of Infilled Wall in Scenario 4

3.5 工况5车库

3.5.1 工况5超压时程

图28为工况5不同时刻爆炸冲击波传播云图。爆炸冲击波在传播过程中，部分在结构底层区域发生反射、绕射并不断向前传播，其余部分在二层填充墙位置发生反射。

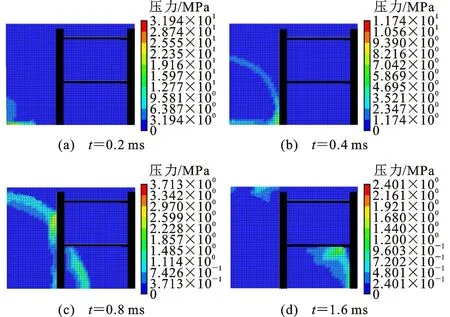
图28 工况5不同时刻冲击波传播云图Fig.28 Propagation Contours of Blast Waves at Different Instants in Scenario 5

图29为工况5试验和数值模拟的正面反射超压结果。可以发现：中柱正面超压模拟值均小于试验值，仅F3测点的模拟结果误差较小。背面超压传感器均在试验中被破坏，相应测量值失真，而超压模拟值沿高度分布较为均匀，最大值为0.4 MPa。

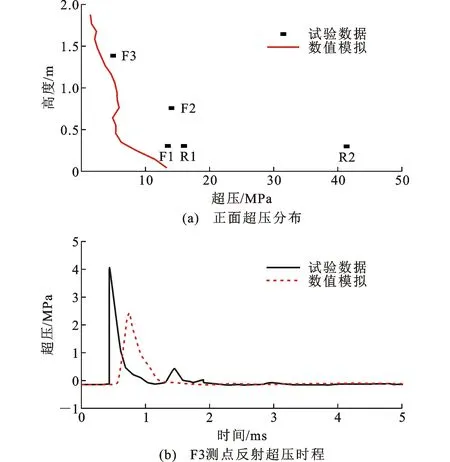
图29 工况5试验和数值模拟的正面反射超压结果对比Fig.29 Comparisons of Reflected Overpressure in Front of Column Between Experiment and Numerical Simulation in Scenario 5

3.5.2 工况5冲量时程

图30对比了工况5试验和数值模拟的框架中柱正面冲量沿高度方向分布情况。可以看出：数值模型较好地模拟了中柱正面冲量分布情况，对应测点相对误差小于5%，正面冲量在地面附近呈明显梯度分布；由于二层填充墙较大程度阻隔了爆炸冲击波的传播，下层柱背面冲量模拟值在对应位置出现骤降。

3.5.3 工况5结构响应

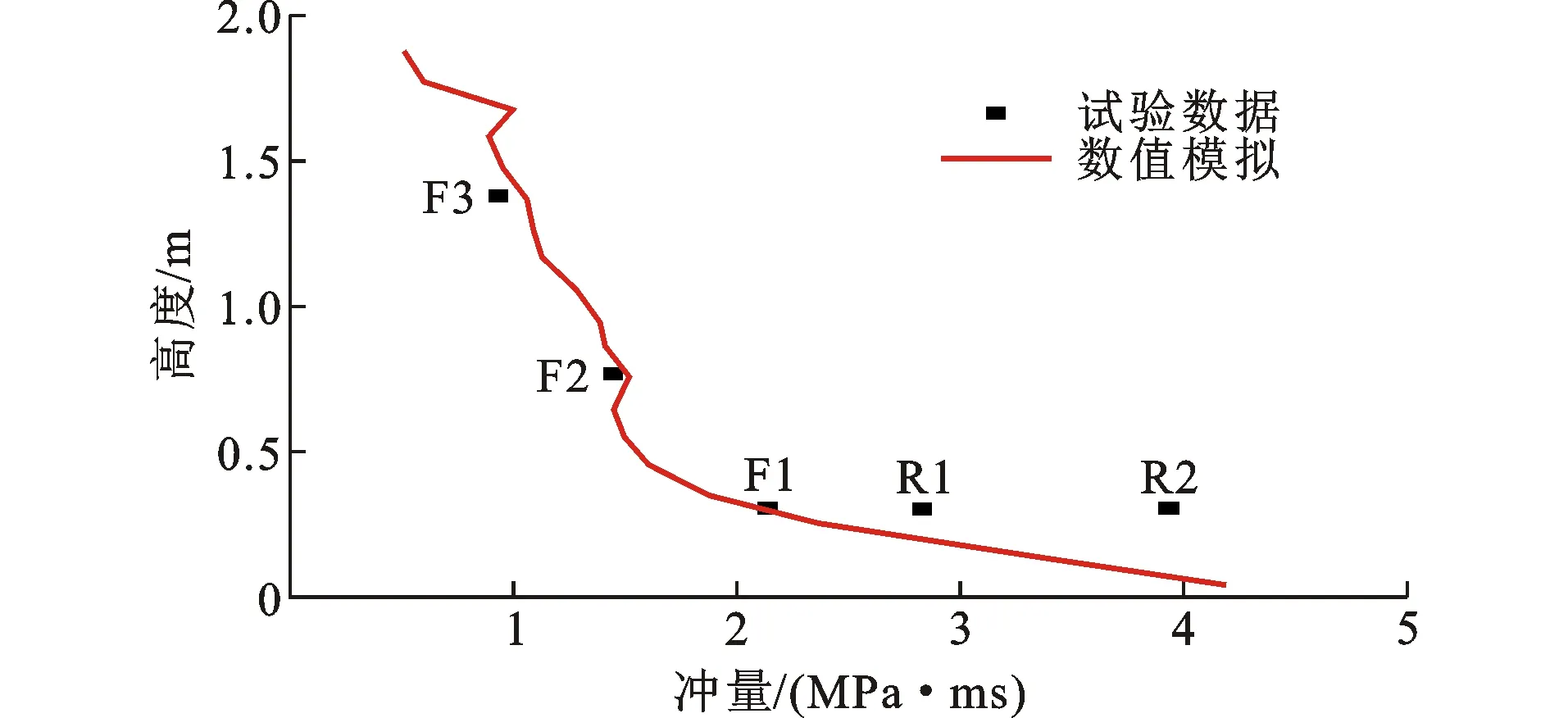
图30 工况5试验和数值模拟的正面冲量沿高度方向分布对比Fig.30 Comparisons of Impulse Distributions in Front of Column Along Column Height Between Experiment and Numerical Simulation in Scenario 5

图31对比了工况5局部构件损伤破坏。由于填充墙设置不同，爆炸冲击波在下层柱位置发生绕射，相应变形较小，而冲击波在上层柱位置发生反射，相应变形较大，但模拟超压存在临近地面部分较大、沿高度方向衰减较快等问题，模拟得到下层柱底部变形偏大并出现剪切破坏，二层柱整体变形较小；相较于其余4组工况，一层楼板上下表面压力差最大，其上拱破坏最为严重，跨中位置上移203 mm，托板连接位置同样出现严重变形。

图32、33分别为工况5填充墙和主体结构损伤破坏云图。爆炸冲击波首先使下层柱及结构连接处出现变形，同时二层填充墙发生剪切破坏，上层柱变形明显增加；一层楼板严重上拱破坏，二层楼板无明显变形；边梁同样在结构主要承重构件失效后发挥连接作用。

本文数值模拟结果汇总如表3所示。

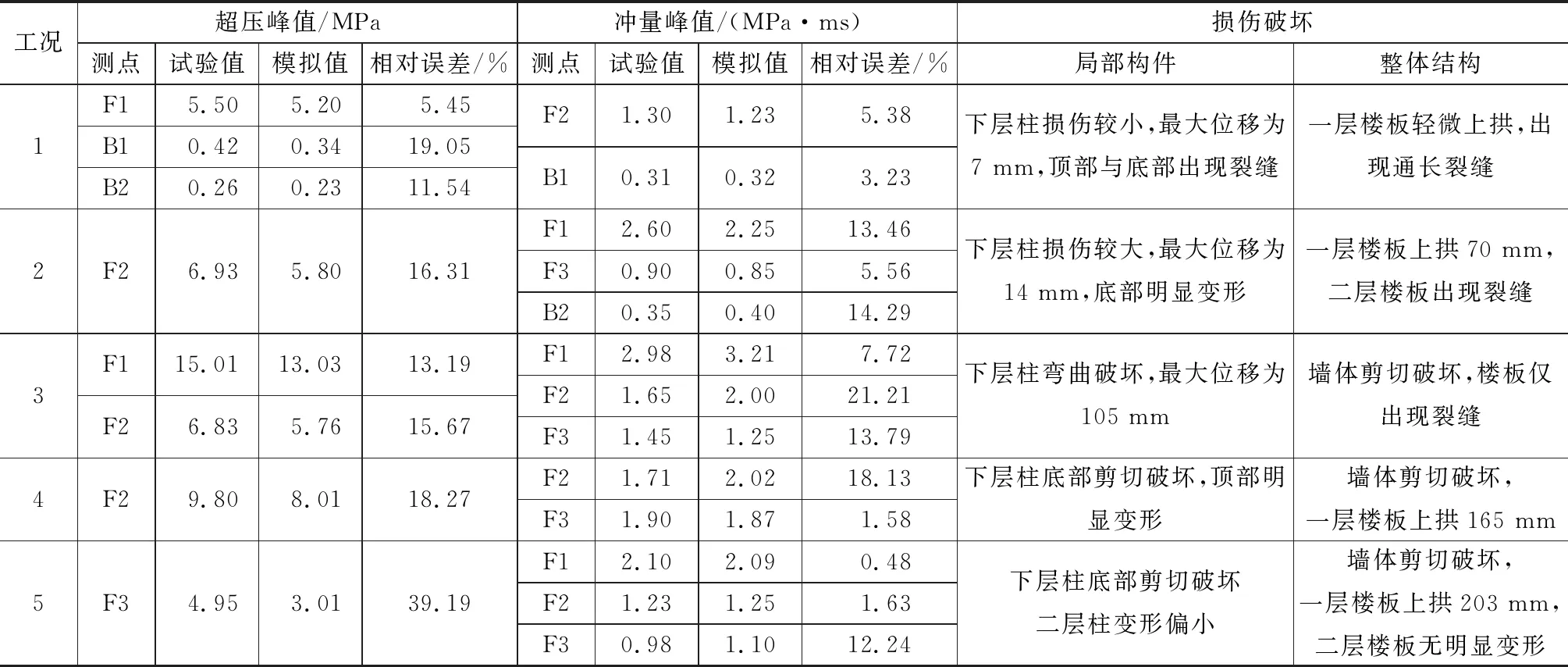
表3 数值模拟结果Table 3 Numerical Simulation Results

图31 工况5试验和数值模拟的局部构件损伤破坏对比Fig.31 Comparisons of Damage of Local Component Between Experiment and Numerical Simulation in Scenario 5

4 结 语

(1)当空气、炸药网格尺寸为50 mm×50 mm时，有限元模型可以较好地预测爆炸冲击波的传播过程，包括冲击波在地面和结构的绕射、反射和透射现象及其与结构耦合作用过程。

(2)框架中柱的正面反射超压模拟值呈上小下大的梯度分布。

(3)框架中柱的冲量模拟值和试验值较为吻合，正面冲量呈上小下大的梯度分布，背面冲量在楼层位置和砖墙附近明显增大。

(4)底层框架中柱的损伤破坏与试验接近，其跨中位移模拟值和试验值相对误差小于5%。

(5)填充墙能够显著增加中柱位置的冲击荷载，导致构件变形失效；填充墙可以阻止爆炸冲击波在结构内部传播，但同时会增大底层楼板上下表面压力差，引发楼板严重上拱破坏。

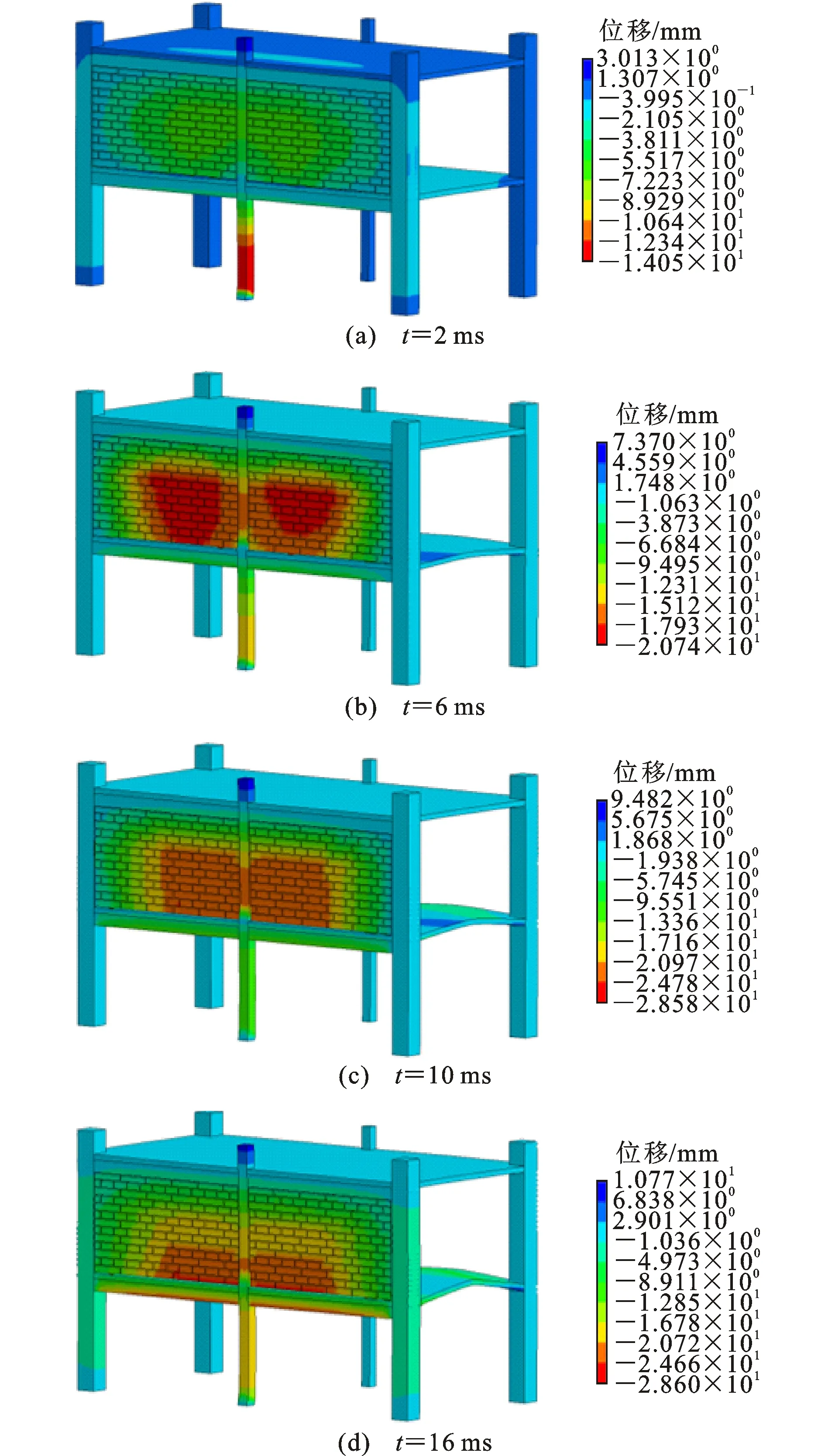
图32 工况5填充墙整体损伤破坏云图Fig.32 Overall Damage Contours of Infilled Wall in Scenario 5

图33 工况5结构整体损伤破坏云图Fig.33 Overall Damage Contours of Structure in Scenario 5

(6)通过数值模拟和试验数据对比，验证了本文采用的数值模拟方法、网格尺寸、材料模型与参数取值的正确性与适用性，可为原型RC框架结构的抗爆响应和破坏倒塌分析提供有益的参考。