基于Kalman滤波技术的超高频变换器稳态特性分析
江心怡,陈艳峰
(华南理工大学 电力学院,广东 广州 510641)
2021年3月,全球能源互联网发展合作组织对外发布了中国碳达峰、碳中和系列研究报告。其中,据《中国2030年能源电力发展规划研究及2060年展望》预测, 2025—2030年新增电力需求将全部由清洁能源满足,清洁能源装机占比将大幅增加,光伏发电作为新能源发电中的重要组成,势必会得到大力发展[1]。
目前,光伏发电多需要采用电力电子器件进行升降压变换,而电力电子器件正沿着高频化、小型化的趋势发展。频率的升高将导致变换器的损耗增加,进而影响变换器的工作效率[2-3]。超高频(very high frequency, VHF)变换器工作频率高,其开关元件均利用软开关技术以减小功率损耗,且可以选用更小的电感、电容作为主电路元件,有效减小变换器的体积,提高功率密度[4];同时,VHF变换器在周期时间内传输与储存的能量减小,使瞬态响应速度得到提升[5-7]。目前已将VHF变换器应用到LED驱动系统、VRM(电压调节模块)、无线电力传输等领域[8],若将其应用于光伏发电,必将有利于提升光伏发电的效率。
虽然VHF变换器优点众多,但电路中存在较多的未知杂散参数,使系统对谐振点变化的敏感度较高,同时也会影响系统的工作效率,为此需要在存在未知偏差的情况下,对VHF变换器建立合理的数学模型,使其在受到干扰参数变化的情况下仍能保持较好的稳态特性。目前常见的建模方法有状态空间平均法[9-11]、扩展描述函数法[12]、离散映射建模法[13-14],其中:状态空间平均法无法适应超高的工作频率,无法描述VHF变换器中各状态变量的谐振变化规律,仅能描绘变换器的宏观变化趋势;扩展描述函数法虽然能够描述各状态变量的变化,但较为复杂且计算量极大,不利于扩展至各类型的变换器中;离散映射建模法需要明确状态变量在每个模态的初始状态,而工作在软开关模式的VHF变换器工作模态较多,且每个模态的初始条件难以确定。因此,亟待解决VHF变换器的数学建模问题。Kalman滤波技术采用最优估算理论,能够使采集的信息与其相应真实值的误差的方差最小[15-16],常被用于跟踪含有干扰的信号。将Kalman滤波器用于VHF变换器的数值建模[17],不仅能实现信号的有效预测,且具有计算量小的优点。
本文对VHF Boost谐振变换器进行模态分析,并结合电路要求合理设计电路元件参数;随后采用Kalman滤波技术进行数值建模;最后进行稳态特性分析,验证Kalman滤波技术在VHF变换器中的适用性,为后续研究变换器动力学特性提供思路。
1 VHF Boost谐振变换器电路拓扑
典型的VHF Boost谐振变换器原理电路如图1所示,由前级Φ2类逆变器和后级E类电压型整流器级联而成。前级电路包含电感LF、LM,开关管ST,电容CF、CM、CF;r1和r2分别为LF和LM的寄生电阻,CF的值包括ST的寄生电容,若寄生电容的大小能够满足电路设计要求,可无需外加并联电容。后级电路包含电感Lr,电容Cr、Co,二极管SD和负载R;Lr的寄生电阻为r3,输出电容Co足够大,可将输出电压视为恒定值Uo。为了简化分析过程,忽略其他储能元件的寄生参数。
1.1 变换器的模态分析
根据ST和SD的开关状态,系统在一个开关周期内可分为以下4种工作模态。4种工作模态对应的等效电路如图2所示,其中:D1、D2分别为开关管ST、二极管SD的占空比,而D3和D4应满足D1+D2+D3-D4=1的条件,为相关工作模态的占空比,fs为工作频率。
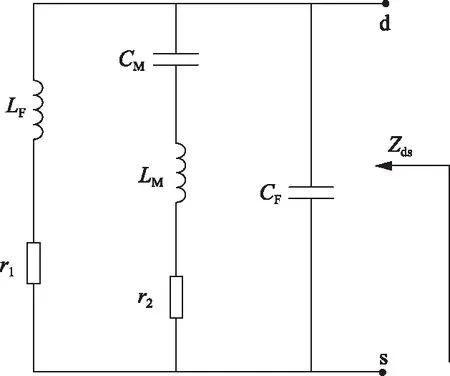
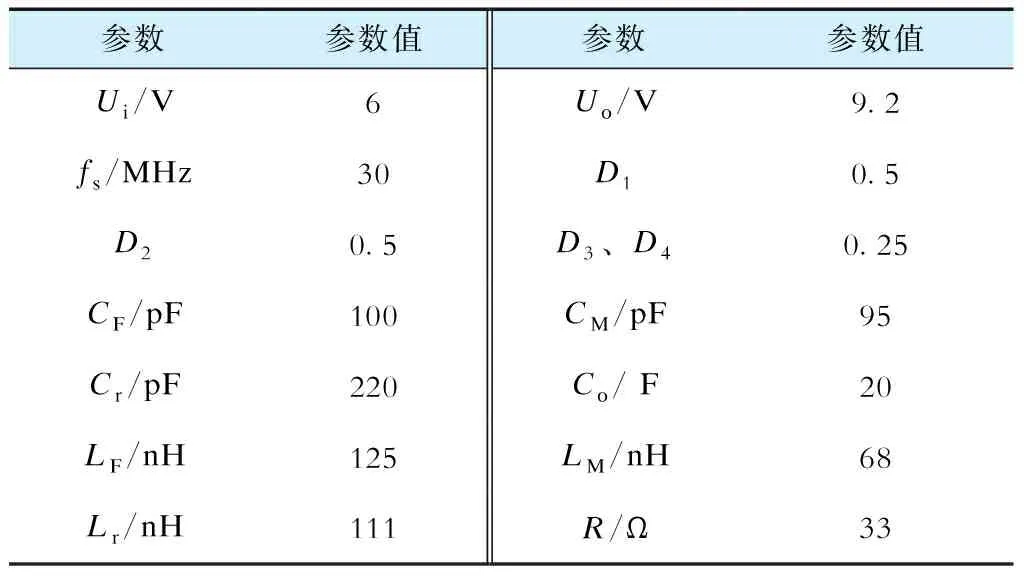
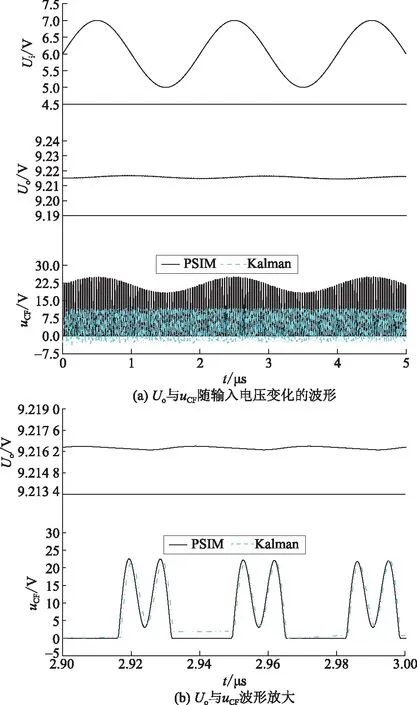
a) 模态1 (0≤t (1) 图1 VHF Boost 谐振变换器的电路拓扑图[18]Fig.1 Circuit topology of VHF Boost resonant converter [18] 图2 VHF Boost谐振变换器的工作模态Fig.2 Working mode of VHF Boost resonant converter b) 模态2 (D4Ts≤t (2) c) 模态3 (D1Ts≤t<(D1+D3)Ts),等效电路如图2(c)所示。此时:ST与SD均关断;CF、CM、Cr、LF、LM和Lr之间发生多级谐振,因此电流iLF、iLM、iLr和电压uCF、uCM、uCr均按准正弦规律变化,直到t=(D1+D3)Ts时刻,uCr增大至输出电压Uo,二极管SD由于受正向偏置电压而导通,该模态结束。此阶段的系统状态方程为: (3) d) 模态4 ((D1+D3)Ts≤t (4) 若VHF Boost谐振变换器的工作频率为fs,根据变换器的工作原理[18-19],由Cr和Lr组成的谐振回路的频率为fs,由CM和LM构成的谐振回路的频率为2fs。因此,各谐振单元的工作角频率ωs应满足: (5) 式中ωs=2πfs。因此,在确定工作频率的情况下,Lr的取值可以由Cr唯一确定。Φ2类逆变器的阻抗网络如图3所示,Zds为其等效阻抗。根据Φ2类放大器的工作原理,Zds的2个极点分别为ωs和3ωs[19],因此LF、LM和CM的值可以根据确定的CF和fs求解,如式(6)所示。 图3 Φ2类逆变器的等效电路Fig.3 Equivalent circuit of class Φ2 inverter (6) 开关管ST的占空比可以由驱动电压uGS控制,可设占空比D1=0.5。根据变换器的模态分析,电容Cr两端电压uCr在D1Ts时刻谐振至零点,且在D4Ts时刻满足电容电压不突变,因此可得uCr应满足以下条件: (7) 输出电压纹波可近似计算为: (8) 纹波分量小,且输出电容Co≫Cr,因此可以近似计算出D2=0.5。各占空比之间存在D1+D2+D3-D4=1的代数关系,结合D1、D2的值带入式(7),可以最终确定D3=D4=0.25。 利用电感Lr的能量传递过程计算输出电压Uo。即在模态1时Lr向输出端放电,iLr线性减小;当开关管ST关断时,电路发生频率为fs和3fs的多级谐振,因此Lr在反向充电完毕后,经时间t=(1-D1)Ts/3将能量传输给输出端,故输出电压 (9) 根据上述理论设计,得到变换器的各个参数,见表1。 表1 VHF Boost变换器各参数设定值Tab.1 Setting values of VHF Boost converter parameters 根据电路的工作过程,可以用理想的开关函数δ(q)(t) (q=1,2)来描述ST和SD的占空比。定义开关函数: (10) (11) 利用开关函数,可将分段微分方程式(1)—(4)整理为统一的状态微分方程: (12) 矩阵A、B表达式如下: Kalman滤波技术通过加入观测扰动,求得采集的信息与其真实值的误差,利用最优估算理论,求得误差的最小方差来实现信号的有效预测,以提高建模的精确度。因此在建立等效数学模型时,还需要分析观测值与真实值之间的关系: Y=HX+V. (13) 式中:H为观测矩阵,此次需要对全部状态变量进行观测,因此H为6阶单位矩阵;Y为状态变量X的观测值,由状态变量X与观测误差V组成,V一般设定为均值为0,方差为R,设R=diag[0.1 0.1 0.1 1 1 1]。 因此,式(12)、(13)共同构成了基于Kalman滤波技术的等效微分方程组[20]。对式(12)、( 13)进行离散化处理,得到[21]: (14) 式中:h为步长;k表示第k个采样点。设步长h=16.7 ps,Kalman滤波器的迭代过程如下[22-23]。 (15) (16) (17) 反复迭代上述计算过程,可以得到各状态变量的数值解,利用描点法得到相应波形图。同时利用PSIM软件进行电路仿真,得到相应波形图。利用Kalman滤波技术得到的波形与仿真波形的比较如图4所示。 利用MATLAB的拟合工具包,得到各状态变量的表达式,如下(τ=ws(t)): iLF=0.504 8cosτ-0.112 8sinτ-0.056 4cos 2τ+ 0.009 3sin 2τ+0.091 4cos 3τ+0.038 0sin 3τ+ 0.028 6cos 4τ-0.049 6sin 4τ-0.008 6cos 5τ- 0.009 3sin 5τ+0.246 5, (18) iLM=-0.203 5cosτ-0.025 4sinτ+0.035 2cos 2τ+ 0.332 2sin 2τ+0.206 7cos 3τ+0.079 0sin 3τ+ 0.052 3cos 4τ-0.097 4sin 4τ-0.014 7cos 5τ- 0.012 9sin 5τ-0.002 2, (19) iLr=0.504 8cosτ-0.112 8sinτ-0.056 4cos 2τ+ 0.009 3sin 2τ+0.091 4cos 3τ+0.038sin 3τ+ 0.028 6cos 4τ-0.049 6sin 4τ-0.008 6cos 5τ- 0.009 3sin 5τ+0.246 5, (20) uCF=1.173cosτ-7.758sinτ+0.041 8cos 2τ+ 0.019sin 2τ+1.846cos 3τ-4.794sin 3τ- 4.142cos 4τ-2.218sin 4τ-0.757 6cos 5τ+ 1.033sin 5τ+6.798, (21) 图4 状态变量的波形比较Fig.4 Waveform comparisons of state variables uCM=1.427cosτ-11.27sinτ-9.323cos 2τ+ 0.986 6sin 2τ-1.434cos 3τ+3.82sin 3τ+ 1.369cos 4τ+0.688 1sin 4τ+0.142 8cos 5τ- 0.173 9sin 5τ+6.248, (22) uCr=3.446cosτ+2.434sinτ-0.445 1cos 2τ- 2.596sin 2τ-0.595 8cos 3τ+0.673 8sin 3τ+ 0.160 5cos 4τ+0.211sin 4τ+0.144 9cos 5τ- 0.062 9sin 5τ+6.404. (23) 搭建仿真平台如图5所示,其中开关管与二极管的型号分别为Si7454 与 SS3H10。驱动方式采用谐振驱动电路,利用晶振LTC6905发出30 MHz频率的方波,通过电感电容谐振电路进行电流放大。实验波形如图6所示。 图5 实验平台Fig.5 Experimental platform 图6(a)给出了开关管两端的电压uCF与驱动电压uGS的波形图,电压波形趋势与理论分析及仿真结果相似,uCF的峰值电压约为19.1 V,为输入电压的3.18倍,接近Kalman滤波得到的结果21.3 V,该值比仿真结果略低,主要原因可能是开关管寄生电容的数值与器件厂家提供的数据表有一定偏差,且难以在实验过程中测量,同时,电路中存在 图6 实验波形Fig.6 Experiment waveforms 寄生电阻承担了部分电压,使开关管两端的电压低于理论值;由于开关管阈值电压和密勒电容的影响,驱动电压波形为具有直流偏压的类正弦波,占空比约为50%,符合理论分析的要求。同时测量的驱动电压波形为开关管门极寄生电阻前的电压,与实际的驱动电压存在一定的相位偏差,在示波器中具体表现为驱动电压uGS存在一定的相位滞后。 图6(b) 给出了谐振电容电压uCr与输出电压Uo的电压波形,该波形与理论和仿真得到的结果基本相似,谐振电容电压uCr为9.8 V,与Kalman滤波得到的9.58 V结果相近,两者存在偏差的主要原因为电路中存在寄生电阻。且受限于实验室仪器的精度与元件生产过程中产生的误差,uCr波形与仿真存在一定的波形畸变。输出电压Uo为8.5 V,由于输出整流二极管存在约0.7 V的导通电压降落,因此该结果与理论和仿真得到的结果在误差范围内相符合。 值得注意的是,由于工作频率高,目前无法观察到各支路的电流波形,且实验结果与所提出的方法和仿真结果之间不可避免地存在误差。这是因为一方面由于寄生参数的影响,样机很难在最佳谐振点运行;另一方面,寄生参数延迟了开关器件的开通和关断动作,因此实验电路实际上并没有实现零电压开关。 利用PSIM仿真软件可以对各状态变量进行傅里叶变换,确定状态变量中各谐波分量的比例,如图7所示,各状态变量主要由直流分量、基波分量以及5倍频内的高次谐波分量构成。 图7 各状态变量的频谱分析Fig.7 Spectral analysis of state variables 利用式(18)—(23)计算建模得到的状态变量主分量的大小,与PSIM傅里叶变换结果进行对比,见表2与表3。可以看出,利用Kalman滤波获得的电流电压分量均与PSIM模拟的结果吻合得很好,这意味着利用Kalman滤波得到的近似解足够精确。由于Kalman滤波通过迭代更新得到解,这一过程势必导致一定时延,在图4中表示为一定的相移,但由于数值精确度较高,且相移角度小,在未来闭环设计中考虑相移因素便可以进一步缩小这一缺陷带来的影响。 表2 电流变量的谐波比较Tab.2 Harmonic comparisons of current variables 表3 电压变量的谐波比较Tab.3 Harmonic comparisons of voltage variables 为观测该电路的稳压效果,将一个幅值为1 V、频率为500 kHz的扰动分量引入输入电源中,观测输出电压与开关管两端电压的波形变化。图8(a)所示为输出电压Uo与开关管电压uCF随输入电压变化的波形。在不加入闭环控制时,即使在扰动幅度占输入电压的16%,且电路不存在大容量的滤波电容的情况下,输出电压的电压波动Δv<0.05 V,扰动幅度为输入电压的8‰,开关管电压uCF峰值为25 V,电压波动Δv<3.5 V,说明该电路具有良好的稳压效果,利用本文提出Kalman滤波方法能够实现有效跟踪电压的变化情况。 图8 输入、输出电压波形对比Fig.8 Input and output voltage waveform comparisons 本文首先对含有寄生参数的VHF Boost谐振变换器进行模态分析,并利用近似关系确定各个开关的导通时间,同时选定主电路各储能元件的参数值;其次利用Kalman滤波技术在变换器含有变化干扰参数的情况下保持较好跟踪特性,将滤波计算应用于VHF Boost谐振变换器的建模中,不仅能够实现良好的跟踪特性,而且具有计算量小、操作简单的优点;最后对VHF Boost电路进行稳定性分析,证明该电路具有较好的电压稳定的特点,且利用Kalman滤波进行建模可行性验证。本方法可以推广到其他类型的VHF变换器的建模中,为VHF变换器数学建模与动力学特性研究提供思路。

1.2 变换器的参数设定
2 基于Kalman滤波技术的建模分析

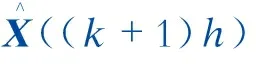

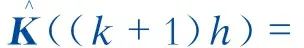

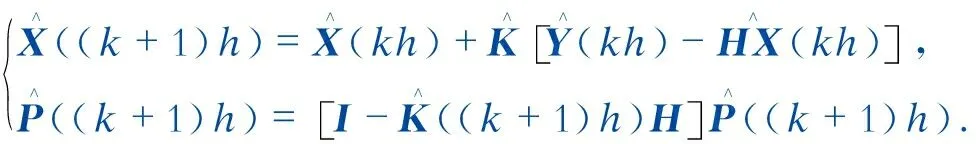
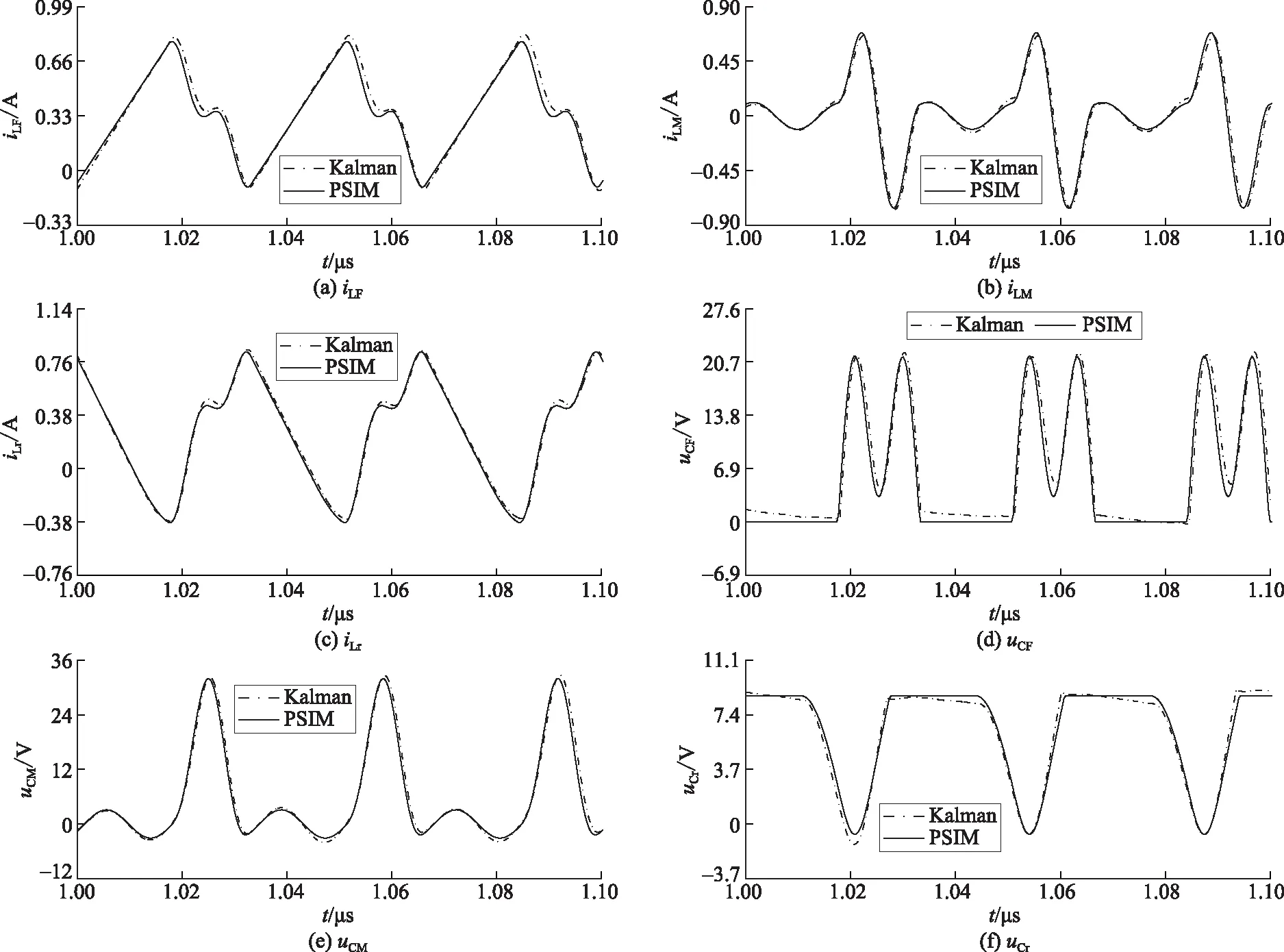


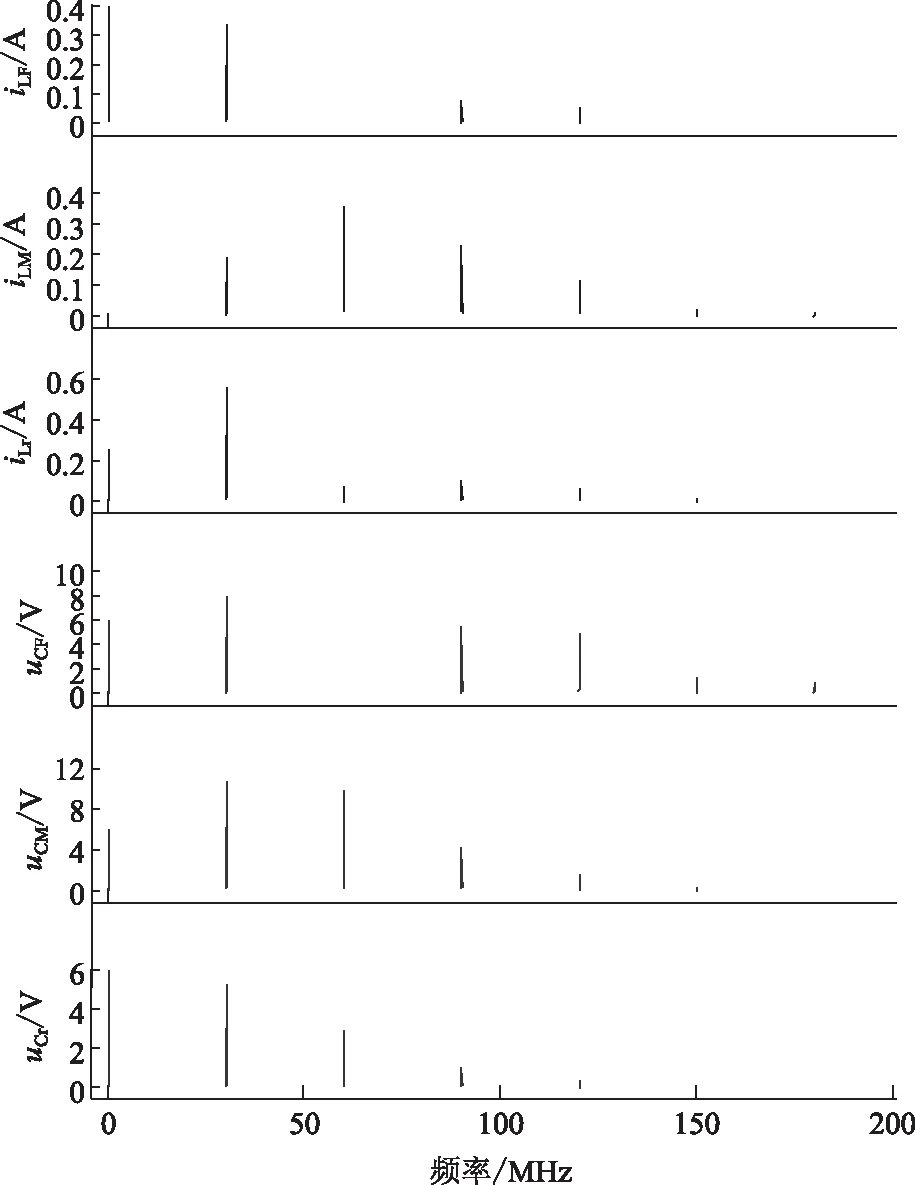
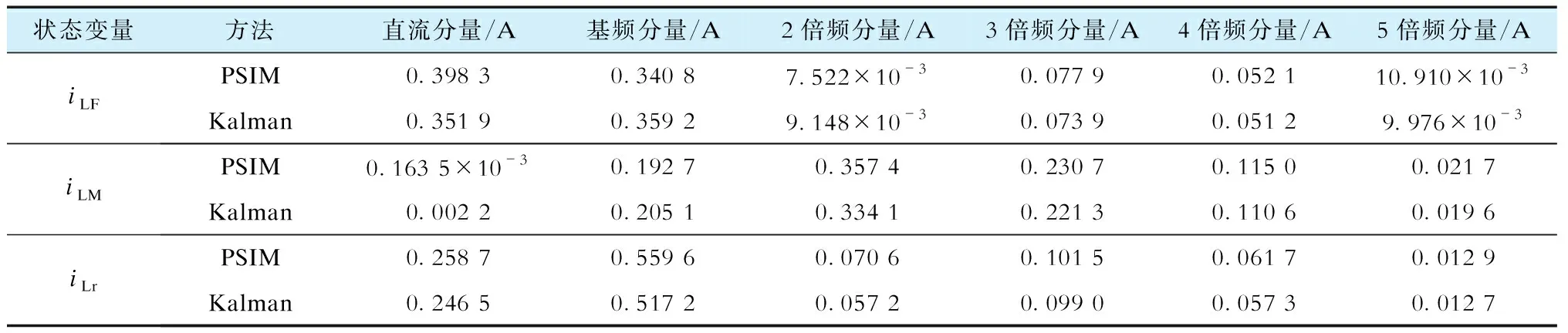
3 稳态特性分析

4 结束语

