高速磁浮U形轨道梁模态试验研究

吴梦笛,李培刚,2,刘 丹,李俊奇,赵 雄,林晓波

(1.上海应用技术大学轨道交通学院,上海 201418； 2.大连理工大学建设工程学部,辽宁大连 116024； 3.长安大学运输工程学院,西安 710064； 4.中铁二十三局集团有限公司,成都 610041)

磁浮交通作为一种无接触式电磁悬浮导向和驱动的轨道交通方式，因具有低噪声、平稳性强、安全性高、节能环保等优势，成为轨道交通发展的一种趋势[1-3]。如图1所示，本文试验磁悬浮轨道梁为中铁二十三局研制的装配式U形磁浮轨道梁，U形轨道梁两侧支撑列车横向受力。该轨道梁相较传统常导电磁悬浮中的T形轨道梁[4]，磁浮列车具有更高的内部空间利用率、安全性和稳定性。磁悬浮悬浮间隙小，一般仅为8 mm[5]，当悬浮控制适应能力较差、列车在静态或低速运行时，悬浮架易产生自激振动与轨道梁自振相耦合，甚至触碰梁体引起轨道梁的振动[6]，轨道梁的振动不仅会对梁体安全产生危害，同时会反向引起运行车辆振动，列车与轨道梁互相激励共振不仅影响轨道梁的安全和稳定性，威胁车辆的平稳运行，甚至造成重大安全事故[7-8]。

为探究轨道梁对车-梁耦合振动的影响，胡义等[9]通过实例数值计算，分析了梁纵横振动耦合效应机理，得出耦合振动的频率成分与结构固有频率有关。余华等[10]通过轨道梁刚度对列车行走性能影响分析，证实车-梁耦合振动与轨道梁刚度有关，当固有频率大于Vmax/L时，增加轨道梁刚度不能有效减小耦合振动。韩霄翰等[11]通过轨道梁结构对耦合振动的分析得出，固有频率随轨道梁结构参数改变时能抑制控制器参数引起的高频耦合振动，并且可通过增大阻尼比抑制耦合振动。祁金宝等[12]通过对磁浮道岔车轨耦合振动消减试验，得出通过在轨道梁关键部位增加阻尼器可有效降低振动响应。任晓博等[13]通过梁体和磁浮车辆运行速度仿真分析得出，梁体加速度幅值随车辆运行速度增大而线性增长。可见目前在轨道梁对振动的影响已有一定研究，然而从轨道梁自身振动特性的研究还相对较少，试验资料相对缺乏。本文以不同材料钢筋骨架的U形高速磁浮轨道梁为研究对象，采取试验和仿真模态分析相结合的方式得到轨道梁模态参数[14-15]，根据模态试验结果研究不同材料钢筋骨架磁浮轨道梁的抗冲击振动性能，以期为磁浮轨道梁的性能研究与合理选材提供科学依据。U形磁浮轨道梁横截面见图1。

图1 U形磁浮轨道梁

1 试验概况

1.1 试件

如图2、图3所示，为便于试验的分析与开展，将实际结构简化，试验磁浮轨道梁选取半片U形梁，并按轨道梁实际设计尺寸的1/2长度做试验模型。单片梁长2.88 m，截面尺寸如图3(a)所示，共制作5片磁浮轨道梁。

图2 U形磁浮轨道梁试验钢筋骨架结构与试验模型

图3 磁浮轨道梁尺寸(单位:cm)

如表1所示，5片轨道梁分别采用不同材料复合钢筋骨架，钢筋直径为12 mm，钢筋网间距为100 mm。梁体混凝土浇筑强度等级为C80，在室内覆盖湿制养护，养护完成后进行室内试验。

表1 不同材质钢筋骨架轨道梁

1.2 试验系统与设备

试验测量分析系统由三大部分组成：试验激振系统、响应采集系统、模态分析和处理系统。

如图4所示，其中试验设备与软件包括：3 kg激振力锤，加速度传感器DH1A111E，动态信号采集仪DH5893，模态分析系统SNDAS，自制冲击架及导线、夹具等。

图4 激振与采集系统试验设备

1.3 试验方案

1.3.1 测点布置

实验采用时域模态识别法，数据采集方式为单点激振，多点拾振法。在轨道梁测振表面布置38个加速度拾取点(图3(b))，测定布置原则如下。

(1) 测点采集信号能反映磁浮轨道梁被测面的基本外形和特征。

(2) 轨道梁重点关注部位和薄弱位置多布点，且适当增加布点密度。

(3) 布点分布保持左右对称。

(4) 控制测点总体数量，以减少加速度传感器灵敏度误差对实验采集数据质量的影响。

1.3.2 试验方法

如图5所示，轨道梁静置在水泥凸台上，通过螺栓杆将轨道梁与地面紧固，预紧力为10 kN。试验时使用激振锤从135°高度自由下落冲击，对结构的最不利位置L/5处施加冲击载荷(图3(b))，摆锤质量3 kg，杆件质量1 kg，摆锤端部为圆弧形，冲击圆直径约为8 mm，除去摩擦力，冲击速度按6 m/s计算进行模态试验。锤击时注意每次下落为自由落体，摆锤释放高度与角度保持一致，摆锤与轨道梁接触为瞬时接触，即摆锤给轨道梁的载荷为冲击载荷，否则会影响试验效果与试验数据准确度。每个拾振点间隔敲击3次，间隔时间相同，在间隔内保证数据采集的连续性，同时保证前一次冲击引起的振动衰减完毕。为提高试验数据的准确性，在整个模态试验中需保证试验环境没有噪声等振动干扰。试验使用动态信号采集分析系统采集每次激振时的瞬时载荷和加速度数据信号，采样频率为2 kHz。

图5 轨道梁承载凸台与固定螺栓

2 试验结果与分析

2.1 固有频率和阻尼比分析

将试验测量获取的激振点和拾振点时域数据通过快速傅里叶变换(FFT)从时域变换到频域，通过FRF(Frequency Response Function，FRF频响函数)参数估计法识别出轨道梁的模态参数。轨道梁试验前5阶结果如表2所示。

表2 轨道梁模态试验结果

分析试验结果，不同材料的轨道梁固有频率有所差异。S2号试验梁的前4阶固有频率是5种材质中最低的，尤其1阶固有频率显著低于其他材料轨道梁，仅为27.34 Hz，表明不锈钢复合筋轨道梁的整体抗冲击振动性能较低；S5号试验梁的1阶固有频率最高，为39.37 Hz。S3号试验梁、相比其余4种轨道梁整体固有频率处于较高位置，其3阶及4阶频率远高于其他材料，表明此材料轨道梁的稳定性更好。根据表2试验结果，5种不同材质轨道梁1阶固有频率高低顺序为：S5玄武岩复合筋>S3土工格栅+玄武岩复合筋>S1玻璃纤维复合筋>S4土工格栅+玻璃纤维复合筋>S2不锈钢复合筋。表明5种轨道梁中玄武岩复合筋材质的1阶固有频率最高，抗冲击振动效果最好。

根据国家建筑行业标准，5种结构筋的力学性能强弱顺序为：玄武岩复合筋>玻璃纤维复合筋>不锈钢复合筋；土工格栅+玄武岩复合筋>土工格栅+玻璃纤维复合筋。分析试验结果，本试验中5种不同材质的复合筋抗耦合振动强弱顺序为：S5玄武岩复合筋>S1玻璃纤维复合筋>S2不锈钢复合筋；S3土工格栅+玄武岩复合筋>S4土工格栅+玻璃纤维复合筋。表明轨道梁固有频率与钢筋骨架材质有关，且其大小随着钢筋骨架材料力学性能的增强而提高。

分析本试验结果，5种材质轨道梁的每阶阻尼比大小没有明显差异区分，表明轨道梁阻尼比的大小对钢筋骨架材质的变化不特别敏感。这与文献[20]中不同骨料混凝土对模态阻尼比没有明显影响的结论相吻合。

2.2 MAC模态参数验证

模态置信准则MAC(Modal Assurance Criterion，MAC)用来表示各阶模态振型的相关程度[21]，MAC的值在0～1之间，不同阶的模态振型向量之间的MAC定义式为

(1)

式中,φi与φj为同一模态振型向量的估计。

从式(1)可见：当对角线MAC值接近1，即100%时两者是呈线性相关的，如果为不同被测物的模态振型，MAC值应当接近于0，即两者为互相独立正交。非对角线上的MAC值低于0.3，表示拾振点不存在空间混淆现象，测点布置位置准确，被测物的模态参数较好。

试验结果通过MAC判断轨道梁各阶模态振型向量之间是否线性相关，以验证试验结果的可靠性。MAC判断结果如表3所示。

表3 轨道梁模态MAC结果

对不同材料的轨道梁各阶模态进行MAC计算结果可知，MAC矩阵对角线上的值接近于1，对角线外MAC远小于1，其各阶模态的相关度绝大多数都在30%之内。说明各阶模态具有较高的正交性，拾振点不存在空间混淆现象，本试验采集的各激振点和拾振点信号质量较高，模态试验所识别的模态参数反映了轨道梁真实的模态参数，且具有较高准确性。

3 有限元数值模拟

为验证上述试验结果的正确性和可靠性，利用ABAQUS软件建立轨道梁模型进行模态分析，将试验结果与有限元分析结果进行对比。

3.1 有限元模型的建立

通过ABAQUS分别建立5种不同材料钢筋骨架轨道梁模型，梁长2.88 m，钢筋直径12 mm，钢筋网间距为100 mm，采用C80混凝土，混凝土弹性模量E为3.8×104MPa，泊松比ν为0.2，密度ρ为2 600 kg/m3。通过自由网格划分方式对有限元模型进行网格划分，网格尺寸为100 mm。轨道梁的底面受X、Y、Z三向弹性约束，张宇生等[22]在不同约束条件下磁悬浮道岔主动梁自振研究中得出，在有限元仿真模型中施加刚性约束的模态结果显著大于实测值，而弹性约束下模态分析结果与实测值接近。本文有限元模型在使用不同约束方式中验证了上述文献结论的正确性，因此文中模型所述约束方式采用弹性约束，将轨道板底面通过弹簧连接地面。模型钢筋骨架布置和混凝土有限元模型如图6所示，钢筋参数设置如表4所示。

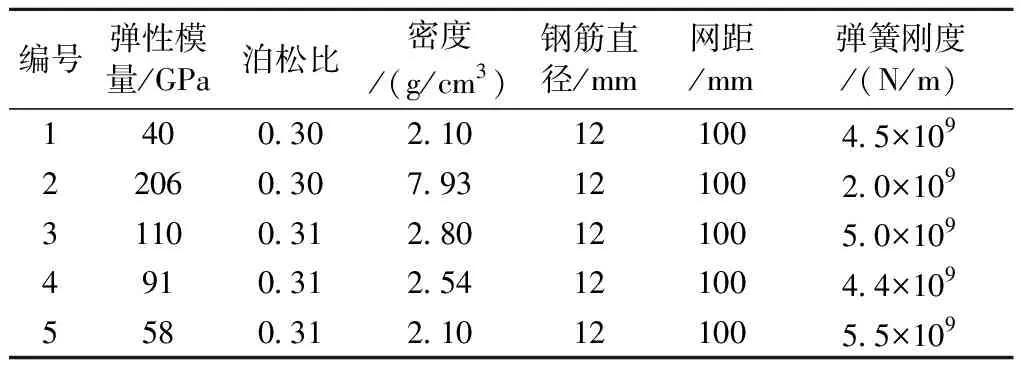
表4 模型钢筋设置参数

3.2 试验结果与有限元分析结果对比

计算有限元仿真分析频率与试验模态固有频率在对应阶次上的差值，通过误差率来判断两者的相关性[23]。

(2)

式中，fA为有限元仿真分析频率，Hz；fT为试验模态固有频率，Hz。

一般情况下，仿真分析模态频率与试验模态频率的误差在10%以内认为两者具有较好的相关性。模型振型如图7所示，因各模型每阶振型特征相近，本文只列出模型1的前5阶振型。

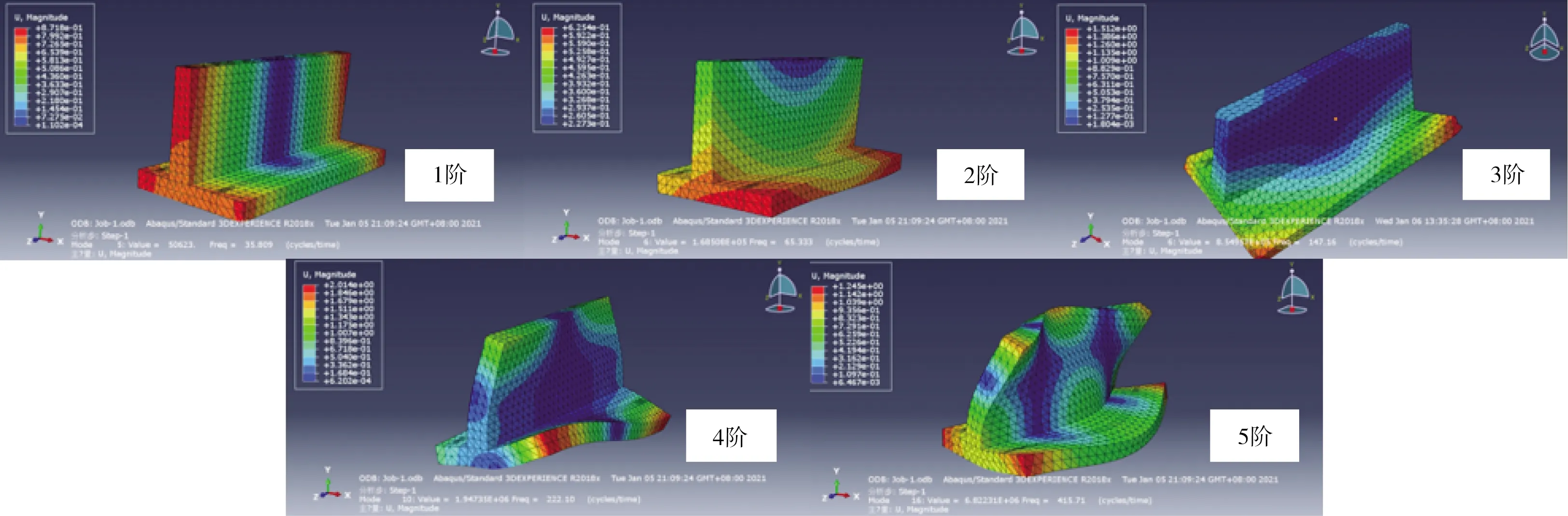
图7 模型1前5阶有限元振型

模态振型分析结果表明，不同材质钢筋骨架轨道梁之间的振型特征差异性不明显，振动形态大体相同。其中1阶为整体横向弯曲振型，2阶为整体垂向弯曲振型，3、4、5阶为扭转振型。

提取各模型的前5阶模态固有频率与试验结果进行对比，对比结果如表5所示。

表5 轨道梁试验与有限元仿真固有频率对比

试验结果的影响因素包括：钢筋骨架实际捆扎和混凝土浇筑与设计的偏差、养护与试验环境、试件锚固预紧力偏差等。S2轨道梁的2阶固有频率与仿真结果偏差较大，结合其余几阶与其他试验梁的对比结果，试验结果总体质量较高，平均误差度低，因此该数据属于正常试验误差。

由表5可知，96%的模态频率误差在10%以内，最大误差为9.8%，最小误差为0.08%，平均误差值为2.57%，在精度允许范围之内。显然，试验与仿真模态分析结果吻合良好，具有一致性。说明了试验结果具有较高的准确性，能够准确反映轨道梁的真实模态参数。

4 结论

以高速磁浮列车U形轨道梁为研究对象，从不同材料的角度研究了轨道梁固有频率和阻尼比差异特性，得到以下结论。

(1)磁浮轨道梁固有频率与钢筋骨架材质有关，且随着钢筋骨架力学性能的增强而提高。

(2)不同材质钢筋骨架轨道梁阻尼比大小没有明显规律与差异区分，表明轨道梁阻尼比大小对浇筑C80混凝土的不同材质钢筋骨架力学性能差异变化不敏感。

(3)不锈钢复合筋轨道梁的前4阶固有频率是5种材质中最低的，表明不锈钢复合筋轨道梁的整体抗冲击振动性能相比较而言最低。

(4)玄武岩+土工格栅材质轨道梁相比其余4种轨道梁各阶固有频率处于较高位置，表明玄武岩+土工格栅材质轨道梁的稳定性相较而言整体抗冲击性能更好。

(5)5片轨道梁的1阶固有频率范围为27.34～39.37 Hz，其高低顺序为：玄武岩复合筋>土工格栅+玄武岩复合筋>玻璃纤维复合筋>土工格栅+玻璃纤维复合筋>不锈钢复合筋。表明5种不同材料轨道梁中相对而言玄武岩复合筋材质的1阶固有频率最高，为39.37 Hz，抗冲击振动效果最好。