分组全连接的近红外光谱定量分析网络

余志荣，洪明坚

重庆大学大数据与软件学院，重庆 401331

引 言

近红外光谱技术是一种高效快速的现代分析技术，具有测量方便、速度快、分析成本低等优点，已成为质量控制、品质分析和在线分析的非接触无损检测的重要手段，并广泛应用于农业生产[1]、食品安全[2]、石油化工[3]等领域。因为近红外光谱具有多重共线性，加上仪器和环境等因素的影响，实际采集的原始光谱中还可能会包含一些噪声信号，所以，在近红外光谱定量分析中需要用到多元校正方法。常用的多元校正方法有：多元线性回归(multiple linear regression, MLR)[4]、主成分回归(principal component regression, PCR)[5]、偏最小二乘(partial least squares, PLS)[6]、支持向量机(support vector machines, SVM)[7]和人工神经网络(artificial neural network, ANN)等。其中MLR，PCR和PLS是线性方法，这类算法容易受到光谱中非线性因素的干扰[8]，而SVM和ANN等非线性方法能克服该问题。

ANN作为一类典型的非线性方法，随着近年来神经网络方法的快速发展，在光谱分析领域中的应用越发广泛。Cui等[9]提出一个卷积神经网络定量分析模型，在3个不同大小的近红外数据集上进行了测试，预测效果优于PLS模型。Wartini Ng等[10]结合可见光、近红外以及中红外光谱，利用卷积神经网络建立土壤多组分同时预测模型，取得了较好的效果。这些神经网络模型的末端通常是由数个全连接层接收前面卷积层提取的特征或原始的样本输入，然后输出预测结果。随着输入维度的增加，全连接层的参数量会变得十分庞大。庞大的参数量使训练时间变长、训练需要的样本量增大、预测效果难以提升。为了降低模型参数量，样本在输入模型之前，通常会用一些降维方法，如主成分分析(principal component analysis, PCA)[11]、小波变换[12]等，或者对输入波长进行选择，如遗传算法(genetic algorithm, GA)[13]、先验知识[14]等，对输入样本进行压缩。这些方法虽已经尽可能地保留样本中的有用信息，但难免还是会丢失一些信息。

针对这一问题，从全连接层的结构入手，提出一种降低全连接层参数量的方法，即分组全连接网络(group fully connected network, GFCN)。该方法直接输入原始的光谱，将原来的全连接层进行分组，用多个局部全连接替代原来的全局全连接。通过在Tecator和IDRC2018数据集上对GFCN进行了验证，并与PLS和FCN算法进行了对比，验证了GFCN的有效性。

1 分组全连接网络

全连接神经网络中，每层的“神经元”和下层的每个神经元之间全互联，神经元之间不存在同层连接，也不存在跨层连接。下层的每个神经元根据权重接受上层网络中每个神经元传递的特征值，经过偏置与激活函数后输出特征值。经过多层特征提取，最终可以得到预期的结果。全连接层的变换过程可以表示为

xFC=A(wx+b)

(1)

A(x)=Relu(x)=max(x, 0)

(2)

其中，w为全连接层的权重，b为偏置项，A(x)为ReLU激活函数，xFC表示全连接层的输出。

然而，全连接层的参数量巨大，且存在冗余。光谱中最主要的特征是吸收峰，吸收峰之间存在间距，波长间隔大的峰不属于同一个吸收峰，所以不需要进行全局的连接来提取特征。结合这一特点，将全连接层内的神经元进行平均分组，同一组内上下层神经元全部互连，不同组神经元之间没有连接，这一结构命名为分组全连接层(group fully connected layer)。分组全连接层的变换过程可以表示为

xGFC=A(w1x1+b1)∪…∪A(wixi+bi),i=1, …,g

(3)

A(x)=Relu(x)=max(x, 0)

(4)

其中，xGFC为分组全连接层的输出，wi为第i组全连接权重，bi为第i组全连接偏置项，g为分组的个数，A(x)为ReLU激活函数。

预测模型的结构如图1所示，将其命名为分组全连接网络(group fully connected network, GFCN)。GFCN可以分为两层：第一层是分组全连接层(GFC)，接收原始的光谱输入；第二层是全连接层(FC)，第一层的输出经过激活函数ReLU后输入到第二层中，然后输出最终的预测值。

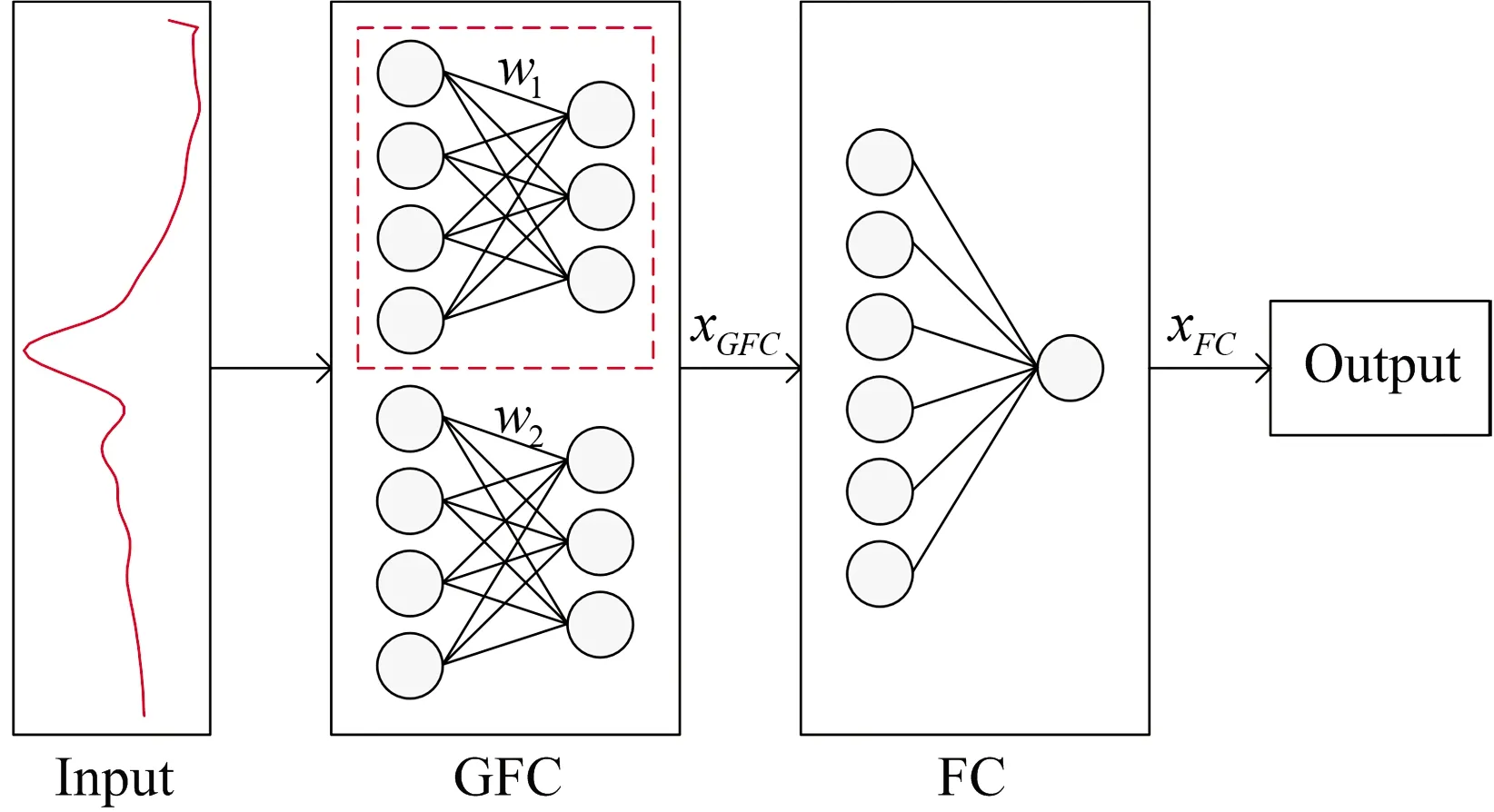
图1 GFCN模型结构图

GFCN在FCN的基础上将传统的全连接层替换为分组全连接层，具有以下的优点：

(1)参数量更少，计算量降低。全连接网络首层的参数量可能占了模型总参数量的一半以上，而且随着光谱样本波长数的增加，参数数量增长迅速。GFCN将第一层的全连接层切分成多个小的全连接层，大幅减少了参数量，计算量也大幅减少。

(2)建模需要的样本数量降低。如果可供训练的样本数量不足，神经网络模型可能会过度学习训练集的样本，导致泛化能力不足，在测试集上效果不佳，也就是进入过拟合状态。一般来说，训练模型需要的样本数量与模型参数量呈正相关关系，GFCN相比FCN，参数大幅减少，需要的样本量也随之降低，这更加适合光谱分析领域中样本较少的情况。

(3)更方便地分析各个波段对预测的贡献。分组后，每组的神经元学习一种特征，不同组之间互不干扰，避免了多组神经元学习同一特征的情况，可以防止模型过度拟合某一波段[15]。同时，每组神经元的输出即是该波段对预测的贡献，不需要再进行复杂的权重计算，方便后续的模型分析。

2 实验部分

2.1 数据来源

Tecator数据集包含215个切碎的肉样品的近红外光谱及对应的水分、脂肪和蛋白质含量，主要目的是预测脂肪含量。近红外光谱是通过TecatorInfratec光谱仪采样得到，波长范围为850～1 050 nm，采样间隔为2 nm，共100个波长。按照数据集原始的划分方法，将样本分成172个训练集样本和43个测试集样本。数据集可从http://lib.stat.cmu.edu/datasets/tecator下载。

IDRC2018数据集来源于IDRC 2018年线下建模竞赛，由于涉及商业信息，数据集的成分信息未公开。IDRC2018共包含200个样本的近红外光谱及未知成分的含量，波数范围5 098～9 989 cm-1，采样间隔为7.71 cm-1，共635个波长。按照数据集原始的划分方法，将样本分成150个训练集样本和50个测试集样本。数据集可从https://www.cnirs.org/content.aspx?page_id=22&club_id=409746&module_id=276203下载。

2.2 数据预处理

为了消除光谱中的基线偏移，提高信噪比，所有的光谱样本都经过Savitzky-Golay平滑(窗口宽度为5，多项式次数为3)和一阶导数处理。处理后的光谱如图2，后续的建模及预测都使用预处理后的数据。

图2 预处理后的光谱

此外，为了加快模型的收敛速度，用于训练FCN和GFCN模型的Tecator数据集还进行了方差归一化处理。IDRC2018数据集各特征的方差差异不大，故不进行归一化。

2.3 模型参数

为了方便对比效果，FCN和GFCN均包括两层隐藏层，两个模型对应层的输出维度均相同。第一层隐藏层输出的长度为输入样本的一半(Tecator数据集为50，IDRC2018数据集为317)，第二层隐藏层的输出为预测值。经过测试，对于Tecator数据集，GFCN的分组数量g设为5；对于IDRC2018数据集，分组数量g设为9。FCN和GFCN在两个数据集上的参数量见表1，因为FCN第一层的参数量占总参数量的90%以上，所以GFCN的参数量约等于FCN的1/g。

表1 FCN和GFCN的参数量

2.4 模型评价指标

选择的评价指标包括：均方根误差(root mean square error, RMSE)和决定系数(coefficient of determination,R2)。计算公式如式(5)和式(6)

(5)

(6)

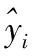
3 结果与讨论

3.1 训练次数及分组数量对模型的影响

训练的轮次对神经网络模型的预测效果至关重要，为探究最优的训练轮次，将测试集样本每隔100次输入到模型中，模型的预测效果随训练轮次变化如图3所示，其中RMSEC是训练集的均方根误差，RMSEP是测试集的均方根误差。可以看到，FCN在迭代10 000次以后，RMSEP基本不再变化，而RMSEC一直下降，出现过拟合现象。GFCN在17 000次左右，RMSEP达到最低点，随后同样出现过拟合现象。因此，为防止出现过拟合现象，FCN模型的训练轮次上限定为10 000次，GFCN定为17 000次。

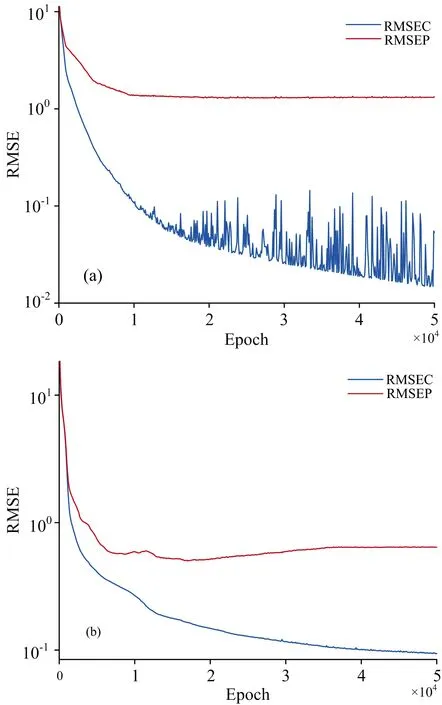
图3 神经网络模型的训练损失和测试损失

为探究分组数量g对GFCN的影响，使用Tecator和IDRC2018数据集分别进行了不同分组数量的实验，模型的预测效果随分组数量变化曲线如图4所示。由于Tecator数据集的波长数较少，只验证了分组个数从1到10的模型性能变化。当分组个数为1时，GFCN等价于FCN。可以看到，当分组个数分别为5和9的时候，GFCN在Tecator和IDRC2018数据集上的效果最好。因此，在后续的实验中，对于这两个数据集，GFCN的分组数量分别设为5和9。

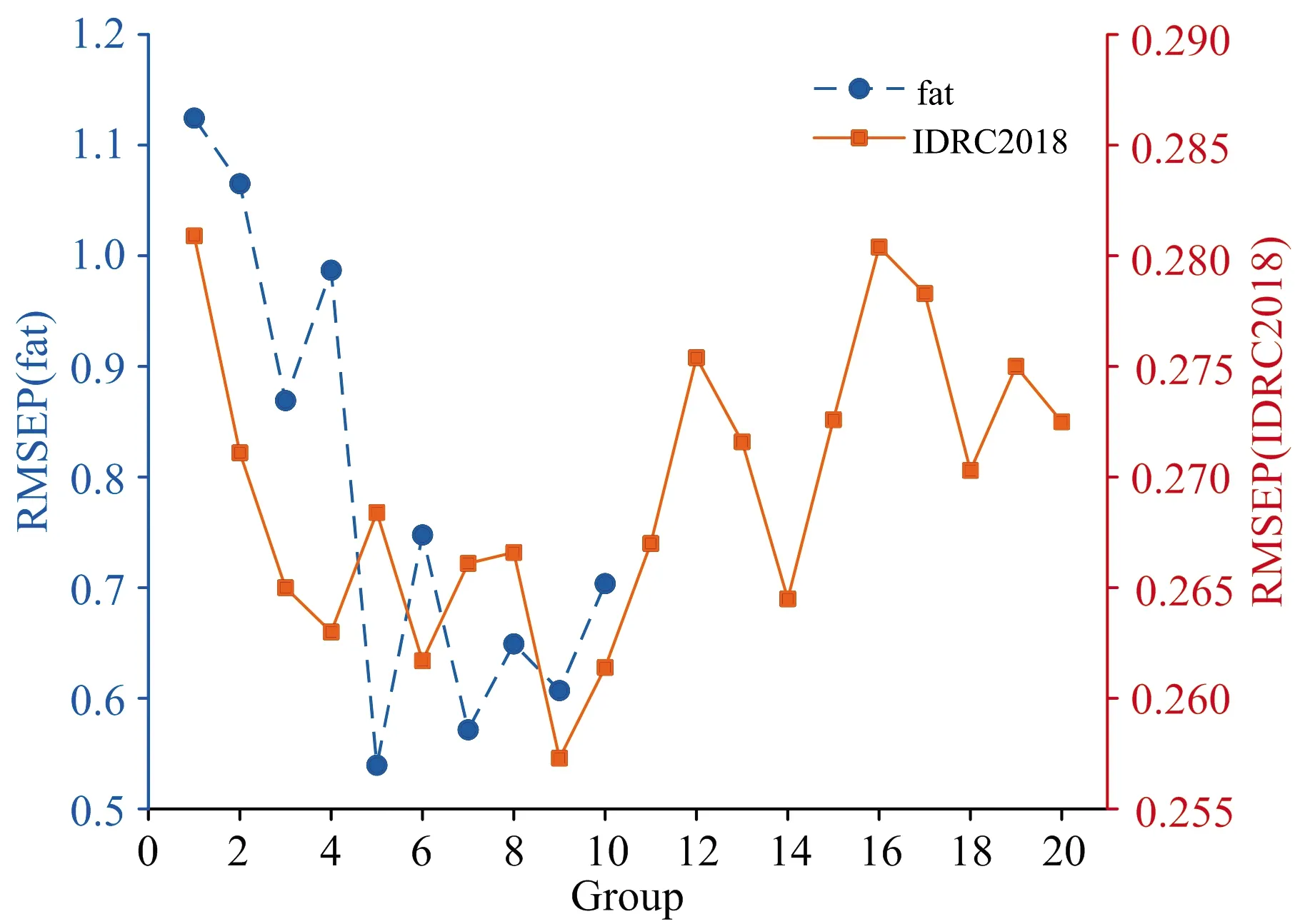
图4 分组数量对GFCN模型预测效果的影响

3.2 不同模型性能比较

为了衡量GFCN的预测性能，选择了目前较为常用的偏最小二乘(PLS)模型以及全连接网络(FCN)作为对比。PLS模型的主成分个数(PC)通过交叉验证方法来选择。三种模型的预测效果如表2所示。结果表明，Tecator数据集的三种成分和IDRC2018数据集，GFCN的预测效果均优于PLS和FCN。

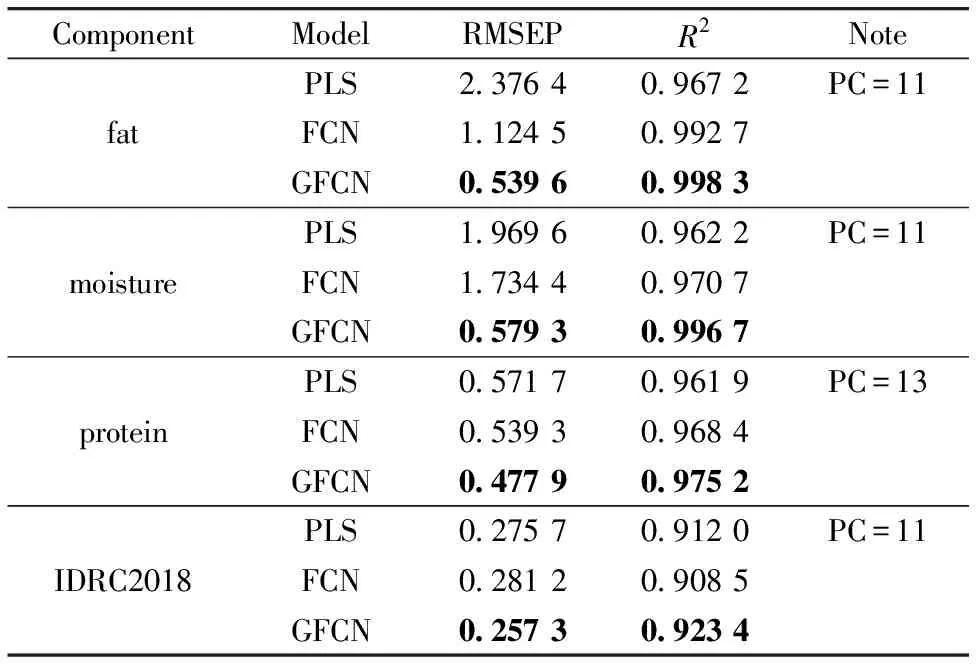
表2 三种模型的预测效果对比

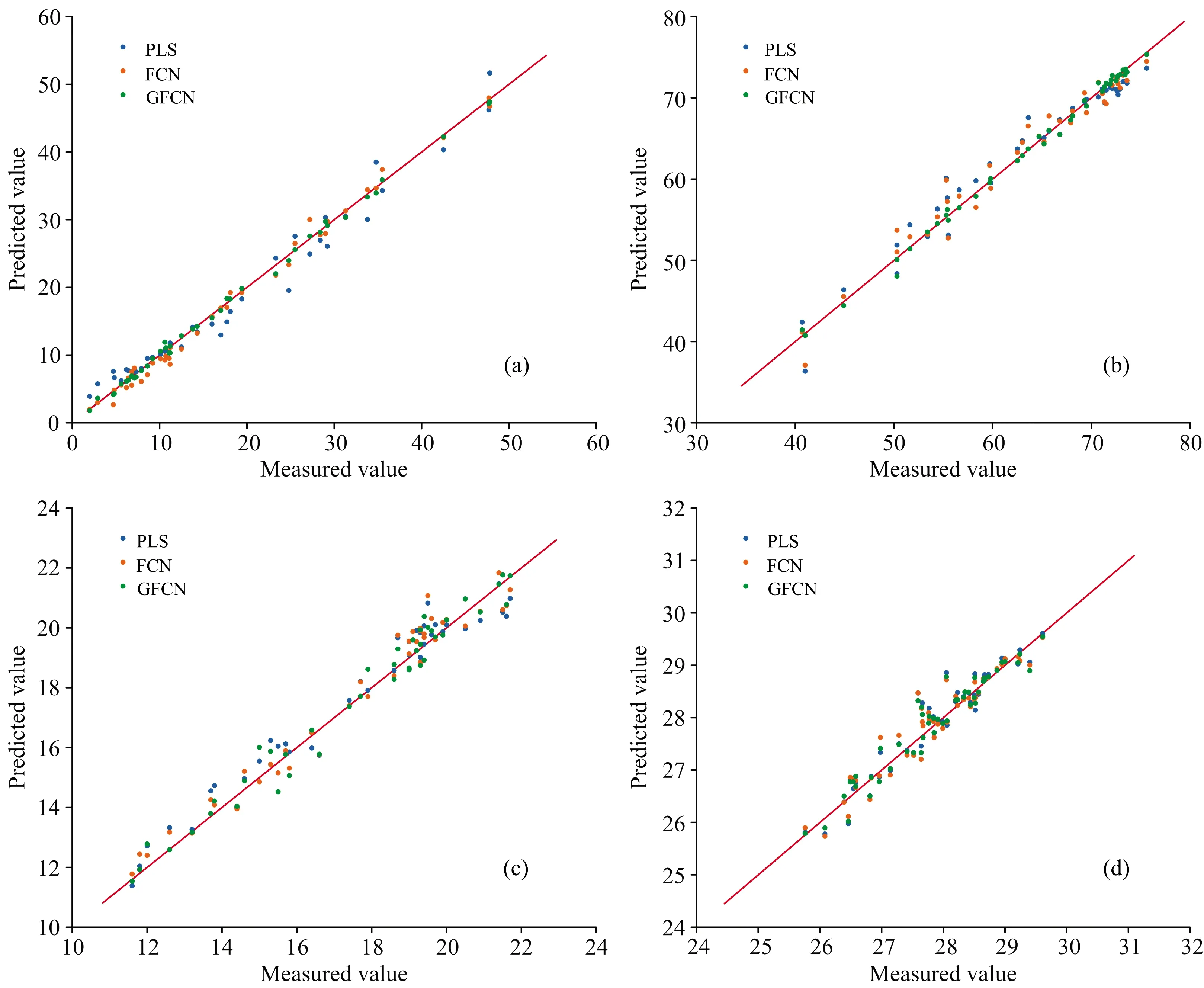
图5 三种模型的预测结果

3.3 训练集大小对模型的影响

为了验证模型在样本数量较少的情况下的建模效果，将Tecator数据集的训练集用Duplex算法选出一部分来训练模型，数量为原数据集的80%～20%。测试集的样本不变，占原数据集的20%。随着训练集的样本数目变化，模型的预测效果如图6所示。PLS模型的总体变化不算太大，预测效果随着样本数目减少有一定的波动。FCN模型的预测效果随训练样本减少急剧下降，而GFCN模型在80%～50%样本的效果变化较小，随后预测误差才逐渐增大。总的来说，在不同的训练样本数量上，GFCN模型的效果均优于FCN和PLS模型，表明，相较于PLS和FCN模型，GFCN模型更适用于样本数量较少的场景。

图6 训练集大小对三种模型预测效果的影响

3.4 模型的解释

为了进一步探索模型工作的原理，计算出每个波长对预测的贡献值：

C=β∘s

(7)

β=Wl2Wl1

(8)

其中，C为各波长的贡献值；β为FCN和GFCN的等效回归系数；s为输入的光谱样本；∘为逐项积运算，即对位元素相乘；Wl1和Wl2为FCN和GFCN第一层和第二层的权重，由于激活函数的影响，将网络第一层输出负值的神经元对应的Wl2权重手动置0。

由于各样本的预测值存在大小差异，为消除该影响，计算出各波长的贡献值占比

(9)

式(9)中，Ri为波长i在贡献值绝对值之和的占比；n为波长点个数。图7展示了所有测试样本的各波长贡献占比，实线表示所有样本贡献占比的均值。可以看到，对于fat成分，880～925 nm处的贡献占比大幅度提升，850～880和950～1 050 nm处的贡献降低。这与波长选择方法[16-17]得到的重要波长位置是相吻合的，表明GFCN方法的预测是基于与目标成分高度相关的波长点，预测结果比FCN更具可解释性。

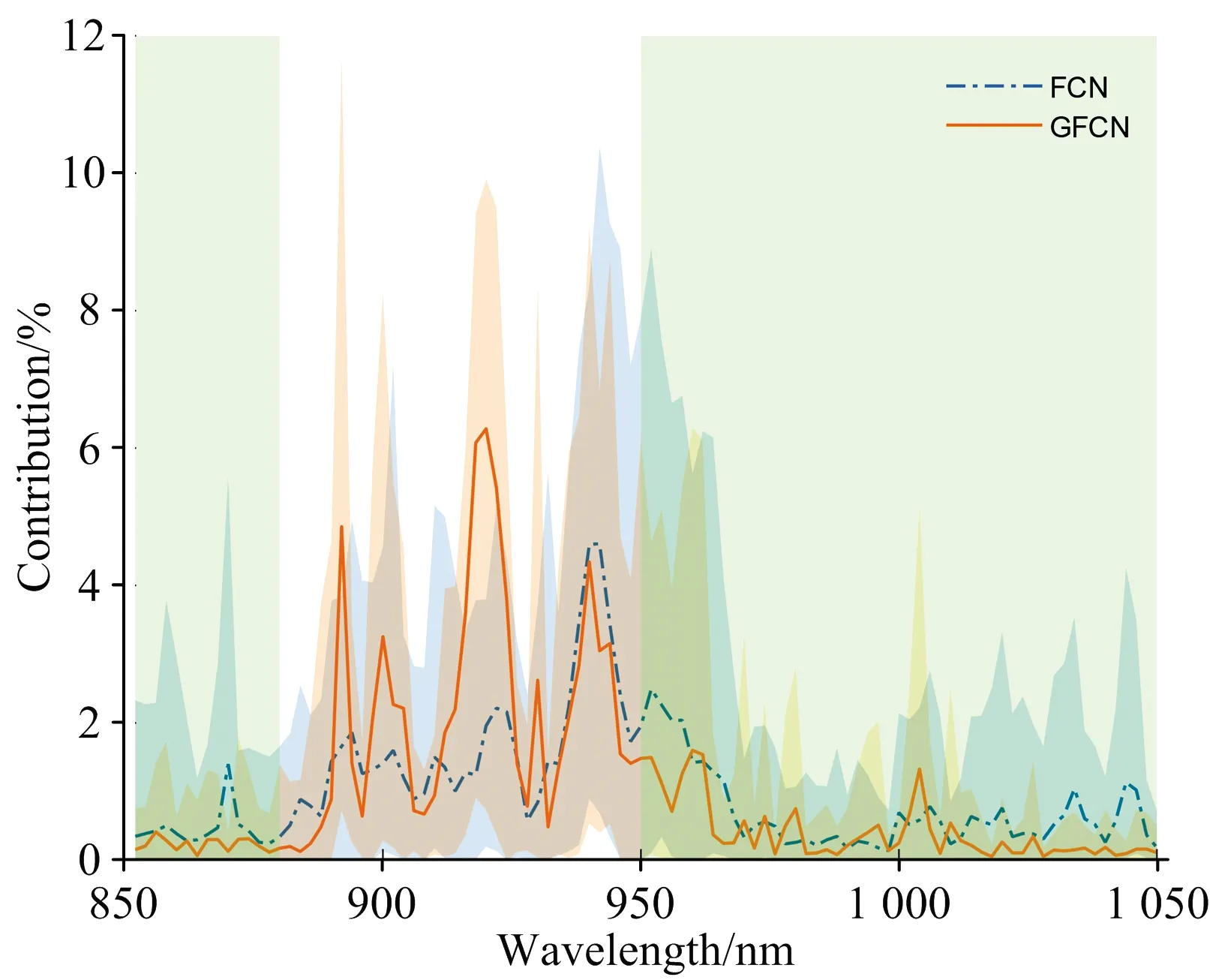
图7 预测fat成分的FCN和GFCN模型各波长的贡献占比

4 结 论

提出了一个基于分组全连接网络的定量分析模型GFCN。它在FCN模型的基础上，将原有的全连接层改为分组全连接层，不仅降低了模型的参数量，同时还提高了预测效果。对Tecator和IDRC2018数据集使用PLS，FCN和GFCN分别建立回归模型，GFCN的预测效果优于PLS和FCN。实验结果表明，GFCN是一种有效的定量分析方法。