基于改进鸽群算法的无线传感器网络定位方法*
崔焕庆,张 娜,罗汉江
(山东科技大学计算机科学与工程学院,山东 青岛 266590)
无线传感器网络(Wireless Sensor Networks,WSNs)由大量传感器节点组成,广泛应用于环境监测、智慧城市、灾害救援和目标追踪等领域。 确定传感器节点的位置信息为许多位置感知协议和应用程序提供了基础支持,因此,节点定位是无线传感器网络的关键技术之一[1]。 由于成本因素,为每个节点配备全球导航卫星系统(Global Navigation Satellite System,GNSS)进行定位是不现实的。 目前常用的方法是先给部分节点配备GNSS 以获取其自身位置并辅助其他节点进行定位,将已知自身位置的节点称为锚节点,其他节点称为未知节点[2]。
目前定位算法可分为无需测距和基于测距两类[3]。 前者根据节点间的连通信息估计距离,后者需要测量节点之间的距离或角度。 相比于无需测距的定位算法,基于测距的定位算法精度更高[4]。 获得距离后,使用三边测量、极大似然估计(Maximum Likelihood Estimation,MLE)等估计节点位置[5]。 相比于传统的定位算法,智能优化算法计算精确、计算复杂度低,被广泛应用于节点定位中。 ISSADVHop[6]算法通过修正DV-Hop 的平均跳距,并使用佳点集和Levy 飞行策略对麻雀搜索算法进行改进,改善了定位精度。 AWL-MC[7]算法采用非线性映射曲线距离分析对未知节点进行粗略的相对坐标定位,再通过线性变换将相对坐标转换成绝对坐标,最后采用自适应Levy 飞行优化鲸鱼算法,以提高定位精度。 OLSSO[8]算法先通过Bounding-box 方法得到未知节点可能存在的区域以初始化个体,后将加权中心反向学习策略与群居蜘蛛群优化算法相结合,具有较高的定位精度和较快的收敛速度。
目前,鸽群算法(Pigeon Inspired Optimization,PIO)[9]已广泛应用于各个领域,PIO 相比于粒子群优化(Particle Swarm Optimization,PSO)[10]、蝙蝠算法(Bat Algorithm,BA)[11]等,具有收敛速度快、参数较少和稳健性强等优点,但是容易陷入局部最优[12]。 为此,本文提出了一种基于改进鸽群优化(Modified Pigeon Inspired Optimization,MPIO)的定位算法。 本文的主要贡献有:①为了解决PIO 容易陷入局部最优的问题,设计了一种改进鸽群算法即MPIO 算法,在保持快速收敛能力的同时,提高了PIO 的计算精度。 ②将MPIO 算法应用于无线传感器网络节点定位以提高性能。
本文组织如下。 第一部分介绍了网络模型,第二部分介绍了标准鸽群算法,第三部分介绍了MPIO 算法及其在定位中的应用,第四部分给出了仿真实验和结果分析,最后第五部分总结了全文。
1 网络模型
假设WSN 由N个传感器节点组成,节点在部署完后不再移动。 锚节点数为M,第i个锚节点的坐标记为Ai=(xai,yai)。 第j个未知节点的实际坐标记为Uj=(xuj,yuj),估计坐标记为^Uj=(^xuj,^yuj)。传感器节点通信范围是一个半径为R的圆,锚节点向其通信范围内的节点广播信息,所广播的用于辅助未知节点定位的信息称为信标信息,包含锚节点坐标和发送信号强度两个字段。 传感器节点使用接收信号强度(Received Signal Strength,RSS)测距,RSS 采用对数-常态分布无线信号传播模型[13],即:
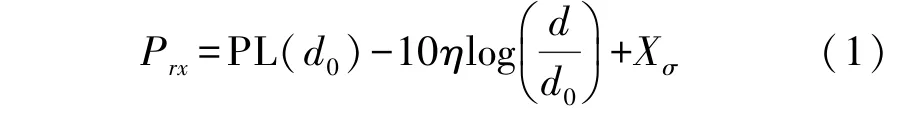
式中:d0为参考距离,PL(d0)为传播距离为d0时的接收信号功率。d为参考节点与未知节点间的距离,Prx为传播距离为d时的信号接收功率。η为路径损耗因子,Xσ为均值为0,标准差为σ的高斯变量。
在实际应用中,由于多径衰弱、信号传播不稳定和噪声等因素,传感器节点的通信范围不是一个规则的圆,所以使用通信不规则度(Degree of Irregularity,DOI)进行建模[14]。 DOI 值越高,通信范围受环境影响越严重。 DOI 定义如下:

式中:Kθ表示第θ个方向上的不规则度,满足|K0-K359|≤DOI,r∈[0,1]是一个服从均匀分布的随机数。 使用DOI 后的信号传播模型定义为:

设锚节点Ai和未知节点Uj的实际距离为dij,使用RSS 测得的距离为^dij。 通过最小化dij与^dij之差来达到估计未知节点位置的目的,所以使用智能优化算法定位的适应度函数定义如下:

式中:n为Uj通信范围内的锚节点数,X为智能优化算法中的个体位置。
平均定位误差(Average Localization Error,ALE)定义为全部未知节点估计坐标与实际坐标之间欧氏距离的均值,即:
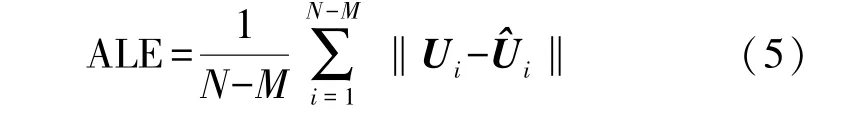
2 标准鸽群算法
PIO 是模仿鸽子归巢行为的一种智能优化算法。 鸽子归巢可分为两个阶段,在不同阶段使用不同的导航工具。 在地图和指南针算子阶段,鸽子通过感知磁场生成地图,把太阳作为指南针调整飞行方向。 在飞向目的地的过程中,其对磁场和太阳的依赖性减少。 在D维搜索空间中,第i只鸽子的位置Xi和速度Vi按照下式进行更新:
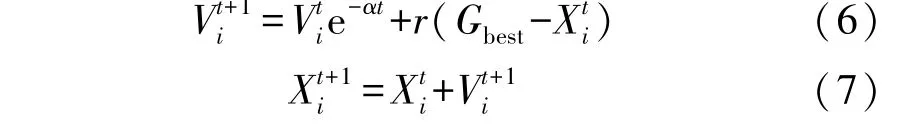
式中:t为当前迭代次数,α∈(0,1)为地图和指南针因子,Gbest为全局最优位置。 记T1max为该阶段最大迭代次数,当t>T1max时,进入下一阶段。
在地标算子阶段,每次迭代时先根据适应度值将鸽子排成非减序,保留前一半鸽子;然后在剩余鸽子中计算加权中心位置作为鸽子飞行的参考方向。鸽子位置更新如下:

式中:Np为鸽子总数,Xc为加权中心位置,f(·)为适应度函数。 记T2max为该阶段最大迭代次数,当t>T2max时,地标算子停止工作。
3 改进鸽群算法
3.1 地图和指南针算子阶段
在该阶段,PIO 算法的全局搜索能力主要由指数权值W=e-αt决定,使得鸽群在迭代过程中多样性呈递减趋势并逐步向最优解收敛[15]。 这种更新方式使算法快速收敛,但是全局搜索能力较差。 地图和指南针因子α在很大程度上决定了算法全局搜索能力的优劣。 图1 展示了指数权值W在T1max=50 时的变化情况。α=0.3,t<15 时,W<0.75,种群多样性快速减少;而t≥15 时,W≈0,种群多样性丧失,算法主要在Gbest附近进行局部搜索,失去了全局搜索能力,导致过早收敛。α=0.02,t=50 时,W=0.38,算法不易收敛。 0.02<α<0.3 时,W呈指数递减趋势,种群多样性快速减少,导致较差的全局搜索能力。
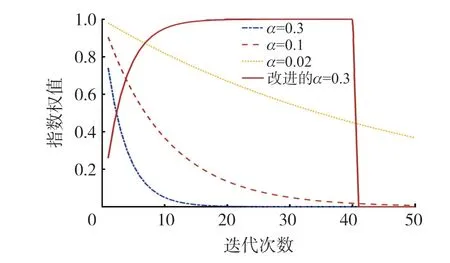
图1 指数权值随迭代次数变化图
为平衡全局搜索与局部搜索,改进式(6)为:
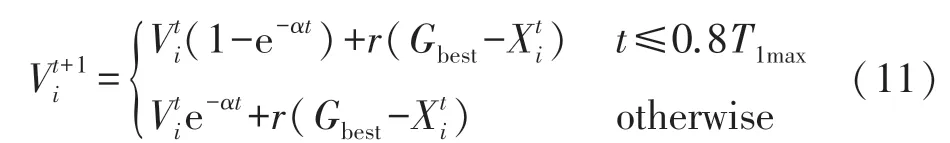
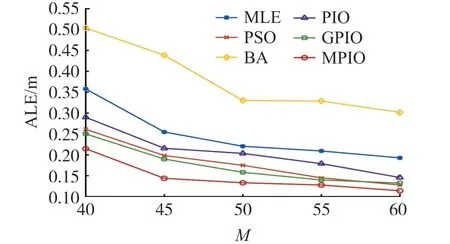
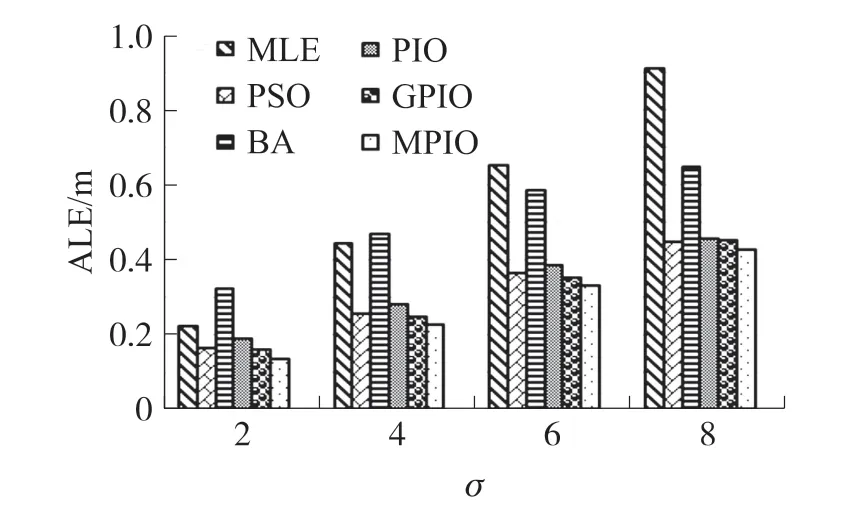
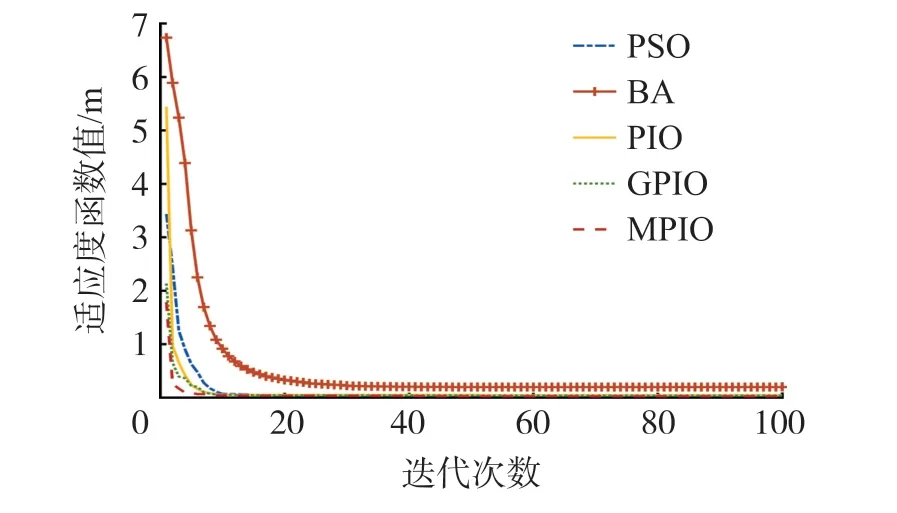
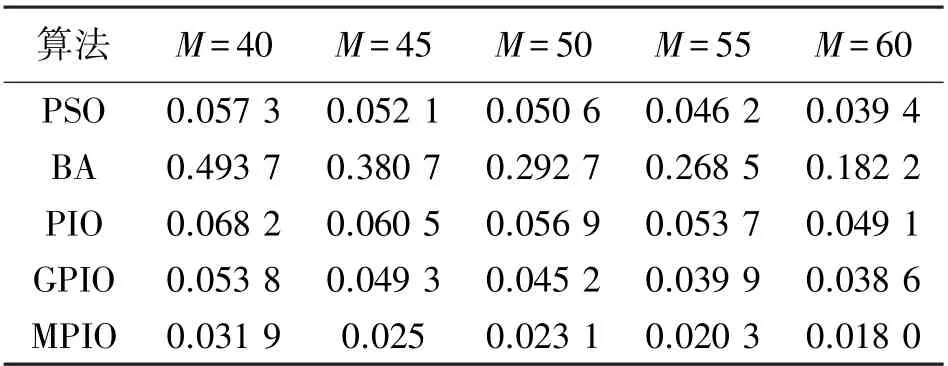
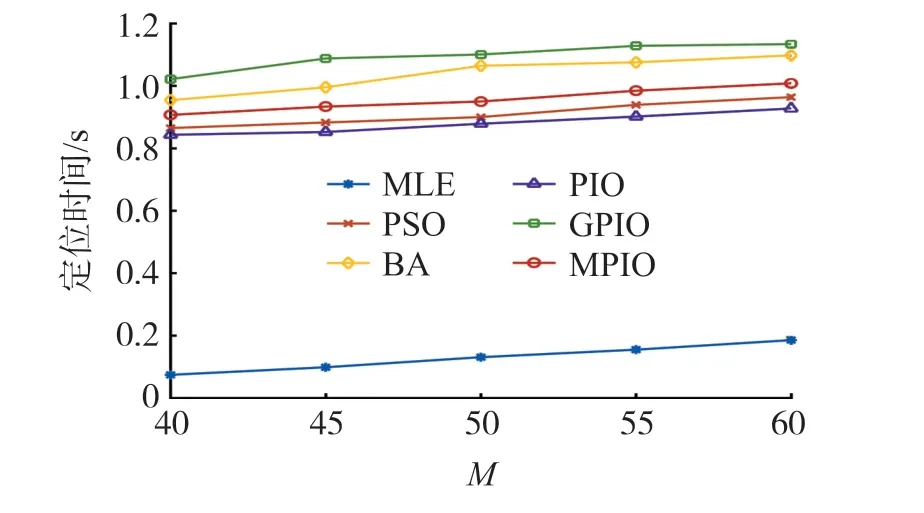
α=0.3 时,改进后的指数权值W′=1-e-αt的变化情况如图1 所示。t≤4 时,W′<0.6,仅在Gbest附近搜索,能够更快地在Gbest处收敛;4 在该阶段,MPIO 不删除鸽子,而是按照适应度值排序后将鸽子分为两组种群,在不同种群中用不同方式进行迭代更新。 定义: 前N′p只鸽子为一组,鸽子位置更新公式为: 式中:Xpi为第i只鸽子的局部最优位置。 剩余Np-只鸽子分一组,使用随机游走和捕食机制更新鸽子位置。 随机游走是在最优解附近产生局部新解,在一定程度上能够使算法跳出局部最优,即: 式中:β∈[-1,1]是一个随机变量,E∈(0,1)为一个常数,为第i只鸽子在第t次迭代时的脉冲发射率。 捕食机制中,鸽子会减少响度Li,增大ri,择优选择鸽子位置并更新Li和ri,即: 式中:ε∈[0,1]为常数,表示响度衰减系数;μ>0 为常数,表示脉冲增强系数;=0.7 表示第i只鸽子的初始脉冲发射率,设置每只鸽子的响度Li初始值为0.1。 使用MPIO 进行定位的基本思路是:锚节点广播信标信息后,未知节点使用RSS 测量与邻居锚节点的距离。 在测得至少3 个相邻锚节点的距离、位置后,便采用MPIO 算法进行位置计算。 具体流程如算法1 所示。 输入:未知节点U 及其相邻锚节点集合A输出:^U=(^xu,^yu)1. 初始化D,Np,T1max,T2max,α,E,ε,μ 2. 使用RSS 估算U 到每个锚节点的距离3. 随机生成Np 只鸽子,第i 只鸽子坐标为Xi(i =1,2,…,Np)4. 使用式(4)计算适应度函数值5. Gbest←最佳位置6. for t←1 to T1max do 7. 所有鸽子根据式(11)和(7)更新位置8. 使用式(4)计算适应度函数值9. 更新Xp 和Gbest 10. t←t+1 11. end for 12. for t←1 to T2max do 13. 根据适应度函数值对鸽子进行排序14. 根据式(12)和(13)更新N′p和Xc 15. 前N′p只鸽子根据式(14)更新位置16. 其余鸽子根据式(15)更新位置17. 使用式(4)计算适应度函数值18. 更新Xp 和Gbest 19. t←t+1 20. end for 21. return Gbest 算法1 第1 行初始化必要参数,第2 行使用RSS 测量未知节点与锚节点的距离,第3~5 行初始化鸽群,第6~11 行是地图和指南针算子阶段,第12~20 行是地标算子阶段,每阶段使用不同的公式更新鸽子位置。 第21 行返回Gbest作为未知节点U的估计位置。 该算法的主体是两个for 循环,每个for 循环都是根据上述公式对鸽子位置进行更新,其中第2 个循环需要对鸽子进行排序,因此其时间复杂度为O(NpT1max+NpT2maxlogNp)。 本文使用MATLAB R2016b 进行仿真,所有算法运行50 次并取均值作为实验结果。 在定位精度上将MPIO 与MLE、PSO、PIO、BA、GPIO[16]算法相比较。 各算法参数设置如表1 所示,其他实验参数设置如表2 所示。 表1 优化算法的参数设置 表2 其他实验参数设置 在锚节点数M=50,通信半径R=20,25,30,35,40 时的结果如图2 所示。 随着R的增加,平均定位误差ALE 随之下降,原因在于R的增大使得孤立节点的数量大幅减少,距离测量更加准确。 BA 算法的ALE 最大,因为其在较大的部署区域内寻优能力较差;其次是MLE,它计算简单,但是求解能力较差;其次是PIO 和PSO 算法,因为PSO 和PIO 都有容易陷入局部最优的局限性;GPIO 通过在距离较近的种群个体上添加高斯变异使种群个体随机发散,并没有有效解决算法陷入局部最优。 MPIO 算法的定位精度始终优于其他算法,GPIO、MPIO 相比于PIO 分别提高了30%、60%。 MPIO 算法具有更优的求解能力,一方面是因为添加了自适应调整机制,使种群个体快速寻找全局最优并提高了种群在最优解附近的局部搜索能力;另一方面是因为种群分组和随机游走机制增加了种群多样性,使算法能够跳出局部最优。 图2 通信半径对定位误差的影响 在通信半径R=30,锚节点数M=40,45,50,55,60 时的结果如图3 所示。 随着锚节点数量的增加,未知节点接收到的信标信息更多,平均定位误差ALE 会随之下降。 BA 算法的ALE 最大,因为其在较大的部署区域内寻优能力较差;其次是MLE,它计算简单但是求解能力较差;其次是PIO 和PSO,因为PSO 和PIO 都容易陷入局部最优;GPIO 没有有效改进PIO 容易陷入局部最优的缺陷。 MPIO 算法的定位精度始终优于其他算法,GPIO、MPIO 相比于PIO 分别提高了33%、60%。 MPIO 算法的自适应调整机制和随机游走机制增加了种群多样性,有效提高了PIO 算法的求解精度。 在相同条件下,MPIO算法所需的锚节点数量最少,能有效减少网络成本。 图3 锚节点数量对定位误差的影响 在锚节点数M=50,通信半径R=30,测距误差σ=2,4,6,8 时的结果如图4 所示。 随着σ的增加,平均定位误差ALE 也随之增大。 MLE 受测距误差影响最大;其次是BA 算法,因为其在较大的部署区域内寻优能力较差;其次是PIO 和PSO,因为PSO和PIO 都容易陷入局部最优;GPIO 没有有效改进PIO 容易陷入局部最优的缺陷。 MPIO 算法的定位精度始终优于其他算法,GPIO、MPIO 相比于PIO 分别提高了27%、49%。 MPIO 算法的自适应调整机制和随机游走机制使算法跳出局部最优,有效提高了PIO 算法的求解精度。 相同条件下,MPIO 算法受测距误差的影响最小。 图4 测距误差对定位误差的影响 在锚节点数M=50,通信半径R=30,通信不规则度DOI=0.05,0.1,0.15,0.2,0.25 时的结果如图5所示。 DOI 越大,节点通信范围越不规则,平均定位误差ALE 也随之增大。 BA 算法受DOI 影响使得ALE 最大,因为其在较大的部署区域内求解能力较差;其次是MLE,它计算简单但是求解能力较差;其次是PIO 和PSO,因为PSO 和PIO 都容易陷入局部最优;GPIO 没有有效改进PIO 容易陷入局部最优的缺陷。 MPIO 算法的定位精度始终优于其他算法,各算法受DOI 影响定位误差的波动幅度分别为:MLE 0.79%、PSO 1.12%、BA 4.63%、PIO 1.32%、GPIO 1.34%、MPIO 0.91%。 MPIO 算法的自适应调整机制和随机游走机制有效改进了PIO 算法容易陷入局部最优的缺陷。 相同条件下,MPIO 算法受DOI 的影响变化幅度较小。 图5 DOI 对定位误差的影响 在锚节点数M=50,通信半径R=30 时的收敛曲线如图6 所示。 在算法迭代前期MPIO 算法的收敛最快,其次是GPIO、PIO、PSO 和BA。 图6 不同算法收敛曲线 图7 和表3 分别显示了在锚节点数M=40,45,50,55,60 时不同定位算法的定位时间和最优适应度值。 可以看出随着锚节点数量的增加,定位时间也随之增加,各定位算法平均定位时间依次为MLE 0.129 s、PIO 0.881 s、PSO 0.92 s、MPIO 0.95 s、BA 1.04 s、GPIO 1.09 s。 随着锚节点数量的增加各优化算法的适应度值减小,各优化算法的平均适应度值依次为MPIO 0.023、GPIO 0.045、PSO 0.049、PIO 0.057、BA 0.323。 由于MLE 算法计算简单所以定位时间最短,但是由4.1 节分析可知MLE 算法定位精度较低;BA 具有较长的定位时间和较高的最优适应度值;由于PIO 收敛速度较快所以定位时间较短,但是由于容易陷入局部最优导致PIO 的最优适应度值高于MPIO;由于GPIO 频繁使用高斯变异增加种群多样性提高算法求解精度,使最优适应度值较低,但是定位时间最长;由于MPIO 在PIO 的基础上进行改进来使PIO 跳出局部最优,所以定位时间较PIO 长,但是具有最低的适应度值,算法求解精度最高。 表3 各优化算法的最优适应度值 图7 锚节点数量对定位时间的影响 本文针对PIO 算法容易陷入局部最优的缺陷,提出了一种基于改进鸽群算法(MPIO)的无线传感网络定位算法。 MPIO 的第一阶段通过自适应调整机制来平衡全局搜索与局部搜索能力,并同时保证较快收敛速度;第二阶段保留全部鸽子并分组,使用随机游走等机制增加种群多样性,提高了算法的求解精度。 定位过程中首先使用RSS 进行测距,然后使用MPIO 进行定位。 仿真结果表明,MPIO 算法相比于传统的定位算法和其他的优化算法,具有较高的定位精度和较快的收敛速度。3.2 地标算子阶段
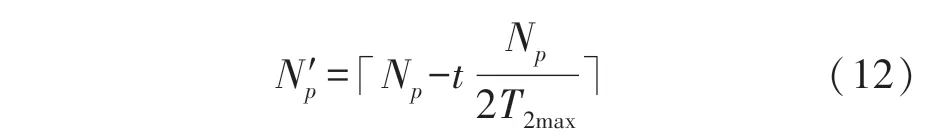
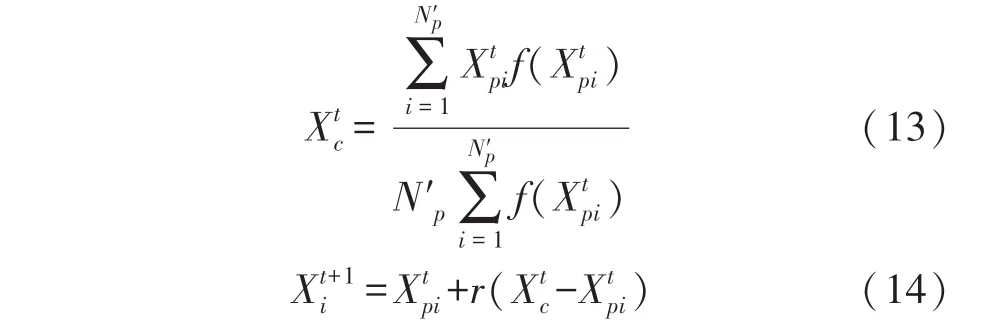
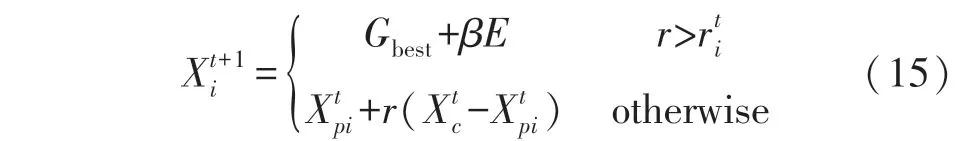
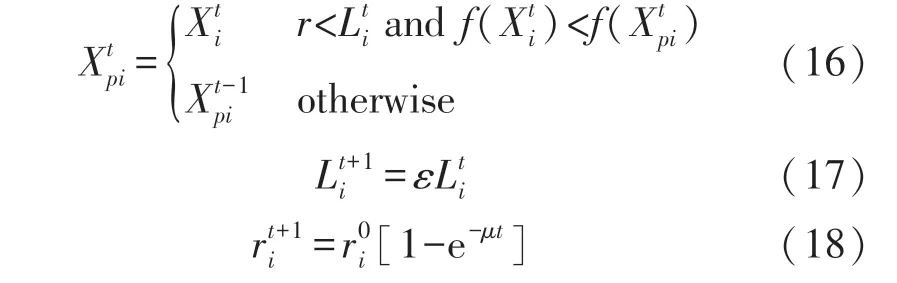
3.3 基于MPIO 的定位算法


4 仿真实验


4.1 定位精度对比


4.2 收敛速度对比
5 总结

