基于MPS方法模拟低雷诺数方柱绕流问题

兰小杰，赵伟文，万德成，邹 丽

(1.上海交通大学 船海计算水动力学研究中心(CMHL) 船舶海洋与建筑工程学院，上海 200240;2.大连理工大学 船舶工程学院，辽宁 大连 116024)

柱体绕流问题是流体力学领域的经典问题和研究热点之一。当流体流过柱体时，会发生分离流、涡流等很多复杂的流动现象，准确地模拟这些现象一直是计算流体力学的目标之一。同时柱体绕流也是现代工程中经常遇到的问题，风吹过高层建筑物，水流流过桥墩，海流流过海洋平台等都是典型的柱体绕流。当流体流过这些结构物时，结构物会受到很大的作用力，对结构的强度提出了更高的要求。

柱体绕流经常被作为标准验证算例，对其的研究已经进行得相当广泛。Perry等[1]、Davis等[2]、Okajima等[3]许多学者用试验的方式对方柱绕流的流场及方柱受力进行测量，还有大量学者用基于网格的计算流体力学方法对方柱或圆柱绕流进行了相关研究[4-8]。但是利用无网格粒子法对柱体绕流进行模拟的研究还不算很多。Yildiz等[9]提出了一种用于光滑粒子流体动力学(smoothed particle hydrodynamics method，简称SPH)方法的改进固体边界处理方法，多边界切线法(multiple boundary tangent method，简称MBT)解决了粒子法不能正确处理复杂流域中弯曲边界的问题，第一次用SPH方法模拟了雷诺数为50的圆柱绕流。Shadloo等[10]用不可压缩光滑粒子法(ISPH)模拟雷诺数为300的方柱绕流，说明了ISPH方法能够自然地捕获钝体绕流的流分离、涡旋脱落等复杂的物理现象。Marrone等[11]使用弱可压缩的SPH方法模拟了低雷诺数时钝体周围黏性流的演变。Koshizuka等[12]用MPS方法对雷诺数为100和200的柱体绕流进行了模拟，成功地模拟出了存在于圆柱体和方柱体后面的卡门涡街。国内孙鹏楠[13]对传统光滑粒子法进行改进，并用改进后的方法对圆柱绕流进行模拟，对模拟得到的流场进行细致的分析并与试验结果进行对比，证明光滑粒子法模拟圆柱绕流是有效的。但相较于圆柱，方柱由于尖锐直角的存在，对其进行模拟更具挑战性。

MPS方法是在SPH方法的基础上发展起来的，最先由Koshizuka和Oka[14]于1996年提出，主要用于求解不可压缩流动问题。MPS 继承了SPH 的无网格思想，用拉格朗日粒子携带空间流场的信息，粒子具有质量、动量、能量等物理量，粒子间的影响通过核函数来实现。近年来，MPS方法得到了长足的发展，除了在液舱晃荡[15]等粒子法传统优势领域的应用外，研究人员还把MPS方法的应用扩展到了多相流动[16-17]、声学[18]等领域。采用基于MPS方法自主开发的无网格法求解器MLParticle-SJTU，对雷诺数分别为40、200及1 000的方柱绕流进行仿真模拟分析，得到3种雷诺数下方柱绕流流场及方柱受力，并与文献中的结果进行对比验证。

1 数值方法

1.1 控制方程

MPS方法的控制方程包括连续性方程和N-S方程，对于不可压缩流体，分别可以写成式(1)、式(2)形式：

(1)

(2)

式中：P、V分别为压力和速度，ν、ρ分别表示流体的运动黏性系数和密度，f表示质量力。MPS方法的控制方程为拉格朗日形式，因此不存在对流项。

1.2 核函数

与SPH方法不同，MPS中核函数只是起着权函数的作用，求解过程不需要使用核函数的导函数，所以MPS方法的核函数只要求连续不要求光滑。采用的核函数选用Zhang等[19]推荐的核函数：

(3)

其中，l=|ri-rj|，表示粒子间距，le表示粒子的影响半径，一般根据需要选取合适的值即可。

1.3 不可压缩条件

采用被Lee等[20]改写过的混合源项法，表达式为：

(4)

(5)

其中，r是粒子的坐标，i、j为粒子的编号。

1.4 梯度模型

采用的梯度模型表达式为：

(6)

1.5 散度模型

在MPS方法的连续性方程中存在散度项，需要用核函数对其进行离散。采用的散度模型表达式为：

(7)

1.6 Laplacian模型

在文中MPS方法里使用的是Koshizuka[14]所给出的Laplacian模型，模型表达式为：

(8)

其中，λ是修正系数，引入λ是为了修正数值结果，使其与扩散方程的解析结果相一致，其表达式为：

(9)

2 数值模拟

2.1 计算模型

研究中，计算域示意如图1所示。设定方柱边长D为0.1 m，计算域大小设置为25D×12D。为消除入口边界对柱体绕流模拟的影响，计算域流体入口距柱体中心7D，计算域出口与柱体中心的距离为18D，从而确保尾流得到充分发展。为减少壁面边界对柱体周围流场的影响，两侧壁面距柱体中心的距离均设置为6D。计算坐标系原点在计算域左下角，x轴正方向为来流速度方向。粒子间距设置为Δx/D=25，计算雷诺数分别为Re=40、200及1 000。

图1 计算域示意Fig.1 Computational domain of flow around square

2.2 边界条件

2.2.1 入口边界条件

图2为流入流出边界的示意。图2(a)为初始状态，流入边界上的壁面粒子以指定的流入速度向右移动，流体颗粒被左侧壁面推动，也会以指定的速度向右流动，如图2(b)。当壁面向右移动距离达到指定值时，壁面退回初始位置，原推板位置填入虚粒子(图2(c))，赋予原推板位置处的虚粒子速度和压力等物理量，将虚粒子转变成为流体粒子，计算继续进行(图2(d))。推板不断往复运动，推动流场中所有流体粒子以指定速度向右流动，完成流动的模拟。

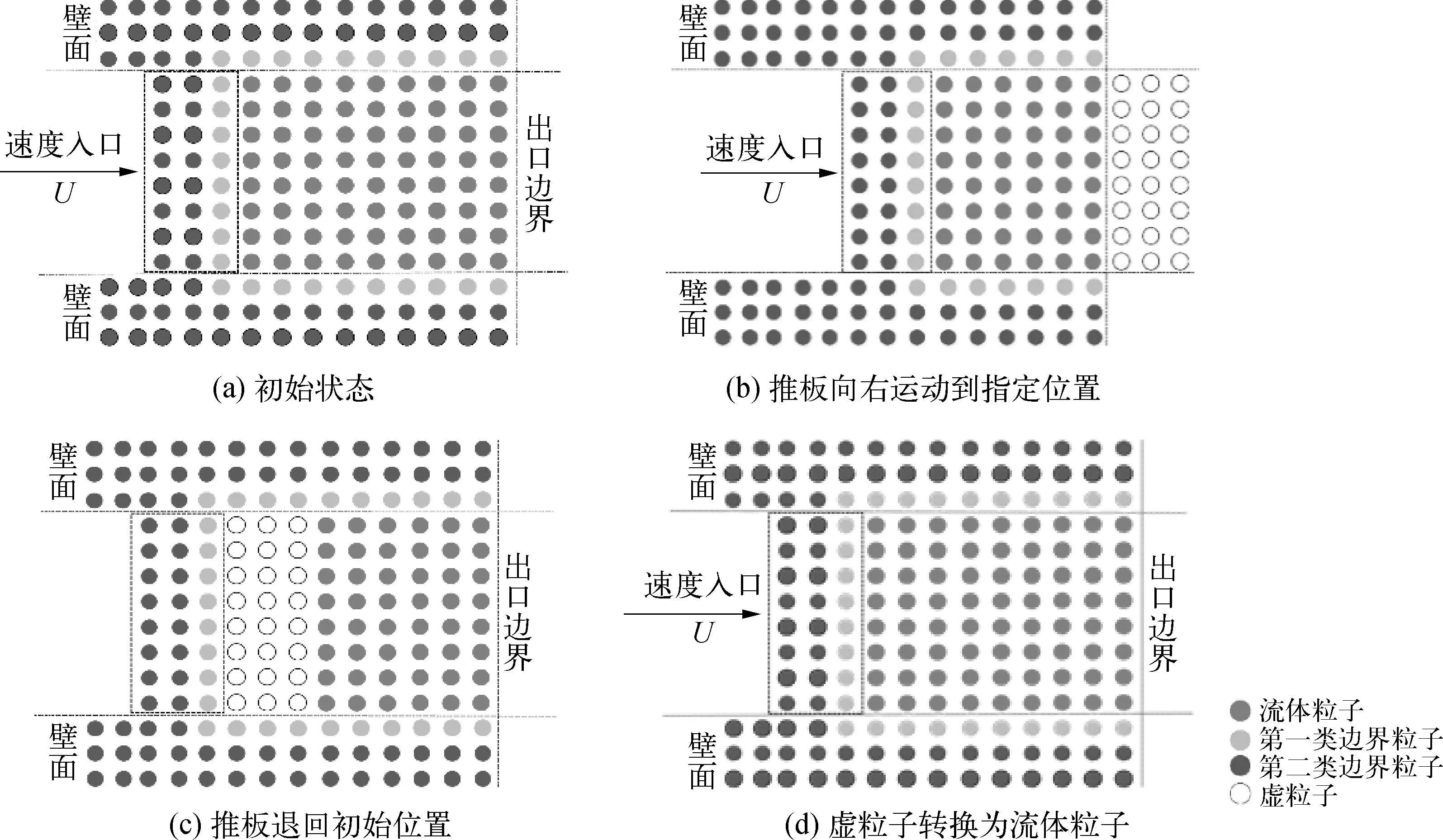
图2 流入流出边界示意Fig.2 Diagrammatic drawing of inlet and outlet

2.2.2 出口边界条件

如图2所示，当流体粒子流出计算域时，把流体粒子转换成虚粒子，不影响其它流体粒子。虚粒子的质量、密度等物理量都是0，等待替补到入口边界。虚粒子填入由于推板后退产生的空隙中后，会被赋予相应的物理性质，变成新的流体粒子，重新进入计算域。

2.2.3 壁面边界条件

在MPS方法中，壁面边界由多层粒子组成，如图2中所示。内层与流体颗粒相邻的边界粒子称为第一类边界粒子，第一类边界粒子参与压力Poisson 方程的求解。外层由第二类边界粒子组成，第二类边界粒子的压力通过周围的流体粒子和第一类边界粒子外插出来。柱体壁面边界粒子除了速度始终设为0以外，其它属性如作用域半径、密度和质量等与流体粒子完全相同，柱体壁面为无滑移壁面。上下边界壁面给滑移壁面条件，可以更好地模拟均匀来流。

2.3 来流条件

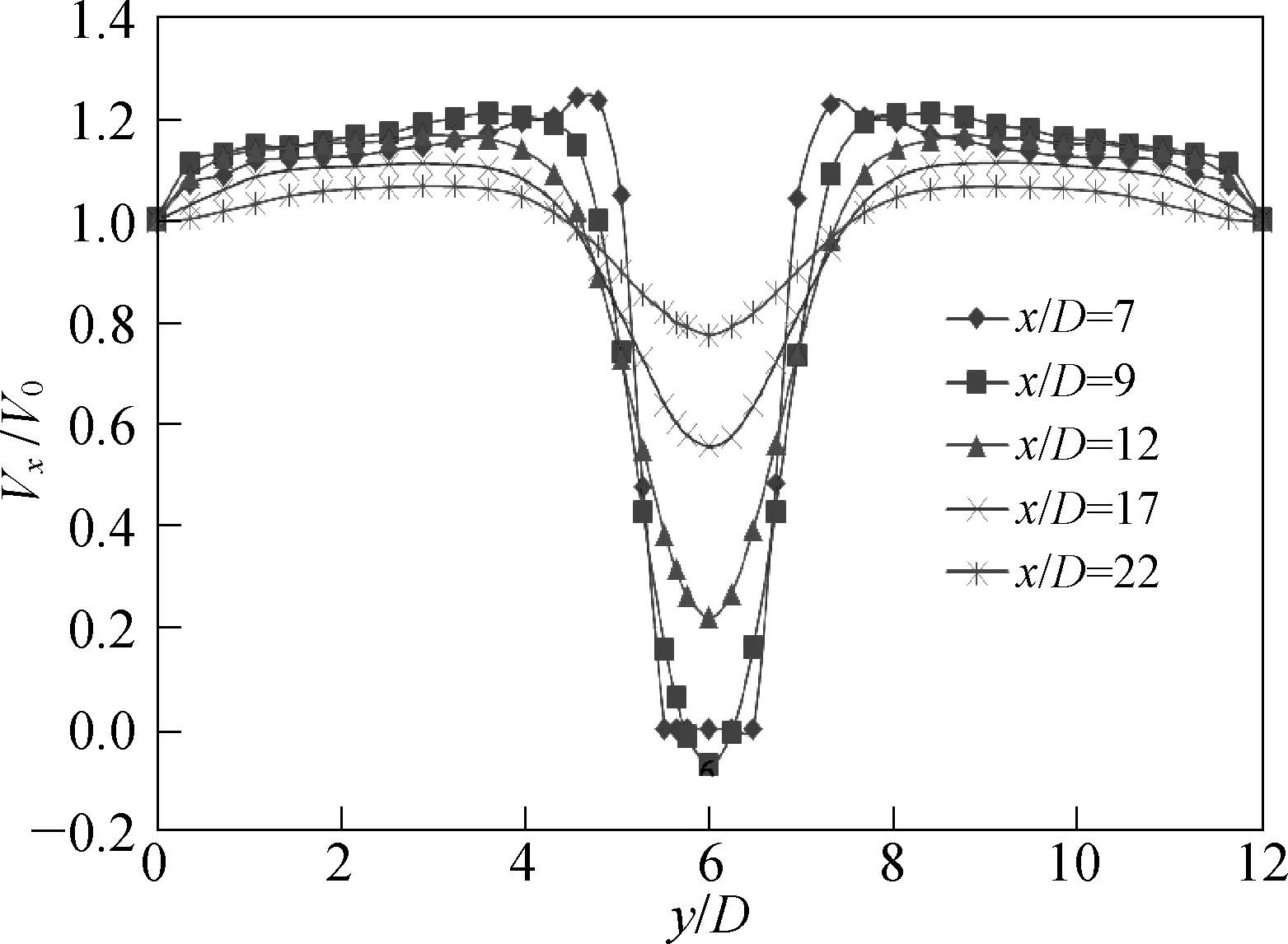
文中来流条件设定为均匀来流，通过模拟管道内均匀流对均匀来流条件进行验证。选取柱体绕流雷诺数Re=40的工况，设定来流速度为0.000 4 m/s，模拟没有柱体时的管道流动。图3为模拟得到的整体速度云图，管道整体速度都在0.000 4 m/s附近。图4为流动充分发展后x/D=7、9、12、17、22处的x方向时均速度，其中x/D=7处是放置方柱的位置。从图4中可以看见，不同位置下的x方向速度剖面都呈直线且在0.000 4 m/s 处，误差小于0.1%，精确模拟均匀管道流。

图4 不同流向位置处x方向速度Fig.4 The velocity in tne x direction at different positions

3 结果分析

3.1 水动力系数

在方柱绕流问题中，方柱主要受到的水动力包括阻力和升力。一般为了方便对比研究，需要对方柱受力进行无量纲化处理，得到时均阻力系数Cd、升力系数Cl和斯特劳哈尔数St，分别为：

(10)

式中：Fd和Fl分别为圆柱受到的阻力和升力；ρ为流体密度；U为流速；fs为斯特劳哈尔涡泄频率。表1为文中模拟计算得到的方柱绕流水动力系数结果。

表1 阻力系数和斯特劳哈尔数Tab.1 Drag coefficient and Strouhal number

以Sen等[21]的数值计算结果为参考，比较雷诺数Re=40时方柱的阻力系数Cd。文中计算得到Re=40时方柱的阻力系数为1.724，略大于Sen等[21]的计算结果1.67，误差为3.23%。平均升力系数为-0.009 2，接近于0，与试验结果及理论结果相符合。图5和图6分别是Re=40时升力系数时历曲线和升力功率谱密度，此时的升力系数曲线没有呈现出周期性，其中升力功率谱密度纵坐标|P1(f)|表示升力在各频率下的功率分量大小。

图5 Re=40，阻力系数和升力系数时历曲线Fig.5 Time history of the drag and lift at Re=40

图6 Re=40，升力功率谱密度Fig.6 Power spectral density of lift at Re=40

在Re=200的工况下，Gera等[22]计算得到的阻力系数为1.487，文中模拟计算得到的阻力系数平均值为1.496，误差为0.605%。图7为Re=200 时计算得到的阻力系数和升力系数时历曲线。在流动充分发展之后，图中升力系数曲线有明显的周期性，升力变化频率即为泄涡频率。图8为升力功率谱密度，最高的尖峰对应的横坐标为斯特劳哈尔数St=0.14，与Okajima[3]试验结果0.145相比，误差为3.57%。

图7 Re=200，阻力系数和升力系数时历曲线Fig.7 Time history of the drag and lift at Re=200

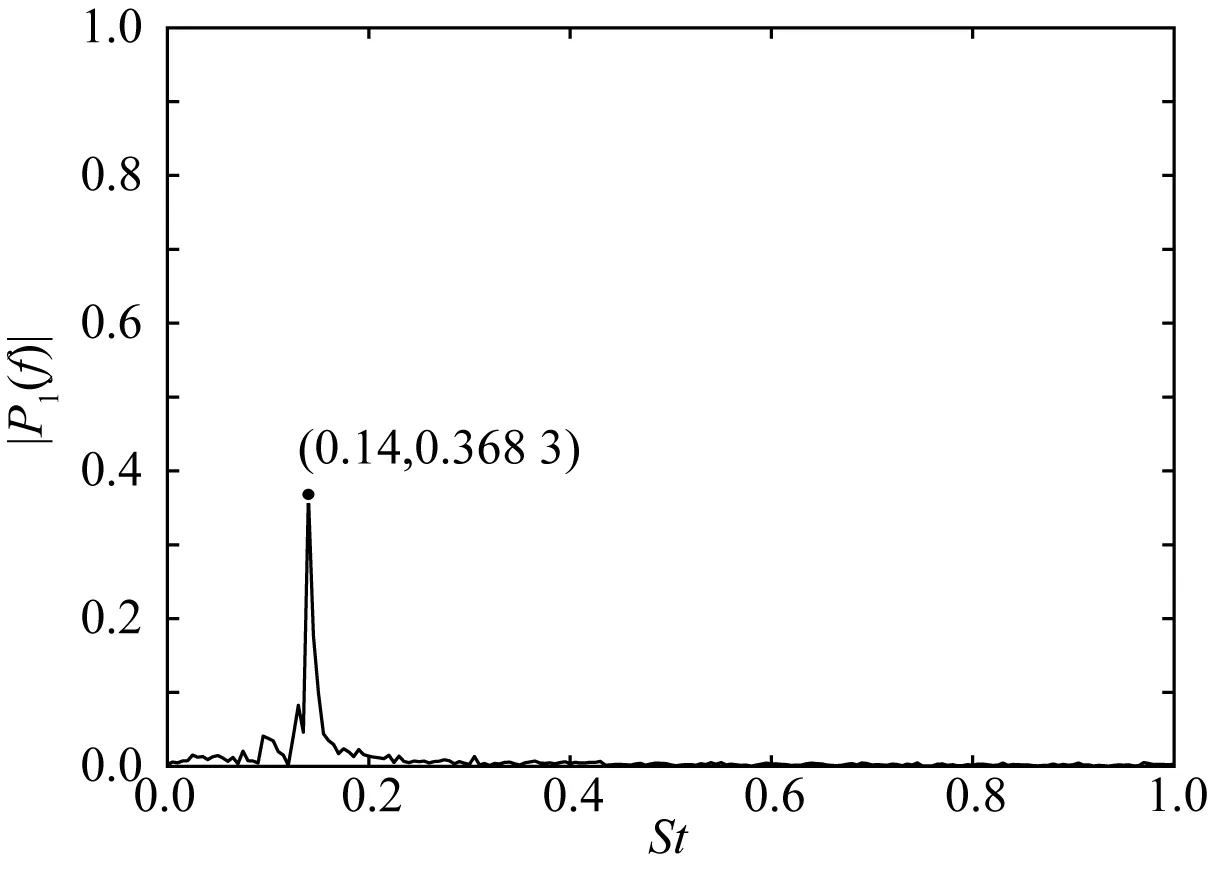
图8 Re=200，升力功率谱密度Fig.8 Power spectral density of lift at Re=200

Re=1 000时，阻力系数和升力系数时历曲线如图9、图10所示，计算得到的阻力系数为2.396，比王建春[23]用FVM方法计算的结果大7.44%，斯特劳哈尔数St为0.124，与王建春[23]的计算结果及前人试验结果相近。

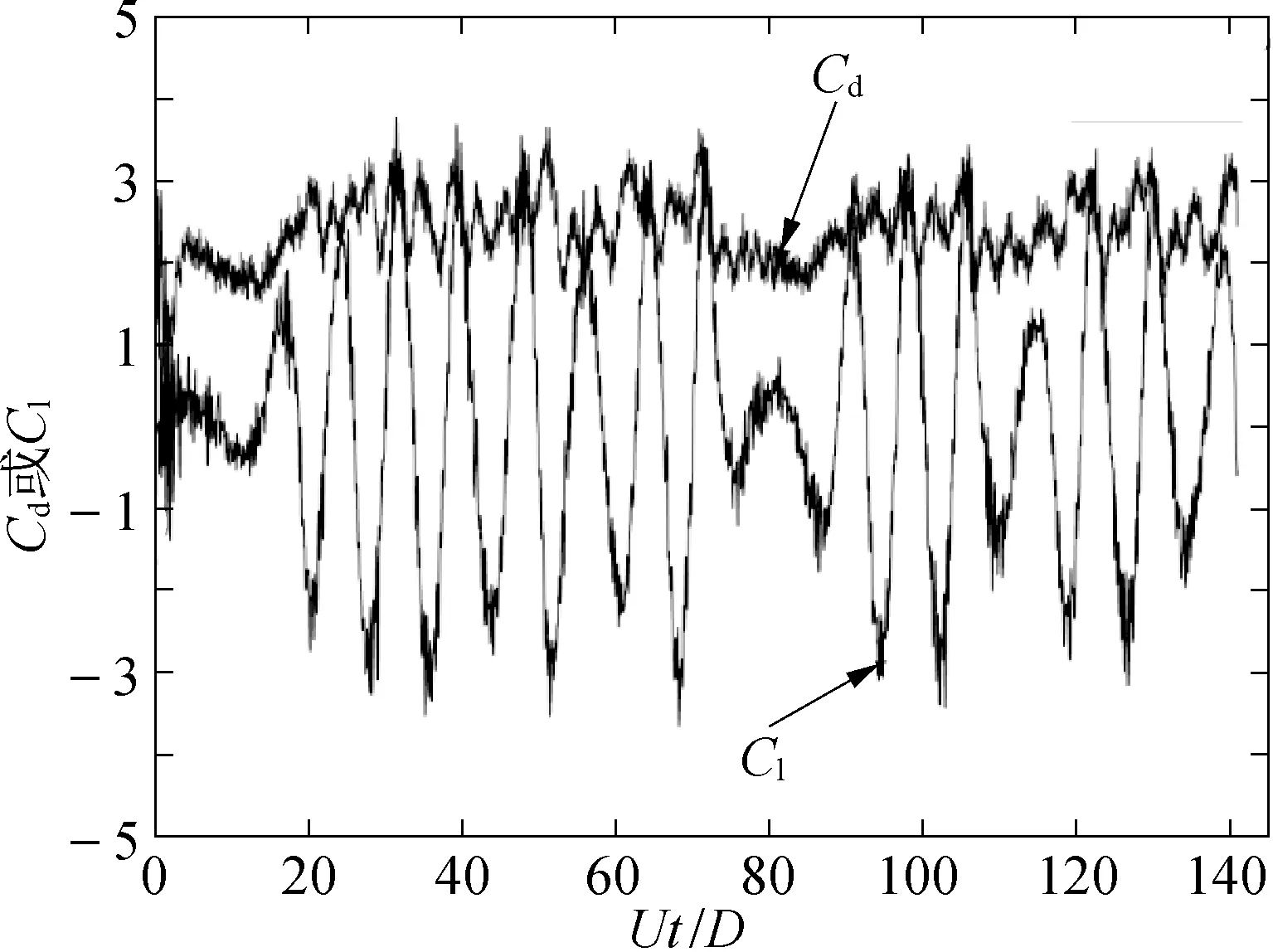
图9 Re=1 000，阻力系数和升力系数时历曲线Fig.9 Time history of the drag and lift at Re=1 000

图10 Re=1 000，升力功率谱密度Fig.10 Power spectral density of lift at Re=1 000

3.2 尾流流态分析

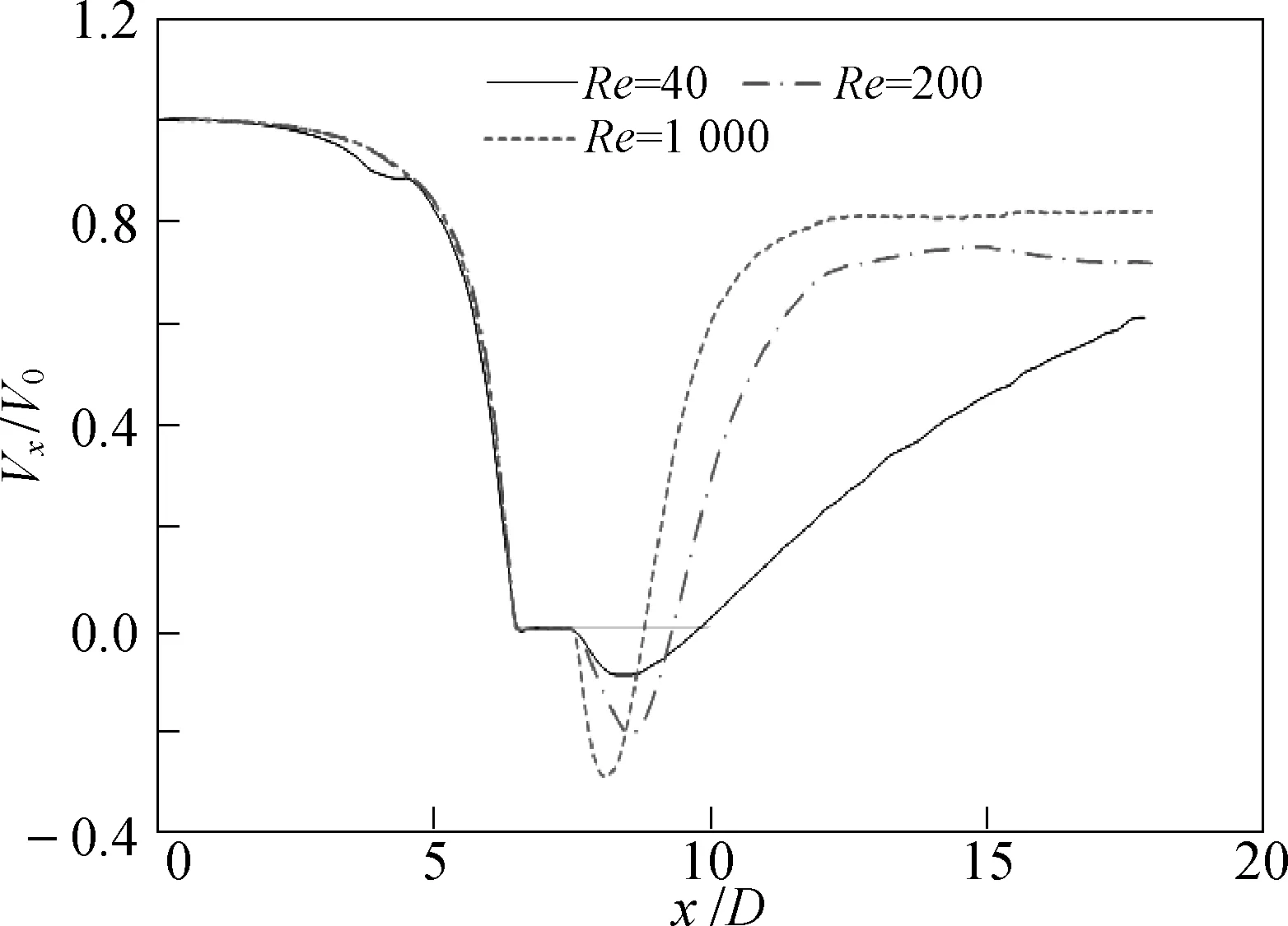
Re=40时，流场充分发展后，流动会趋于稳定，方柱后面出现一对上下对称的尾涡，不会发生涡脱落等现象，与前人试验及计算结果一致，图11为流场稳定后方柱周围流场示意。从图11可以看到，方柱周围流场是对称的，方柱前后速度较低，两侧速度较大。图12为模拟计算得到流场稳定后流线图，可以明显观察到方柱后方由于回流形成的对称尾涡，与Sen等[21]在文献中给出的结果相似。图13为y/D=6处即方柱中心线上x方向时均速度，图中速度小于0区域即为回流区，Re=40时回流区长度L与方柱边长D的比值L/D=2.38，根据Sen等[21]给出的经验公式L/D=-0.078 3+0.072 4×Re(5

图11 Re=40方柱周围流场Fig.11 Flow field around the square at Re=40

图12 Re=40方柱周围流线对比Fig.12 Stream-line around the square at Re=40

图13 不同雷诺数下y/D=6处x方向时均速度Fig.13 Time-mean velocity in x direction of y/D=6

图14 Re=40时，不同流向位置处x方向时均速度Fig.14 Velocity in x direction at different positions at Re=40

Re=200工况下，流场充分发展后，方柱后会出现旋涡周期性生成、脱落和卡门涡街现象。图15为两个不同时刻方柱周围速度场。从图15中可以看到，随着来流速度的增加，方柱周围流场越来越复杂，在雷诺数200时，方柱周围速度场不再呈现对称的性质，而是尾迹不停摆动。

图15 Re=200，方柱周围流场Fig.15 The flow field around the square at Re=200

图16展示了Re=200时一个周期里不同时刻方柱周围的流线，图17为不同时刻的涡量云图。从图16可以明显看到一个周期内，方柱尾涡的生成和脱落，一个周期开始时，方柱左下角的涡即将脱落；T/5时右上角的涡不断发展壮大，同时左下角重新生成小涡；之后左下角的小涡发展壮大，右上角的大涡开始迁移脱落，到2T/5时，右上角的涡完全脱落；然后左下角的涡迁移脱落，右上角生成小涡，再发展壮大，T时刻的流线与开始时刻几乎相同，方柱尾流中的旋涡完成一个周期的运动。此后尾涡将重复上面过程，不断生成小涡，发展，迁移，脱落，在下游形成著名的卡门涡街现象，从图17涡量云图中可以清晰地看到卡门涡街现象。

图16 Re=200，一个周期内方柱周围流线Fig.16 Stream-line around the square in a period at Re=200

图17 Re=200，整体涡量云图Fig.17 Voticity contours at Re=200

在MPS方法中，粒子按拉格朗日描述法进行自由运动，可以跟踪粒子每个时间步的位置，得到粒子的运动轨迹，即迹线图。图18为Re=200时，某两个粒子的迹线，从迹线中可以明显看到由于绕流的发生，当粒子运动到方柱后方时，发生了回流的现象。

当Re=1 000时，与Re=200时观察到的方柱绕流现象相似，方柱后方仍存在涡交替脱落现象。图19为方柱周围平均压强系数CP与文献[24]结果对比，A-B与B-C两个区域的平均压强系数与前人模拟结果吻合较好，C-D区域结果比文献结果略大。图20为方柱周围涡量图与王建春[23]的模拟结果对比，对比结果较好。还可以看到，由于流速增加，对流影响加强，涡的稳定性受到影响，两个涡脱周期内的涡脱落形式有一定的差别。图13中可以看到雷诺数为1 000时的回流区长度小于雷诺数为200时的长度，可能也是因为涡稳定性降低，脱落需要的发展长度变短。

图19 Re=1 000，方柱周围平均压强系数Fig.19 Mean-pressure coeffient over the cylinder at Re=1 000

图20 Re=1 000时方柱周围涡量云图Fig.20 Voticity contours around the square at Re=1 000

4 结 语

运用MPS方法，建立入口、出口边界条件，精确模拟出均匀流。在此基础上，成功模拟了雷诺数分别为40、200、1 000的二维方柱绕流。计算结果表明：

1) 在雷诺数为40时，方柱后方的尾涡不会脱落，随着雷诺数增加，方柱绕流流场流动状态由定常涡转变为周期性旋涡脱落状态，雷诺数为200和1 000时，尾涡都会脱落，出现明显的卡门涡街，且雷诺数为1 000 时涡的稳定性比雷诺数为200时低，回流区长度比雷诺数为200时短。

2) 用MPS方法计算得到的方柱升阻力系数、斯特劳哈尔数等特性与前人试验结果及计算结果接近，流场特征与前人结果相符，验证了MPS方法模拟低雷诺数下方柱绕流问题的可靠性及有效性。

但从图17和图20涡量云图中可以看到，模拟结果存在一定的数值噪声，造成这种噪声的原因之一可能是粒子分布不完全均匀。而且如果雷诺数继续增大，流速增加会加剧这种分布不均，进而造成模拟结果偏差较大。引入粒子位移修正技术(particle shifting technique)可能可以解决这个问题，减小模拟误差的同时增大可模拟的雷诺数。