水平井油水两相流电容阵列持率仪算法研究

李沁泽,刘军锋,高峰,戴月祥,彭威水,崔帅飞

(1.油气资源与勘探技术教育部重点实验室(长江大学),湖北武汉430100;2.长江大学地球物理与石油资源学院,湖北武汉430100;3.中国石油集团测井有限公司新疆分公司,新疆克拉玛依834000)

0 引 言

水平井油水两相随着油相和水相的流量和含水率的变化,水平井油和水的分布非常复杂。准确测量持水率参数是油水两相流产出剖面解释中非常关键的一步。传统的单探针持率仪居中测量在水平井油水两相流中并不适用。因此,目前普遍采用阵列探针的形式,在井筒截面中进行多点测量。为了满足漂流模型等流量解释模型的需求,需要准确获取平均持水率参数。目前针对水平井阵列探针的平均持水率测量方法已经有人做了大量的研究[1-7],如面积权重法、平均插值法和分层界面法等3种方法[6]。

在利用探针计算的局部持水响应来计算井筒中的平均持水率时,3种方法各有不同。面积权重法根据探针个数和位置,对井筒进行相应的面积划分,并作为探针响应值的权重系数。然后对所有区域局部水相面积统计求和,再除以井筒横截面总面积,从而计算出平均持水率。这种方法是客观的,考虑到了探针的分布,在分层流中具有一定的准确性。

平均插值法求取井筒中平均持水率时,对所有探针计算的局部持水率进行简单的加权平均。这种方法没有考虑到不同流型和不同含水率条件下持水率与探针响应个数的非线性关系,计算误差较大,也是一种依赖探针响应值的方法。

分层界面法是通过判断探针在油相还是在水相,或者油水边界处,来估算油水界面高度。通过计算在该高度范围内水相所占据的截面面积与井筒横截面总面积的比值,获得平均持水率。它可以在一定程度上准确计算出分层流中的平均持水率,但没有明确给出在油水边界处探针响应值归一化为油或者归一化为水的客观依据,通常是采用经验数值进行判断。

自然间断点法是在油水两相中根据探针响应值及油水标定值进行客观判别的方法,这种方法纯粹依据测量数据的自身分布特性。该方法可以用于油水两相流,计算平均持水率时对油水边界的判断。将自然间断法计算的平均持水率与关井持水率做了一致性比较,认为该方法可以有效地进行油水两相边界的划分以及平均持水率参数的计算。

1 实验与数据

利用多相流模拟实验平台,设计了油水两相在完全水平(90°)情况下不同流量以及不同含水率的实验方案。实验中油为柴油,水为自来水。模拟井筒内径为125 mm。流量范围为25、30、35、40、45、50、55、60、65、70、80、90、100、110、120、150 m3/d。实验方案中流量及含水率配比见表1。

表1 流量和含水率配比

实验中持率测量,采用CAT电容阵列持率仪(见图1)。该仪器有12个等间隔分布的电容探针,根据流体的介电常数进行测量[8-9]。实验中,主要测量编码上传的12个探头原始计数和CAT旋转角度。

图1 CAT电容阵列持率仪

根据杨梅和Trallero等的研究[10-12],通过实验照片和现场观察,在实验流量范围内流体流型为分层流(见图2)。

图2 流型分析图

2 实验数据分析

2.1 CAT数据预处理

由于制作工艺等原因,不同电容探针的响应特性存在差异。因此,将12个电容探针分别在纯水和纯油中进行标定测量,从而获得各个探针的响应范围(见表2)。

假定探针的响应与周围流体持水率是线性相关,结合探针的刻度值,

可通过式(1)换算出探针覆盖区域的局部持水率。

(1)

式中,Ywi为第i个探针的局部持水率;Coi为第i个探针的纯油响应,cps;Cwi为第i个探针的纯水响应,cps;Ci为第i个探针的原始响应,cps。

表2 CAT探针刻度值

2.2 自然间断点法原理及算法实现

自然间断点法是一种数据分类方法[13]。该方法认为数据内部存在天然的“断点”。通过找到这些“断点”可以对不同类别的数据进行分类处理。这种不同类别可以是某种被量化的属性,因此,这里将探针响应值作为分类属性。

基于有限个电容探针进行持水率插值成像时,所产生的插值数据集是围绕有限个峰值分布的。尽管不同探针在对相同流体测量时存在各种微小的差异,但是当进行归一化处理时,这种差异不明显。因此,当探针在纯水和纯油中测量时,插值数据集差异较小,峰值不明显。当探针在油水2相中进行测量时,插值数据会围绕2个峰值分布,分别是纯水中的极低值和纯油中的极大值(见图3)。

图3 25 m3/d和150 m3/d分别在10%、50%、90%含水率时的CAT响应插值分布注:SD_rcap为电容探针归一化后的响应值。x,y分别为井筒横截面坐标

显然,在油水两相中存在明显的2类数据,即油中的高值,水中的低值。在实际应用中,对电容阵列持率仪进行油水持水率分布的可视化表达时,需要对水相和油相进行不同颜色的渲染,此时油水边界响应值是获取颜色渲染边界的关键参数。同时,计算持水率时,需求取水相面积,同样需要确定油水边界响应值,划分数据边界就成为一个急待解决的问题。下面介绍利用自然间断点法找出2类数据边界的总体思路,及一种基于Java编程语言的具体实现算法。

2.2.1 采用自然间断点法求取平均持水率

自然间断点算法的核心思想是让数据类间差异最大化,类内差异最小化。基于这个思想,首先需要给出数据集的划分类别总数k。其次,要给出评价类内差异的指标离差平方和(Sum of deviation squares,SSD),和反映该种k类分类方式总的差异状况总离差平方和(All-Sum of squares of deviation,ASSD)。最后给出数据集在不同k类划分方式中的评价指标最佳分类优度(The best classification superiority degree,BCSD)。当有一组包含了多种不同类别数据的数据集T,各类别边界划分的具体思路如下。

(1)计算T集合的离差平方和SSD。

(2)

(3)

(4)

(5)

式中,BCSDj为第j组数据的分类优度。BCSD的值在1到0之间。越接近1,分类效果越好;越接近0,分类效果越差。找到BCSD值最大(最接近1)的数据组,即为最佳分类方式。

由于CAT有12个测量探头,只有有限个测量数据。因此,结合反距离权重插值法(IDW)对井眼全截面进行插值预测,结合自然间断点法对插值数据进行2类划分。这种采用自然间断法与反距离权重插值法结合来找出油水边界,并计算平均持水率的方法,简称NB-IDW法,具体思路如下。对井眼横截面进行要素化,各要素在井眼截面均匀分布。①采用反距离权重插值法,利用CAT各探头的归一化响应值计算全截面中各要素的归一化响应值。②采用自然间断点法对井眼要素数据集进行2类划分,得到油水边界值。③根据CAT各探针在纯水和纯油中的归一化响应,对这2类数据进行油水判定(小于0.5的归一化值为水相响应,大于0.5的归一化值为油相响应)。④利用式(6)计算井眼平均持水率。

(6)

2.2.2 基于Java的自然间断点法算法实现

在利用Java进行自然间断点法的油水两相边界划分的算法实现时,考虑到对极大的数据量进行复杂的迭代计算所带来的效率低下问题,在实际编程实现中,采用以下方法实现。

首先,在对井眼横截面进行要素插值后,可以利用Java的Comparator接口构建比较器,然后对所有要素点的归一化数据进行排序处理。

总共有n-1种2类划分的数据组合方式。在对每种2类划分记录了离差平方总和、边界响应值、第1类响应的平均值和第2类响应的平均值后,找出总离差平方和为最小值的分类,并将该分类作为油水两相划分的最优分类。

最优分类的边界值可作为油水两相划分的边界值,这在油水两相中是合理的。当井筒中数据差异不大,或者都接近纯油(纯水)时,这种划分就不太合理。因此,对2类划分中各类别的平均值进行计算,如果低值响应分类的平均值更接近油(平均持率响应<0.5),则判断井筒平均持水率为0;如果高值响应分类的平均值更接近水(平均持率响应>0.5),则判断井筒平均持水率为1(见表4)。这在水平井分层流流型中是合理的。同时,由于流量增大等因素导致的流型变化使得井筒中响应分布发生扰动,也会影响自然间断点分类的结果,针对这种情况需要进一步研究。

表4 基于Java的NB-IDW算法计算结果表(部分数据)

3 算法应用及误差分析

针对水平井油水两相模拟实验数据,基于CAT采用NB-IDW法计算不同流量和含水率条件下的平均持水率(见图4)。

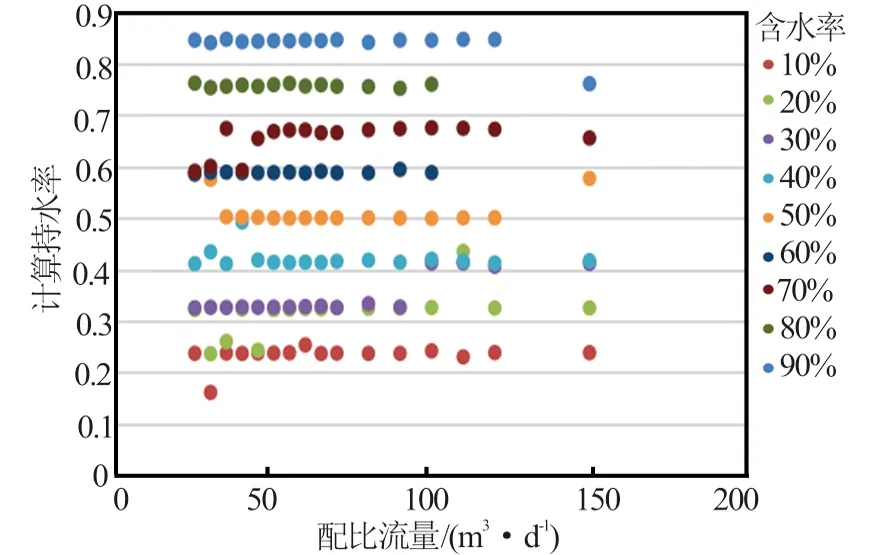
图4 不同流量和含水率条件下基于NB-IDW法持水率计算值

图4中横轴为配比流量,纵轴为计算持水率值,图版模数为该测量点的配比含水率。图4直接反映了在相同流量不同含水率条件下,各持水率测量值与配比含水率的对应关系;同时也反映了不同流量、相同配比含水率测量值与计算持水率的对应关系。从图4中可以看出:当流量低于45 m3/d时,部分流量的持水率计算结果不能很好区分,计算持水率在0.5到0.6之间出现重合。当流量高于45 m3/d,含水率小于30%时,持水率计算结果与实际持水率误差较大;在配比含水率大于30%时,计算效果良好,反映了水平井分层流中不同持水率随含水率的变化。

为了评价在相同配比含水率条件下,对不同流量的持水率计算效果。计算了各含水率中不同流量持水率数据集的标准差。再将不同含水率的标准差绘制成图(见图5)。从图5可知:在配比含水率低于20%(含)时标准差较高,说明测量值离散程度越大,测量稳定度越低;在含水率大于20%时,标准差较含水率为20%以内的更低,说明测量稳定度高,较为可靠。

图5 基于NB-IDW法在各含水率中的测量标准差

从图4和图5可以看出,含水率较低或流量较低时出现的测量误差较大,其原因可能有2个方面。①油水两相中,持水率是水相横截面积与模拟井筒总横截面的比值,其数值大小与油水液面高度相关。油水液面高度与油水流量配比以及井斜有关。在该实验中,井斜固定为水平90°。流体含水率配比主要表现在井筒中水相和油相的流速差异上,且液面高度在圆形截面上随着含水率增加呈现先快后慢再快的变化规律。当总流量较低时,不同含水率的油水速度差异总体较小,液面高度随着含水率增加而增加,液面光滑。当总流量较大,不同含水率的油水速度差异大,液面高度随着含水率增加而迅速增加,液面出现液滴夹带和波动的现象。再考虑到电容阵列持水率仪12个探针等间隔30°分布在井筒截面上,这必然在60°夹角范围内大概率只有一个探针分布。因此,在低流量且含水率小于等于30%时,液面高度变化可能并没有被更多探针测量到,因此,导致了测量值的重合,出现测量误差。当含水率处于50%～70%,液面高度变化小,也不能被更多探针探测到,从而导致测量值重合。②仪器进入井筒中很可能发生了随机旋转,这种旋转会导致探针在井筒中的分布变化,从而改变了可测范围,导致在一定含水率范围内出现测量误差。

为了对实验数据范围内基于NB-IDW法持水率计算值的总体误差进行评价,以关井持水率为依据,绘制了对角线图评价持水率计算值与关井持水率的关系图(见图6)。

图6 NB-IDW法计算持水率与关井持水率关系图

4 结 论

(1)通过物理模拟实验,采用CAT阵列持率仪进行数据采集。在水平井油水两相流条件下,实现了NB-IDW法进行持水率计算和油水边界划分。

(2)在水平井油水两相分层流条件下,采用NB-IDW法实现油水边界的最优划分和持水率计算,具有良好的准确性和稳定性,但在配比含水率低于30%和流量低于45 m3/d时测量存在较大误差。