有效夹紧长度对钢板弹簧力学特性影响分析

0 引言

钢板弹簧是汽车非独立悬架中应用最广泛的一种常见的弹性元件，由若干片合金弹簧片组合而成的一根近似等强度的弹性梁，具有结构简单,质量轻，制造容易，价格便宜，维修方便,工作可靠和承载能力强等特点被广泛应用在轻型货车、小微型客车及某些越野车悬架上

，同时兼有弹性元件、导向机构和减振器作用，如图1钢板弹簧的典型结构，可以保证车轮相对于车架的运动特性，并传递在车轮和车架之间的力和力矩, 并缓和由路面不平传给车架的冲击载荷，衰减由此引起的承载系统的振动，以保证平顺地行驶，对整车行驶的安全性、平顺性和操作稳定性具有重要的影响，刚度与强度是其重要的力学特性，准备获得这些参考的具有重要的意义。

钢板弹簧刚度特性一般呈非线性，具有较稳定的固有频率，从而使汽车有较好的行驶平顺性，这种弹簧包括主簧和副簧：当载荷较小时，只有主簧起作用，刚度为定值；当载荷达到某一定值 P1后，主簧和副簧开始接触，副簧开始起作用，随着载荷逐渐加大至P2，主、副簧接触范围逐渐加大至完全接触，这一阶段刚度逐渐增大；之后两者结合成一体，共同承载，刚度又保持不变。载荷在 P1至 P2区段时，板簧具有渐变的非线性弹性特性，图2钢板弹簧刚度特性曲线示意图。

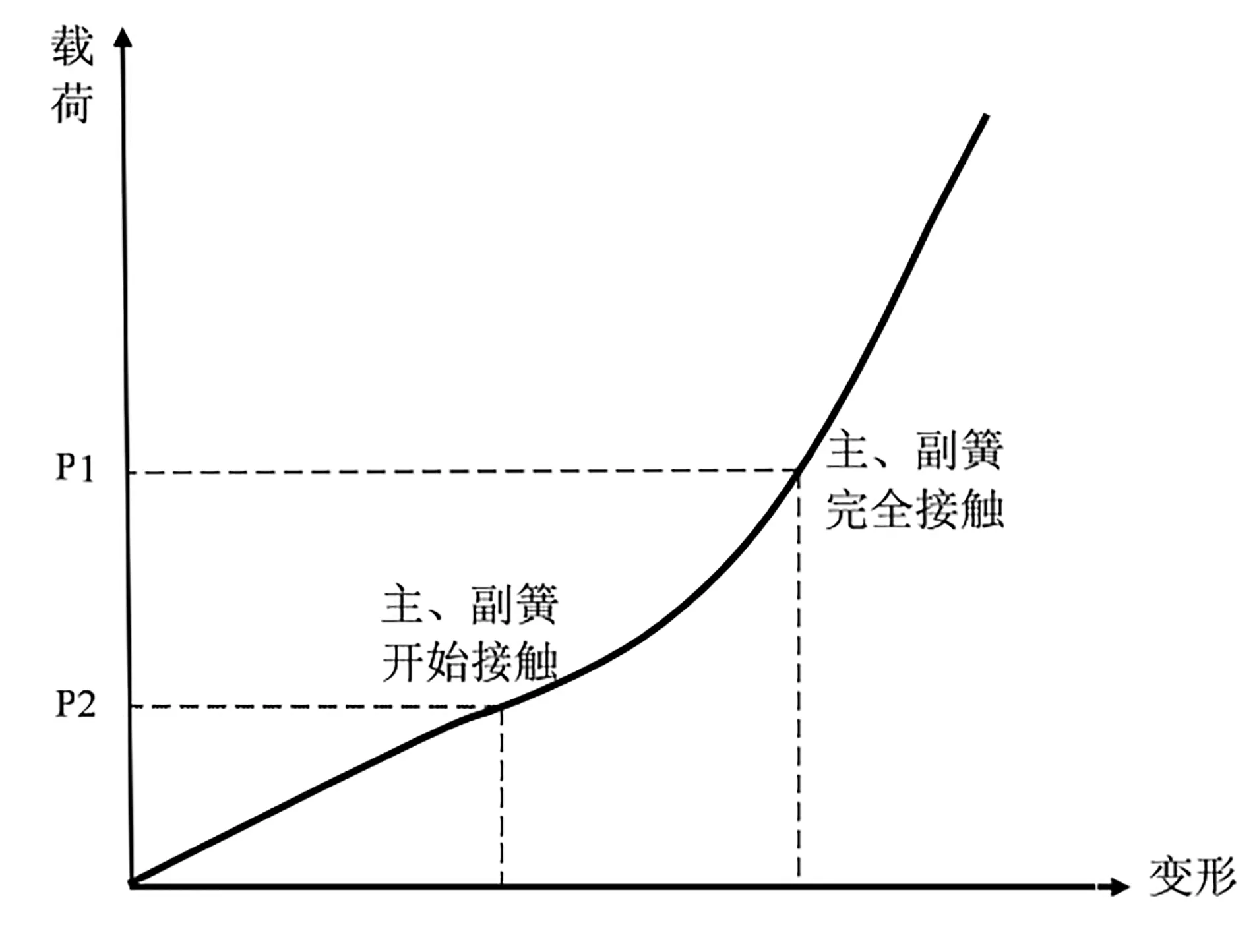
近年来，随着计算机技术的快速发展和普及，有限元方法迅速从结构工程强度分析计算扩展到几乎所有的科学技术领域，成为一种丰富多彩、应用广泛并且实用高效的数值分析方法，钢板弹簧在理论计算为了得到较为准确的数值解，在理论算法上存在各种假设，目前钢板弹簧的理论设计主要有两种算法，共同曲率法和集中载荷法。共同曲率法假设钢板弹簧在任何载荷下，钢板弹簧各片彼此沿整个长度无间隙接触，同一截面上各片具有相同的曲率，从而简化为梯形单片弹簧进行计算。集中载荷法假定在任何负荷下，各叶片间只在端部和根部无摩擦地接触并传力，工作中各接触点不脱开，相邻两片在接触点具有相同挠度。

而有限元方法不需要任何假设就可以得到高精度的结果，与传统的解析方法相比，具有理论上严密、力学模型统一和精度高等优点，本文主要研究不同的夹紧长度对钢板弹簧刚度与强度特性影响，建立某一主机厂的钢板弹簧自由状态的几何模型，考虑夹紧长度的影响

，在ABAQUS里面建立钢板弹簧有限元模型，分析不同的夹紧长度下对钢板弹簧刚度与强度进行分析，并分析夹紧长度对力学特性影响规律，研究结果可以为钢板弹簧刚度与强度的设计提供理论计算，从而大大地缩短调试周期，降低成本，找到最合理的设计方案，达到节省成本、提高开发效率，缩短开发周期的目的。

1 钢板弹簧有限元分析

钢板弹簧在实际工作过程中钢板弹簧产生大变形，属于几何非线性问题；同时叶片间存在接触，接触状态与多种因素相关，属于典型的边界条件非线性问题，因此，钢板弹簧计算中的强度和刚度计算分析是一个包含复杂接触关系、几何非线性分析问题，钢板弹簧有限元分析的准确性与其工作的状态有密切的关系，钢板弹簧总成是通过中心螺栓将不同曲率的簧片装配而成，在装配过程中各片簧间必然产生摩擦,进而产生接触力,使得各片簧上产生一定的预应力,然后通过U型螺栓的作用，将上夹板、下夹板与钢板弹簧装配到后桥上。

1.1 几何模型

图5～7为行程145mm下，钢板弹簧在不同夹紧长度下的等效应力云图，由云图可知板弹簧在承受145mm行程条件下，夹紧长度取88mm、70mm、50mm时，对应的等效应力为1006MPa、1103MPa、1196MPa，应力最大部位主要出现在U型螺栓夹紧区域，且应力云图分布基本一致，但是随着夹紧长度的增加，钢板弹簧的最大等效应力增加，主要原因是在相同受力，惯性矩、扰度情况下，夹紧长度小的根部的应力也小，这与理论是符合的，还可以得出，夹紧长度的改变对整个板簧的应力影响并不大。

1.2 材料属性

钢板弹簧采用各向同性的线弹性材料为60Si2Mn的弹簧，材料特性为：弹性模量为2.06×10

Pa，泊松比为0.3。

1.3 网格划分

为了验证夹紧长度对强度与刚度的影响，仿真过程中,设置夹紧长度分别为上夹板的有效长度88mm(上夹板有效长度),70mm, 50mm (U型螺栓跨距一半),按上述加载形式进行计算，从等效应力与刚度方面研究夹紧长度对钢板弹簧力学特性的影响夹紧长度对等效应力的影响。

2013年，广东省水利厅党组高度重视水政监察工作，多次了解水政监察工作的任务职能，并要求水政监察队伍要严于职守、依法行政。广东省水政监察队伍在各级水行政主管部门的领导下，按照“忠诚、为民、科学、务实”的新时期广东水利人精神，狠抓执法能力建设，认真做好执法查处工作，为维护广东省正常水事秩序、保障水利改革发展发挥了重要作用。

而“东风破”作为一种曲调，出于宋代“曲破”一说。“东风破”可以算作典故的使用，意在使歌曲更加古色古香。

发放问卷60份，回收问卷60份，有效率100%。结果显示实验组学员在提升临床思维分析能力、语言表达能力及自学能力、激发专业学习兴趣、发现和处理问题能力及团队协助意识方面更有优势（表1）。

(2)单元类型：考虑到板簧计算的精度

，单元类型采用单元非协调模式C3D8I,可以有效防止沙漏问题，单元的大小取板簧厚度尺寸的1/3，采用用映射体网格的方式对板簧和上下夹板划分网格。

1.4 接触处理

要进一步强化对财务预算，这样就可以有效的杜绝一些不必要的成本。国有企业在预算管理时要特别注重对预算的监督，以此来实现对生产的监督。要根据国家制定的相关政策来制定，然后根据自身的情况进行完善。要根据对资金的监管，以此来提升对资金的使用效率，以此来实现对财务预算的监督，从而实现资金的使用效率，从而确保预算管理目标的实现，这样就能够实现资金支撑成本的监管。

1.5 模型的约束与加载

板簧的约束与加载来源于板簧的装配加载过程与实际使用工况

，钢板弹簧装配前各片弧高是自由状态，因此在加载前要模拟板簧装配过程，装配加载过程为应用中间螺栓夹紧具有不同曲率和初始弧高的单片，夹紧过程为短片的曲率半径变大，而长片的曲率半径变小。最后各簧片的中间相互紧密贴合在一起，发生接触，即各簧片之间间隙为 0，本文计算模拟装配过程，在第一片簧片的加载头上施加压方向垂直位移，位移大小等于各叶片自由状态下各簧片之间的间隙之和，夹紧模型中上片地面中央节点和下片上面中央节点之间的距离之和36mm，约束上夹板的六个自由度，在上下夹板夹建立连接单元施加位移，该位移为各簧片间隙之和，为了能在台架试验反应板簧的应力水平，添加钢板板簧工作的最大行程，该行程加载在上夹板上，然后在两耳中心点处分别建参考点，耦合内表面，在参考点上约束除水平移动与耳轴旋转自由度外的自由度，如图4钢板弹簧有限元模型。

2 夹紧长度对强度的影响

网格划分是有限元模型建立中一个非常重要的部分,网格划分的好坏对有限元分析计算的结果和精度影响很大,为了建立正确的有限元模型,需要遵循以下网格划分的原则

：

(1)网格数量: 根据有限元理论可知，对同一个分析对象，单元划分越细，对实际结构的模拟越精确，但单元划分过细，即生成的单元数量过多，则计算时间会大幅度增加，考虑精度与计算时间的平衡,网格划分采用纵、横方向尺寸取5mm大小网格。

钢板弹簧簧片间的接触力是通过簧片之间的摩擦产生的

，abaqus是通过在相邻簧片间建立面与面接触来模拟簧片间的接触关系，需要考虑接触面间的摩擦行为，设置接触属性切向摩擦系数为0.1～0.2，摩擦系数较大会造成收敛问题，法向设置成面接触后再分开，接触方式采用面与面的接触分析，接触对由主面与从面，为了防止从面的节点不能穿透主面，一般选面积大的表面作为主面，面积小的表面作为从面，选择有限滑移(finite sliding)来描述接触对间的相对滑动，该钢板弹簧定义了6个接触对，生成后的接触单元。

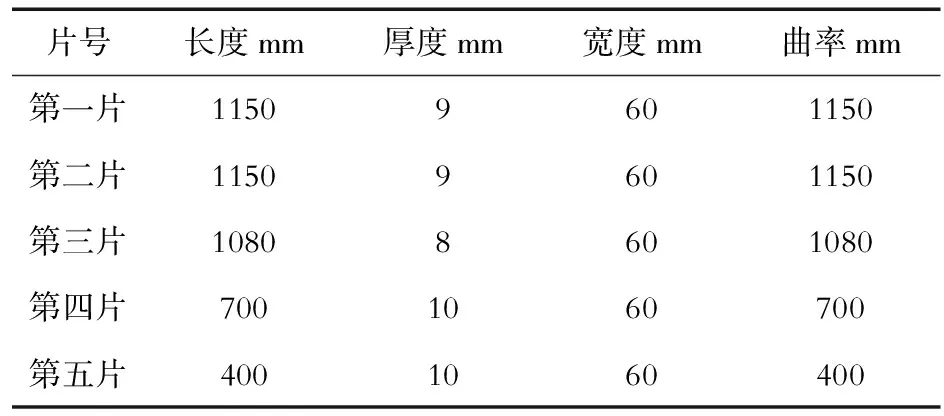
该板簧由5片组成，各片的初始几何尺寸如表所示，各簧片采用自由状态的曲率，出于简化的目的，建模时没有考虑弹簧模型的中心孔、倒角、尼龙垫片以及夹箍、铆钉等连接件，可以大大减少计算量，且对钢板弹簧实际应力影响较小，如图3

3 夹紧长度对刚度的影响

钢板弹簧是一种非线性弹簧，由主簧和副簧组成，当载荷较小时,只有主簧工作；当载荷超过一定限度后，副簧与主簧开始接触，随着载荷逐渐增大，副簧与主簧完全接触，此时钢板弹簧刚度也逐渐增大，刚度特性呈非线性，即副簧刚开始接触的主簧刚度与完全接触的合成刚度。

1.2 对脑的作用 肠道菌群影响脑的活动甚至行为。肠道菌群调控脑和行为的机制涉及多方面,包括肠道神经系统、神经影像学、肠道菌群和宿主的相互作用以及肠道菌群-肠-脑轴。肠-脑轴是肠和脑之间的信息交流系统,肠道菌群在肠道菌群-肠-脑轴中主要通过免疫、迷走神经和神经内分泌途径来行使功能。

根据仿真的结果可以得到不同夹紧长度下该钢板弹簧位移与刚度的特性曲线图8，由表2数据可知随着夹紧长度的增大，夹紧刚度也增大，当主片簧伸直长度相同时，夹紧长度越短，悬臂的长度越长，变形越大，即刚度越小，这与实际力学现象是一致的，如果夹板有效长度取的太长，对刚度的影响很大，建议采用U型螺栓跨距一半作为衡量板簧计算的规范，这样有利于与理论对比，才能知道刚度算的靠不靠谱，才能进行后面的强度分析，同时这里也为我们的设计提供了指导，夹紧长度的增大有助于刚度的提升，但随之而来的等效应力为增大，所以要权衡解决。

4 结论

1)通过有限元对钢板弹簧夹紧长度对强度的分析，可以得到随着夹紧长度的增加，钢板弹簧的最大等效应力增加，但夹紧长度的增加对整个板簧的应力影响并不大。

2)通过有限元对钢板弹簧夹紧长度对刚度的分析，可以得到随着夹紧长度的增加，钢板弹簧的刚度也增加，但夹紧长度的增加对整个板簧的刚度影响较大。

3)利用有限元软件分析可以缩短产品的开发时间，降低开发成本，保证产品的质量，具有十分重要的意义。

[1]余志生.汽车理论[M]. 北京：机械工业出版社，2009:108-109.

[2]王望予.汽车设计[M].北京：机械工业出版社，2003：166-167.

[3]成大先.机械设计手册[M]，化学工业出版社，2004.7-11-7-13.

[4]陆志成等. 某车钢板弹簧刚度分析[J]. 汽车科技，2011,6:56-58.

[5]蒋立盛.渐变刚性钢板弹簧的计算方法.汽车技术，1983， (11)： 14-20.

[6]石亦平.ABAQUS有限元分析实例讲解[M]. 北京：机械工业出版社，2006.

[7]张胜兰等.基于hyperworks的结构优化设计技术[M]. 北京：机械工业出版社，2008:87-120.

[8]李刚. 渐变刚度钢板弹簧后悬架有限元与动力学建模及仿真[D]. 长春：吉林大学，2011.14-16.

[9]张英会. 弹簧手册[M]. 北京：机械工业出版社，2009.545-555.

[10]于安和，桂良进，范子杰.钢板弹簧刚度特性的有限元分析[J].汽车技术，2007.2.