考虑保理融资的电商供应链网络均衡模型

李永华，陈兆波，姚锋敏

(1.哈尔滨理工大学 经济与管理学院, 黑龙江 哈尔滨 150080；2.太原科技大学 经济与管理学院，山西 太原 030024)

0 引言

2015年，京东突然单方面要求其供应商(大部分为中小微企业)将原有合同中约定的45天账期延长至60天，这给上游的众多中小微企业带来了巨大的资金压力。此外，电商平台的延期付款也为中小微企业带来了其他一系列的问题，如需要专门的员工或机构来管理应收账款、应收账款占压会产生时间成本等。因此，这些中小微企业迫切需要有效的方法来释放应收账款占压的现金流，其中保理就是一种非常有效的途径。

保理是一种由保理商提供的包含资金融通、应收账款管理、信用风险担保等一系列服务的综合金融服务方式[1]。大多数情况下，保理是卖方将其与买方订立的货物销售/服务合同所产生的应收账款转让给保理商，以满足其未来或当前的资金需求。近年来，全球保理业务量以平均每年9%的速度增长[2]，并且保理的服务对象主要为中小微企业。

在这些实践背景下，本文旨在回答以下两个问题：①在竞争环境下，中小微企业采用保理融资的动机是什么；②电商平台的延期付款时间是如何影响中小微企业的保理融资决策的。本文考虑由多个中小微企业和多个电商交易平台组成的供应链网络系统，中小微企业生产差异化的季节性产品，并通过电商平台直接销售给消费者，同时向电商平台缴纳一定的技术服务费。中小微企业之间从事非合作竞争，并根据电商平台的延期付款时间来确定产出和保理融资策略。本文将保理融资引入供应链网络，利用变分不等式的方法构建了供应链网络均衡模型，分析了延期付款时间对供应链网络运营和中小微企业保理融资决策的影响，并提出了一种求解供应链网络模型的有效算法。

1 文献综述

本文主要涉及供应链运营和金融的交叉领域以及供应链网络领域的研究。

XU等[3]最早将资金约束企业的融资问题与运营管理相结合，并指出在市场需求不确定的环境下，当破产成本存在时，有必要进行运营和融资的联合决策。随后，如LAI等[4]，KOUVELIS等[5]，DADA等[6]，YANG等[7]，YANG等[8]分析了不同的融资方式在缓解供应链资金约束中的有效性。在诸多融资方式中，交易信用是供应链运营过程中经常采用的融资形式，受到了学术界的广泛关注。一般来讲，交易信用将市场风险向边际成本更低的主体转移而创造新的价值，从而提高供应链的运营效率。然而，当中小微供应商在提供交易信用时，常常会因为应收账款管理、资金占压等问题为企业自身运营带来不利的影响，中小微供应商解决该问题的一种方法是将应收账款转移给保理商。

近年来，大量研究从运营和融资的视角来分析保理对供应链绩效的影响。TANRISEVER等[9]讨论了采用反向保理策略时，供应链成员的运营和融资决策，并分析了影响保理价值的相关要素；WUTTKE等[10]分析了自有资金和采购量对保理融资以及延期支付时间的影响；LEKKAKOS等[11]发现供应商在采取反向保理时，通过确定合适的库存策略，可以获得更有利的融资利息，并实现10%以上的营运资本节约；TUNCA等[12]认为，与低效的传统供应商融资相比，反向保理可以获得较低的批发价和较高的订单数量，并显著提高供应链绩效；KOUVELIS等[13]建立了一个拉式结构的供应链模型，发现追索权和无追索权保理的优势主要取决于供应商的信用评级、现金投资回报率和延期付款时间；张晓建等[14]在存在破产成本的前提下，根据无追索权和有追索权保理模型及相应算法，研究了供应链企业中零售商、供应商及保理商的融资策略；林强等[15]构建了信息不对称下的供应商与制造商的委托代理模型，并用数值算例对比验证了保理融资模式优于普通直接贷款模式；于辉等[16]通过单周期报童模型，研究了订单转保理模式对供应链效率、零售商收益等的影响；潘福越等[17]、林强等[18]分别在保理融资模式下，设计了供应商—制造商两级供应链的收益共享契约和数量折扣契约模型，通过理论证明了在需求具有价格敏感性时，这些契约对供应链具有协调效果；顾超成等[19]在确定性需求的假设下，从制造商的视角对比分析了在有限时域内，固定期保理和即时保理两种策略的优劣；任龙等[20]研究了中小外贸商在面临需求风险和外汇风险时，如何通过保理决策为企业带来价值；李苜等[21]基于市场需求随机波动，将违约风险引入保理融资期望收益模型，分析了不同风险水平下保理策略对供应链上下游企业的决策及收益产生的影响。

虽然上述文献已经研究了保理的许多方面(如保理对供应链绩效的影响、保理合同条款的确定)，然而，上述研究主要集中在由单一供应商和单一零售商构成的供应链系统，供应链的结构较简单。随着经济的发展，供应链的结构越来越复杂，网络化趋势越来越明显。因此，本文在由多个中小微企业和多个电子商务平台构成的供应链网络中分析企业的保理融资决策，期许为中小微企业的发展提供一些有益的见解。

与微观模型研究相比，一些学者试图从宏观的角度对供应链成员企业之间的相互作用进行分析。此类研究的主要特点是针对由多个节点企业构成的一般化网络模型，利用变分不等式的方法分析供应链成员企业的均衡策略。例如，NAGURNEY等[22]提出了一个三层供应链网络均衡模型，并利用有限维变分不等式描述了成员企业的均衡条件；随后，CHENG等[23]、WAKOLBINGER等[24]、CHEN等[25-26]、NAGURNEY等[27-28]对供应链网络模型进行了一系列的扩展研究。然而，上述研究大多忽略了供应链网络成员的资金约束问题，尤其是保理融资问题，因此本文在供应链网络的统一框架下分析中小微企业的保理融资决策。

2 模型描述及符号定义

考虑一个由m个中小微企业和n个电商交易平台构成的供应链网络，其中m个中小微企业负责生产不同的季节性产品，并通过n个电商交易平台(如京东、天猫)将产品直接销售给消费者，用i表示第i个中小微企业供应商，i=1,2,…,m；用j表示第j个电商交易平台，j=1,2,…,n。 为了简便，本文将中小微企业i生产的产品表示为产品i，电商平台j对应的需求市场也表示为j。 假设决策期为T，并且每个中小微企业在[0,T]内仅有一个生产机会。不失一般性，本文忽略产品生产期，且产品销售季开始于0，结束于ts。 平台j的延期付款期为tj，且T>max{ts+tj,j=1,2,…，n}，用t表示所有tj构成的列向量。事件的时间顺序如图1所示。

在0时刻，电商平台j宣布其延迟付款期tj并公布其需求预测信息。同时，每个中小微供应商准备生产资金并决定其产品产出量。中小微供应商在ts+tj时刻获得平台j支付的销售款。然而，在ts时刻，中小微供应商获得一个新的投资机会，此时需要决定是否采取保理融资策略。

2.1 供应链网络的运作

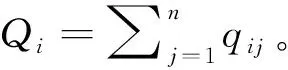
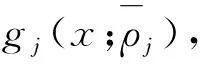
市场j中的消费者考虑从产品集合中购买一单位的产品，本文假定消费者的选择过程服从Logit模型[29]，模型基本形式如下：令Uij为产品i通过平台j销售的消费者效用，Uij=ui-ρij+εij，其中：ui是一个常数，εij是服从均值为零的Gumble分布的随机变量。用Prij表示消费者在电商交易平台j上选择产品i的概率，则

(1)

因此，dij(市场j对产品i的需求)的需求分布函数可表示为

(2)

本文假定中小微供应商完全承担产品的库存风险。例如，京东规定供应商在两周内如果缺货率超过1%，京东将收取缺货费。不失一般性，本文忽略销售季结束后未售出物品的残值。

2.2 中小微供应商的保理融资决策

对应交易平台j的应收账款将在ts+tj到期，但是中小微供应商在ts时刻有一个新的投资机会。不失一般性，本文假定中小微企业在ts时刻的现金为0。因此，中小微供应商若希望抓住这个投资机会，则需要进行短期融资。假设保理是中小微供应商可以采用的唯一融资渠道，因此每个中小微供应商在ts时刻都需要决定是否采取保理融资。

定义二进制变量λij为中小微企业i的融资策略。λij=1表示中小微供应商i决定把对电商平台j的应收账款卖给保理商，并在ts时刻立即拿到现金；而λij=0表示中小微供应商i继续持有应收账款，直到ts+tj时刻获得现金，此时该供应商丧失再投资机会。因此，中小微供应商i在ts+(1-λij)tj时刻从平台j获得的现金可以表述为：

(3)

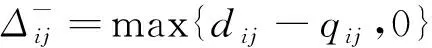
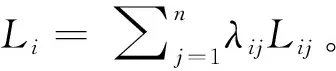
3 考虑中小微供应商保理融资的供应链网络均衡模型构建

3.1 中小微供应商的均衡条件

根据电商平台发布的延期付款期和需求预测信息，每个中小微企业将独立地确定各自的生产、销售和保理融资计划，以最大限度地提高决策期内的期望利润。因此，中小微供应商i的最优化问题可表述如下：

(4)

式中：πi为中小微供应商i的利润函数，r为闲置资金的银行利率。

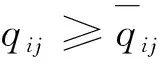
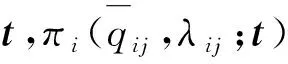
证明若λij=1，即中小微供应商i将电商交易平台j的应收账款卖给保理商，由于Φi(L)是关于Li的递增凹函数，且fi是关于qij凸的，根据式(4)，可以得到：

因此，当λij=1,时引理1成立；同理可以证明,当λij=0时,该结论依然成立。

定理1若假设1成立，对任意给定的λ和t，当且仅当q*由如下变分不等式确定，q*是中小微供应商间的纳什均衡：

(5)

证明对于任意给定的λ和t，根据凹性和最大化原则，若qij是纳什均衡策略，当且仅当对任意的i=1,2,…,m和j=1,2,…,n，

(6)

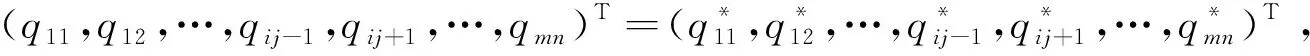
均衡条件式(5)有一个很好的经济解释。对任意给定λ和t，当且仅当中小微供应商i的边际收益等于相应的边际生产成本时，中小微供应商i才会在电商交易平台j上销售产品。

3.2 市场的均衡条件

对于中小微供应商i生产的产品和电商交易平台j，i=1,2,…,m，j=1,2,…,n，市场需求的均衡条件可以表示为如下形式：

(7)

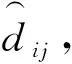
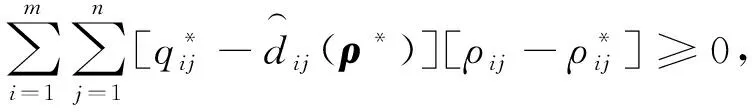
(8)

3.3 考虑中小微供应商保理融资策略的供应链网络均衡模型

对任意给定的t和λ，所有中小微供应商之间相互博弈达到均衡时，M变分不等式(5)和市场均衡条件(8)需同时满足。因此，考虑中小微供应商保理融资策略的供应链网络均衡模型可以用如下定理描述。

定理2若假设1成立，则

(1)对于任意给定的t和λ，考虑中小微供应商保理融资策略的供应链网络均衡条件等价求解(q*,ρ*)，使其为如下变分不等式问题的解：

(9)

(2)对任意给定的t和λ，至少存在一个(q*,ρ*)满足变分不等式(9)。

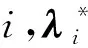
证明

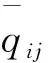
(3)根据上述结论，对于给定λ和t，可以得到中小微企业的均衡产出决策和利润。换句话说，对于给定的t，中小微企业之间的保理策略博弈可以表述为矩阵式博弈，且当没有中小微企业有动机去改变其保理策略时，可获得该矩阵式博弈的均衡策略。

4 求解算法

定理2描述了考虑中小微供应商保理融资策略的供应链网络均衡策略(q*,ρ*,λ*)需要满足的均衡条件，本章将进一步给出求解该均衡策略的算法。为方便，令：

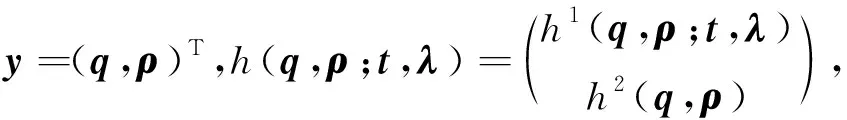
因此，变分不等式(9)可以改写为：对任意的y∈K，求解y*以满足

h(y*;t,λ)T(y-y*)≥0, ∀y∈K。

(10)

目前，常见的求解供应链网络均衡模型的算法主要包括投影算法和欧拉算法等。本文将在给定t情况，给出如下算法来求解包含二元变量λ的均衡解(q*,ρ*,λ*)，具体过程如下：

步骤1将所有λ组合为矩阵P，且λij=1,0。

步骤2对任意的λl∈P，求解式(10)得到(q*,ρ*;λl,t)T，并获得πi(q*,ρ*;λl,t)。

(1)给定y0∈K,δ和ε；

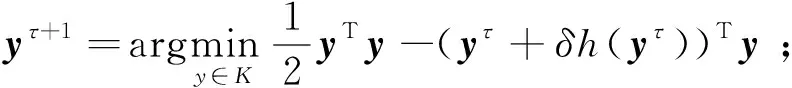
(3)若‖yτ+1-yτ‖≤ε，结束；否则，令τ:=τ+1，转步骤(2)。

步骤3建立收益矩阵πi(q*,ρ*;λl,t)，并通过矩阵博弈求解获得λ*。

5 数值算例

本章将通过数值算例分析电商平台的延期支付期、保理商收取的保理费率以及投资回报对上游中小微企业保理决策的影响。为方便，本文给出一个包括两个中小微供应商、两个电商交易平台的供应链网络进行算例验证。假设决策期T=10，产品的销售期ts=5，供应商生产产品的固定效用u1=u2=30，电商交易平台收取的缺货费率ξ1=ξ2=0.15，两个电商收取的平台费率α1=α2=0.1，且中小微供应商i的投资回报Φ(L)=eυi(T-ts)Li，i=1,2，其中vi为投资收益率。 两个中小微供应商的生产成本函数如下：

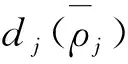
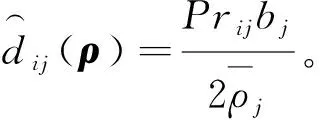
5.1 延期付款期和保理费率对中小微企业均衡决策的影响

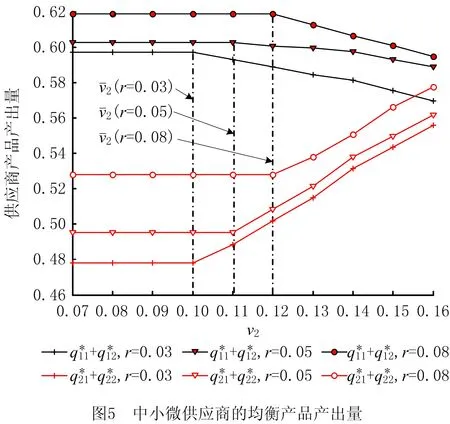
本节将在电商交易平台1的延期付款期t1=1、保理商1的保理费率η1=0.2，闲置资金的无风险利率r=0.05的情况下，分析电商平台2延期付款期t2以及保理费率η2对中小微供应商均衡产品产出量、利润以及保理融资策略的影响。为了分析方便，假设两个中小微供应商的投资收益率vi=0.12，i=1,2。 利用第4章算法来求解该算例，其中利用欧拉算法来求解变分不等式(10)(其中：δ=0.005,ε=0.01)。中小微供应商的均衡产出量以及企业的均衡利润如图2～图4所示。

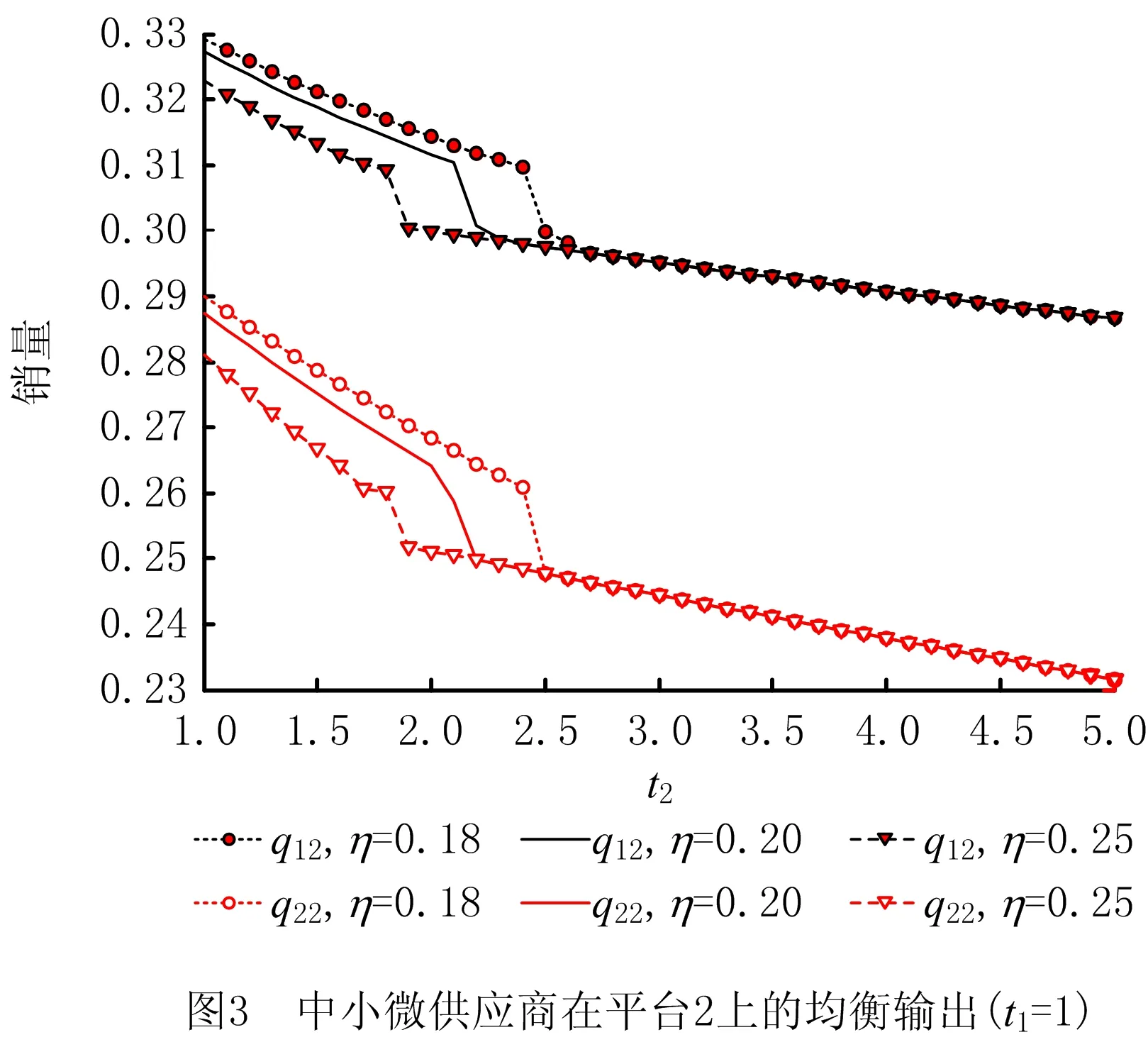
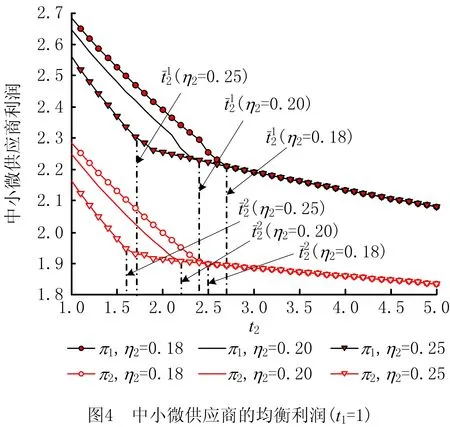
根据图2～图4的均衡结果，可以得到以下结论：

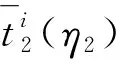
5.2 投资收益率对中小微企业均衡决策的影响

本节将在两个电商交易平台的延期付款期均为3、保理费率η1=η2=0.15的情况下，分析投资收益率对中小微供应商均衡产品产出量、利润以及保理融资策略的影响。为方便分析，假设供应商1的投资收益率v1=0.12，其余参数与5.1节算例相同。利用第4章给出的算法，中小微供应商的均衡产出量以及企业的均衡利润如图5～图7所示。

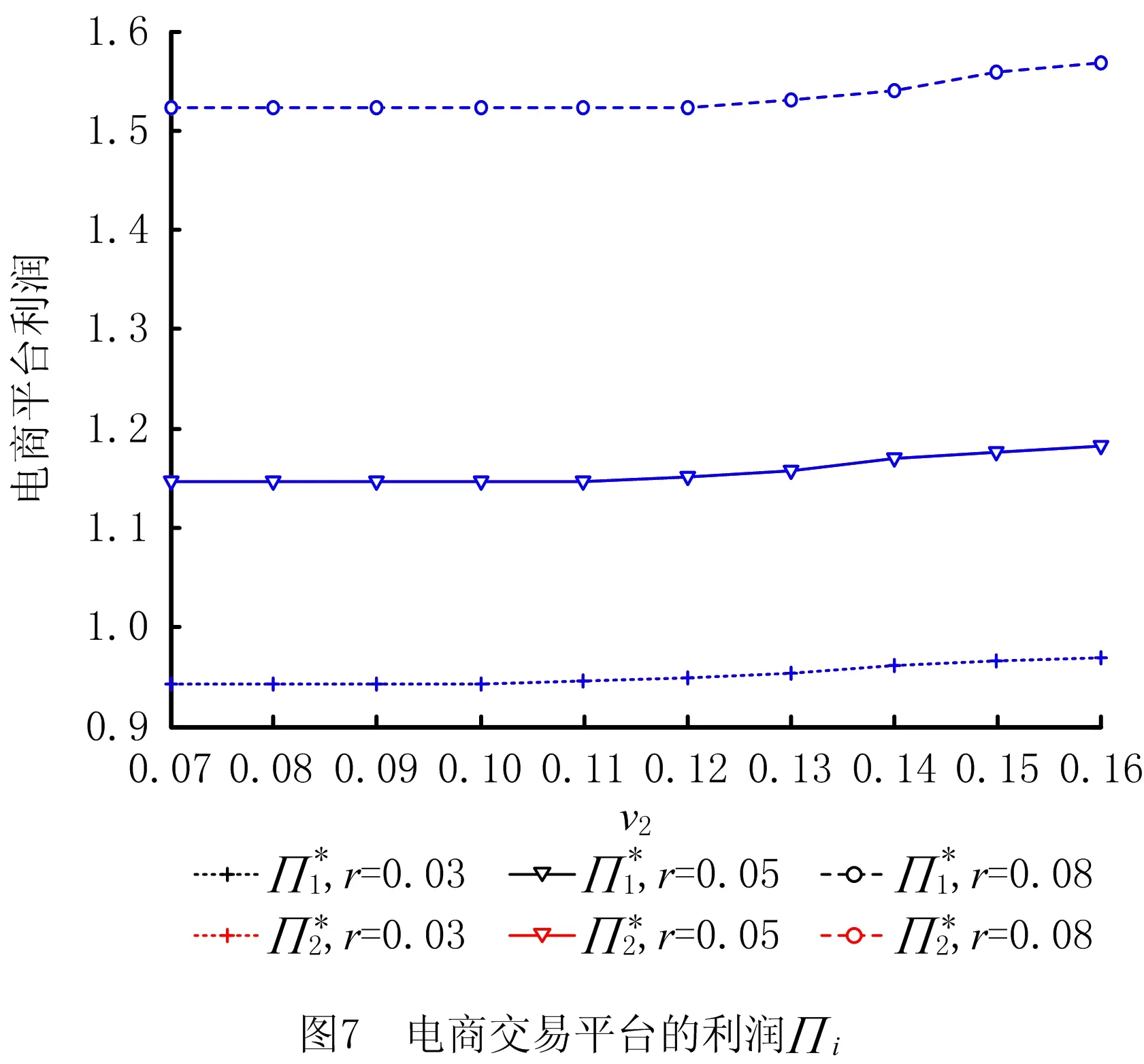
根据图5～图7的均衡结果，可以得出以下结论：

6 结束语

本文将保理融资引入由多个中小微企业和多个电子商务平台组成的供应链网络系统，利用变分不等式的方法构建了考虑保理融资的电商供应链网络均衡模型，分析了电商平台的延期支付对上游中小微企业的运营和保理决策的影响，且提出了一种结合欧拉算法和矩阵博弈求解相结合的有效算法。得到以下主要结论：①电商平台的延期付款期会降低中小微企业的产品生产量及其利润；②只有当延期付款期在一定的临界值内，中小微企业才会选择保理融资，否则中小微企业会选择持有应收账款，并且保理费率是影响该延期付款临界值的一个重要因素；③投资收益率和银行的无风险利率对供应商应收账款的保理融资策略具有非常重要的影响作用。因此，中小微供应商在决定是否进行应收账款保理时，需要综合考虑保理商收取的保理费率、应收账款的延期支付期和资本再投资的收益率等因素。由于本文考虑的是信息对称下的供应链网络系统，未来可将该模型可扩展到信息不对称的情形。