基于RRCD和RADPD的机场消防站多目标选址模型

贺元骅，李 想，熊升华，陈振颂，伍 毅

(1.中国民用航空飞行学院 民航安全工程学院，四川 广汉 618307;2.武汉大学 土木建筑工程学院，湖北 武汉 430072)

0 引言

随着经济的发展和民航技术的提升，飞机逐渐成为人们远途出行的首选方式。机场流量的增加，给机场消防安全保障带来了前所未有的挑战。机场消防站是设立在航空器活动区适当位置，具有相应的消防设备，承担发生在机场或其紧邻地区的航空事故或航空器地面事故及其他消防救援任务的机构[1]。当机场消防站处于最佳位置时，不仅能够有效地降低出警时间，还能显著提升机场应急救援保障能力。目前，民航机场消防站选址主要存在以下实际问题：既有行业标准中对机场消防站选址的具体规定偏少，《民用航空运输机场飞行区消防设施》(MH/T7015-2007)5.4建议机场消防站宜靠近跑道或滑行道中部[2]，但该建议不一定能够满足机场实际消防需求；机场建设和运行过程中往往根据机场其他设施的布局设置机场消防站；很多机场并未考虑机场消防救援路线的拥堵程度及跑道事故分布等对机场消防站选址的影响。鉴于此，本文主要针对机场消防站选址优化问题开展相关研究。

消防站选址和布局是提升消防站救援效率的直接手段，也是提升消防应急能力的重点研究问题之一。目前，有关消防站选址和布局的研究主要涵盖城市[3-4]、化工园区[5-7]、机场[8-12]等领域。针对机场消防站选址，TZENG等[8]从成本、消防站数量等因素考虑机场消防站的选址，提出一种模糊多目标模型，以确定消防站的最佳数量和位置，但论文模型的最佳精度适用于3个及3个以上的消防站；郝爱玲[9]阐述了欧美等航空发达国家对机场消防站的相关要求，然而该文献并未研究如何根据机场跑道条件进行消防站最优选址；胡栋栋[10]结合图论对机场消防站进行规划，提出了应答时间和最短路径的约束条件，但该文献未考虑机场拥堵程度对消防救援路线的影响；贺元骅等[11]在综述多跑道机场构型基础上，根据机场消防车行驶距离、不同消防救援通道等因素构建消防站选址模型；LI等[12]根据机场每小时航班量和机场每小时航站座位数，利用灰色预测模型预测机场未来拥挤程度，并以此定义正态分布参数，评估机场拥堵程度模型对机场消防站的影响。可以看出，目前消防站的研究重点聚焦于城市和化工园区，而有关机场消防站选址的研究相对较少。此外，既有有关机场消防站选址的研究未考虑机场的拥堵程度和机场跑道实际事故分布等因素，这是本文重点关注的关键问题之一。

随着民航的发展，机场日益繁忙，包括航空器、地面车辆在内都会造成机场拥堵，机场拥堵成为了大中型机场一个亟需解决的问题。针对机场拥堵程度，MARN等[13]构建了代表飞机的地面运动模型，改善飞机在飞机拥堵期间的滑行路线和时间表，但该模型必须连接进离港的航空器和地面控制器；NAVAZIO等[14]构建了一个整数线性规划模型，使航班分配、机场容量、航空公司等各方总延误成本最大限度地减小；RUHL等[15]研究了机场内外的拥挤程度，并建立了数学模型以确定拥堵对机场陆侧设施的影响。由机场拥堵的既有研究可知，日益繁忙的机场会造成拥堵，因而机场消防车在消防救援路线上也不可避免地会产生延误。基于此，本研究将考虑机场救援路线上拥堵程度对机场消防救援效率的影响，构建机场消防救援路线拥堵程度模型。

在整个飞行过程中，起飞3分钟和着陆5分钟是整个飞行阶段中风险最大的时段[16]，且大部分的航空事故都发生在跑道上。为此，研究机场跑道事故点位的概率分布，是提升机场安全性的一个重要环节。针对机场跑道事故发生概率， SALMON等[17]针对无塔台机场，并定义相对危险和绝对危险概念，以此为基础研究了跑道紧邻范围内的飞机事故的概率和次数，以量化机场外部风险；TRUCCO等[18]建立了一个危险概率模型，利用蒙特卡罗方法计算并评估冲偏出跑道的风险，为机场提供一个区域风险图，并利用机场的交通相关因素和天气相关因素对模型进行了修正；许晨晨[19]计算了航空器地面事故风险，并建立了一个概率模型，仿真分析飞行区航空器事故火灾风险点的区域分布特征和月度分布特征，以评估其火灾风险。从目前的研究分析，通过挖掘跑道事故数据，能够找到跑道事故的特殊规律。考虑到机场跑道事故分布对机场消防救援效率的影响，本研究拟对机场跑道事故模型进行探索，以保证消防救援的高效性。

综上所述，本文构建了基于机场拥堵程度和跑道事故离散型概率分布的机场消防站选址优化模型。考虑到我国238个机场(其中单跑道机场222个，多跑道机场16个)大部分机场为单跑道机场(大于90%)，因此本文主要考虑单跑道机场的机场消防站选址优化。首先在民航规章的基础上，建立了机场消防理论救援半径模型；其次考虑机场拥堵程度，建立了机场消防救援路线拥堵程度模型；随后基于跑道事故离散型概率分布，构建了跑道事故离散型概率分布模型；然后，结合上述模型，构建了机场消防站多目标选址优化综合模型；最后，利用实际案例说明了本文所构建模型的合理性。

1 机场消防理论救援半径模型

根据国际民用航空组织(International Civil Aviation Organization, ICAO)《Airport Service Manual Part 1: Rescue and firefighting》[20]及中国民用航空局《民用航空运输机场飞行区消防设施》[2]规定，机场消防车应在3 min内到达事发地点。机场消防车应在25 s内加速至80 km/h，然后加速至105 km/h的最大速度并以最大速度行驶(如图1)。

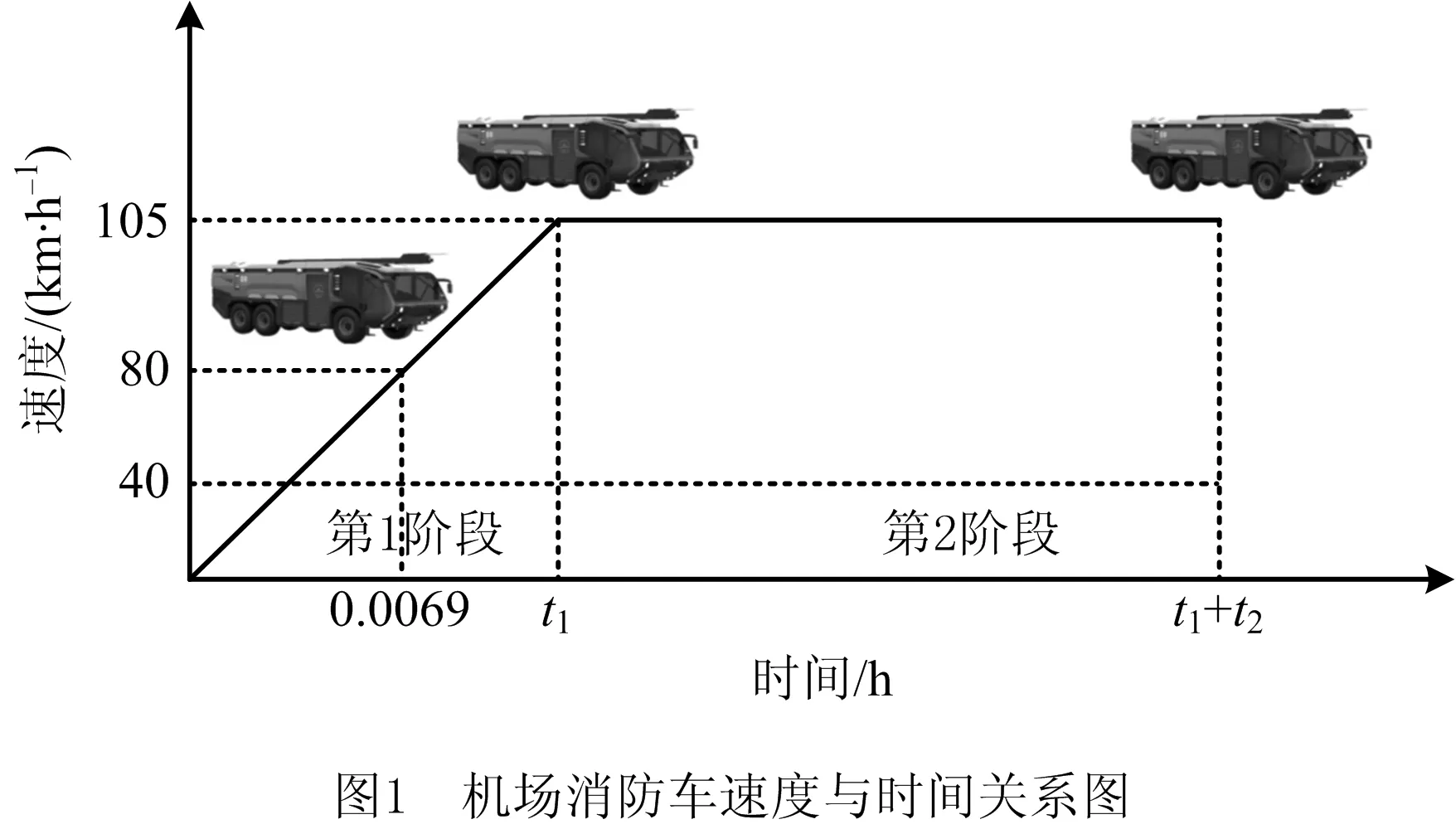
按照中国民航局《民用航空运输机场消防站管理规定》规定，机场消防站执勤人员听到出动信号后，应迅速出动，消防车从接警到驶离车库时间不得超过1 min，即机场消防车需要在2 min内到达事发地点。因此，机场消防车2 min内行驶的最远距离可按式(1)计算。为简单起见，本文假设消防车在加速阶段(第一阶段)做匀加速运动。

(1)

式中：X为机场消防车行驶距离(单位：km)；a为机场消防车的加速度(单位：km/h2)；t1为机场消防车做匀加速运动的时间；t2为机场消防车做匀速运动的时间；v2为机场消防车匀速行驶的速度(单位：km/h)。计算得出加速度为：

a=80/(25/3600)=11520 km/h2。

(2)

同理可得：t1=0.009 1 h，t2=2/60-t1=0.024 2 h。 根据机场消防车2 min内行驶的最远距离，可以确定机场消防车的救援保障半径(不考虑转弯)为3.0215 km。

由于机场消防车的行驶距离由机场消防站到事故发生地点的距离确定，若机场消防车能在2 min内抵达离机场消防站最远的跑道端点进行救援，则机场消防车能够在2 min内抵达机场跑道的任意一个位置进行救援。因而，可将研究问题转换为消防车从机场消防站行驶到最远端点进行救援的问题，即求X(如图2)，图中：S为机场消防站的位置，Z为跑道及跑道附属区域的长度(即机场消防车所需保障区域的长度)。

根据机场消防理论救援半径公式，在救援过程中，机场消防车匀速行驶的时间可表示为：

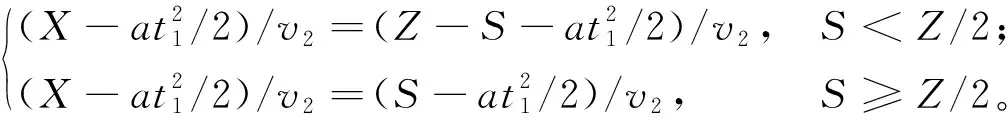
(3)

式中:加速度a、匀加速阶段时间t1已在本章求得，机场消防车最大速度v2已知为105 km/h。为消除量纲差异，合理构建机场消防站选址优化模型，将式(3)进行归一化处理，可得归一化机场消防理论救援半径模型为：

(4)

2 机场消防救援路线拥堵程度模型

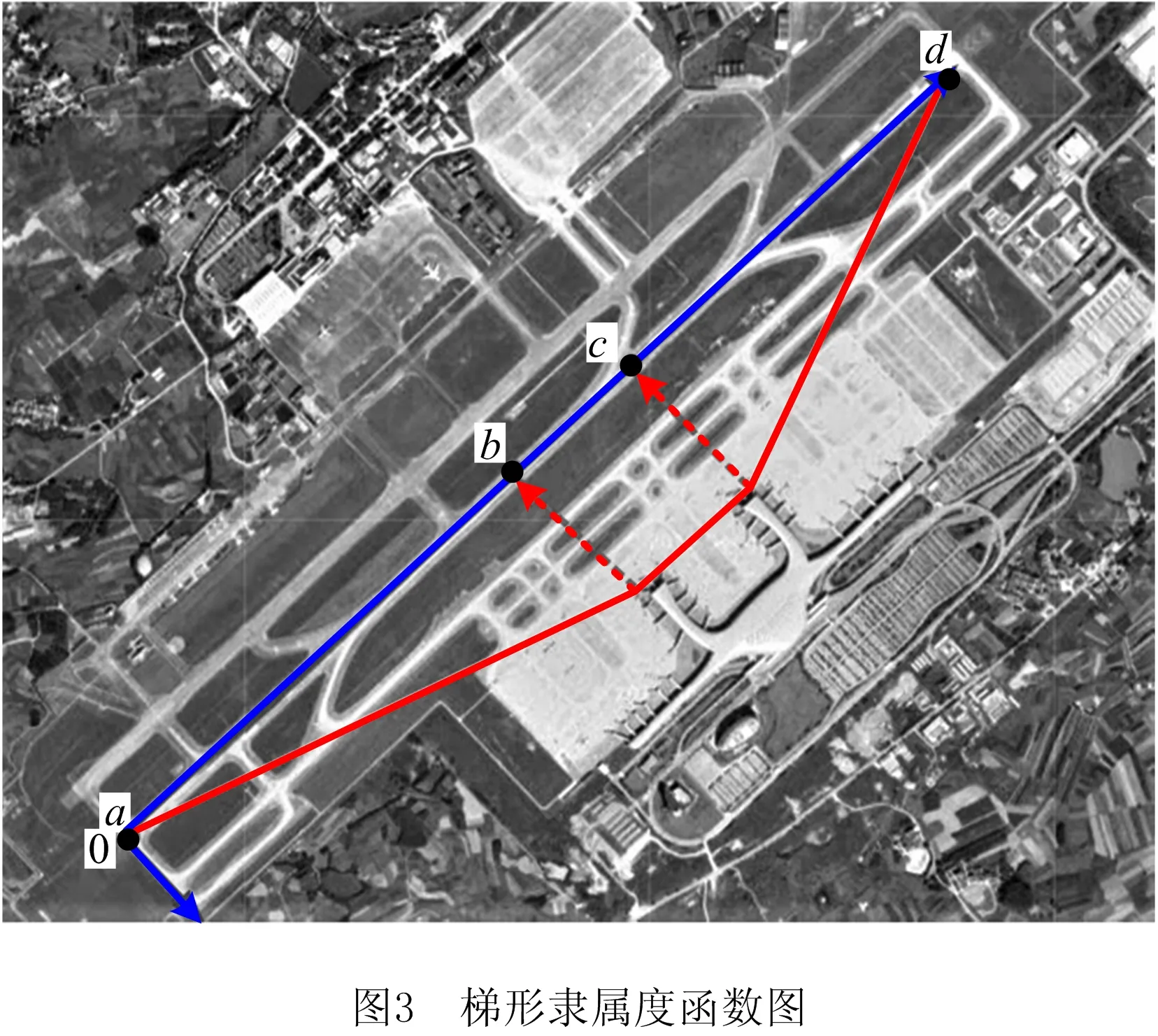
在机场实际运行过程中，越靠近航站楼，情况越复杂[21]，机场消防车在航站楼附近可能无法发挥最佳效率。当机场消防站设置在航站楼附近时，在机场消防车出警的初始路线上，复杂的周边情况可能影响机场消防车的行驶速度。鉴于此，本文引入拥堵程度的概念，即机场消防站越靠近航站楼，该位置上的消防救援路线拥堵系数越高。根据上述描述，本文利用几种常见隶属度函数描述机场消防救援路线拥堵程度理论模型，并给出其参数获取方式，具体如表1所示，各函数对应的图形如图3～图6所示。

表1 机场消防救援路线拥堵程度函数表

需说明的是，机场消防救援路线拥堵程度函数与机场的航班量、旅客量、航站楼位置、运行活动实际分布等因素息息相关。因而，在实际机场消防站选址优化问题中，可结合上述因素，利用统计假设检验、回归分析等方法优化模型参数或直接确定机场消防救援路线拥堵程度函数实际决策模型。综合考虑计算复杂度和决策效果，若未作特殊说明，本文利用表1中的机场消防救援路线拥堵程度理论模型开展机场消防站选址优化研究。

3 跑道事故离散型概率分布模型

起飞或着陆阶段中，大部分航空事故都发生在跑道或者临近跑道一定距离的范围内[16]，为提升机场消防站救援效率，使机场消防站尽可能靠近事故发生概率高的地方，因此本文考虑机场跑道事故离散型概率分布对机场消防站的影响。本文分别在SKYbrary、Bureau of Aircraft Accidents Archives、Aviation Safety Network和Wikipedia等网站搜集了600多例发生于机场及其周边的航空器事故，其中起飞3 min和降落8 min的事故有200多例，记录事故发生具体位置的案例共105起。通过提取跑道事故发生的相对位置，构建跑道事故离散型概率分布模型。因机场消防车救援保障半径有限，根据《民用航空运输机场飞行区消防设施》[2]对应急通道的要求，本文主要考虑发生在机场内，且能够投影到跑道及跑道延长线上的事故，即有效事故，共计71起。因跑道长度不同，本文计算事故发生的相对位置，公式如下：

(5)

所得部分跑道事故相对位置如表2所示。

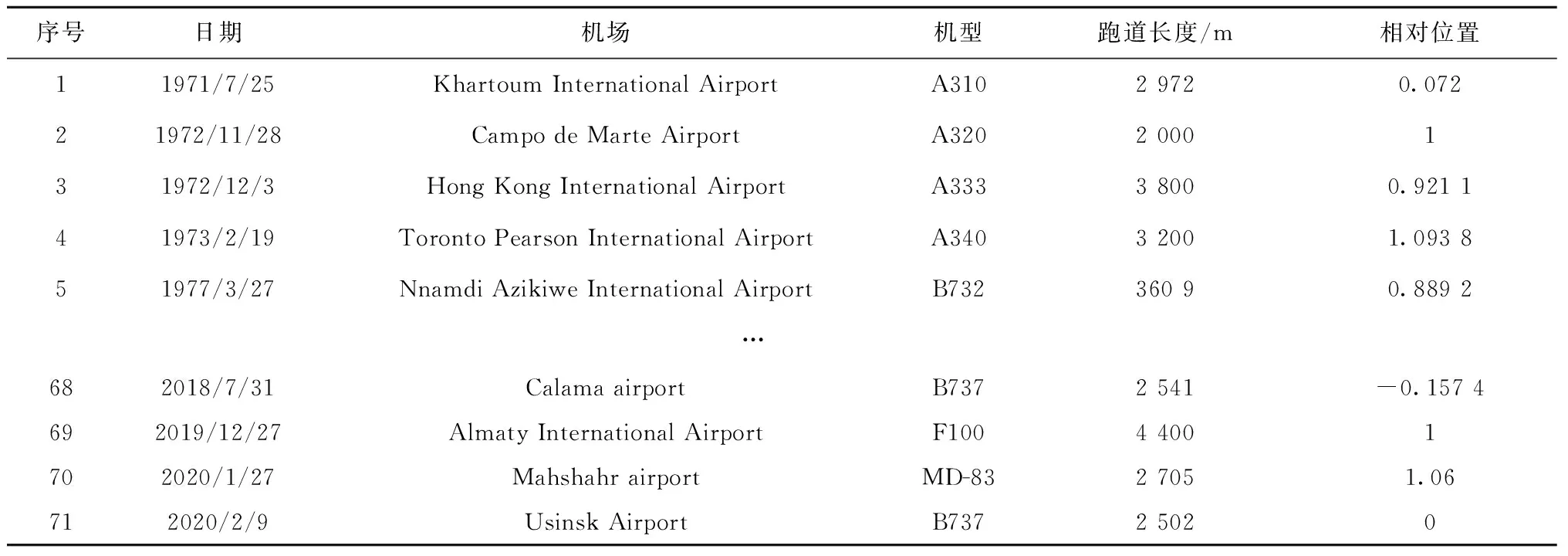
表2 部分跑道事故相对位置值

在表2中，若跑道事故的相对位置为k，当k>1时，表示事故发生在跑道末端延长线上；当k<0时，表示事故发生在跑道入口延长线上。本文将跑道分为间隔为0.1的10个等分区间，考虑到防吹坪、跑道端安全区、机场围界，跑道两端分别增加2个区间，进而将跑道及跑道延长线分为14个等分区间，则此时机场消防车所需保障的相对范围为[-0.2, 1.2]。通过统计事故在各等分区间内发生的数量及频率，得到跑道事故离散型概率分布函数g(S)，其值如表3所示。

表3 跑道事故离散型概率分布函数取值表

表中，区间[-0.2, -0.1]所对应的事故频率计算过程为：事故数/总有效事故数=10/71=0.140 845。由于频率的取值在[0.014 085, 0.197 183]之间，为合理构建机场消防站选址优化目标函数，对其进行规范化处理，公式如下：

(6)

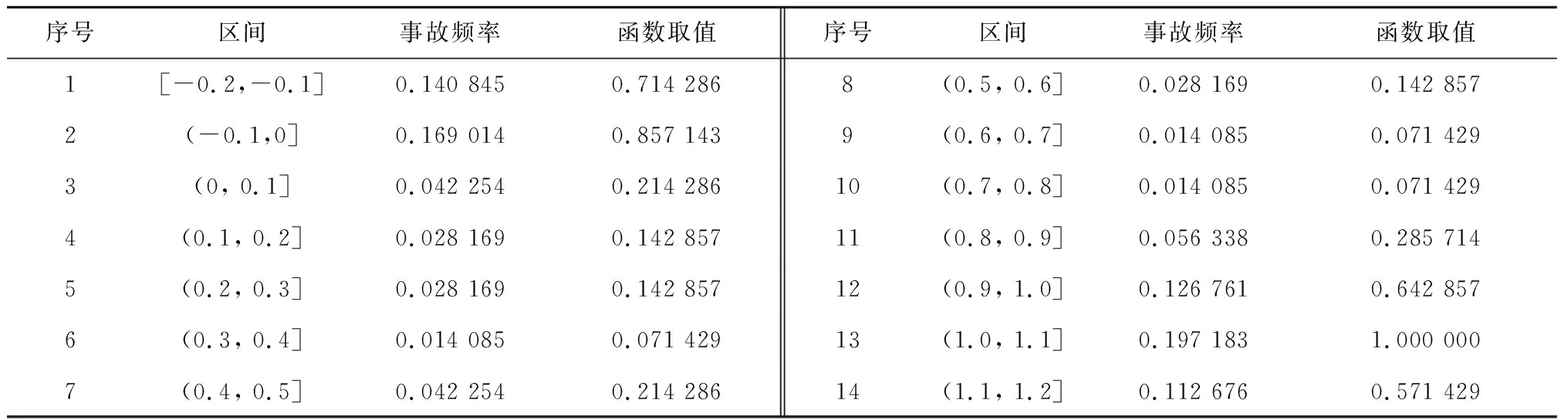
表4 规范化跑道事故离散型概率分布函数取值表

表中，区间[-0.2, -0.1]所对应的现有事故频率值计算过程为：原有事故频率/所有原有事故频率中的最大值=0.140 845/0.197 183=0.714 286。可以看出，跑道事故主要分布在跑道两端，跑道中部的事故概率相对较低。

4 机场消防站选址模型

(1)若Z≥6.043 km，即单个机场消防站无法满足2 min抵达跑道任意事故地点的需求。由于全球大多数机场的跑道及跑道附属区域在6.043 km以内，因此本文对这种情况不予讨论。

(2)若Z<6.043 km，即单个机场消防站能够满足2 min抵达跑道任意事故地点的需求。

在机场消防作业的实际情况中，其消防救援路线一般为以下两种情况[23]：

(1)飞行区共用道面 机场利用飞行区共用道面进行消防救援能够快速到达事发地点。但在机场消防车到达滑行道或跑道之前，不可避免会利用到机场服务车道，难以避免与机场车辆产生冲突，也有一定与航空器抢道的风险。

(2)飞行区专用道面 机场利用飞行区专用道面，即独立救援通道进行救援，能够有效避免与航空器以及机场场面内其他车辆产生冲突。其特点是快速有效到达事发地点，但增加了机场建设成本。根据机场消防救援路线的不同，本文作如下划分：

1)当机场消防救援路线为飞行区共用道面时，救援过程中的拥堵主要发生于机场消防车行驶到就近跑道或滑行道途中，即需考虑消防救援路线的拥挤程度。

2)当机场消防救援路线为飞行区专用道面时，因该道面只行驶机场消防车，即无需考虑消防救援路线的拥挤程度。

4.1 机场消防救援路线为飞行区专用道面

(1)模型的目标函数为：

(2)约束条件为：

机场消防车能够满足2 min行驶到需要保障范围的任意一点，即max{0, 1.2L-3.021 5}≤S≤min{L, 3.021 5-0.2L},其中L为跑道长度。

(3)目标函数取值都在[0, 1]内，无量纲差异，构建如下多目标规划模型：

s.t.

max{0,1.2L-3.021 5}≤S≤

min{L,3.021 5-0.2L},

0≤λ≤1。

(7)

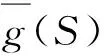
(8)

4.2 机场消防救援路线为飞行区共用道面

(1)模型的目标函数为：

2)消防救援路线拥堵程度尽可能小，即minh(S)；

(2)约束条件为：

机场消防车能够满足2 min行驶到需要保障范围的任意一点，即max{0,1.2L-3.021 5}≤S≤min{L,3.021 5-0.2L}，其中L为跑道长度。

(3)目标函数取值都在[0,1]内，无量纲差异，构建多目标规划模型：

s.t.

max{0,1.2L-3.021 5}≤S≤

min{L,3.021 5-0.2L}；

0≤x,y≤1；

x+y≤1。

(9)

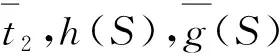
(10)

(11)

由于我国单跑道机场最大年旅客吞吐量不超过3 000万，单跑道机场最大年起降架次不超过20万，本文定义机场最大年旅客吞吐量为3 000万，机场最大年起降架次为20万。

5 案例分析

若未作特殊说明，本文以表1中的梯形隶属度函数描述消防救援路线拥堵程度，进行案例分析。

5.1 案例分析

某单跑道机场为4E级民用机场，跑道长度L=3.4 km，机场受海洋性季风影响，该机场跑道为南北方向，机场年旅客吞吐量为2 555.6万人次，年起降架次为18.6万架次。机场利用飞行区共用道面作为消防救援路线。在实际运行过程中，飞机一般为逆风起降：一是可缩短飞机起降的滑跑距离；二是可以获取更好的稳定性和安全性[23]。考虑飞机起降受风向影响，下面分两种情况进行讨论。

5.1.1 机场受南风影响

如图7所示，跑道端点分别为0 km、3.4 km，航站楼投影到跑道上的点分别为1.4 km、2.1 km。

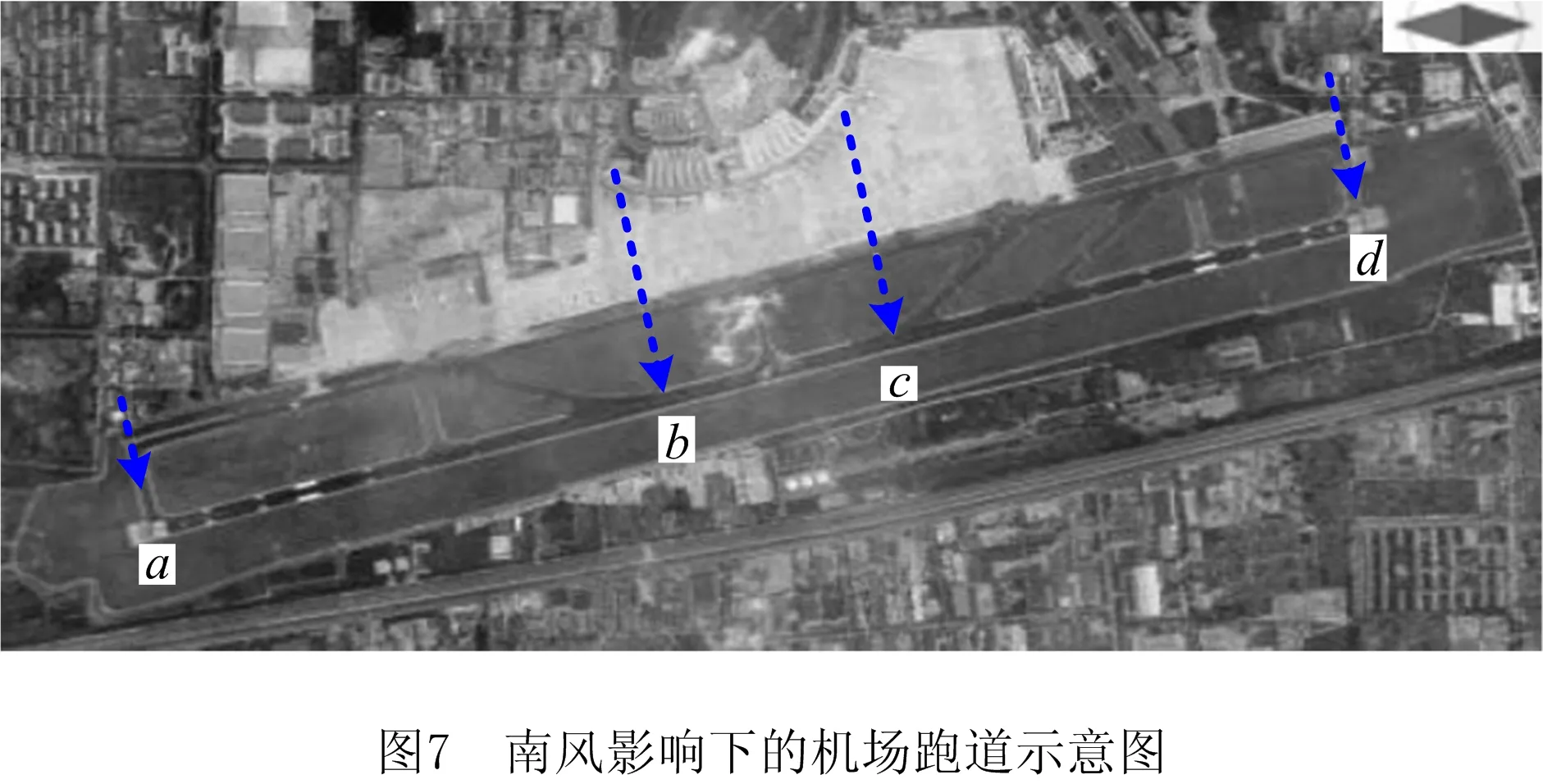
根据表1，梯形隶属度函数的参数值分别为a=0，b=1.4，c=2.1，d=3.4。由式(10)和式(11)可知：

将各点带入模型中：

s.t.

(12)

5.1.2 机场受北风影响

如图8所示，跑道端点分别为0 km、3.4 km，航站楼投影到跑道上的点分别为1.3 km、2.0 km。

根据表1，梯形隶属度函数的参数值分别为a=0，b=1.3，c=2.0，d=3.4。由5.1.1节可知，x=0.426，y=0.465。

将各点带入模型中：

s.t.

(13)

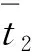
5.2 对比分析

将梯形隶属度函数、三角隶属度函数、高斯型隶属度函数、一般钟型隶属度函数带入模型中分别计算，进行对比分析。各函数参数值及计算结果如表5和表6所示。

5.2.1 参数说明

(1)表5中参数

1)梯形隶属度函数的参数值a，d为跑道端点，分别为0 km、3.4 km；b，c为航站楼投影到跑道上的点，分别为1.4 km、2.1 km。

2)三角形隶属度函数的参数值a，c为跑道端点，分别为0 km、3.4 km；b为航站楼中心投影到跑道上的点1.75 km。

表5 机场受南风影响隶属度函数参数及计算结果表

3)高斯型隶属度函数参数值μ为航站楼中心投影到跑道上的点1.75 km，σ表示拥挤程度分布。根据高斯型隶属度函数公式：

(14)

令S=0时，h(S)=0.000 1，即跑道端点的拥堵系数可忽略不计，进而σ=0.407 7。

表6 机场受北风影响隶属度函数参数及计算结果表

4)一般钟型隶属度函数参数值a为停机坪投影到跑道上的点0.45 km，c为航站楼中心投影到跑道上的点1.75 km，参数b表示函数值为1/2时所对应跑道投影位置。同理，根据一般钟型隶属度函数公式：

(15)

根据一般钟型隶属度函数参数定义，令h(S)=1/2时，S=b，即

(16)

解得b=1.3。

(2)表6中参数

1)梯形隶属度函数的参数值a，d为跑道端点，分别为0 km、3.4 km；b，c为航站楼投影到跑道上的点，分别为1.3 km、2.0 km。

2)三角形隶属度函数的参数值a，c为跑道端点，分别为0 km、3.4 km；b为航站楼中心投影到跑道上的点1.65 km。

3)高斯型隶属度函数参数值μ为航站楼中心投影到跑道上的点1.65 km，σ表示拥挤程度分布。根据高斯型隶属度函数公式：

(17)

令S=0时，h(S)=0.000 1，即跑道端点的拥堵系数可忽略不计，进而σ=0.384 4。

4)一般钟型隶属度函数参数值a为停机坪投影到跑道上的点0.7 km，c为航站楼中心投影到跑道上的点1.65 km，参数b表示函数值为1/2时所对应跑道投影位置。根据一般钟型隶属度函数公式：

(18)

根据一般钟型隶属度函数参数定义，令h(S)=1/2时，S=b，即

(19)

解得b=0.95。

5.2.2 结果分析

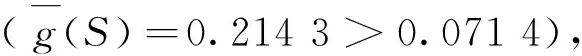
当机场受北风影响时(如表6)，在梯形隶属度函数、三角隶属度函数、高斯型隶属度函数下，机场消防站最优位置不在跑道中部，而是在从跑道北端延长线0.2L处开始，机场消防车2 min最远可行驶的理论位置，即X=L-S+0.2L=3.021 5；或从跑道南端延长线0.2L处开始，机场消防车2 min最远可行驶的理论位置，即X=S+0.2L=3.021 5。 在一般钟型隶属度函数下，机场消防站的最优位置仍在跑道中部。

由表5和表6还可以看出，高斯型隶属度函数和一般钟型隶属度函数下得到的结果受机场风向的影响较小。因而，相对本案例而言，上述两种隶属度函数所描述的机场跑道拥堵函数更具鲁棒性。特别地，一般钟型隶属度函数下，机场消防站的最优位置始终跑道中部，进而说明，当机场的拥堵主要集中在停机坪范围内时(如小型机场)，机场消防站应设置在跑道中部；反之，当机场的拥堵分散于整个跑道周围时(如大型机场)，机场消防站可能设置在非跑道中部。此外，机场风向会影响飞机的起降方向，但不影响该机场消防站的设置位置，例如，梯形隶属度函数下，受南风和北风影响的机场消防站最优位置均为南北方向跑道的1.059 km处。

5.3 灵敏度分析

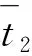
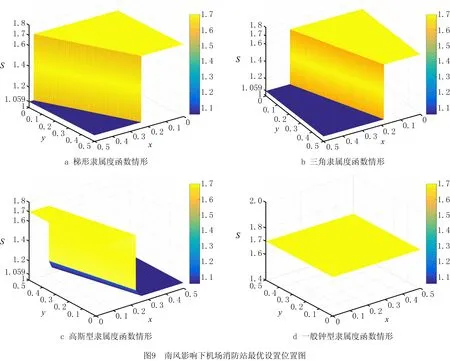
机场受北风影响时，对图10a～图10c而言，当x较小时，即机场年旅客吞吐量较小时，机场消防站设置在跑道中部；当x较大时，即机场年旅客吞吐量较大时，机场消防站最优位置不在跑道中部，而是在从跑道北端延长线0.2L处开始，机场消防车2 min最远可行驶的理论位置，即X=L-S+0.2L=3.021 5；或从跑道南端延长线0.2L处开始，机场消防车2 min最远可行驶的理论位置，即X=L-S+0.2L=3.021 5。 对于图10d而言，当x和y变化时，同理，机场消防站仍设置在跑道中部。

由图9c、图9d、图10c、图10d还可以看出，高斯型隶属度函数和一般钟型隶属度函数下得到的结果受机场风向的影响较小。因而，相对本案例而言，上述两种隶属度函数所刻画的机场跑道拥堵函数更具鲁棒性。此外，随着机场年旅客吞吐量x和机场年起降架次y的变化，机场消防站的最优选址位置可能发生变化，说明拥堵程度和事故分布可能影响机场消防站的选址，进而说明了在机场消防站选址优化问题中考虑救援路线拥堵程度和跑道事故分布等因素的合理性。

6 结束语

本文同时考虑了消防救援路线拥堵程度及跑道事故数据分布规律，结合相关规范要求，构建了机场消防站选址多目标规划模型，案例分析表明：

区别于既有规章建议，机场消防站的最佳位置不一定在跑道中部，与机场救援路线拥堵程度和跑道事故离散型概率分布息息相关；当机场航班量较小时，机场的拥堵主要集中在停机坪周围，此时将机场消防站设于跑道中部有利于快速抵达事故地点；当机场航班量较大时，机场的拥堵分散于整个跑道周围，机场消防站可能设置在非跑道中部；相较于本文所提的其他两类拥堵程度函数，高斯型隶属度函数和一般钟型隶属度函数所刻画的机场跑道拥堵函数更具鲁棒性。

未来将开展基于机场救援路线拥堵程度和跑道事故离散型概率分布的多跑道机场消防站选址优化模型研究，以及利用统计假设检验、回归分析等方法优化模型参数或直接确定拥堵程度函数实际决策模型。