基于气象相似日选取与提升回归树的光伏发电短期功率预测*

魏联滨 ，王 彬 ，王 莹 ，张海峰

(1.国网天津市电力公司，天津 300010；2.北京大学动力中心，北京 100871)

随着环境问题的日益突显、能源需求的不断增长以及光伏发电技术的逐步成熟，近年来光伏发电产业得到了快速发展。光伏发电输出功率具有强烈的随机性、波动性，随着光伏发电装机容量占比的不断提高，其输出功率的不确定性带来了一系列的调度运行问题。及时准确地预测光伏发电功率可以有效降低光伏发电给电网安全运行带来的不确定性。

通常情况下，光伏发电功率预测是以光伏电站历史运行数据和历史数值天气预报数据为基础，建立天气预报数据与光伏电站发电功率之间的映射关系，进而预测未来光伏电站的发电功率。文献[1]提出了基于极限学习机的光伏发电功率预测，但未根据气象条件选择训练数据集合。文献[2]提出了基于支持向量机模型的光伏短期功率预测，筛选历史气象相似日时未计算各种影响因素的权重。文献[3]提出了基于灰色神经网络组合算法的光伏发电功率预测，神经网络各种参数未优化，预测结果精度有待提高。文献[4]提出了基于深度学习的短期光伏发电预测方法，存在阴天天气情况下预测准确度不高问题。文献[5]建立了基于随机森林特征选择和CEEMD 的短期光伏发电预测，算法鲁棒性仍需提高。文献[6]提出了基于时变参数自适应离散灰色模型的光伏发电长期预测模型，该模型未考虑识别和修复原始数据中异常数据。本文提出基于气象相似日选取与提升回归树的光伏发电短期功率预测方法，通过动态时间弯曲距离选择与预测日气象因素相似的历史日集合作为训练样本集合，采用提升回归树构建光伏发电功率预测模型，提升了预测结果的准确性。

1 光伏发电功率影响因素

影响光伏发电功率的因素众多，主要包括气象因素和光伏发电组件。

1.1 气象因素

气象因素是影响光伏发电出力的主要因素，包括太阳辐照度、周围环境温湿度以及降雨降雪等天气过程。

太阳辐照度是指单位时间内垂直投射在单位地表面积上的辐照能量，值越大光伏电站发电功率越高。

环境温度是大气分子热运动的度量，温度越高光伏发电功率越大。环境湿度较大时，空气流动性差，阻挡了地表有效反射辐射，发电功率降低。

当光伏电站所处区域的天空云量增加时，云层的厚度、云底高度和云类的变化将导致大气折射、吸收、散射效应趋于复杂，会导致光伏发电功率发生随机性波动。

1.2 光伏组件条件

除了气象因素外，光伏组件的转换效率也是影响光伏发电功率的重要因素之一。光伏组件的转换效率主要受到逆变器性能、组件材质、安装角度、老化和遮挡等因素的影响。理论上，光伏发电功率预测需要全面考虑上述影响因素。但是逆变器性能、光电转换效率、组件安装角度等光伏电站本身属性在其投入运行时已经确定。对于某一个光伏电站，历史日发电功率数据和预测日发电功率对比，电站本身属性条件基本不变，不同之处主要是外在气象条件，电站本身属性条件可以转换为历史日发电功率数据。

2 气象相似日选择

影响光伏发电功率的气象条件包括周围环境温度湿度、降水量、太阳辐照度等。但是，各因素对光伏发电功率影响大小不同，需要确定各影响因素的权值，进而从历史数据找到与预测日气象条件最相似的历史日。

2.1 基于熵值法的气象因素权重计算

采用层析分析法计算各气象因素的权重系数，具体步骤如下:

(1)组织光伏业务专家明确各因素指标之间的相对重要性，参照判断矩阵标度表构建指标之间判断矩阵X＝(xij)n×n，标度表内容如表1 所示。

表1 判断矩阵标度表

(2)计算指标判断矩阵X的每一行元素的积Mi

(3)计算每一行Mi的n次方根值:

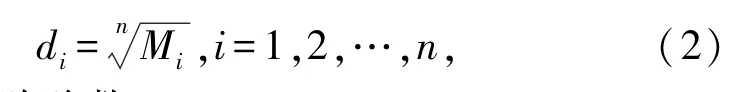
式中:n为矩阵阶数。

(4)计算一级指标权重系数:

与层析分析法相比，熵值法完全基于数据分布情况计算各指标的权重系数，避免了人为因素的影响。采用熵值法计算影响光伏发电气象各因素的权重系数，具体步骤如下:

(1)指标数据标准化。由于气象各因素的量纲、数量级差异较大，需要对各指标数据归一化至指定区间，具体公式如下:

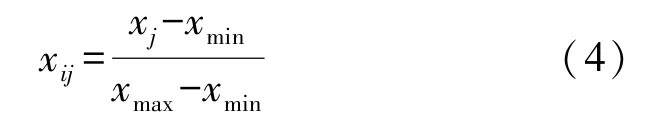
式中:xj为第j项因素值，xmax为气象数据集合中第j项因素最大值，xmin为气象数据集合中第j项因素最小值，xij为第i个气象日第j项因素标准化处理后的值。

(2)计算指标比重矩阵。根据步骤1 结果计算第j项因素下第i个时间点的比重yij，具体公式如下:

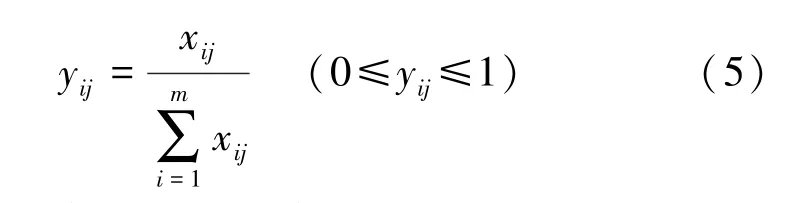
(3)计算信息熵值和信息效用值d。根据步骤2 结果可以计算第j项因素的信息熵值ej，具体公式如下:

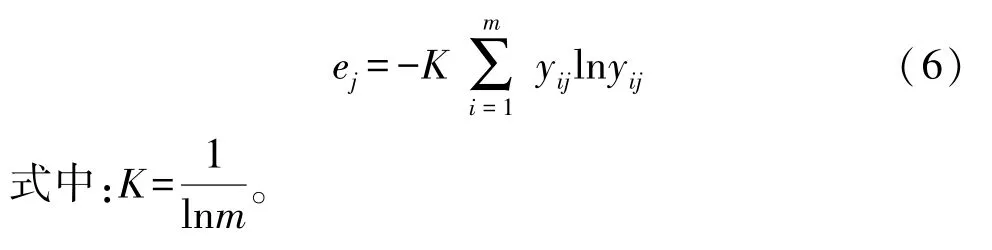
接着，计算第j项指标的信息效用价值dj，具体公式如下:

(4)计算各指标因素权重。具体公式如下:

熵值法是指经过对实际样本集合进行整理、计算、分析，从而得到权重系数。该方法避免了人为因素的影响，比较符合实际的数据分布。本文采用熵值法确定气象各因素指标权重系数。

2.2 基于DTW 的气象因素相似度计算

气压、温度、相对湿度、降水量、太阳辐照度等气象数据是典型的时间序列数据。动态时间弯曲(dynamic time warping，DTW)是一种有效的时间序列对象相似性度量方法。它通过调整时间序列不同时间点对应元素之间的关系来获取一条最优弯曲路径，使其能很好地度量时间序列之间的相似性。假设有两条时间序列A＝{a1，…，ai，…，am}和B＝{b1，…，bj，…，bn}，m和n分别表示时间序列A和B的长度，首先构造一个m×n的矩阵M，元素M(i，j)为ai与bj之间的距离，然后在矩阵中寻找一条使两条序列间累积距离最小的弯曲路径。弯曲路径W＝{w1，…wk，…，wK}是矩阵M一组连续的元素集合，并且满足以下约束:

(1)有界约束:max(m，n)≤K≤m＋n－1。

(2)边界约束:元素w1＝M(1，1)和wK＝M(m，n)分别是弯曲路径的起点和终点。

(3)连续性约束:给定元素wk＝M(i，j)，其相邻元素wk－1＝M(i′，j′)需满足i－i′≤1，j－j′≤1，即弯曲路径元素是相邻的。

(4)单调性约束:给定元素wk＝M(i，j)，其相邻元素wk－1＝M(i′，j′)需满足，i－i′≥0，j－j′≥0。

矩阵T＝{(x1，y1)，(x2，y2)，…，(xN，yN)}中存在多条满足上述约束条件的弯曲路径，但是时间序列A和B的DTW 距离是最小的弯曲路径。弯曲路径是一种利用动态规划算法求解的最优化问题，其最优解子结构为:

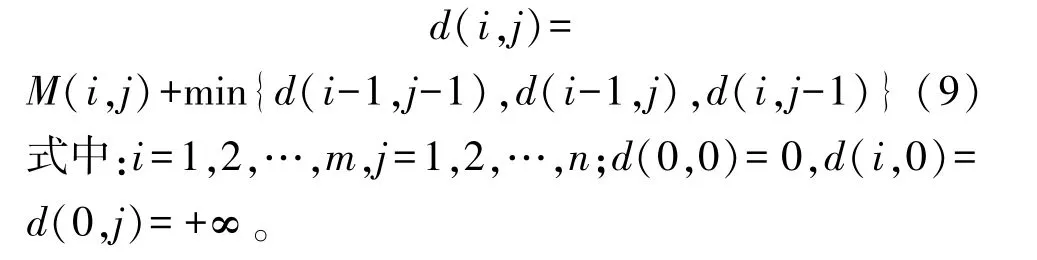
因此，上述时间序列A＝{a1，…，ai，…，am}和B＝{b1，…，bj，…，bn}的DTW 距离为Ddtw(A，B)＝d(m，n)。相比于常用的欧氏距离，DTW 能更准确完整地反映两个序列之间的相似程度。

从历史数据搜索预测日气象条件最相似的历史日的步骤如下:

(1)根据历史日各气象因素数据，采用熵值法计算各因素的权重w。

(2)对于预测日，计算每个历史日每个气象因子与预测日相应因子的DTW。

(3)计算每个历史日与预测日气象因子的相似度。

(4)从历史日集合选择与预测日气象因素最相似的历史日子集。

3 梯度提升树

提升方法是一种典型的集成学习方法。在分类或回归问题中，它通过改变训练样本的权重，构建多个分类(回归)模型，并将这些基本模型线性组合提高分类(回归)的性能。提升回归树是以回归树为基本模型的提升方法。

3.1 回归树

假设X与Y分别为输入和输出变量，并且Y为连续变量，给定训练数据集D，D＝{(x1，y1)，(x2，y2)，…，(xn，yn)}，考虑如何生成回归树。

如果一个回归树有M个叶子，那么该回归树将输入空间X划分为M个单元，每个单元Xm有一个输出值cm。回归树模型可表示为:

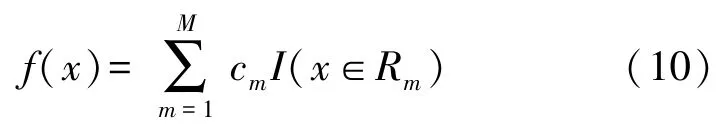
式中:I(x∈Rm)为示性函数，当x∈Rm时取值为1，否则取值为0。

当输入空间的划分确定时使平方误差最小，单元Rm输出值cm的最优值则是Rm上的所有输入实例对应的输出yi的均值，即

如何对输入空间进行划分。采用启发式思想回归树具体生成算法如下:

3.2 梯度提升算法

提升回归树模型采用加法模型和前向分步算法实现学习的迭代优化，具体表示为:

式中:T(x；Θm)表示回归树，Θm为回归树参数，M为回归树数量。

采用前向分布算法，首先确定初始提升树f0(x)＝0，第m步模型为:

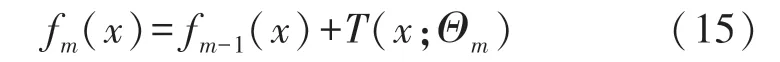
式中:fm－1(x)为当前模型。

在提升回归树生成过程中，需要经验风险最小化确定下一棵回归树的参数Θm，当采用平方差作为损失函数时则转化为求解:

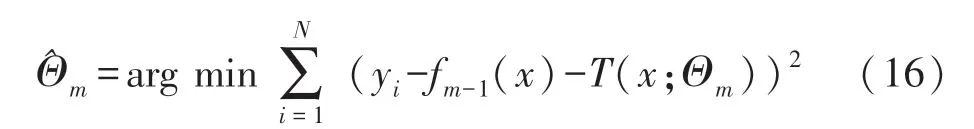
式中:yi－fm－1(x)为当前模型拟合样本数据的残差。因此在提升回归树构建过程中只需要拟合当前模型的残差[13－15]。提升回归树生成算法如下:

4 应用分析

以某地区2020 年1 月至3 月的数值天气数据和2 kW 室外自动跟踪光伏电站发电量实测数据作为样本数据集合，对本文提出的基于气象相似日选取与提升回归树的光伏发电功率预测模型进行了验证，并对预测结果的精确性进行分析。数据集包括每15 min 温度、相对湿度、风速、太阳辐照强度、光伏电站并网功率。

4.1 气象相似日选取

首先，提取历史气象数据，气象数据具体内容如表2 和图1 所示:

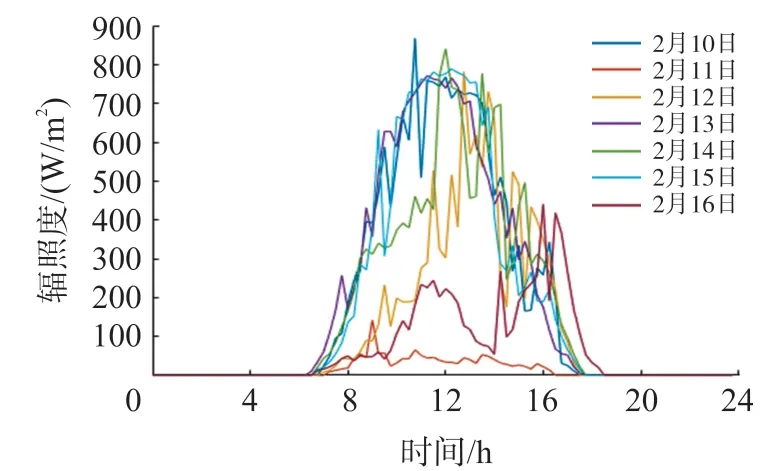
图1 历史日辐照度曲线

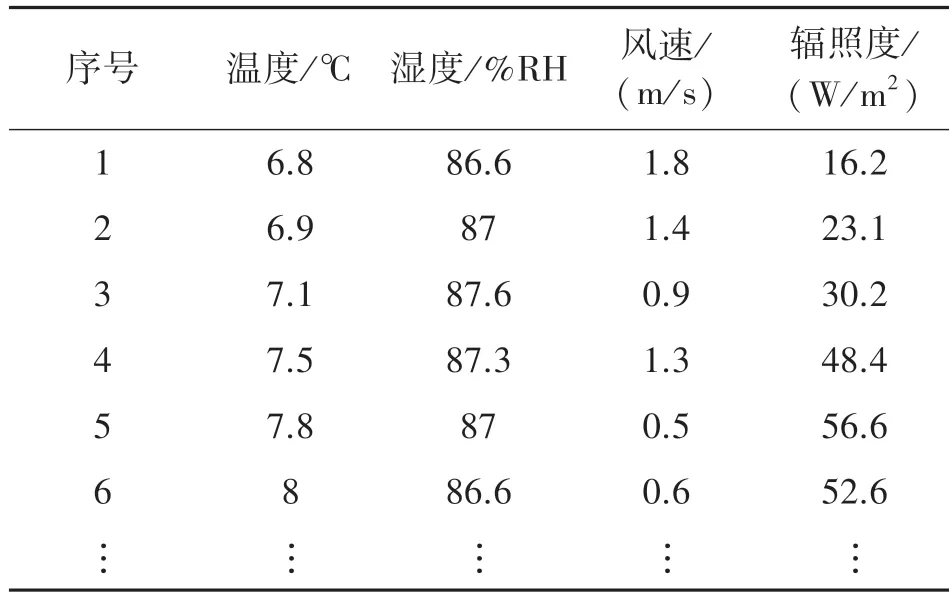
表2 气象数据

接着，应用熵值法计算各个气象影响因素的权重，经过计算温度、湿度、风速、太阳辐照强度的权重分别为0.063、0.040，0.104、0.793。

然后，计算历史日气象因素数据之间的DTW，太阳辐照度曲线如图1 所示，它们之间的DTW 矩阵如表3 所示:

表3 辐照度序列之间DTW

可以看出，辐照度曲线越接近，其DTW 越小。

最后，计算各因素之间DTW。然后乘以它们之间权重就是气象相似度大小。对于3 月20 日，其相似日如表4 所示:

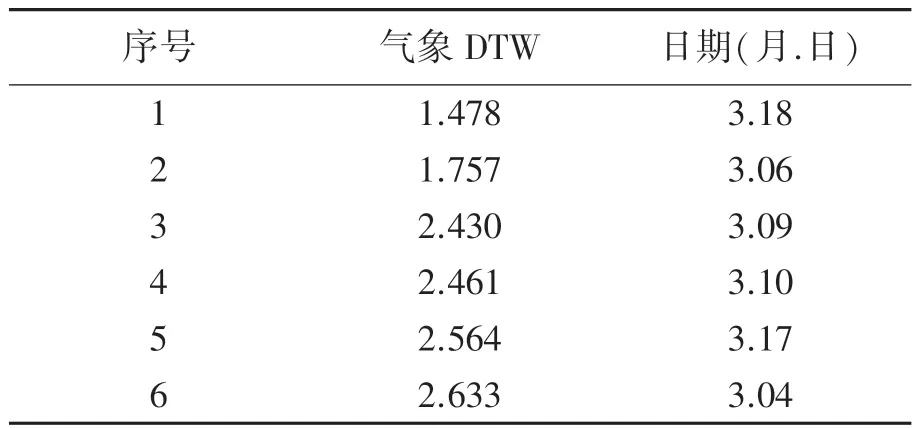
表4 历史气象相似日

历史相似日和预测日并网功率如图2 所示，对比分析3 月18 日、3 月6 日和3 月9 日与3 月20 日并网功率数据，从图可以看出气象条件越相似该历史日和预测日的光伏发电短期功率曲线越吻合。

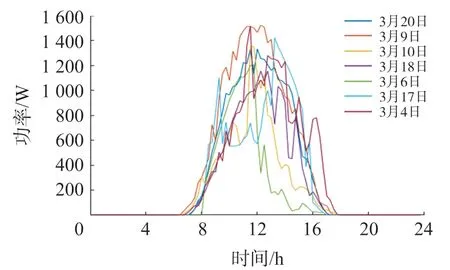
图2 历史日发电功率曲线

4.2 结果分析

对于每个预测日的光伏发电功率预测，将k个历史相似日的温度、相对湿度、风速、太阳辐照时间序列数据，以及每个历史相似日前一天发电功率时间序列数据作为模型输入变量，将k个历史相似日发电功率数据作为模型的输出变量，构建光伏发电功率预测模型。

为进一步分析本文模型的正确性与精确性，将回归树模型、气象相似日－回归树模型、提升回归树模型预测结果与本文所提出的相似日－提升回归树模型的预测结果从均方误差(MSE)、均方根误差(RMSE)、平均绝对误差(MAE)、拟合度(RSquared)四个方面进行对比分析，结果如表5 所示。

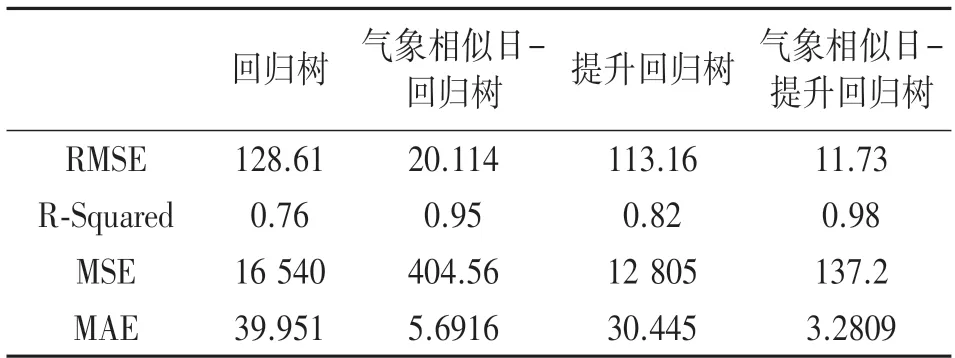
表5 预测结果对比分析

可以看出，气象相似日－提升回归树较回归树、提升回归树的拟合度(R-Squared)提升，均方误差(MSE)、均方根误差(RMSE) 和平均绝对误差(MAE)降低，因此相比其他方法，气象相似日－提升回归树误差减小的同时预测准确性度显著提高。

5 结论

光伏发电功率受气象因素影响随机波动性较大，随着并网容量日益增大，对电网的安全运行影响越来越大。本文提出基于气象相似日选取与提升回归树的光伏发电功率预测方法，通过动态时间弯曲距离选取与预测日相关度高的历史样本作为训练样本，采用集成学习方法对光伏发电功率进行日前预测。验证结果表明，本文提出的气象相似日选取与提升回归树的预测模型具有较高的预测准确度，可以有效降低光伏发电给电网安全运行带来的不确定性。