考虑动态耦合作用的高铁站周边路网风险辨识

徐 标，崔 欣，秦 汉，胡 渊，张鸿鸣

（1.长安大学电子与控制工程学院，陕西 西安 710064；2.长沙市规划设计院有限责任公司，湖南 长沙 410000；3.中铁第四勘察设计院集团有限公司，湖北 武汉 430063）

0 引言

随着我国城市化进程的加快，各大城市热点区域的交通需求正在不断增大。高铁站作为典型的城市化产物，其安全的运行对推动城市经济发展、方便群众出行、提高运输效率、构建综合交通运输体系有着重要意义。在与城市道路交通网络融合发展的过程中，由于高铁站周边路网客流量大、部分进出站道路设计不合理等原因，部分高铁站周边路网存在单点或单线客流集散不均衡的状况，从而导致车辆拥堵等现象频发[1]，严重影响了路网的通行效率和乘客的正常出行。因此有必要对高铁站周边路网的风险进行评估，分析不同时空下路网风险的变化规律，进而识别出具有较高风险的交叉口和路段，对其进行重点管控，保障高铁站周边路网交通的稳定、高效运行。

风险是指事故发生的概率及其对系统性能的影响的组合。由于交通事件的发生具有随机性，往往无法准确判断其发生概率，因此大多数学者主要分析网络单元失效后造成的影响。目前对交通路网风险的研究方法主要分为两类。一类方法是基于复杂网络理论，从拓扑结构去分析交通网络风险，如Liu 等人[2]通过构建L 空间加权交通网络，提出一种复杂度较低的介数中心性近似算法来识别网络中的关键节点；张树德[3]基于复杂加权网络对网络的物理结构进行抽象，利用层次分析法计算不同拓扑指标的权重，以此识别重要节点和路段。另一类方法主要从交通网络功能特性的角度进行研究，如刘梦月等人[4]综合交通需求和交通供给构建了不同维度下灾后路网可靠性模型，用于辨识网络风险；李君羡等人[5]基于蒙特卡洛模拟的思想，考虑路段行程时间序列相关性来辨识网络风险。

相比之下，从网络拓扑结构或功能特性单一角度分析网络风险无法准确衡量路网的实际运行风险，因此许多学者综合考虑网络的拓扑特性和交通功能特性进行研究。如López 等人[6]结合网络拓扑和流量分布，对不同的网络配置和空间自相关水平进行数值模拟，分析网络单元失效对网络脆弱性的影响，以此来确定网络单元的重要性。Nogal 等人[7]基于路网平均出行时间和流量构建网络可靠性和可达性等指标来量化网络风险。杜丽衡[8]根据路网拓扑特征和功能特征，基于正向评价和逆向假设的思想提出AHP-Entropy-TOPSIS方法来辨识路网的风险节点和路段，并根据风险系数划分了不同的层级。张勇等人[9]从路网整体风险的角度，基于道路车辆排队容量和截面通行能力的约束构建路网交通流模型，分析各路段依次失效对网络鲁棒性的影响，以此来评估网络风险。

然而，以上研究主要基于网络拓扑结构和功能特征来构建系统风险评估指标，对于网络连通性较强、客流集散需求高的高铁站周边路网并不适用。该类路网的网络单元耦合作用强，在受到大客流冲击时会面临更高的运行风险。因此，本文将在网络拓扑结构和功能特征的基础上，考虑网络单元的耦合作用构建风险评估模型，并以西安北站周边路网为例，对不同需求下网络风险的动态变化进行分析。

1 高铁站周边路网风险辨识模型构建

相比于城市中位于其他区域的道路网络，高铁站周边路网具有车流量与客流量大、集疏散需求高等特点，因此密度更高，不同交叉口、不同路段之间的耦合作用显著。故本文在构建的高铁站周边路网风险辨识模型时，不仅考虑道路网络中不同交叉口和路段的拓扑特性、功能特性，还重点考虑不同交叉口和路段之间的耦合作用，以期更加准确地识别路网中具有高风险的交叉口和路段。本文所提出的高铁站周边路网风险辨识模型如图1所示。

图1 高铁站周边路网风险辨识模型

1.1 交通网络性能评估指标

基于图论和复杂网络理论，将高铁站周边路网中的交叉口抽象为网络图中的节点，将交叉口之间的路段抽象为网络图中的边，即可构建由节点集合和边集合组成的交通网络。在现有研究中，衡量交通网络中节点和边性能的常用指标包括度[10]、介数[11]、离心率[12]、负载系数和饱和度[13]等，大致可分为拓扑类和功能类两种。

1.1.1 衡量网络节点和边性能的拓扑指标

对于网络中的节点而言，节点的度Di是指网络中与该节点直接相连节点的数量，可用于衡量节点在网络中的重要程度，其计算公式见式（1）；介数φi是指网络中经过该节点的OD 数占网络所有OD 数的比例，可以反映该节点在网络中的作用和影响力，其计算公式见式（2）；离心率ui是指该节点与网络中其他节点最大距离的倒数，其是衡量节点网络中心性的常用指标，计算公式见式（3）。

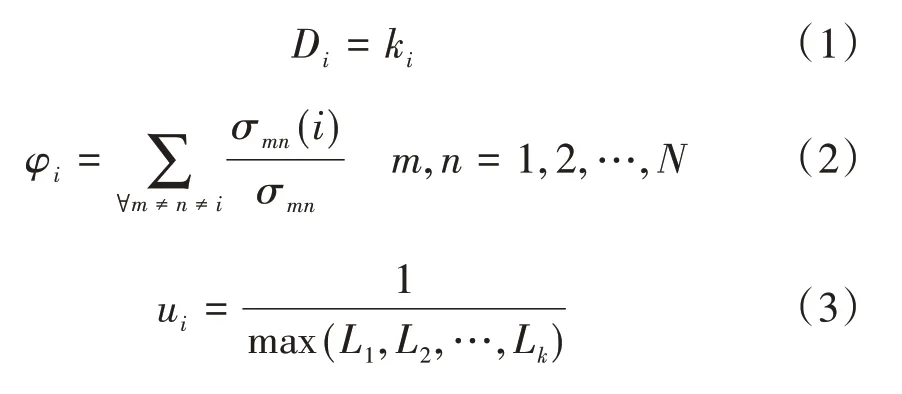
式（1）～式（3）中：ki为与节点i直接相连的节点数量；m和n为网络中任意不为i的节点；N为网络中的节点总数；σmn(i)为m和n之间经过节点i的最短路径数；σmn为m和n之间的最短路径数；Lk为节点i到节点k的最短路径长度（m）。

对于交通网络中的路段而言，路段a里程占比∂a是路段长度的量化指标，可用来衡量路段对交通的承载能力，计算公式见式（4）；路段介数φa表示网络OD间通过路段a的最短路径占比，也是路段重要性评价常用的指标，计算公式见式（5）。

式（4）～式（5）中：La为路段a的长度（m）；L为路网中路段总里程（m）；u和v为网络中任意不为a的路段；M为网络中除路段a外的其他路段数；σuv(a)为u和v之间经过a的最短路径数；σuv为u和v之间的最短路径数。

1.1.2 衡量网络节点和边性能的功能指标

交叉口的交通运行状态常用交通负载系数来衡量[14]，该系数的大小取决于交叉口相邻路段的交通状态。路段的功能特性可通过路段饱和度和路段阻抗来分析。其中，饱和度Ma(t)是指路段交通量和通行能力的比值，它表示路段在某一时间段内的拥挤状况，计算公式见式（6）；路段阻抗是指路段行程时间，可以反映车辆在道路上通行的难易程度，计算公式见式（7）。

式（6）～式（7）中：Qa(t)为路段a在t时段内的流量（pcu/min）；Ca表示路段a的通行能力（pcu/min）；为路段a自由流下的行程时间（s）；α和β为阻抗参数，参照美国公路局标准，α取0.15，β取4。

1.2 不同网络单元之间的耦合性

相比于城市中的一般路网，高铁站周边路网中不同交叉口以及不同路段之间的耦合作用显著。因此在构建高铁站周边路网风险辨识模型时，需将耦合性纳入考量。

1.2.1 网络中不同节点之间的耦合作用

当高铁站周边路网某一交叉口因交通事故导致车辆无法正常通行时，该交叉口处的交通负载会通过交通网络转移到其他路段和交叉口（相邻节点），从而对网络中其他节点处的交通状况产生影响。此外，交通流的传播需要一定时间，因此节点间的距离阻抗决定影响程度。综上可得出不同节点之间的耦合关系，如式（8）所示。

式（8）中：ηi为节点i和其相邻节点间的耦合系数；dij为节点i和节点j间的距离（m）；λj为相邻节点j的交通负载系数；ni为与i节点相邻的节点数。

1.2.2 网络中不同边之间的耦合作用

高铁站周边路网中的路段是通过交叉口连接的，当高铁站周边路网中某条路段发生拥堵时，路段上交通流的转移通过路段两端的交叉口传递到其他路段，因此道路两端交叉口的拥堵或畅通将直接决定路段间耦合关系的强弱。所以，在分析网络中不同边之间的耦合作用时，有必要对实际路网中不同路段两端交叉口的交通状态进行分析。将交叉口的平均交通负载系数作为区分节点畅通和拥堵的边界条件。

当交通负载系数小于等于平均交通负载系数时，认为节点处于畅通状态，如式（9）所示。

式（9）中：λi为节点i的交通负载系数；N为网络中的节点总数；λj为网络中任一节点j的交通负载系数。

当路段两端的交叉口处于畅通路况下，节点流量的流入与流出受到的阻碍较小，即近似认为其处于自由流下的平衡状态，此时更多考虑交叉口的拓扑特性对路段的影响。交叉口的拓扑系数ri计算公式见式（10）。

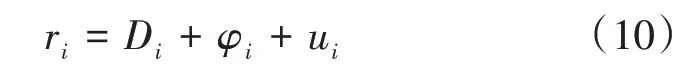
式（10）中：Di为节点i的度；φi为节点i的介数；ui为节点i的离心率。

若网络中节点（交叉口）的交通负载系数大于平均交通负载系数，则认为其处于拥堵状况，如式（11）所示。

拥堵情况下交叉口处于交通饱和态，交叉口的交通流量要不断往外转移以缓解拥堵（转移示意见图2）。当流入的流量相对较少时，为简化计算可以忽略流入交叉口的流量。

图2 交通流量转移示意图

从用户路径选择的角度综合分析流量转移，基于出行时间最短来构建流量转移关系式，因此路段的介数和饱和度共同决定着节点流量转移的概率。最终根据式（5）路段介数和式（6）路段饱和度倒数的乘积得出节点流量转移概率计算公式：

式（12）中：pia(t)为节点i流量在t时段内转移至路段a的概率；φa为路段a的介数；Ca为路段a的通行能力（pcu/min）；Qa(t)为路段a在t时段内的流量（pcu/min）；其余变量含义同前。

根据流量转移概率和交叉口的交通流量，可计算出节点i转移至相连路段a上的交通流量qia：

式（13）中：Qi(t)为节点i在t时段内的流量（pcu/min）。

在交通流量转移的过程中，路段阻抗会增大，因此交叉口和路段之间的功能耦合可通过交通流量转移前后路段阻抗的变化率来度量。根据式（7）可计算出拥堵节点流量转移后的路段阻抗：

式（14）中：为拥堵节点流量转移后路段a的阻抗（s）。

根据拥堵节点流量转移前后的路段阻抗，可以得到路段a的阻抗变化率wia(t)，即节点i和路段a间的功能耦合，计算公式见式（15）。

对于每条路段而言，路段两侧的拥堵交叉口和路段均存在功能上的耦合，如图3所示。

图3 路段端点流量转移示意图

路段两端的交叉口共有3 种不同的状态。若两个端点均处于畅通状态，只考虑端点自身的拓扑结构对路段的影响，结合式（10）端点拓扑系数，可将路段端点拓扑系数在路网中的占比作为耦合系数，计算公式见式（16）；若畅通节点和拥堵节点同时存在，在构建耦合系数时，除拓扑系数外，还应考虑路段和拥堵节点的功能耦合，因此结合式（15）的功能耦合关系，可得到节点和路段的耦合系数，计算公式见式（17）；若两个端点都处于拥堵状态，则需同时考虑端点的拓扑系数以及路段与端点间的功能耦合，计算公式见式（18）。

式（16）～式（18）中：Ra为路段a的耦合系数；ri和rj为路段a端点i和端点j的拓扑系数；wia(t)和wja(t)为路段a和端点i、端点j的功能耦合系数；n为网络中的节点数；rm为网络中任意路段端点m的拓扑系数。

1.3 高铁站周边路网风险辨识方法

1.3.1 网络单元的风险评估方法

对于网络中的节点，其风险评估方法如式（19）所示。式（19）中：Zi为节点i的风险系数；w1,w2,w3,w4,w5分别为各节点风险评价指标的权重；其他参数含义同前。

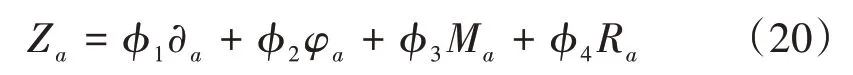
对于网络中的边，其风险评估方法如式（20）所示。式（20）中：Za为路段a的风险系数；ϕ1,ϕ2,ϕ3,ϕ4分别为各路段风险评价指标的权重；其他参数含义同前。

由于以上指标量纲不同，因此在计算时需将各指标的数据进行归一化处理，然后基于因子分析法计算相应的权重[15]。

1.3.2 网络风险评估模型

在实际的交通网络中，网络单元失效会直接造成用户的平均出行时间损失。因此，可基于节点和路段失效后用户平均出行时间变化率来衡量交通网络风险。网络风险通过节点和路段的风险程度进行度量，如式（21）～式（22）所示。

2 实例分析

2.1 西安北站周边路网建模

基于高铁站前区域功能布局的“三圈层”理论[16]，本文选取西安北站高铁枢纽周边路网，其包括元朔路、朱宏路、元凤二路、建元路、凤城九路、未央路等多条主干道路。基于TransCAD构建路网图（见图4），共包含35 个交叉口和52条路段，图中的数字对应着路段和交叉口的编号。

图4 西安北站周边路网图

由图4 可看出，西安北站周边路网交通布局以主干路和次干路为主、快速路和支路为辅，形成了一个局部的方格网。本文所需要的拓扑数据包括节点度、介数、离心率、路段长度，借助Gephi、MATLAB 以及百度地图测距工具进行统计；交通流数据包括节点负载、路段流量、路段通行能力，通过调查实际交通状况获取。考虑到度、介数、交通负载系数等拓扑和功能指标在评估交通网络风险时存在明显差异[6]，为避免指标间的多重共线性，本文采用斯皮尔曼相关系数分析节点和路段风险评价指标之间的相关性，相关系数矩阵见图5。由图5可看出，各指标间线性相关性较低，彼此独立。

图5 风险评估指标之间的相关系数矩阵

2.2 网络风险评估

根据式（19）和式（20）可计算出每个节点和每条路段的风险系数，然后将结果进行归一化处理。由于风险评估模型中的功能指标会随着网络中交通需求的变化而动态变化，因此本文是基于动态交通需求下的风险评估。首先根据低峰时段的路段流量，基于TransCAD 的OD 反推[17]得到初始状态下的OD 需求，将其定义为低需求；然后在此基础上分别将需求增大到初始状态的3 倍和5 倍来模拟不同的交通需求，最后根据不同需求绘制节点和路段的风险分布图（见图6）。由图6 可看出，随着交通需求的增加，距高铁站1km范围内的交叉口8、交叉口12、交叉口13 以及路段7、路段18、路段21的风险明显增加。

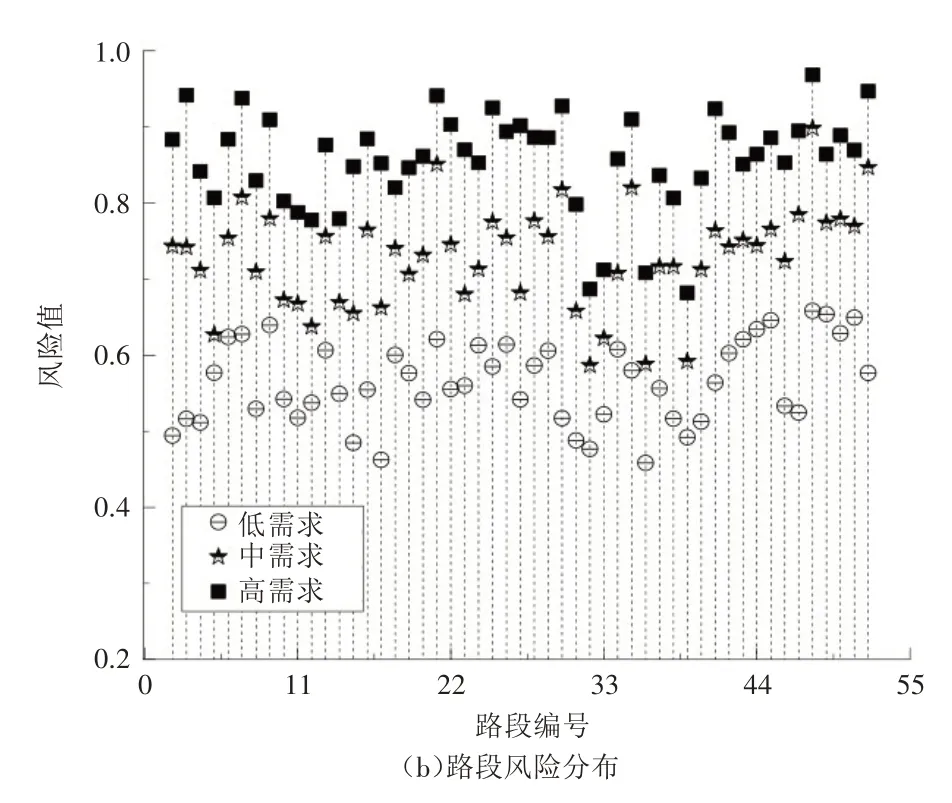
图6 风险值分布图

当需求增大到初始状态的3 倍和5 倍后，不同节点的风险变化率如表1 所示。由表1 可看出，当路网交通需求增大到初始状态的3 倍后，节点20（明光路—凤城十一路交叉口）的风险变化率达到了20%；当路网交通需求增大到初始状态的5倍后，节点1（元凤二路—朱宏路交叉口）的风险显著增加，达到了36.44%，因此该方法可有效识别不同交通需求下路网的风险源。

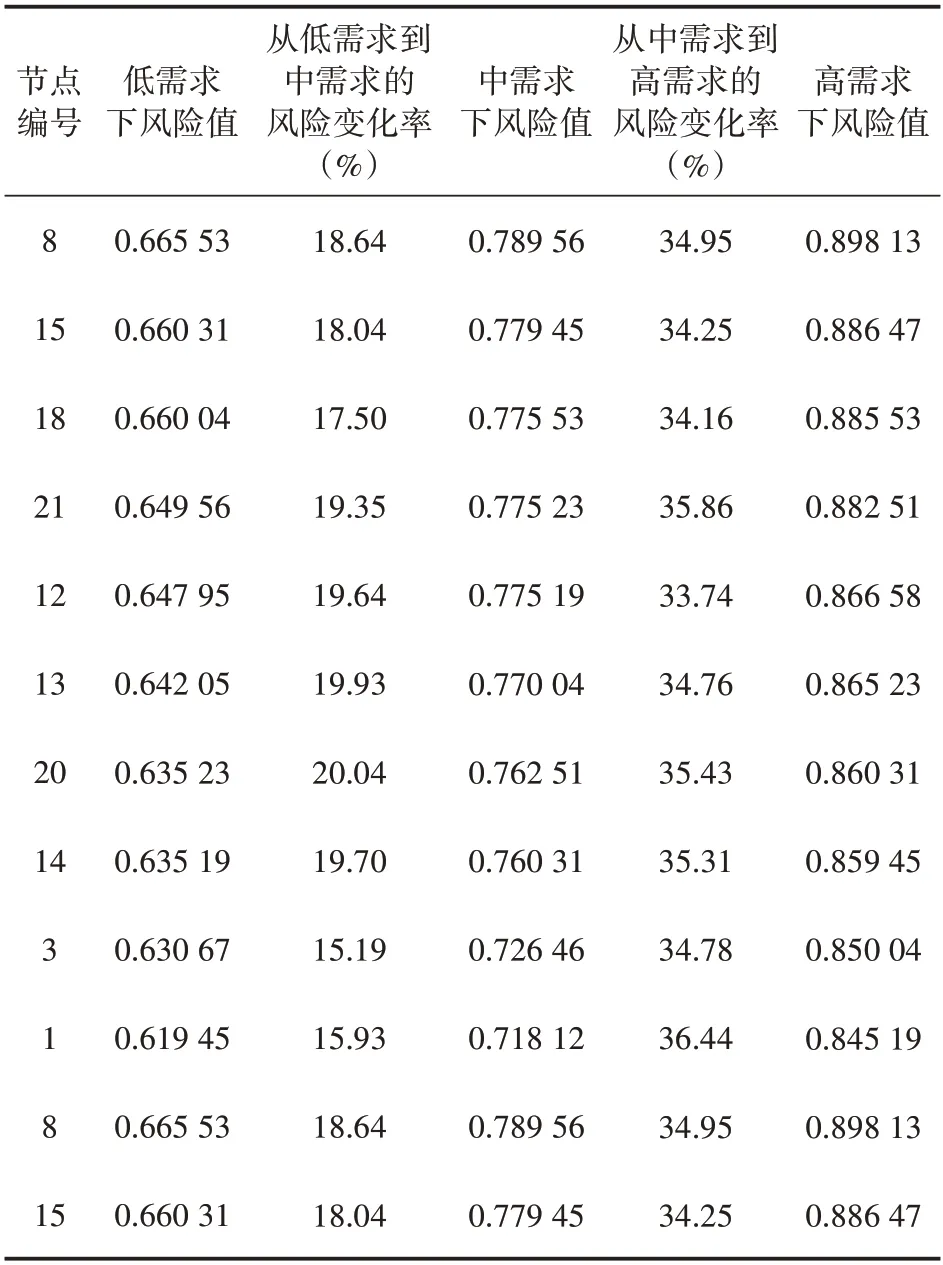
表1 不同需求下节点风险值及其风险变化率

当交通需求增大到初始状态的3 倍和5 倍后，不同路段的风险变化率如表2 所示。由表2 可看出，当路网交通需求增加到初始状态的3 倍后，路段45（凤城十路西侧）和路段50（凤城十路西侧）的风险变化率达到了20%。当交通需求增大到初始状态的5 倍时，路段18（凤城十二路）的风险显著增加，风险变化率达到了42.06%。

表2 不同需求下路段风险值及其风险变化率

为明确节点和路段对路网风险的影响，根据式（21）～式（22），可计算风险较高的节点和路段失效后路网风险值和网络用户平均行程时间损失，如表3所示。

表3 不同节点和路段对路网风险的影响

由表3可看出，风险最高的节点8（朱宏路—元朔路交叉口）失效后导致路网用户平均出行时间损失高达2.7h，路段48（朱宏路南侧）失效后导致路网用户平均出行时间损失高达1.6h。节点对路网风险的影响要大于路段，这是因为节点连接了较多的路段，一旦失效可能造成多条路径无法正常通行。

2.3 评估模型的对比与验证

根据Welch 等人[18]的研究，节点和路段的风险可基于韧性评估，该研究用与节点相连路段的容量、车速、距离和节点间影响系数的乘积来计算韧性。为验证本文构建的风险辨识模型的有效性，选取西安北站周边路网中主干路的10 条路段，在不同交通需求下计算每条路段的风险值并排序，排序结果如表4所示。

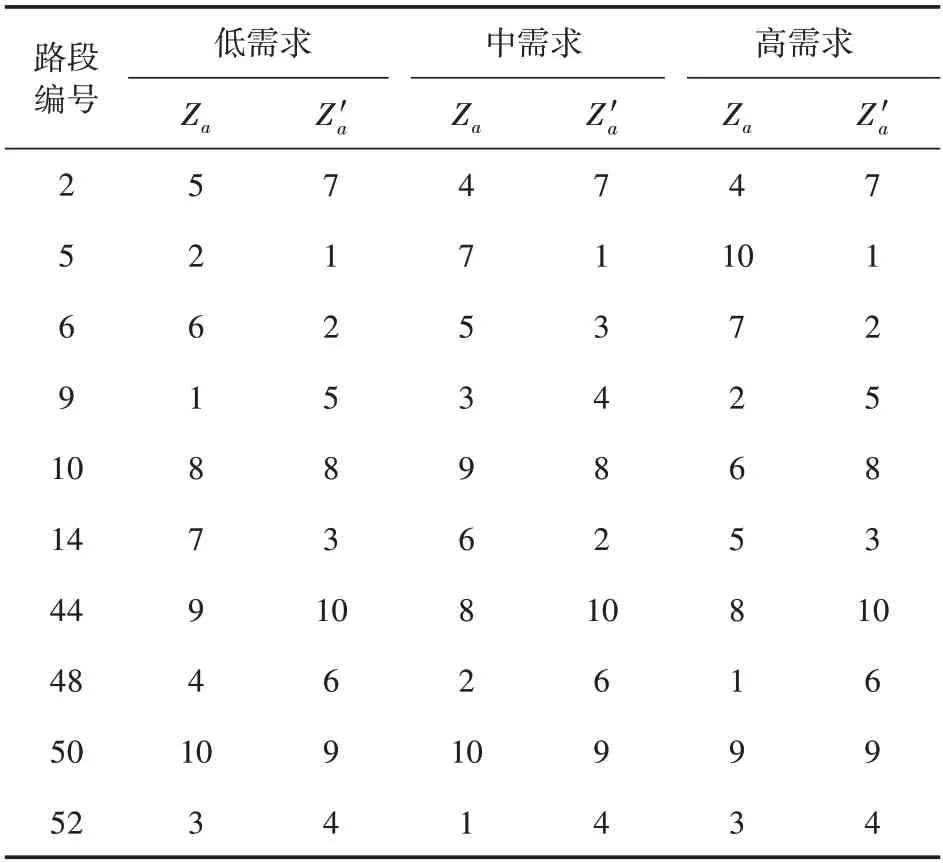
表4 不同需求下路段风险排序

表4 中Za和Za′分别表示本文所提出的风险评估指标和Welch 模型的风险评估指标。根据表6 中不同需求下路段风险评估结果，可以看出未考虑网络单元拓扑和功能耦合的Welch 风险模型无法有效辨识出动态需求下的风险路段，因为在不同的需求下路段的风险排序结果近乎一致。相比于Welch 模型，本文提出的风险辨识模型评估出的路段48在较高的交通需求下风险有明显的提高。这是因为作为通往高铁站主干路上的关键路段，路段48南北邻接朱宏路快速路，东侧与凤城十路和凤城十二路相连，拓扑连接紧密；当南北侧驶入和驶出高铁站的客流增多、东侧的路段较为拥堵时，易受到相邻路段车流的影响，从而具有较高的功能耦合。此外，Welch 模型计算结果认为路段5 在不同的需求下都具有较高的风险，但实际上其是单向行驶路段，南侧驶入高铁站的客流虽然较大，但北侧高铁站产生的客流只能从西侧的朱宏路驶出，并且与之相连的路段也较少，并未有明显的拥堵现象。由此可知，忽视拓扑和功能耦合的风险评估模型可能无法准确对高铁站周边耦合性较强的网络进行风险辨识。

为进一步分析网络风险的动态变化规律，选取编号为48（朱宏路南段）的重要路段，计算其在不同时段对高铁站周边路网风险的影响程度，并绘制2019 年4 月21 日5：00—10：00 和15：00—20：00的网络风险变化曲线，如图7和图8所示。

由图7 可看出，路段48 在6:20—6:30 对周边路网影响较大，因为该路段北侧有公交充电站，大量的公交车会在此时段发车，不仅造成路段无法正常通行，还会延长交通网络中用户的平均出行时间，增加网络的运行风险。另外，由图8 可看出，该路段在18:00 左右也会造成交通网络风险明显增加，这可能是由于晚高峰车流增多和路段周边施工围挡，造成南北两侧的交叉口出现拥堵，降低了网络的运行效率。

图7 早高峰动态风险变化曲线图

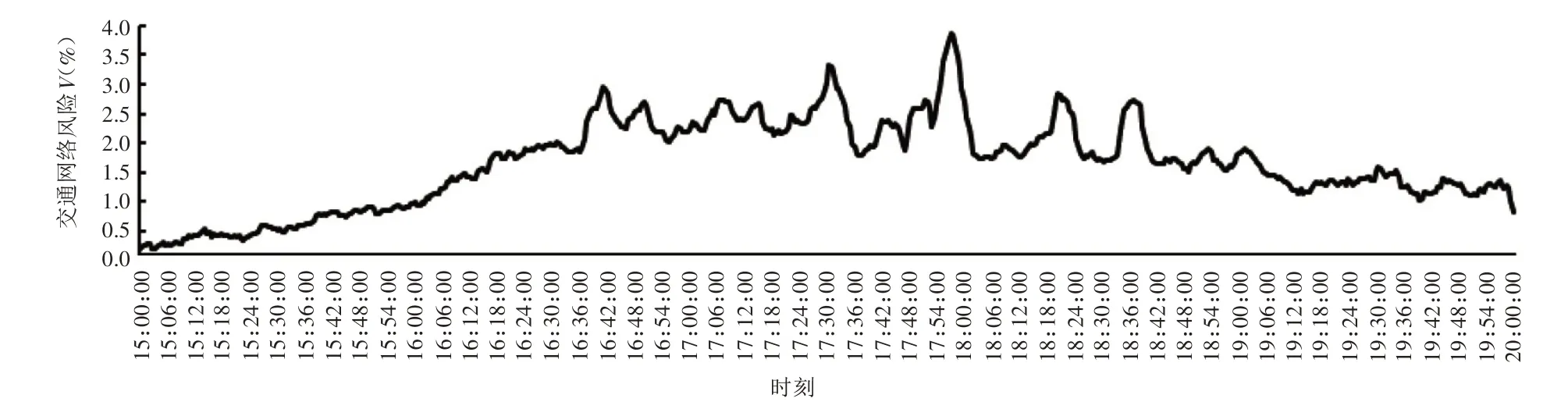
图8 晚高峰动态风险变化曲线图

综上，本文所提的动态耦合风险辨识模型相比于传统的Welch 模型，考虑了网络拓扑和功能的耦合，对于高铁站周边这种具有短时高强度集散特征的路网的风险变化更为敏感，可准确识别出对网络风险影响较大的节点和路段，并实时将局部路网风险量化，有助于交通网络风险动态预警和缓解高铁站周边路网拥堵。

3 结语

相比于普通城市路网，高铁站周边路网具有交通集散需求高和路网单元耦合作用显著等特点。当交通出行需求较高时，不仅存在局部路段拥堵现象，还会显著提高整个网络的运行风险。鉴于此，本文在考虑网络拓扑结构和功能特征的基础上，还重点考虑了网络单元的耦合作用，构建了适用于高铁站周边路网的动态耦合风险辨识模型，同时分析了不同交通需求下高铁站周边路网的风险动态变化情况。研究表明不同交通需求下高铁站周边路网风险变化呈现出明显的时空差异性，距离高铁站较近且耦合作用较强的主干路和交叉口对网络风险影响较大；随着交通需求的增大，网络单元风险也逐渐升高；不同网络单元失效后对用户平均出行时间损失的影响也具有显著性差异。考虑到用户出行行为和路网空间结构的区域异质性，本研究的网络风险评估方法在适用范围仍具有一定局限，未来将对不同城市不同功能区域的路网风险进行研究，以期制定综合的风险评价方案来保障城市路网的高效运行。