不确定性条件下地下水污染监测井网优化设计——基于XGBoost替代模型
董广齐,卢文喜*,范 越,潘紫东
不确定性条件下地下水污染监测井网优化设计——基于XGBoost替代模型
董广齐1,卢文喜1*,范 越2,潘紫东1
(1.吉林大学新能源与环境学院,吉林 长春 130012;2.长江科学院,湖北 武汉 430010)
在地下水污染监测井网优化设计中,应用模拟优化方法时客观存在的模型参数不确定性往往会影响到设计监测井网的可靠性.针对该问题,重点考虑了渗透系数和污染源释放强度的不确定性,应用模拟优化方法和蒙特卡罗方法求解上述不确定性参数影响下的最优监测井布设方案.为缓解蒙特卡罗方法多次调用模拟模型所产生的巨大计算负荷,本研究建立了XGBoost替代模型,代替模拟模型与优化模型进行耦合.为提高监测井网对实际污染羽的监测精度,污染监测井网优化模型以监测空间矩误差极小化为优化目标.此外,本次研究还考虑了监测井网设计中污染源释放强度的动态变化过程.最后,以抚顺市某煤矸石堆放场地为基础建立假想例子,验证所提方法的有效性.结果表明:1.XGBoost能够有效近似模拟模型的输入输出关系,显著降低了计算负荷.2.空间矩能够有效评估监测井网插值污染羽和实际污染羽的逼近程度,优化设计后的监测井网能够较为准确地捕捉到实际污染羽的状态.3.模拟优化方法结合蒙特卡罗方法能有效求解不确定性条件下最优监测井网的设计问题.本文为地下水污染监测井网设计提供了一种稳定可靠的方法.
地下水污染;监测井布设;模拟优化方法;不确定性;XGBoost替代模型
地下水污染具有存在的隐蔽性、发现的滞后性、修复困难等特点,在污染治理和修复的过程中建立相应的地下水污染监测网络,可以及时地获取地下水污染资料,从而为污染修复工作提供数据支持和检验保障.然而,由于地下水监测井网的建设成本高昂,监测工作的展开需在有限的资金条件下获得更多的地下水有效信息,因此对地下水污染监测井网进行优化设计就显得十分必要.其基本目的是在一定的人力,物力,资金限制下,获取最具有代表性的地下水水质时空分布信息,找到最经济有效的监测井布设方案.
模拟优化方法将地下水数值模拟与运筹学中的优化方法相结合,使得其既能够以地下水系统固有的物理规律为基础来预测地下水位、水质的分布趋势,又能够在满足各种环境、经济、技术等要求的前提下获得最优的井位布设方案[1].国内外基于模拟优化方法对监测井网优化设计的研究有很多.Meyer等首次考虑了不确定性条件下监测井网的设计,运用模拟-优化方法以最大化检出概率为目标,确定了监测井网的位置[2].Reed以提高监测井网监测精度为目的对优化模型的目标函数进行改进,以全局质量评估误差最小,监测成本最小为目标函数,结合反距离权重法和普通克里格法进行插值,建立了地下水污染的长期监测网络[3].Wu基于Reed的研究,在目标函数中增加了污染羽一阶矩阵和二阶矩阵评估,提高监测井网插值对实际污染羽的拟合精度,并建立了更为有效的监测井网络[4].骆乾坤整合前人在目标函数上的研究成果,建立了包括监测费用评估、质量评估和空间矩评估在内的多目标优化模型,并用改进小生境Pareto遗传算法(NPGA)进行求解,充分揭示了监测费用和监测精度之间的权衡关系[5].范越以最大覆盖高污染区域为监测方案优化目标并应用蒙特卡罗方法,在污染监测井优化设计中考虑了渗透系数不确定性带来的影响[6].罗建男应用模拟优化法并结合0-1整数规划模型,对某垃圾填埋场地下水质监测井进行优化设计,取得了很好的结果[7].
尽管前人在监测井网的优化设计上已取得了很大的进展,在优化模型的形式,优化目标的选取,优化模型的求解等方面均有较为广泛的研究,但长期以来研究者对于不确定性的研究往往只局限于污染源信息或者模型参数的单一角度,缺少对于二者的综合分析,针对该问题本文同时对污染源释放强度和模拟模型渗透系数的不确定性进行了研究,运用蒙特卡洛方法对两者共同影响下的地下水污染监测井网进行优化设计.此外,过去的文献一般仅针对释放强度恒定的污染源,而对释放强度随时间变化的污染源少有涉及,因此本文对释放强度非恒定的污染源情形进行了研究.最后,在应用蒙特卡罗方法时,需要多次调用模拟模型,势必会产生极大的计算负荷,而替代模型能够以较小的计算量近似拟合模拟模型的输入输出关系,在蒙特卡洛分析中直接调用替代模型而不是模拟模型可以大幅减小计算负荷,减少计算时间.传统的替代模型构建方法(如Kriging、支持向量机、BP神经网络等[8-9])属于浅层机器学习,在简单问题上拟合效果较好,但对于复杂条件下模拟模型存在的非线性映射关系拟合精度还有待提高.学习能力更强的深度神经网络方法(如卷积神经网络[10]、循环神经网络、深度置信神经网络等)的非线性表达能力更强,但缺点是依赖数据驱动,需要建立较大的样本集,同时模型设计复杂,不够轻量化,容易出现过拟合现象.XGBoost(极限梯度提升树)是基于决策树的集成机器学习算法,通过组合多个简单的弱分类器形成了一个学习能力更强的强分类器并且构造形式简单,其次引入了叶节点惩罚函数有效避免了模型的过拟合,最后它对数据量的要求较低,在中小型数据集中也能有较好的表现.目前为止尚未见到应用XGBoost方法建立地下水数值模拟模型的替代模型的报道,亟需进行实例验证.因此,本研究采用XGBoost方法拟合多维不确定变量下的模拟模型,研究其在多维输入多维输出情况下的拟合效果.
综上,本文基于模拟优化方法建立了以最大化污染监测精度为优化目标的地下水污染监测井网优化模型,采用蒙特卡罗方法研究渗透系数和污染源释放强度不确定性对监测井网优化设计的影响,并同时考虑了污染源释放强度的动态变化过程.为减小求解过程中的计算负荷,应用XGBoost方法构建模拟模型的替代模型.最后以抚顺市某煤矸石堆放场为基础建立假想例子验证了方法的有效性.研究结果可为地下水污染监测井网的布设提供方法依据.
1 模拟优化方法
模拟优化方法的本质是将模拟模型和优化模型进行耦合.模拟部分即建立地下水污染质运移模拟模型,反映地下水系统本身固有的物理规律;优化部分即根据实际的优化目标构建合适的目标函数,进而建立优化模型.本次研究采用嵌入法对两者进行耦合,将模拟模型(或其替代模型)作为约束条件嵌入优化模型.而建立模拟模型是应用模拟优化方法的基础.
1.1 地下水污染质运移模拟模型
1.1.1 地下水水流模型的建立 根据研究区水文地质概念模型,建立研究区二维潜水模型,如下所示:


1.1.2 地下水污染质运移模型的建立
在地下水水流数值模型基础之上,建立二维地下水污染质运移数学模拟模型:
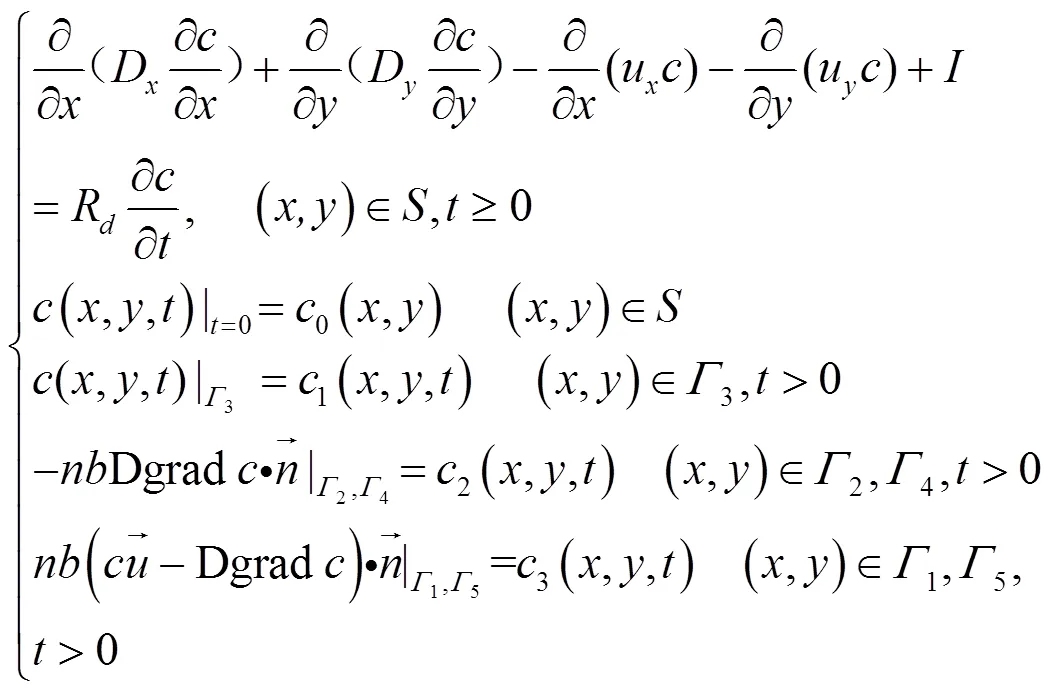
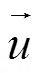
1.2 模拟模型的XGBoost替代模型
替代模型能够以较小的计算量近似逼近模拟模型的输入输出关系,通过对一定数量的已知样品特征的输入-输出关系进行拟合(训练样本),来构建模拟模型的拟合函数,用于预测未知样品的特征输出响应[11],在应用蒙特卡洛方法处理不确定性问题时,替代模型能够大幅度降低计算负荷提高计算效率.
XGBoost是基于决策树的集成机器学习算法,在非结构数据(图像、文本等)的预测问题中,人工神经网络数据的表现要优于其他算法或框架,但在处理中小型结构数据或表格数据中,基于决策树的算法表现更为优异[12].XGBoost近年来在机器学习领域表现出众,是机器学习赛事Kaggle中大多数冠军方案的主体算法,已经应用在多个工业前沿中[12-14].
XGBoost[15]以CART(分类回归树)为基础. CART通过建立迭代过程不断地将特征空间通过二叉树划分为若干单元,每一个特征单元(叶节点)对应于一个输出(一个简单的二层CART切分过程如图1所示).通过不断优化特征空间的切分方式(切分特征和切分点)和各特征单元的输出值,使回归树输出和已知输出误差最小,进而对数据集进行拟合.CART有一个较为显著的缺点,对于一个训练集特征空间易划分的过于详细,导致过拟合的现象,泛化能力较差.
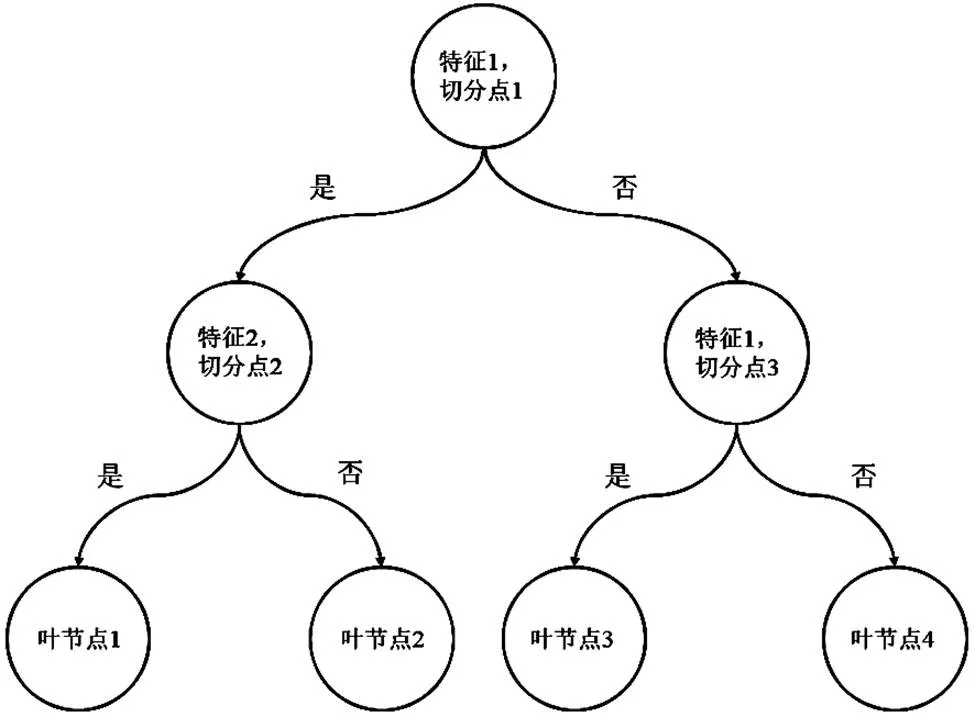
图1 二层CART切分示意
XGBOOST算法弥补了CART的不足,采用集成思想,线性组合多个CART,将上一棵树的拟合误差作为下一棵树的拟合目标,通过不断加入新的回归树使预测值不断逼近已知值.
该过程如下所示:
●初始化(模型中没有树):
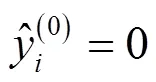
●在模型中插入第1棵树:
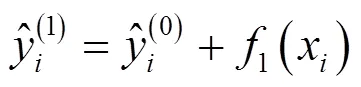
●在模型中插入第2棵树:

●在模型中插入第棵树:

在明确了XGBoost组合多个CART的过程后,还需要进一步确定模型中各个CART的构建方法.XGBoost采用以下目标函数对决策树的切分特征、切分节点和各叶节点的输出值进行优化.
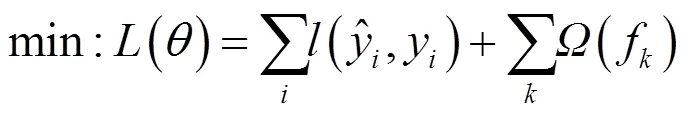
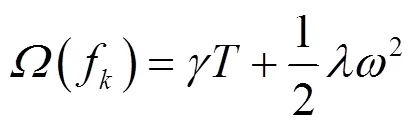
本文以5个不确定性变量作为输入(各应力期污染源释放强度1、2、3,两分区渗透系数1、2),以各潜在监测井的污染质浓度作为输出,建立XGBoost替代模型,算法基于Python语言实现.
1.3 优化模型
地下水污染监测井网的优化设计问题可以近似概化为运筹学中经典的离散选址问题.在研究区中根据实际情况预先设置可以建设监测井的潜在监测井位置,而后从中挑选出信息量较大的监测井,这可以应用0-1整数规划模型进行表示,潜在井被选中取1,否则取0.本次研究的优化目标是最大化污染监测信息量.如果设计监测井网的监测数据经过克里格插值方法得到的插值污染羽和实际污染羽越相近,那么监测井网的选址越好,地下水污染监测信息量越大,否则监测数据包含无效信息,应进行监测井优化,删除冗余井,增加有效的控制井.但事实上,实际污染羽的形态很难得到,通常可以根据已有地质和水文地质信息建立数值模拟模型,求得模拟模型污染羽并用其代替实际污染羽.因此,优化问题转化为怎样甄选出信息量大的潜在监测井,组合成合适的监测井网,使监测井网插值污染羽和模拟模型污染羽更为相近.
在进行实际优化求解过程中,需要将两种污染羽的逼近程度进行数学化表达,建立评估监测有效信息量的数学表达式.污染羽状态以浓度为基础可以处理成一个灰度图像,两种污染羽逼近程度的评估可以转化为图像的相似性评估.空间矩可以较为准确地描述图像的空间特征,它包括零阶矩、一阶矩和二阶矩.零阶矩可以代表污染羽的质量,一阶矩代表污染羽的重心位置,二阶矩代表污染羽的形状特征.只有同时知道这3种不同的物理特征,才能准确地描述污染羽流的分布[5].
污染羽的零阶矩(全局质量)、一阶矩(重心位置、二阶矩(污染羽形状特征)公式如下所示:
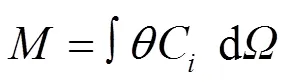


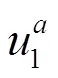
对于模型中渗透系数和释放强度的不确定性问题,应用蒙特卡罗方法,通过多次运转替代模型将模型参数的不确定性转化为了实际污染羽形态的不确定性.而后进一步计算不同污染羽形态下的空间矩误差,优化模型的优化目标为各污染羽形态下空间矩误差的总和最小,由此加强了监测井网优化结果的鲁棒性,保证了其在不确定参数的整个取值范围内都能表现较好.在以上基础上,建立污染监测井网优化模型,数学表达式如下:



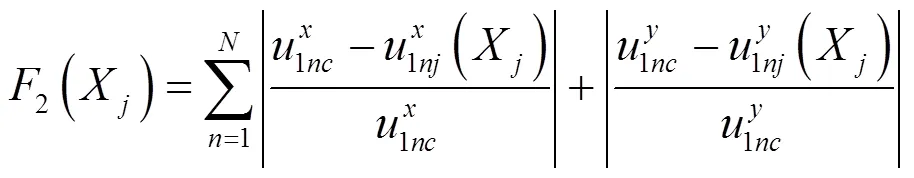
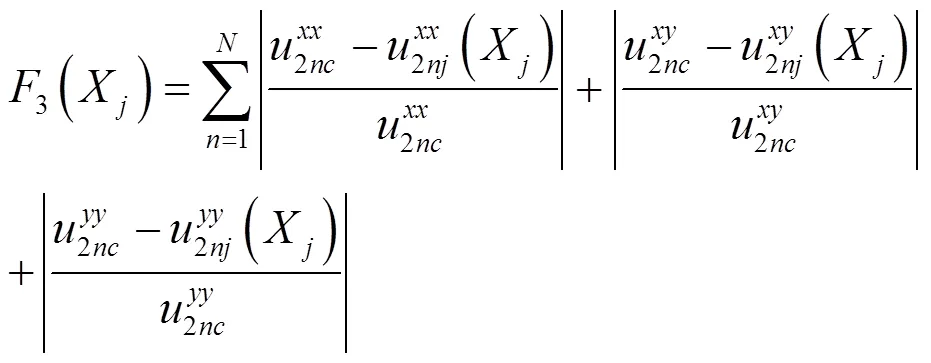
2 案例应用
2.1 问题概述
研究区域为抚顺市某煤矸石渗漏区,东西长约9700m,南北约6100m,总面积约为52.35km2.由于长期进行煤生产活动,大量堆放的煤矸石随着降雨入渗向地下水中泄漏污染物,在当地引起了严重的地下水污染,依据《地下水质量标准》(GB/T 14848- 2017)[16],研究区地下水水质已达V类.本文将硫酸根离子作为典型污染物,模拟研究区概况如图2所示,本次研究的主要含水层为一层8m厚的潜水含水层,研究区根据水文地质参数的非均质性可划分为两个区域,概化为非均质各项同性含水层,地下水流可概化为二维非稳定流.煤矸石渗漏区概化为面状污染质源汇项.研究区北部G1为浑河边界,概化为给定水头边界;东北部边界G2和南部边界G4为隔水岩层,概化为隔水边界;将东部边界G3概化为侧向径流补给边界,西南部边界G5概化为侧向径流排泄边界.在溶质运移模型中,根据实际情况以硫酸根作为模拟污染质,研究区北部边界G1和西南部边界G5概化已知对流-弥散通量边界;东北部边界G2和南部边界G4概化为零通量的水动力弥散边界;东部边界G3概化为已知浓度边界,地下水总体由东南向西北方向流动.

图2 研究区概况
在数值模型建立后,采用2017年10月的水位、水质数据进行模型校正,采用2018年10月的水位、水质数据进行模型检验.在模型的校正和检验过程中,水头的观测值和模拟值误差小于0.5m,污染质浓度观测值和模拟值的相对误差小于10%,模型校正和检验的准确度均满足要求,两分区渗透系数校正结果分别为82.7m/d和97.4m/d.此外,根据污染物的释放时间和观测浓度,运用溶质运移模型进行反演识别,获得煤矸石向地下水泄漏硫酸根的释放强度大约为7000mg/d.研究区各水文地质参数校正值见表1.
在以上实际场地的基础上建立假想例子.相关部门对煤矸石堆污染物进行阶梯性修复,10内其污染源释放强度逐渐降低,预计释放强度为1~ 47000mg/d,5~74000mg/d,8~101000mg/d,本次研究为对10后的修复效果检验提供数据支持,设计监测井网拟合10后地下水污染羽状态.
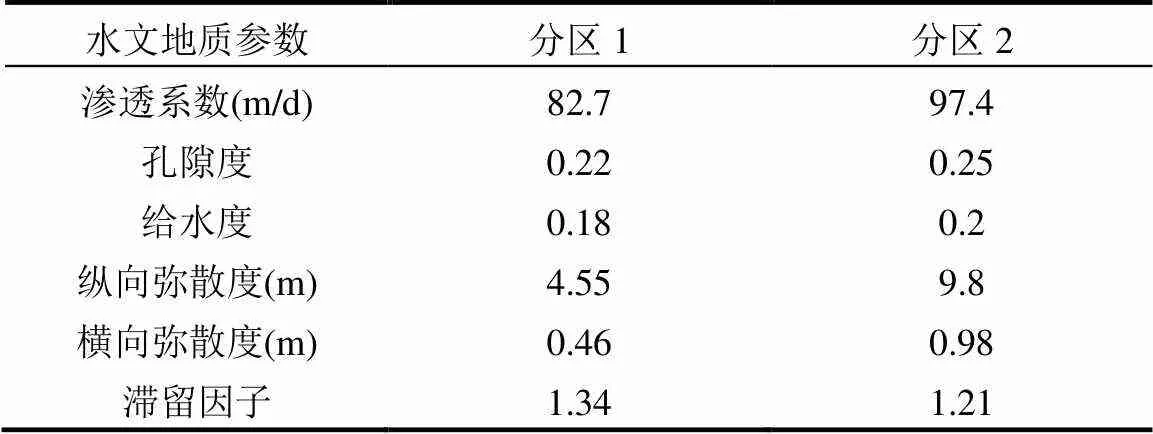
表1 模型校正后研究区水文地质参数表
煤矸石堆污染源的释放强度受多种因素影响,如降水强度、降水持续时间、人类活动等,渗透系数在空间上同样具有一定的变异性,因此污染物释放强度和渗透系数均具有一定的不确定性,这两者都会对地下水污染井网设计产生较大影响.
因此,本文同时考虑污染源3个应力期释放强度和2个分区渗透系数的不确定性,采用了蒙特卡洛方法对10后的地下水污染监测井网进行设计,根据实际场地条件确定50口潜在监测井,其在煤矸石渗漏区的地下水下游区域分布较密,在上游区域分布较稀疏,从中选取合适的监测井构建地下水污染监测井网,最大化地下水污染监测精度.
不确定性变量大致变化范围依据专家经验如表2所示.

表2 不确定参数分布范围
在本案例中,研究区污染物浓度场使用GMS中MODFLOW和MT3DMS模块进行计算.
2.2 XGBoost替代模型的建立
本文在研究区内设置50口潜在监测井,从中选取合适的监测井构建地下水污染监测井网.因此替代模型的输入向量为污染源3个应力期的释放强度以及两个分区的渗透系数(1、2、3、1、2),输出向量为50口潜在监测井处的硫酸根浓度.
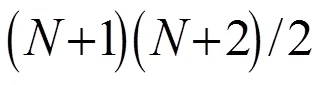
本文采用R2(决定系数)和MRE(平均相对误差)两个指标衡量替代模型的拟合效果,其中MRE的数学表达式如下:

式中:为样本组数;y为模拟模型输出值;y为替代模型输出值.

表3 5折交叉验证中5次训练的评价结果
为了更好的评估模型的拟合能力,减少随机误差带来的影响,提高样本信息利用率,采用折交叉验证方法对模型进行交叉验证,该方法将样本集平均分割为个互斥子集,每次选择(-1)个子集作为训练集,1个子集作为测试集;重复多轮计算,保证每个子集都被且仅被作为一次测试集,最终获得个测试结果,并输出其平均值作为拟合精度[18].在本次研究中,取折数为5,5次训练后所得评价指标及平均值见表3.其中Fold-4表现最好,该次训练替代模型和模拟模型的拟合结果如图3所示.5次训练2和MRE的平均值分别为0.995和0.87%,说明XGBoost替代模型的拟合精度较高.
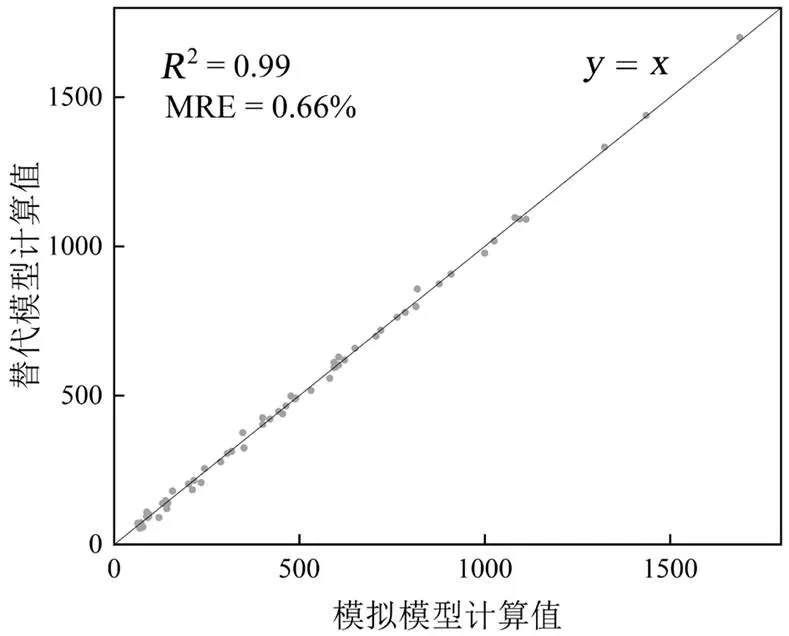
图3 替代模型与模拟模型的拟合结果
2.3 优化模型的建立和求解
在对XGBoost模型进行交叉验证后,选取训练表现最好的一次作为模拟模型的替代模型.而后运用拉丁超立方抽样(LHS)在不确定变量分布范围内抽取1000组输入样本,将其带入到替代模型而不是模拟模型中进行求解,得到各潜在监测井的硫酸根浓度,从而获得不确定条件下的1000组污染羽.
根据上文中优化模型构建方法,建立最大化污染监测精度的监测井网优化模型,优化目标为最小化1000组污染羽的空间矩误差总和,优化模型具体的数学形式如下:




式中:第一个约束条件是模拟模型的替代模型,该约束条件使整个优化模型满足地下水系统本身固有的物理规律;第二个约束条件为监测井的限制个数;第三个约束条件表示决策变量是0-1整数变量.

图4 不同监测井总数下的最优布设方案
该优化模型运用MATLAB平台的遗传算法工具箱进行求解,获得了不同监测井总数下的最优布设方案,如图4所示.此外,运行GMS求解地下水溶质运移模型平均单次耗时约为2min,如直接使用模拟模型进行不确定性分析,需要计算模拟模型1000次,总计耗时33h.而运用替代模型代替模拟模型则只需运行模拟模型100次获取输入-输出样本集,总耗时3.3h,替代模型的输出约需2~3s,可忽略不计.因此,利用替代模型进行1000次蒙特卡洛实验,可节省90%的计算时间.
2.4 优化结果的检验
本模型的目的是在渗透系数和污染源释放强度不确定的条件下最大化地下水污染监测精度,最后应当对优化结果进行检验.
选取各输入变量的标准值作为输入对优化结果进行检验,即污染源释放强度为7000(1~4)、4000(5~7)、1000(8~10)mg/d,两个分区的渗透系数分别为82.7m/d(区1)和97.4m/d(区2).其余水文地质条件不变,运用GMS进行求解,获得10后的模拟污染羽.而后将模拟污染羽与监测井布设方案得到的插值污染羽进行相似性评估,评估指标采用零阶矩、一阶矩、二阶矩,两污染羽空间矩的相对误差如表4所示,模拟污染羽与监测井网插值污染羽的对比如图5所示.
可以看出,随着监测井数量的不断增加,插值污染羽与模拟污染羽的误差评估指标都在不断降低,其中二阶矩敏感性最强,下降最为明显.当监测井数量为18口时,全局质量误差(m)为2.27%,质心相对误差(1)为1.07%,二阶矩相对误差(E2)为10.91%,拟合效果较好,结合污染羽对比图(图5)也可以看出,监测井网设计方案的插值污染羽能够相对精确地刻画实际污染羽的浓度、位置、形状.在污染质浓度大的区域,监测井布设密集,反之稀疏,且随着监测井数目的增加,刻画精度越来越高.本次研究为污染监测井网的优化设计提供了一种稳定可靠的方法.

表4 各个监测方案模拟污染羽与插值污染羽的空间矩相对误差
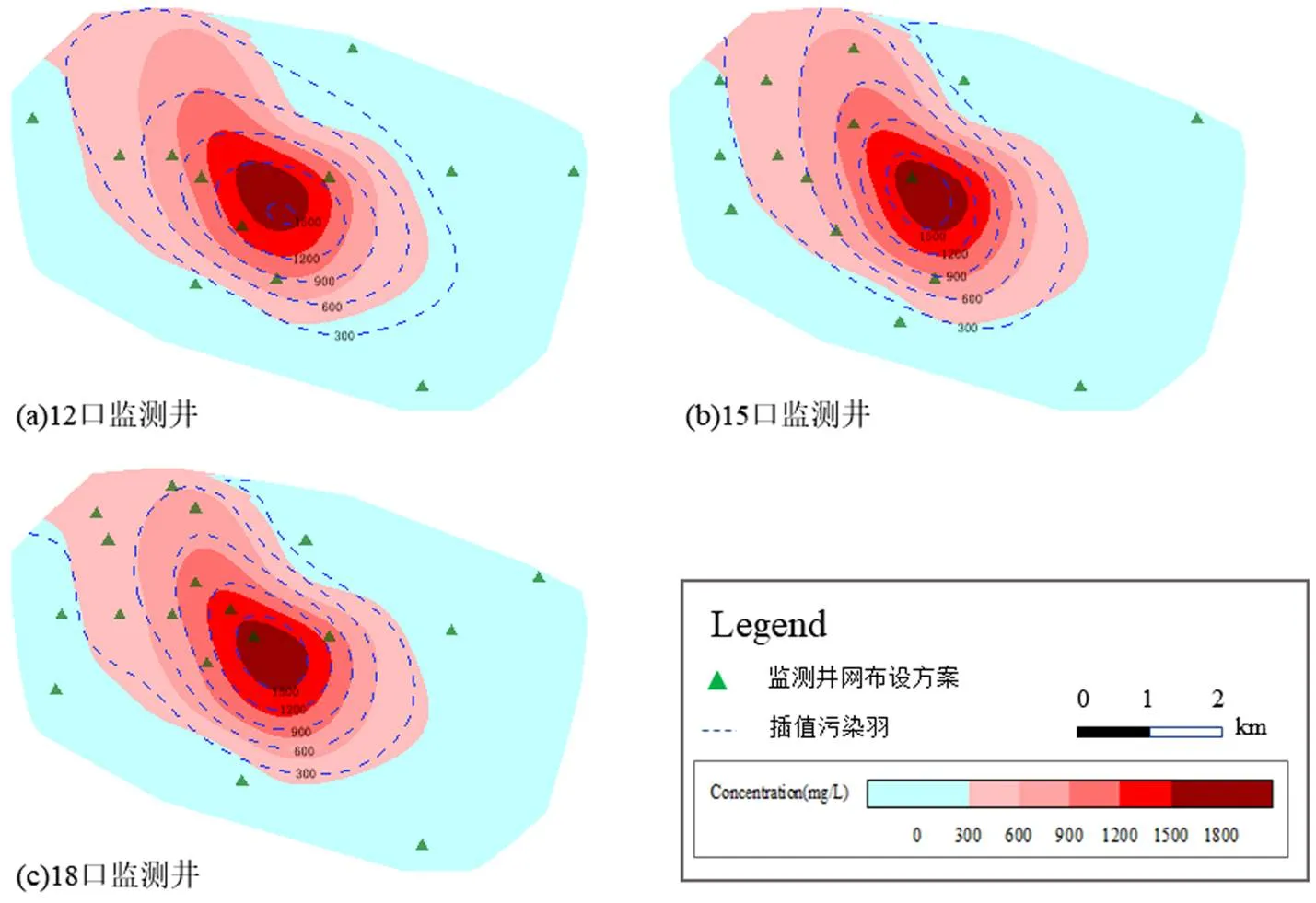
图5 不同监测方案下模拟污染羽和插值污染羽的对比
3 结论
3.1 运用XGBoost方法建立模拟模型的替代模型精度较高,能有效近似模拟模型的输入输出关系,显著降低了计算负荷.因此,在运用蒙特卡罗方法分析不确定性时,使用XGBoost替代模型代替模拟模型与优化模型进行耦合是可行的.
3.2 空间矩图像评估方法能有效评估监测井网插值污染羽和实际污染羽的逼近程度,在以空间矩误差极小化为目标函数进行监测井网优化设计时,最优监测方案能够较为准确地捕捉到实际污染羽的形态.
3.3 将0-1整数规划和模拟模型相结合的模拟优化方法,能够从一系列潜在监测井中选择合适位置构建监测井网.将蒙特卡罗方法和模拟优化方法相结合,可以用来求解不确定性条件下污染监测井网的最优布设方案.
[1] 卢文喜.地下水系统的模拟预测和优化管理[M]. 北京:科学出版社, 1999:104-105.
Lu W X. Groundwater system simulation prediction and optimization management [M]. Beijing: Science Press, 1999:104-105.
[2] Meyer P D, Brill Jr E D. A method for locating wells in a groundwater monitoring network under conditions of uncertainty [J]. Water Resources Research, 1988,24(8):1277-1282.
[3] Reed P, Barbara M, Albert J V. Cost-effective long-term groundwater monitoring design using a genetic algorithm and global mass interpolation [J]. Water Resources Research, 2000,36(12):3731-3741.
[4] Wu J F, Zheng C M. Cost-effective sampling network design for contaminant plume monitoring under general hydrogeological conditions [J]. Journal of Contaminant Hydrology, 2005,77:41-65.
[5] 骆乾坤,吴剑锋,林 锦,等.地下水污染监测网多目标优化设计模型及进化求解[J]. 水文地质工程地质, 2013,40(5):97-103.
Luo Q K, Wu J F, Lin J, et al. An evolutionary-based multi-objective optimization model for groundwater monitoring network design [J].Hydrogeology & Engineering Geology, 2013,40(5):97-103.
[6] 范 越,卢文喜,欧阳琦,等.基于Kriging替代模型的地下水污染监测井网优化设计[J]. 中国环境科学, 2017,37(10):3800-3806.
Fan Y, Lu W X, Ouyang Q, et al. Optimum design of groundwater pollution monitoring well network based on Kriging surrogate model [J]. China Environmental Science, 2017,37(10):3800-3806.
[7] 罗建男,李多强,范 越,等.某垃圾填埋场地下水质监测井网优化设计——基于模拟优化法[J]. 中国环境科学, 2019,39(1):196-202.
Luo J N, Li D Q, Fan Y, et al. Optimization of groundwater quality monitoring network at a landfill——based on simulation optimization method [J]. China Environmental Science, 2019,39(1):196-202.
[8] 邢贞相,曲睿卓,赵 莹,等.不同替代模型在地下水污染源释放历史反演中适用性研究[J]. 东北农业大学学报, 2018,49(12):59-68.
Xing Z X, Qu R Z, Zhao Y, et al. Applicability study of different surrogate models in retrieving release history of groundwater contaminant sources [J]. Journal of Northeast Agricultural University, 2018,49(12):59-68.
[9] 潘紫东,卢文喜,范 越,等.基于模拟-优化方法的地下水污染源溯源辨识[J]. 中国环境科学,2020,40(4):1698-1705.
Pan Z D, Lu W X, Fan Y, et al. Inverse identification of groundwater pollution source based on simulation-optimization approach [J]. China Environmental Science, 2020,40(4):1698-1705.
[10] 莫绍星.基于深度学习的地下水模拟高维不确定性分析和反演[D]. 南京:南京大学, 2019.
Mo SX. Towards Efficient high-dimensional uncertainty quantification and inverse analysis in groundwater modeling using deep learning [D]. Nanjing: Nanjing University, 2019.
[11] 侯泽宇,卢文喜,王 宇.基于替代模型的地下水DNAPLs污染源反演识别[J]. 中国环境科学, 2019,39(1):188-195.
Hou ZY, Lu WX, Wang Y. Surrogate-based source identification of DNAPLs-contaminated groundwater [J]. China Environmental Science, 2019,39(1):188-195.
[12] 何 龙.深入理解XGBoost:高效机器学习算法与进阶[M]. 北京:机械工业出版社, 2020:6-8.
He L. Deep understanding of XGBoost: efficient machine learning algorithms and advanced problem [M]. Beijing: China Machine Press, 2020:6-8.
[13] 陈振宇,刘金波,李 晨,等.基于LSTM与XGBoost组合模型的超短期电力负荷预测[J]. 电网技术, 2020,44(2):614-620.
Chen Z Y, Liu J B, Li C, et al. Ultra Short-term Power Load Forecasting Based on Combined LSTM-XGBoost Model [J]. Power System Technology, 2020,44(2):614-620.
[14] 赵洪山,闫西慧,王桂兰,等.应用深度自编码网络和XGBoost的风电机组发电机故障诊断[J]. 电力系统自动化, 2019,43(1):81-86.
Zhao H S, Yan X H, Wang G L, et al. Fault diagnosis of wind turbine generator based on deep autoencoder network and XGBoost [J].Automation of Electric Power Systems, 2019,43(1):81-86.
[15] Chen T, Guestrin C. XGBoost: a scalable tree boosting system [C]// Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. San Francisco, California, USA: Association for Computing Machinery, 2016:785–94.
[16] GB/T 14848-2017 地下水质量标准 [S].
GB/T 14848-2017 Standard for groundwater quality [S].
[17] Jin Y. A comprehensive survey of fitness approximation in evolutionary computation [J]. Soft Computing, 2005,9(1):3-12.
[18] 张钧博,何 川,严 健,等.基于交叉验证的XGBoost算法在岩爆烈度分级预测中的适用性探讨[J]. 隧道建设, 2020,40(S1):247-253.
Zhang J B, He C, Yan J, et al. Discussion on the applicability of XGBoost algorithm based on cross validation in prediction of rockburst intensity classification [J]. Tunnel Construction, 2020,40 (S1):247-253.
[19] Fan Y, Lu W X. Optimal design of groundwater pollution monitoring network based on the SVR surrogate model under uncertainty [J]. Environmental Science and Pollution Research, 2020,27:24090–24102.
[20] 黄满红,顾国维.地下水环境监测系统的设计[J]. 环境监测管理与技术, 2003,15(1):13-15.
Huang M H, Gu G W. The design about environmental monitoring system of underground water [J].The Administration and Technique of Environmental Monitoring, 2003,15(1):13-15.
[21] Philip D M, Albert J V, Eheart W. Monitoring network design to provide initial detection of groundwater contamination [J]. Water Resources Research, 1994,30(9):2647-2659.
Optimal design of groundwater pollution monitoring network under uncertainty.
DONG Guang-qi1, LU Wen-xi1*, FAN Yue2, PAN Zi-Dong1
(1.College of New Energy and Environment, Jilin University, Changchun 130012, China;2.Yangtze River Scientific Research Institute, Wuhan 430010, China)., 2022,42(5):2144~2152
When applying the simulation-optimization method, objective parameter uncertainty will usually affect the reliability of the design result of groundwater pollution monitoring network. For this problem, the study simultaneously considered the uncertainty of hydraulic conductivity and emission intensity of pollution source, applying Monte Carlo method to design the optimal monitoring wells scheme under the influence of model uncertainty. But Monte Carlo method need to invoke the simulation model many times which will cause a huge amount of calculation. To reduce the calculation load, the study proposed to use Extreme Gradient Boosting (XGBoost) method to construct the surrogate model replacing the simulation model to couple the optimization model in the optimal design of GPMN. To sufficiently improve the monitoring precision of GPMN, the optimization model applied error of spatial moment as objective function. Besides, the dynamic change of emission intensity of pollution source was also considered. Finally, we proposed a hypothetical example based on a coal gangue pile in Fushun City to verify the validity of the method. The results are demonstrated: 1.the XGBoost surrogate method can fit the input-output relationship of the simulation model to a high degree with less computation. 2.spatial moment can effectively assess the approximation degree between interpolation pollution plume of GPMN and actual pollution plume, through which the optimized monitoring network can accurately depict actual pollution plume 3.the simulation-optimization method combines Monte Carlo method can solve the problem of the design of GPMN under uncertainty. In conclusion, the paper provides a stable and reliable method for the design of GPMN.
groundwater pollution;monitoring wells network design;simulation-optimization method;uncertainty;XGBoost surrogate model
X523,X830
A
1000-6923(2022)05-2144-09
董广齐(1998-),男,河南信阳人,吉林大学硕士研究生,主要从事地下水污染监测井网优化设计研究.
2022-10-27
国家自然科学基金资助项目(41972252);国家科技部重点研发计划项目(2018YFC18000405)
* 责任作者, 教授, lwx999@163.com
——以J油田M区为例

