面向社交网络中影响力传播研究进展

李 阳

(国家信息中心 北京 100045)

1 影响力概述

影响力的研究最初从商业领域开始，随着社交网络应用的快速普及，影响力的研究也逐渐从应用场景向理论探索不断深入.

1.1 研究背景

随着社交网站及其相关应用的快速发展，人们越来越多地将活动转移到社交网络中，如在Twitter、Facebook和新浪微博上关注朋友和名人的最新动态.社交网络也提供了一个合适的机会，可以进行快速的信息扩散.例如，许多公司在新浪微博、Twitter、Facebook等网站上投放他们的新产品、品牌广告或者发布公共信息.公司开发了新产品，希望投放到市场，因此有限地选取一些高影响力用户，通过这些用户向他们的朋友以及朋友的朋友推荐该产品.公司希望通过这种口口相传的方式最大化地影响社交网络上的用户，使得他们最终购买该产品.社交网络的影响力传播过程如图1所示:

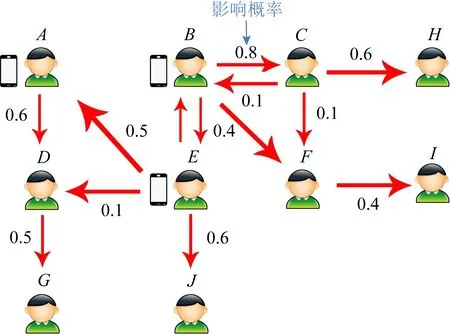
图1 社交网络的影响力传播过程

1.2 影响力概念

影响力通常是指用一种别人所乐于接受的方式来改变他人思想和行动的能力[1].在社交网络上，影响力泛指用户的行为可以影响其朋友或者粉丝也作出类似的行为.基于微观角度进行思考，从用户的历史数据或者静态属性展开分析，对用户之间的影响力进行量化反映了用户以多大概率或者多大程度来影响其朋友或者粉丝采取类似的行为.

1.3 影响力问题描述

面向影响力问题的研究主要聚焦在影响力最大化(influence maximization, IM)问题，具体可以描述为：给定如图1所示的社交网络图(其中节点代表用户，边代表用户之间的关系)，一个具体的传播模型和节点集规模k，如何选定规模为k的节点集合P最大化地传播影响力，即最终影响的总节点数σ(P)最大化.

2 影响力传播研究进展

研究者们从拓扑结构着手影响力传播研究，随着研究的深入，发现贪心算法可以维持最优的影响力传播范围，成为研究者们改进和优化的焦点.后续为了进一步提升算法的可扩展性，一些启发式算法被接连提出，并在相关实验中得到验证.

2.1 拓扑结构

早期的影响力传播研究从拓扑结构展开，认为具有较好连通性的节点有助于信息传播，因此研究者们认为在网络中处于中心位置或具备某些拓扑性质(如节点的度、中心度等拓扑指标)的节点具有较高的影响力.然而，基于无标度网络的生成特点，高拓扑的节点常常优先被链接，这样就造成节点的影响力覆盖范围重复较大.

2.2 贪心算法

随着社交网络的兴起，研究者们开始从信息传播模型出发，在社交网络中模拟信息传播，根据传播范围来度量节点的影响力.Domingos等人[2-3]提出社交网络中个人的网络价值概念，并对影响力定义为：基于预知的信息传播模型，从初始节点出发的信息能传播到达的范围.通常采用的信息传播模型包括线性阈值(linear threshold, LT)模型[4]和独立级联(independent cascade, IC)模型[5]，其中节点状态一般分为激活态和未激活态.在IC模型中，每个边具有1个激活概率，激活节点独立激活其处于未激活状态的邻居.在LT模型中，每个边具有1个影响权重，每个节点随机选择(或预先计算)1个激活阈值，如果该节点的已激活邻居节点的影响权重之和大于该节点的激活阈值，则认为该节点被激活.

基于上述2个模型，Kempe等人[6]系统地讨论了求解影响力最大化问题的时间复杂度是NP-Hard的，但可以通过贪心算法在多项式时间内求得近似最优解.实验表明贪心算法在不同模型上获得的解集明显优于基于拓扑结构的解集，主要缺点是时间复杂度过大，因此研究者们陆续提出一些基于贪心算法的优化方案.Leskovec等人[7]提出CELF方法，该方法利用影响力最大化问题目标函数的子模性，有效降低了模拟计算次数，但是其选择范围是整个网络节点，导致其最差时间复杂度等于原始贪心算法.Goyal等人[8]在此基础上进行优化并提出了CELF++算法，进一步减少了蒙特卡罗模拟次数，降低了时间复杂度.Chen等人[9]基于IC模型提出了NewGreedy策略，通过对网络中所有边进行预删的方式，在每轮蒙特卡罗模拟中同时计算各候选节点的影响力收益，但这种方法相较CELF方法仅在第1轮计算中具有优势.

随后，社交网络的拓扑结构被纳入影响力传播的研究中.Wang等人[10]和Cao等人[11]分别提出了CGA方法与OASNET方法，分别利用贪心算法和动态规划方法按社区挑选种子节点，在对节点性能进行蒙特卡罗模拟时仅将影响力局限在该节点所属社区，这样做虽然能降低部分计算开销，但是忽略了社区之间的边损失以及全局性的影响力度量，造成影响力传播范围要弱于Chen等人[9]的NewGreedy策略.Borgs等人[12]提出一个影响力传播估算方法，通过对社交网络的拓扑结构随机生成一个超图，重复地在超图中选择最大度的节点，但是该方法缺乏场景数据的验证.Cohen等人[13]提出一个改进的贪心算法SKIM，针对原始贪心算法的每轮迭代进行优化，有效降低了时间复杂度.Tang等人[14]提出一个2阶段的影响力最大化算法，通过计算初始节点集最大化传播范围的最低边界来进行参数估计和数值采样，进一步降低了时间复杂度，甚至更优于CELF++算法.Wang等人[15]提出一个多路径的异步阈值模型MAT，提出的IV-Greedy算法基于公开数据集在传播范围和运行时间方面取得了较优的性能.

2.3 启发式算法

由于贪心算法的时间复杂度较大, 为了进一步提高算法的可扩展性，研究者们提出了一系列启发式算法，如BentweenessCentrality[16]，k-shell[17]，PageRank[18]，LeaderRank[19]等，用于发现社交网络中的高影响力节点.Chen等人[9]提出DegreeDiscount方法，该方法仅针对均匀IC模型且仅考虑节点对一阶邻居的影响力，在传播概率较小时效果良好.Chen等人[20-21]提出了PMIA方法和LDAG方法，分别基于IC模型和LT模型在真实社交网络中进行实验分析，每轮通过探索局部结构来选择新的种子节点.实验表明这2种方法能获得更好的解集，但影响力传播范围和计算开销容易受拓扑结构影响[22].Kimura等人[23]提出基于最短路径的SPM/SP1M方法，Narayanam等人[24]提出基于Shapley值的方法，虽然这2种方法能够获得较好的解，但可扩展性差.

随着研究方法的不断深入，一些可扩展性强的启发式算法被陆续提出.Jiang等人[25]引入模拟退火算法来解决均匀IC模型上的影响力最大化问题.Goyal等人[26]提出一种针对LT模型的启发式算法Simpath，基于节点的邻接路径来评估节点的影响力，并采用参数来控制影响力传播和运行时间之间的平衡.Jung等人[27]基于影响力排名和影响力估计提出一个启发式算法IRIE，通过对种子节点进行增量影响力预测，降低内存占用空间和运行时间.Zhou等人[28]提出UBLF算法，通过贪心算法构建一个上界函数来降低蒙特卡罗模拟次数，在公开数据上的实验结果表明，当种子节点集较小时，可以较CELF方法获得2～10倍的加速比.Galhotra等人[29]从邻接路径出发设计了一个可扩展的启发式算法，与CELF++算法相比降低了内存占用空间.Galhotra等人[30]提出一个观点累计交互模型(opinion-cum-interaction, OI)，并提出一个2阶段的启发式算法，通过进一步降低运行时间来进行影响力传播.Cordasco等人[31-32]提出一个高效的启发式算法，适用于在树状图、环形图和完全图的拓扑结构中开展影响力计算，并扩展到有向图网络结构中[33].

基于上述工作，研究者们的视角也在不断拓展，如积极探索心理、群体等对传播机理的影响.Zhu等人[34]认为群体心理在影响力传播中发挥着重要作用并提出D-SSA算法，该算法在加权社交网络中可获得近似最优解.Kermani等人[35]考虑节点之间的异质性提出可变的概率传播，针对种子节点集的最小化和传播范围的最大化同时进行约束，提出鲁棒的优化模型进行影响力计算.Wang等人[36]首次在多关系社交网络中研究影响力最大化问题，认为群体对节点的影响要远大于邻居节点的影响.Chen等人[37]运用随机选择模型对节点之间的影响进行概率计算，采用基于马尔科夫决策过程的增强学习对影响力最大化问题进行建模，与随机规划相比可以大幅降低时间复杂度.

3 总结与展望

3.1 总 结

目前研究者们针对影响力最大化问题进行了系统研究，分别立足拓扑结构、贪心算法、启发式算法等形成了一系列的研究成果，在学术界深化了理论基础，在产业界得到了应用实践.但是当前研究还是存在一定的挑战：一方面，当前的传播模型基于经典的IC模型和LT模型进行扩展，不能深入反映用户的兴趣分布、交互行为等特性对影响力传播的影响；另一方面，当前研究多聚焦于静态社交网络的拓扑结构，忽略了网络的生长特性、动态变化等对影响力传播的影响.

3.2 展 望

未来围绕影响力的最大化传播还存在继续深入的研究点，如传播模型的深度构建、大规模网络计算和动态在线计算等.

1)传播模型深度构建.

实际场景中的传播模型机理是复杂的，未来传播模型构建需要进一步的深度刻画：一是研究者们加入主题因素[38-40]的影响进行探索，深化节点之间的主题语义、情感分析等内容属性，运用自然语言、机器学习等技术分析主题因素对传播影响的倾向变化；二是立足节点之间的交互行为、偏好倾向等行为属性，运用统计分析技术探讨行为属性对传播影响的微观作用.

2)大规模网络计算.

根据无标度网络的生长特性，社交网络的节点、链接日益增长，拓扑结构的规模日益增大.截至2022年1月，在全球覆盖国家规模较大的社交网络平台中，Facebook达到约29.1亿用户、YouTube达到约25.62亿用户、WhatsApp达到约20亿用户、Twitter达到约4.36亿用户[41].迭代式的全网模拟计算已经无法满足现实需求，需要更大规模的网络计算：一是面向大规模社交网络的拓扑结构，在有限节点预算的情况下继续设计启发式算法，进一步提升算法稳定性；二是立足传播范围评估问题设计分布式算法，面向影响力传播展开并行计算，进一步降低时间复杂度，以不断适应日益增长的规模需求.

3)动态在线计算.

目前的网络结构研究主要围绕静态网络展开，即节点固定以及节点之间的链接关系固定，但实际场景中的社交网络是实时变化的[42-43].未来一方面围绕动态网络中的变化特性进行统计分析，增量式的在线计算将成为研究的重点；另一方面围绕动态网络中的节点生长与链接关系统计并分析其演化规律，为进一步的网络拓扑预测提供支撑.