变形对双侧鳍线传输特性影响的数值计算

孙 海

(乐山师范学院 数理学院，四川 乐山 614000)

0 引言

鳍线作为一种新型毫米波段的传输线，和微带线相比，因为具有较长的主模截止波长和单模带宽、衰减和损耗较小、色散较弱和固体器件连接容易等特点，在混频器、滤波器和谐振器等微波器件中被大量使用。自1977年Saad等[1]研究对脊鳍线以来，学术界对其研究一直处于较热状态， Beyer[2]使用模式匹配法研究了接地鳍线的特性阻抗和单模带宽。Sharma 等[3]讨论了鳍线设计的经验公式。Zheng等[4]使用了多级理论分析了鳍线的传输特性。但是，在计算非均匀波导结构的传输特性时，全波分析比其他任何方法都能提供更高的精度，因此有限元法和基于边缘的有限元法得到了广泛的应用。Lu等[5]使用了节点有限元方法对鳍线主模电场模式进行了计算。孙海等[6-8]使用有限元法计算了单侧鳍线和对脊鳍线的部分传输特性。以上讨论和计算极大地丰富了鳍线的应用。

实际使用过程中，任何器件都可能出现模型某个区域的变形，鳍线也不例外。鳍线的几何模型变形势必引起其传输特性的改变，故对变形鳍线传输特性的讨论具有较大的意义。关于变形传输线特性的计算问题，最早来源于国内兰州交通大学逯迈、陈小强教授课题组，使用节点有限元方法集中研究了均匀传输线变形对其传输特性的影响，如变形矩形、圆形、梯形、三角形等脊波导和双脊波导[9-17]的传输特性变化，关于非均匀变形传输线传输特性改变的研究尚没有涉及，而非均匀传输线由于填充介质的不均匀性导致在分析和计算过程中具有一定的难度，加之非均匀传输线的应用更加广泛，故本文首先从理论上详细推导了非均匀传输线传输特性计算的基于磁场为工作变量的矢量有限元公式，然后运用推导的公式详细地计算了变形双侧鳍线主模归一化截止波长、单模带宽和电场结构等传输特性，得出了模型变形对双侧鳍线传输特性影响的一些较为重要的结论。

1 原理

本文首先给出了变形前、后双侧鳍线的横截面示意图，如图1所示。

(a) 双侧鳍线

(b) 变形双侧鳍线图1 未变形和变形双侧鳍线的横截面示意Fig.1 Schematic diagrams of cross sections of undeformed and deformed bilateral finlines

图1中的白色部分为真空区域，介电常数为ε0，而网状部分为填充介质区域，介电常数为εr，黑色部分为鳍，模型边界、填充区域和鳍位置、大小由符号a，b，s，t1，t2，d1，d2表示，区域边界变形的幅度由σ1～σ8表示。

根据Maxwell方程，双侧鳍线中电场E与磁场H应满足以下矢量微分方程：

(1)

式中ε0，μ0，εr，μr分别表示真空的介电常数、真空的磁导率、填充介质的相对介电常数和填充介质的相对磁导率。对双侧鳍线主模截止波长、单模带宽和电场结构的计算，需要建立基于磁场为工作变量的泛函矢量公式。由式(1)可以得到基于磁场H的矢量Helmholtz方程为：

(2)

(3)

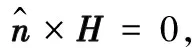
(4)

式中，Γ1和Γ2分别代表导电壁和导磁壁。在计算过程中，实际波导的边界只有导电壁Γ1，故磁场满足的边界条件为式(3)。经过详细理论推导，上述问题等效于如下变分问题(要求εr和μr为实数)：

δF(H)=0，

(5)

式中，

(6)

由矢量有限元离散可以得到矩阵特征值方程：

(7)

式中，各矩阵元素分别为：

(8)

(9)

(10)

(11)

(12)

(13)

对模型进行整体标记可得：

(14)

使用里兹方法进行变分，可得如下方程：

(15)

合成可得特征值方程：

(16)

式(16)即为计算双侧鳍线传输特性的矢量有限元公式。在计算过程中，给出β的取值，就可以求解这个方程，从而得到相应的特征值。具体为可通过求解的最小非负特征值得到主模归一化截止波长特性，将最小非负特征值和第二最小非负特征值做比便可求出单模带宽特性，最后根据各个特征值所对应的特征向量可以得到各个模次的电场结构分布图。

2 结果和分析

2.1 方法验证

为了验证本文推导的基于磁场为工作变量的矢量有限元公式的正确性和有效性，首先使用该方法计算了单侧鳍线的主模归一化截止波长，计算时假设单侧鳍线的尺寸为b/a=0.5，d/b=0.25，t/a=0.01，计算结果如表1所示。由表1可以看出，其相对误差均在2%之内，说明本文所推导的方法是可行的。

表1 单侧鳍线模型的计算结果对照

利用上述方法计算变形对双侧鳍线主模归一化截止波长、单模带宽和场结构的影响。在计算过程中，假设εr=2.55，b/a=0.5，填充的介质区域位于模型最中间，s/a=0.3，d1/a=0.25，d2/a=0.05，t1/a=0.01，t2/a=0.05，双侧鳍线横截面几何变形幅度由σ1/a，σ2/a，σ3/a，σ4/a，σ5/a，σ6/a，σ7/a，σ8/a表示，其变形范围设定为0.01～0.05。

2.2 变形对双侧鳍线主模归一化截止波长和单模带宽的影响计算

通过计算，双侧鳍线不变形时，其主模归一化截止波长和单模带宽值分别为3.108 9和1.893 9。双侧鳍线在使用过程中，可能出现σ1/a，σ2/a，σ3/a，σ4/a，σ5/a，σ6/a，σ7/a，σ8/a中的任意一个或者任意几个变形，限于篇幅，本文着重计算了上述8个中的任意一个、任意2个及任意7个和8个同时出现变形对双侧鳍线主模归一化截止波长和单模带宽的影响，其他变化情况可以仿照计算。主模归一化截止波长和单模带宽随任意一个σi/a变化而引起的变化趋势如图2所示，随任意2个σi/a变化而引起的变化趋势如图3所示，随任意7个和8个σi/a变化而引起的变化趋势分别如图4和图5所示。

(a) 主模归一化截止波长变化规律

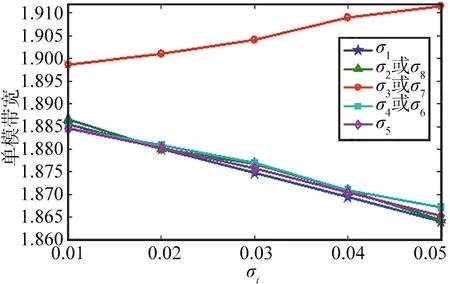
(b) 单模带宽变化规律

(a) 主模归一化截止波长变化规律

(b) 单模带宽变化规律

(a) 主模归一化截止波长变化规律

(a) 主模归一化截止波长变化规律

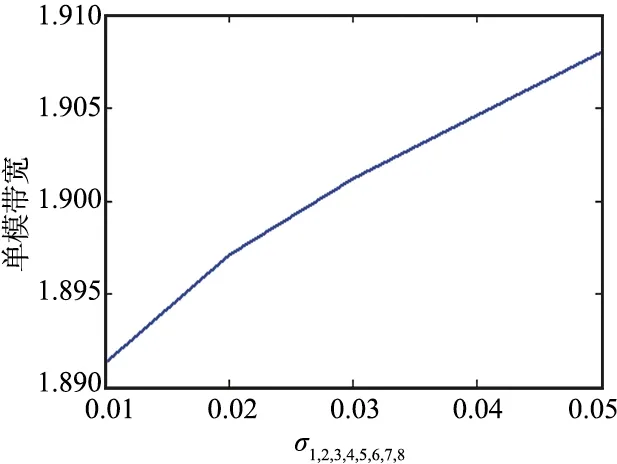
(b) 单模带宽变化规律

2.3 变形对双侧鳍线电场结构的影响计算

本节主要计算双侧鳍线主模、第1高次模、第2高次模和第3高次模的电场结构随σ1/a，σ2/a，σ3/a，σ4/a，σ5/a，σ6/a，σ7/a，σ8/a中的任意3个改变和8个同时改变而引起的改变，如图6和图7所示。为叙述方便和避免重复，每一行4个图形分别对应主模场结构、第1高次模场结构、第2高次模场结构和第3高次模场结构。

(a) 未变形双侧鳍线

(b) 变形双侧鳍线σ2/a=σ3/a=σ4/a=0.05

(c) 变形双侧鳍线σ3/a=σ4/a=σ5/a=0.05

(d) 变形双侧鳍线σ6/a=σ7/a=σ8/a=0.05图6 双侧鳍线的4种模式电场结构随相邻3个σi/a变化而引起的变化情况Fig.6 The variation of field patterns of four modes in bilateral finline with the change of three adjacent σi/a

图7 双侧鳍线的4种模式电场结构随8个σi/a变化而引起的变化情况(σ1/a=σ2/a=σ3/a=σ4/a=σ5/a=σ6/a=σ7/a=σ8/a=0.05)Fig.7 The variation of field patterns of four modes in bilateral finline with the change of eight σi/a

3 结束语

通过分析，可以得出变形对双侧鳍线的主模归一化截止波长、单模带宽和4种模式场结构影响的以下结论：

① 相比于不变形，当变形出现在真空区域边界时，其主模归一化截止波长和单模带宽均减小；而变形出现在加载区域的边界时，其主模归一化截止波长和单模带宽均增加；

② 绝大多数情形的主模归一化截止波长和单模带宽随σi/a的增大呈减小趋势；但也有例外情形，详细为：主模归一化截止波长和单模带宽随σ3/a(或σ7/a)增大而增大；主模归一化截止波长随σ3,7/a增大而增大，单模带宽随σ2,3/a,σ3,4/a(或σ6,7/a)的增大变化不大；当7个σi/a增大时，主模归一化截止波长均减小，而单模带宽随σ1,2,3,4,5,6,8/a(或σ1,2,4,5,6,7,8/a)增大而减小，其余情形随变形幅度增大而增大；

③ 分析上述例外情形，均包含了加载区域的变形(σ3/a，σ7/a)，说明加载区域的变形对双侧鳍线的主模归一化截止波长和单模带宽的影响较大;

④ 双侧鳍线变形后，4种模式的电场线在变形弧度较大区域出现较为集中的现象；

⑤ 相对于真空区域，介质加载区域的变形对电场结构的影响更大，尤其是对第1高次模和第2高次模的影响；

⑥σ1/a,σ5/a的变化对4种模式场结构的影响较小；

⑦ 未发生变形模型区域，4种模式电场结构整体上与整体模型不变形时大致一样，说明场结构变化主要集中在变形区域附近；

⑧ 8个模型边界均发生变形，双侧鳍线4种模式场结构与未变形时整体分布相似。

综上，本文推导的矢量有限元计算公式可以进一步丰富和完善非均匀传输线传输特性的计算方法，对变形双侧鳍线传输特性的计算结果和结论可作为鳍线在新型微波和毫米波器件中使用时的一些参考。