张拉整体伸展臂的构建方法研究
罗阿妮,张晨阳,杨建龙,邹云涛,刘贺平
(1.哈尔滨工程大学 机电学院,哈尔滨 150001;2.潍柴动力股份有限公司,潍坊 261061;3.中车长春轨道客车股份有限公司,长春 130062)
0 前言
空间伸展臂,既可以为航天器提供支撑,也可以为航天器提供展开动力,因此空间伸展臂的研究对未来的航天发展具有重要意义[1-2]。铰接式伸展臂具有展开刚度大,重复展开精度高等特点,是目前使用最多的可展结构[3]。但是此类伸展臂的铰链结构复杂,设计难度大,且复杂的铰链结构也导致了伸展臂的质量大幅增加,因此铰链的设计一直是此类伸展臂设计的重点,其设计难度也限制了其发展。张拉整体结构是一种由杆构件和索构件组成的结构,索网由杆构件在内部撑出预期形状,且杆构件相互不接触[4]。正是由于张拉整体中杆构件都不相互接触,当把其转化为可展结构时,就省却了设计复杂刚性铰链的麻烦,也避免了传统刚性铰链在运动范围方面的限制。张拉整体结构的构件都只承受轴向力,所受外载都会由所有构件来承担,结构整体的材料利用率高,质量小[5]。正是由于张拉整体结构的这些优点,近些年来,许多研究人员都在尝试把臂状张拉整体结构转化为伸展臂[6]。
Gunnar[7]基于臂状张拉整体结构,构建了一种伸展臂。此伸展臂的杆构件能够实现弹性弯曲变形,通过拉紧索来保持杆构件的弯曲和整体的折叠。当拉紧的索构件被释放时,杆构件在弹力作用下伸直,从内部支撑索网结构,形成预期的臂状张拉整体结构。Veuve等[8-10]研究了二阶臂状张拉整体结构的可折展方法。此可展结构的杆构件都为刚性构件,不可折叠,而部分索构件串联以驱动机构折展,另一部分索构件用弹簧替代。由于相连的杆构件之间相对运动较为复杂,因此杆构件的连接采用球副或万向节。Averseng等[11]把多个四杆张拉整体单元侧面拼接,形成一个臂状张拉整体结构。把张拉整体单元的斜索作为驱动索,通过驱动索的缩短,驱动折叠状态的臂状结构展成预定状态。李冰玉等[12]基于张拉整体结构,建立连续型机械臂力学模型,并对其准静态和动态进行分析,最后通过实验平台验证模型的准确性,并进一步分析机械臂在空间工作时的奇异姿位。Fadeyev等[13]搭建了两级张拉整体机械臂实验平台,该平台周围设有8个OptiTrack摄像机,通过光学运动捕捉节点的位移信息。该实验平台使张拉整体机械臂样机的实验数据与理论分析得到有力的验证,该实验平台也适用于其他张拉整体研究的信息捕捉。
张拉整体结构中,杆构件支撑索网形成预期形状,杆构件对整体刚度起到决定作用。二阶张拉整体结构中存在运动副,增加了设计的难度和结构的复杂程度。侧面拼接的张拉整体结构的力学特性较轴向拼接的张拉整体结构差。因此,本文将基于张拉整体单元轴向拼接形成的臂状张拉整体结构,研究一种新型的张拉整体伸展臂的构建方法。
1 臂状张拉整体结构的数学模型
张拉整体伸展臂是由臂状张拉整体结构转化而成的,因此应首先构建臂状张拉整体结构。下面将研究基于节点矩阵和连接矩阵的臂状张拉整体结构的通用构型方法。
1.1 节点矩阵
多个张拉整体单元,沿其轴向进行拼接,就可以形成臂状张拉整体结构[14],图1所示为3杆张拉整体单元轴向拼接形成的臂状张拉整体结构。拼接所用的张拉整体单元除了单元内扭转角,其他结构参数都相同,且相邻单元的单元内扭转角之和为360°。臂状张拉整体结构的构件可以分成5类,如图1所示,杆(1)、斜索(2)、附加索(3)、鞍索(4)、端面水平索(5)。

图1 臂状张拉整体结构Fig.1 Tensegrity arm
组成臂状张拉整体结构的张拉整体单元由下至上排序,奇数层单元的节点坐标可表示为
(1)
(2)
式中,j为组成臂状张拉整体结构单元序号且为奇数,Ndij为第j层单元下端面第i个节点,Nuij为第j层单元上端面第i个节点,r为单元端面外接圆半径,h为单元高度,η为相邻单元的重合高度hη和h的比值,ɑ为单元内转角,β为相邻单元间转角。
偶数层单元的节点坐标可表示为
(3)
(4)
由下至上对单元进行排序,将各单元的节点坐标按顺序放入一个矩阵,就形成了节点矩阵
N=[Nd11…Nu11…Nd1q…Nu3q]
式中,q为此臂状张拉整体结构的层数。
1.2 杆矩阵
此臂状张拉整体结构的杆矩阵可以表示为
B=[B1B2…Bj…B3q]=N·CB
(5)
式中,Bj(j=1,2,…,3q)为第j根杆对应的杆向量,此向量为列向量,CB为杆连接矩阵,且
I3∈R3×3是单位阵,O∈R3×3是零矩阵[15]。
1.3 索矩阵
此臂状张拉整体结构的索矩阵可以表示为
S=[S1S2S3S4]
(6)
式中,S1,S2,S3,S4分别为鞍索矩阵、斜索矩阵、附加索矩阵和水平索矩阵。
1) 鞍索矩阵
鞍索位于相邻单元结构的交叉部位,其两端连接的杆构件属于不同的单元,所有鞍索列向量组成的鞍索矩阵可表示为
S1=N·CS1
(7)
其中,CS1为鞍索连接矩阵,
CS1=[E1E2]∈R6q×6(q-1)
(8)
2) 斜索矩阵
结构中所有斜索列向量组成的斜索连接矩阵可写作
斜索矩阵可以表示为
S2=N·CS2
(9)
3) 附加索矩阵
表示所有附加索与节点连接关系的附加索连接矩阵为
CS3=[E3E4]
(10)
式中,
附加索矩阵可写成
S3=N·CS3
(11)
4)水平索矩阵
反应所有水平索和节点连接关系的水平索连接矩阵可表示为
(12)
式中,矩阵O1∈R3×3和O2∈R3×6(q-1)都是零矩阵,
水平索矩阵可写作
S4=N·CS4
(13)
这样,给定q、r、h、η、ɑ、β,就可以获得任意层数的3杆臂状张拉整体结构的节点矩阵和构件连接矩阵,进一步计算可以获得构件向量和结构数学模型,这样就形成了3杆臂状张拉整体结构的自动构型方法。令r为145 mm,h为200 mm,η为1/3,α=120°,β=60°,q=4,所形成的4层3杆臂状张拉整体结构简图如图1所示。此结构中,同类构件的长度相同,杆长为312.1 mm,水平索长为200 mm,附加索长为197 mm,斜索长为251.1 mm,鞍索长为159.6 mm,结构整体的对称性好。
2 臂状张拉整体结构受力变形分析
2.1 受力变形理论分析
图1所示的状态为臂状张拉整体结构的展开状态。当把臂状张拉整体结构转化为伸展臂结构时,其预期的折叠状态为结构沿轴向折叠,其高度大幅度减小,从而使得伸展臂折叠状态体积减小。而且,折叠与展开的过程基本是可逆的,因此可以通过臂状张拉整体结构折叠来确定其转化为伸展臂的方案。
在臂状张拉整体结构两端施加轴向压力,可以促使此结构轴向长度减小,达到其轴向折叠的效果。因此,下面将对结构整体施加轴向压力,分析其构件的变形和受力,从而确定驱动构件和随动构件的选择方案,为臂状结构转化为伸展臂提供依据。
分析臂状张拉整体结构的受力变形时,结构端面受力如图1所示,即在上下端面节点处添加方向相反的轴向压力,从而实现对结构整体的压缩。受力变形分析,最为直接的就是利用表示受力与变形间关系的刚度矩阵,求取给定外载下的节点位移,从而获得构件的长度变化。
空间结构的受力变形关系可表示为
W=Kδ
(14)
式中,W为结构节点所受的外载向量,K为结构的刚度矩阵,δ为结构的节点位移向量。因此
δ=K-1W
(15)
张拉整体的结构刚度矩阵K由两部分组成,即
K=Ke+Kg
(16)
其中,Ke为弹性刚度矩阵,Kg为几何刚度矩阵[16]。
变形后的节点坐标可表示为
NV1=NV+δ
(17)
式中,NV为N转化成的列向量。
几何刚度矩阵Kg是利用构件的预紧力构建的,因此,需要求取结构在初始状态的预紧力。求解构件预紧力的方法很多,最为常用的是利用平衡方程进行求解。初始状态下,结构不受外力,其处于自平衡状态,此时结构的平衡方程可表示为
AT=0
(18)
其中,A为结构的平衡矩阵,T为构件内力向量。
利用SVD法对平衡矩阵A进行分析[17],可得
A=UλV
(19)
其中,矩阵λ的对角线元素为矩阵A的特征值,其非零值个数与平衡矩阵的秩相等,U和V的列组成了平衡矩阵正交的基向量,分别为张拉整体结构的位移模态向量和自应力模态向量。
当此结构的自应力模态数为c(即矩阵A的列数与其秩的差值)时,矩阵V的右侧c列向量组成了此平衡方程的零空间正交基VNull,即:
VNull={v1v2…vs}
(20)
根据式(20),那么构件的初始预紧力T0可以表示为
T0=VNull·C
(21)
C=[c1c2…cs]T
(22)
式中,C为零空间正交基底的组合系数向量,其元素可以为任意实数。
2.2 驱动构件的确定
根据2.1节的理论,下面进行4层3杆臂状张拉整体结构的受力变形分析。这里,杆构件和索构件的材料都为钢,杆构件截面直径为10 mm,索构件的截面直径为1 mm,其他结构尺寸的设置与1.3节相同。此结构的重力为24.2 N,通过SVD法分解平衡矩阵,获得构件预紧力之间的比例关系。令杆构件的预紧力为50 N,此时斜索预紧力为34.1 N,附加索预紧力为44.7 N,鞍索预紧力为52.9 N,水平索预紧力为16.9 N,这样,构件预紧力与结构重力为相同量级,重力引起的结构变形较小。
结构上下端面节点施加的轴向力由0 N变化到45 N,图2显示了臂状张拉整体结构受力变形前后的状态图。由2图可知,结构受压后,其高度和半径都会有所变化。图3为外力与结构整体高度和端面直径的关系曲线。图3中,当外载为0时,端面直径近似不变,而整体高度降低了约2 mm,即结构自身重力引起的自身结构变形较小,这说明预紧力的设置是合理的。随着外力的增加,结构整体高度减小,端面直径增加,而且,端面直径的变化量比整体高度的变化量要小一个数量级,也就是结构整体外包络体积的变化主要受结构高度的影响,这也证明了此臂状张拉整体结构非常适合于将其转化为空间可展结构。

图2 臂状张拉整体结构的变形Fig.2 Deformation of tensegrity arm
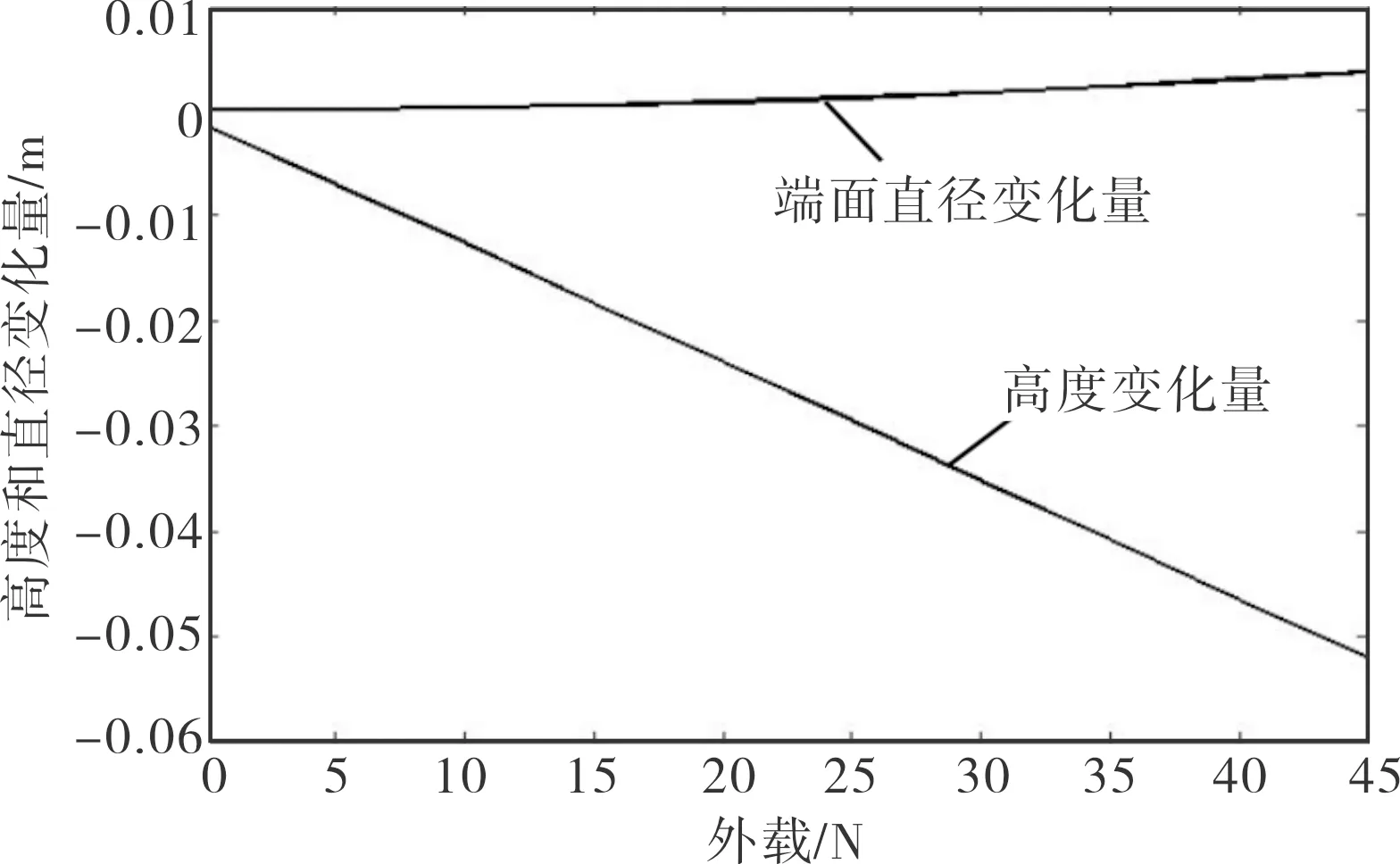
图3 高度和端面直径的增量曲线Fig.3 Incremental curves for height and end face diameter
图4为各类构件的长度与外载的关系曲线。由图4可知,随着外力的增加,附加索和斜索的长度减小,鞍索的长度增加,水平索的长度基本不变。与附加索和斜索的长度减少量相比,鞍索长度的增加幅度要小得多。附加索在长度变化上大于斜索,这说明附加索在结构高度减少的过程中,反应更加敏感,即利用附加索驱动伸展臂更为适宜。

图4 构件长度变化曲线Fig.4 Curves for members length
3 索构件弹性化方案
3.1 方案制定
通过结构受力变形分析可知,在臂状张拉整体结构压缩过程中,附加索、斜索和鞍索都出现了明显的长度变化,而水平索的长度变化量较其他索构件小得多,因此这里水平索依然选用弹性小的索构件。在折叠过程中,附加索和斜索的长度都是减小的,两者都可以作为驱动结构折叠的驱动构件。由于此结构的附加索处于竖直状态,且都分布于几条竖直线上,易于串连,且长度变化量较大,因此这里选择附加索为驱动构件。在此基础上,一部分索构件长度也需要随着结构的折展有明显的变化,这里将采用弹簧替代这些需要长度变化的索构件。根据2.2节的分析,这里提出了3种索构件用弹簧替代的方案:
1)除水平索件,其他索构件皆用弹簧来代替,即18根斜索和18根鞍形索用弹簧替代。
2)只有18根鞍索用弹簧替代。
3)只有12根鞍索用弹簧替代。
3.2 方案分析
1)方案1
根据图1所示构件的几何关系分析,采用弹性化方案1的臂状张拉整体结构的中间一层的折叠过程大体如图5所示。由图5可知,此结构能在附加索的驱动下实现整体沿其轴线的折叠,在忽略构件直径的情况下,此结构最终将折叠到一平面。此结构在完成折叠后,其鞍索构件在底面上的投影围成了一个正六边形,杆构件的投影在内部围成正三角形。设lb为杆长,此正六边形的外接圆半径为:

图5 方案1的折叠过程Fig.5 Deployment for scheme 1
正六边形边长
鞍索原长为120.19 mm,杆长为264.575 mm。折叠后,鞍索长度为152.80 mm,鞍索伸长量为Δla=32.61 mm。
2)方案2
采用弹性化方案2的结构折叠过程与折叠后的形状和方案1类似,折叠后的结构依然呈一正六边形,构件长度的变化也和方案1相同。
3)方案3
采用弹性化方案3的臂状张拉整体结构在附加索驱动下的折叠过程和方案1也相同,折叠完成后,整体结构也将折叠到一个平面,其折叠后的构件在底面上的投影如图6所示。方案3的鞍型索柔性化数量减少了一半,每个中间层的鞍索有6根,这里只把其中3根弹性化。因为未弹性化的鞍索在折叠时长度不变,弹性化的鞍索将被伸长,当此臂状结构被压缩到底面时,其同一层的鞍索围成一个六边形,此六边形不是正多边形,其杆构件依旧围成正三角形。图6所示的六边形行中,短边长为120.19 mm,长边长为183.14 mm,弹性化的鞍索伸长量为Δla=62.95 mm。
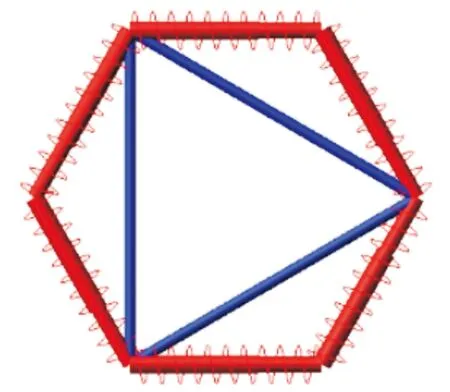
图6 方案3单元折叠俯视图Fig.6 Top view of unit deployment for scheme 3
3.3 方案确定
用弹簧替代索的数量越多,结构的刚度越低,影响伸展臂的承载能力。且弹簧的伸长量越大,需要其刚度越低,这也将影响整个结构刚度。综合对比3个方案,方案1中,弹簧的伸长量小,但数量过多;采用方案3的结构中,弹性化的构件数量少但弹簧的伸长量大;相比于前两种方案,方案2在弹性化构件数量和弹簧伸长量方面具有绝对优势。
根据这3个方案,分别在动力学软件中建立张拉整体伸展臂的仿真模型(图7),进行折叠可行性的分析。仿真模型的结构尺寸与受力变形分析时的设置相同。这里,所有索构件都用弹簧来表示,弹性化的索构件的弹性系数设置为2 N/mm,未弹性化的索构件的弹性系数设置为200 N/mm。通过仿真分析发现,只有采用弹性化方案1的张拉整体伸展臂能够在附加索驱动下折叠到高度最小,而采用其余两个弹性化方案的伸展臂都会出现在折叠过程中机构卡死导致其无法折叠到高度最小的现象。因此,这里选择方案1作为索构件弹性化方案。

图7 张拉整体伸展臂仿真模型Fig.7 Simulation model of tensegrity extension arm
4 折展过程的仿真分析
图8为根据弹性化方案1设置的张拉整体伸展臂在附加索驱动下的折叠过程,此折叠过程用10 s完成。折叠完成后,机构将保持折叠状态5 s,再由弹簧和附加索配合驱动此伸展臂展开,展开过程用时10 s。

图8 仿真模型的折叠过程Fig.8 Deployment of the simulation model
图9为折展过程中机构外包络圆柱的高度和端面直径的变化。由图9可知,机构折叠状态的高度为83 mm,端面直径为331 mm,展开和折叠状态的外包络圆柱体积比为5.55,高度比为7.23,端面直径比为0.88。由仿真可知,张拉整体伸展臂能够在附加索的驱动下完成折叠和展开,分析获得的驱动方案和弹性化方案是可行的。而且,与高度变化相比,端面直径的变化要小得多,整体结构的外包络体积也是主要受结构高度的影响,这与2.2节的结论相同,进一步证明了此臂状张拉整体结构适合于转化为伸展臂结构。
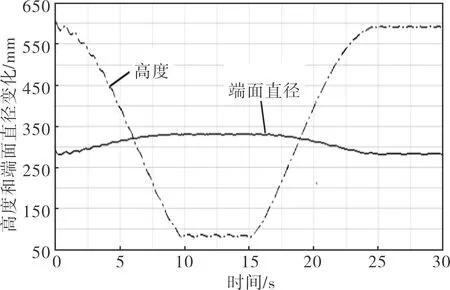
图9 折展过程中机构外包络圆柱的高度和端面直径的变化Fig.9 Changes of the height and end face diameter of the outside enveloping cylinder of the mechanism during deployment
图10显示了此伸展臂运动过程中构件长度的变化。鞍索的长度最大变化量为48.5 mm,约占其初始长度的1/3;斜索长度最大变化量为11.4 mm,约占初始长度的5%;水平索的长度变化量很小,可忽略;附加索长度变化量最大值为100 mm,超过其初始长度的50%。与附加索相比,弹性化的鞍索和斜索长度变化量小,选择相应的替代弹簧较容易,而水平索的长度变化量也证明了未将其弹性化的正确性。

图10 折展过程中构件长度的变化Fig.10 Change of members length during deployment
5 实验研究
根据前面的分析,获得了臂状张拉整体结构转化为张拉整体伸展臂的具体方案,并通过仿真分析,对方案的可行性进行了验证。根据这一方案,搭建张拉整体伸展臂模型(如图11(a)所示)。图11(a)~11(d)显示了此张拉整体伸展臂在附加索的驱动下,折叠状态运动到展开状态运动的过程。这一过程主要是在弹簧驱动下完成的,而附加索随动释放,起到控制整个伸展臂展开速度的作用。此时,附加索串联形成3根从顶部连到底部的驱动索,只需要3个电机来分别控制其长度变化。当附加索协同缩短,此机构会由展开状态(图11(d))折叠到图11(a)所示状态,其过程与展开过程正好相反。这说明此张拉整体伸展臂能够在附加索的驱动下实现展开和折叠,此伸展臂方案是可行的。

图11 张拉整体伸展臂的折叠过程Fig.11 Deployment of the tensegrity extension arm
在实验过程中也发现,当附加索的缩短或伸长速度有所偏差时,此张拉整体伸展臂在运动过程的形状会有所偏差,但是当运动结束,所有附加索的伸长或缩短量都达到设定值时,此伸展臂的最终状态是相同的。这也说明了此机构运动对控制精度要求不高,易于控制。在构件尺寸发生改变或者受到外力作用时,张拉整体结构能够通过形状改变来达到新的平衡状态,正是由于其这种特点,在张拉整体机构运动过程中,即使驱动有所偏差,机构也能够在构件内力共同作用下,达到新的平衡状态,这正是运动过程中机构形态有所偏差的原因。
6 结论
本文从臂状张拉整体结构数学模型的建立、臂状张拉整体结构的受力分析、驱动方案和索构件弹性化方案分析、仿真分析和实验研究几个方面,分析了臂状张拉整体结构转化为张拉整体伸展臂的方法,并对获得的机构方案的可行性进行了仿真和实验验证。通过本文的分析,获得如下结论:
1)张拉整体伸展臂能够在附加索和弹性化的斜索与鞍索驱动下实现折展;
2)附加索可以串联,从而减少驱动构件个数,降低控制难度;
3)张拉整体伸展臂折展状态的高度变化量,要比其截面直径变化量大很多,即结构的外包络体积主要受其结构高度影响;
4)张拉整体伸展臂折展状态的高度和外包络体积的变化都很大,说明了臂状张拉整体结构适宜于转化为伸展臂结构;
5)本文通过臂状张拉整体结构的折叠分析,获得了驱动此结构展开的设计方案,分析方法的可行性也通过仿真和模型实验得到证实。

