基于随机森林的系统性能指标贡献率评估

刘金灿　田星　周红彬　尹波

【摘要】    针对系统性能评估结果，分析各类指标在本次评估中的贡献率，是系统实现有针对性优化改进的重要基础。基于随机森林算法中的变量重要性测量（Variable Importance Measure，VIM），面向指标体系与评估结果值构建随机森林模型，设计实现一种系统性能指标贡献率评估方法，完成系统性能评价中指标重要程度排序。仿真结果表明，该方法可以精准快速地选取对系统评估结果影响较大的指标，从而为系统性能的提升提供理论支撑。

【关键词】    性能评估    随机森林    变量重要性测量    指标贡献率    机器学习

引言：

近年来，面向系统性能评估的研究主要集中在评估算法的优化改进及实现[1]，针对性能评估结果的进一步分析，以及判断评估指标对系统性能评价的贡献程度，在国内外尚未开展专门研究。关于体系贡献率、节点重要性分析的相关研究，目前主要集中在装备体系贡献率评估[2-7]，以及复杂网络节点重要性计算[8-11]中;文献[12]基于灰靶理论实现指挥信息系统指标体系贡献度计算，但未与系统性能评估相关联;文献[13]提出了一种基于随机森林的重要性测度分析方法，从而找出重要特征变量，降低输入空间的维数，节约运算成本。然而，均未从系统性能评估的角度，开展指标贡献率分析，无法支撑系统顶层完成“系统设计-性能评估-指标贡献率分析-系统性能优化”的闭环。

随着机器学习领域相关研究的不断深入，关于随机森林算法的优化与应用迅猛发展。自Breiman于2001年提出以来[14]，该算法凭借其在特征选择、分类识别上的独特优势，已广泛应用于生态学、医学、天文学、农业等行业。本文提出的系统性能指标贡献率方法，利用随机森林算法在决策树构建过程中变量重要性测量（Variable Importance Measure ，VIM），完成指标重要程度的识别，具有良好效果。

一、系统性能指标贡献率评估方法

“贡献率”一词多出现于经济领域，用以表示某一经济形式对整体经济增长的作用程度。本文借用该词表征在系统性能评估中，参与评估计算的各类指标，对系统综合效能评价的影响程度。指标贡献率越高，表明该指标对系统性能评估结果影响越大，从而可有针对性地进行系统性能提升。

（一）随机森林算法与适用性分析

随机森林算法是经典的数据挖掘算法之一，其核心在于决策树的构建，并通过多颗决策树的组合，完成对样本数据的特征识别与提取，提高分类的准确性。

决策树采用树形结构，从根节点出发自顶向下递归构建。在构建过程中，按照一定的规则，对样本数据进行特征提取与逐层分类，即将样本数据依次放入下一层的“左”或“右”子节点中，形成树的“分裂”。当完成所有决策树的构建后，每棵树最底层的树节点共同完成所有样本数据的分类。

随机森林算法在实现过程中的关注点包含两个方面：一是单棵决策树生成的正确率，也称为单棵决策树的强度，即每次树节点分裂的正确性，多颗决策树的强度综合决定了整体森林的分类性能;二是降低每颗决策树之间的相关性，从而“独立”地为最终分类结果负责，提高整体森林的可信度。

面向系统性能指标的贡献率评估，可以归纳为指标体系（输入变量X）对评估结果（输出变量Y）影响程度的问题。其中，针对复杂系统的性能评估，其指标体系复杂、指标数量多，同时指标数据的变动具有非线性特征，且为多类指标共同作用下决定评估结果值的大小。也就是说，输入变量不确定性较强、呈非线性关系，且多类变量存在相互交叉、共同作用的关系。

随机森林通过构建一系列决策树来解决样本数据高维度处理难题，而决策树模型本身属于非线性分类（回归）模型，最终分类结果通过每棵树的结果进行投票获得，而不依赖于特定的输入数据（单棵决策树），特别适合解决交叉作用显著的問题。另外，随机森林算法通过统计学习可以自动识别出对输出变量影响较大的输入变量。因此，该算法在解决指标贡献率评估上具有较强的适用性。

（二）基于随机森林的指标贡献率评估

将随机森林算法应用于指标贡献率评估，首先假设指标体系共包含n个子指标X，X，...，X，且改变指标数据后，进行N次性能评估，将产生的评估结果记为Y，Y，...，Y，并将所有变量（包括输入变量X与输出变量Y）组成的样本数据集合记为T。则基于随机森林的指标贡献率评估方法，分为以下两步实现：

1.随机森林模型构建，即决策树的构建

从总样本数据T中随机抽样组成m个训练子集，并将第k个训练子集记为T，其数据规模大小记为N，则有：

对任意的T，分裂形成单棵决策树，最终m个训练子集将形成m个决策树，并共同构成随机森林。

其中，决策树个数m的选择由样本数量多少决定：若样本数量充足，m越大，则表明单棵决策树对最终结果影响越小，一定程度上可避免个别差错数据对整体结果的影响，而m过大又会带来算法时间和空间上的开销;若样本数据有限，则可以适当减少决策树的个数，避免出现不同决策树使用相同数据集的情况，或者通过数据随机扰动的方式，扩大样本规模。

2.指标贡献率计算

在每棵决策树生成的过程中，基于节点的不确定性下降量，计算产生该颗决策树的变量重要性测量（VIM）;当随机森林模型构建完毕后，进一步计算得出m个决策树的平均重要性测量结果（PVIM），最终为各指标计算得到贡献率评分值。

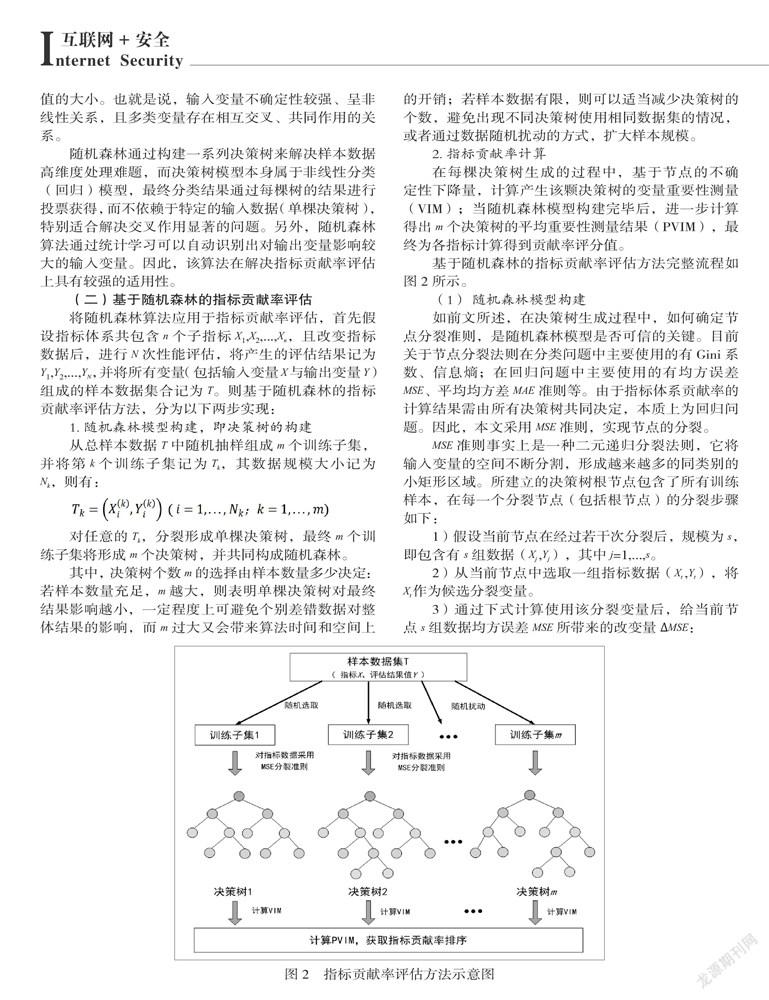
基于随机森林的指标贡献率评估方法完整流程如图2所示。

（1） 随机森林模型构建

如前文所述，在决策树生成过程中，如何确定节点分裂准则，是随机森林模型是否可信的关键。目前关于节点分裂法则在分类问题中主要使用的有Gini系数、信息熵;在回归问题中主要使用的有均方误差MSE、平均均方差MAE准则等。由于指标体系贡献率的计算结果需由所有决策树共同决定，本质上为回归问题。因此，本文采用MSE准则，实现节点的分裂。

MSE准则事实上是一种二元递归分裂法则，它将输入变量的空间不断分割，形成越来越多的同类别的小矩形区域。所建立的决策树根节点包含了所有训练样本，在每一个分裂节点（包括根节点）的分裂步骤如下：

1）假设当前节点在经过若干次分裂后，规模为s，即包含有s组数据（X ，Y），其中j=1，...，s。

2）从当前节点中选取一组指标数据（X，Y），将X 作为候选分裂变量。

3）通过下式计算使用该分裂变量后，给当前节点s组数据均方误差MSE所带来的改变量ΔMSE：

ΔMSE=MSE -P*MSE-Pl*MSE

其中， MSEf表示父节点的MSE值，MSEr、MSEl分别表示分裂后的右节点与左节点的MSE值，Pr和Pl分别表示父节点落入孩子右节点与孩子左节点的概率（右/左节点数据量与父节点数据量之比）。均方差MSE是利用组内评估值Yj计算得到，以当前含有s组数据的节点为例，公式如下：

其中，t=1，...，s;为根据袋外数据（Out Of Bag， OOB）重新评估得到的预测值。

4）将该节点s组数据全部轮循作为候选分裂变量后，将ΔMSE最大的一组值的X作为分裂阈值。父节点中的指标数据小于该阈值的样本分配到左子节点中，剩余的样本分配至右子节点中，从而完成一次节点分裂。

按照上述步骤，对每个节点依次进行逐层的分裂，直至达到分裂停止条件。停止条件主要为达到了预设的决策树高度值，该值的设置避免了持续分裂使该节点VIM为0的情况，防止数据出现过拟合现象。

当节点分裂完毕后即形成一棵决策树，m个决策树生成后，共同组成随机森林模型，具体实现流程如图3所示。

（2）指标贡献率计算

在随机森林模型的构建过程中，利用决策树节点的ΔMSE进行分裂，也就是说该节点处的MSE值直接决定了每颗决策树的分裂结构与随机森林模型的最终样式。因此，可以将该节点处的MSE值作为不确定性下降量，从而进一步求取决策树的变量重要性测量值以及随机森林的平均重要性测量值。指标贡献率的计算步骤如下：

1）计算某颗决策树中某个节点的不确定性下降量，计算公式为MSE *N-MSE *N-MSE *N。其中，MSE 表示当前节点的MSE值，MSE、MSE分别表示右子节点与左子节点的MSE值，N、N、N分别是当前节点、右子节点、左子节点的样本数量。

2）遍历整棵树中的所有节点，将每个节点的不确定性下降值进行累计求和、取平均处理，得到单棵决策树的变量重要性测量值（VIM），并对所有VIM进行归一化处理。

3）基于单棵决策树的VIM结果，对随机森林所有决策树求取变量的平均重要性测量值（PVIM），并作为最终结果。

按照指标PVIM计算值的大小，即可实现对指标重要程度的排序，完成指标贡献率评估。

二、指标贡献率评估方法应用仿真

为检验本文提出的基于随机森林的指标贡献率评估方法，面向卫星通信网络系统，运用该方法构建随机森林模型，并实现指标贡献率评估分析，以测试其可行性与有效性。

（一） 指标体系与评估结果

以卫星通信系统的通信组网场景为例，首先为该场景设置评估指标体系，如图4所示。

针对系统的通信组网场景，重点关注决定用户服务质量的组网能力与通信能力，分别将两种能力指标具化后，形成2层7个子指标，包括网络吞吐量、资源利用率、切换时间、切换成功率、业务流量、业务时延、业务丢包率。为获取足够多的样本数据量，为子指标设置200组不同的数据值。

另外，为进一步验证本文所提方法的合理性，采用具有主观因素的层次分析法，对每组指标数据值，进行系统性能评估。部分归一化后的指标数据与对应的评估结果见表1。

在层次分析法的评估过程中，网络吞吐量、资源利用率、切换时间、切换成功率、业务流量、业务时延、业务丢包率7类指标的权重分别为[0.24，0.09，0.18，0.09，0.16，0.12，0.12]。

（二）指标贡献率评估

按照上文所述的指标贡献率评估方法，为指标数据值及对应的评估结果构建500棵决策树组成的随机森林模型。由于参与评估的指标类型较少，将决策树的高度阈值预设为5。

以网络吞吐量指标为例，根据MSE 分裂准则形成的决策树，其单颗决策树下的变量重要性测量值（共500个）经过計算后为：[0.388，0.192，0.240，0.219，0.308，0.282，0.271，…]。而对于随机森林模型来说，该指标的变量平均重要性测量值为0.282。

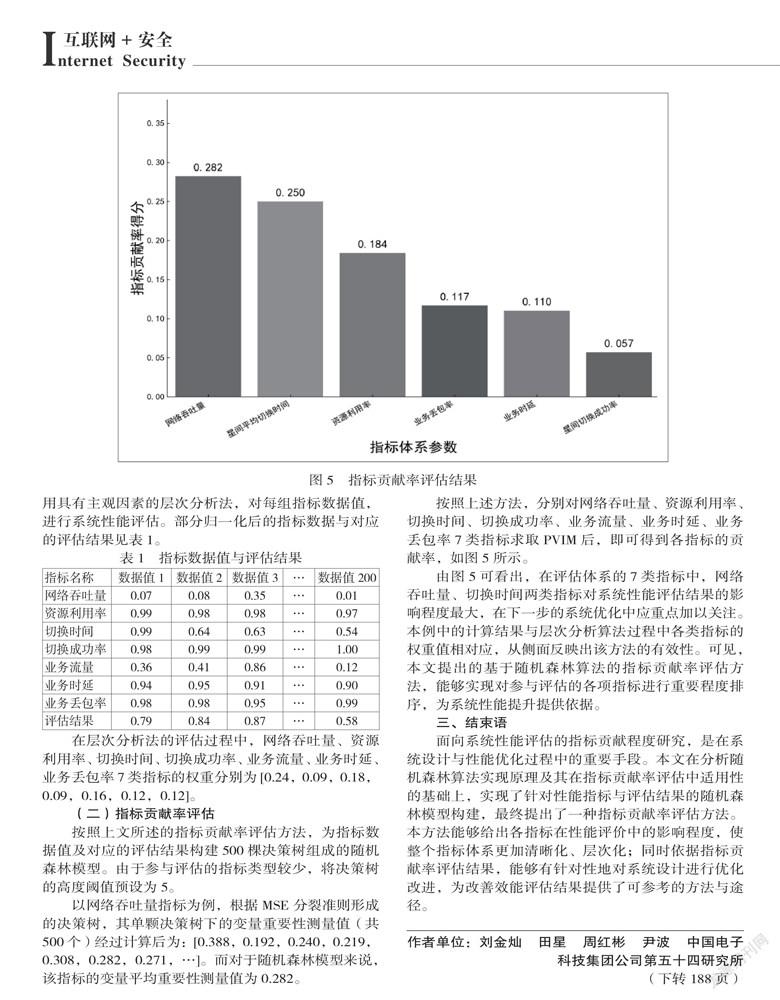
按照上述方法，分别对网络吞吐量、资源利用率、切换时间、切换成功率、业务流量、业务时延、业务丢包率7类指标求取PVIM后，即可得到各指标的贡献率，如图5所示。

由图5可看出，在评估体系的7类指标中，网络吞吐量、切换时间两类指标对系统性能评估结果的影响程度最大，在下一步的系统优化中应重点加以关注。本例中的计算结果与层次分析算法过程中各类指标的权重值相对应，从侧面反映出该方法的有效性。可见，本文提出的基于随机森林算法的指标贡献率评估方法，能够实现对参与评估的各项指标进行重要程度排序，为系统性能提升提供依据。

三、结束语

面向系统性能评估的指标贡献程度研究，是在系统设計与性能优化过程中的重要手段。本文在分析随机森林算法实现原理及其在指标贡献率评估中适用性的基础上，实现了针对性能指标与评估结果的随机森林模型构建，最终提出了一种指标贡献率评估方法。本方法能够给出各指标在性能评价中的影响程度，使整个指标体系更加清晰化、层次化;同时依据指标贡献率评估结果，能够有针对性地对系统设计进行优化改进，为改善效能评估结果提供了可参考的方法与途径。

作者单位：刘金灿    田星    周红彬    尹波    中国电子科技集团公司第五十四研究所

参  考  文  献

[1]马亚龙， 邵秋峰， 孙明， 等. 评估理论和方法及其军事应用[M]. 北京： 国防工业出版社， 2013.

[2]陈立新. 一种通用的装备体系贡献率评估框架[J]. 军事运筹与系统工程.2020， 34（2）： 33-38.

[3]张博孜， 张国忠， 常华耀. 武器装备体系贡献度评估问题研究[J]. 计算机仿真， 2018， 35（2）： 397-401.

[4]罗小明， 朱延雷，何榕.基于复杂网络的武器装备体系贡献度评估分析方法[J]. 火力与指挥控制， 2017， 42（2） ： 83 - 87.

[5]吕惠文， 武庆春， 张炜. 基于灰色证据理论的装备体系贡献率评估[J]. 军事交通学院学报， 2017， 19（5）：22-27.

[6]何舒， 杨克巍， 梁杰.基于网络抗毁性的装备贡献度评价[J]. 火力与指挥控制，2017，42（8） ： 87-91.

[7]赵丹玲，谭跃进，李际超， 等.基于作战环的武器装备体系贡献度评估[J].系统工程与电子技术，2017，39（10） ： 2240-2245.

[8]胡钢， 徐翔， 张维明， 等. 基于主成分分析的网络节点的重要性指标贡献评价[J]. 电子学报， 2019， 47（2）： 358-365.

[9]吴果， 房礼国， 李中. 基于多指标综合的复杂网络节点重要性评估[J]. 计算机工程与设计， 2016， 37（12）： 3146-3150.

[10]张喜平， 李永树， 刘刚， 等. 节点重要度贡献的复杂网络节点重要度评估方法[J]. 复杂系统与复杂性科学， 2014， 11（3）： 26-31.

[11]周漩， 张凤鸣， 李克武， 等. 利用重要度评价矩阵确定复杂网络关键节点[J]. 物理学报， 2012， 61（5）： 1-7.

[12]孙源泽， 赵东杰. 基于灰靶理论的指挥信息系统性能指标贡献度评估方法研究[J]. 指挥与控制学报， 2015， 1（2）：228-231.

[13]宋述芳， 何入洋. 基于随机森林的重要性测度指标体系[J]. 国防科技大学学报， 2021， 43（2）： 25-32.

[14] Breiman L. Random forests[J]. Machine learning， 2001， 45（1）： 5-32.

[15] B Gregorutti， B Michel， P Saint-Pierre. Correlation and variable importance in random forests[J]. Statistics & Computing ， 2017 ， 27 （3） ：659-678.

[16] H Hassan， ABadr， MB Abdelhalim. Prediction of O-glycosylation Sites Using Random Forest and GA-Tuned PSO Technique[J]. Bioinformatics & Biology Insights， 2015， 9（9） ： 103-109.

[17]张马兰， 刘君强， 左洪福， 等. 基于区间数学理论和贝叶斯网络指标灵敏度分析[J]. 武汉理工大学学报（交通科学与工程版）， 2015， 39（1）：162-165.

[18]刘凯. 随机森林自适应特征选择和参数优化算法研究[D]. 长春： 长春工业大学， 2018.

[19]彭漂. 基于随机森林的变量重要性度量和核密度估计算法研究[D]. 厦门： 厦门大学， 2017.

[20]马骊. 随机森林算法的优化改进研究[D]. 广州： 暨南大学， 2016.

[21]张鑫， 吴海涛， 曹雪虹. Hadoop 环境下基于随机森林的特征选择算法[J]. 计算机技术与发展， 2018， 28（7）： 88-92.