基于网络/基站RTK 移动摄影测量数据的垂向精度分析1

丁 锐 李环宇 张世民 姜大伟 刘 睿 李 安

1）中国地震局地质研究所, 北京 100029

2）应急管理部国家自然灾害防治研究院, 北京 100085

3）浙江省地震局, 杭州 310013

引言

研究活动构造在地貌上的表现时需大量的定量化参数，如断裂长度、分段长度、同震位移等（邓起东等，2004；Arrowsmith 等，2009；Zielke 等，2012），获取这些定量参数的传统测量方法如皮尺测量、全站仪测量、实时差分（RTK）-GPS 测量等，不仅受野外自然条件限制，且受人工操作影响，会导致测量效率低、危险系数增高等问题，并使测量范围局限在较小的区域内（刘静等，2013；王朋涛等，2016；Bi 等，2017）。

20 世纪末发展起来的激光雷达扫描技术LiDAR 使快速获取高精度地形数据成为可能（Hudnut 等，2002；刘静等，2013；陈涛等，2014）。LiDAR 的优势不仅在于精度高、扫描速度快，且可利用多重回波技术进行地面点和非地面点的区分，以此排除植被对测量精度的影响，更适用于植被发育较好的地区。然而LiDAR 也有其局限性，由于LiDAR 整合了激光扫描仪、高精度惯导系统（IMU）、GPS、成像装置等设备，通过高空机载或无人机载LiDAR 设备均会导致造价较高；另外，LiDAR 虽能在弱光下进行数据采集，但如果空气中浮尘等颗粒物较多，会对激光光束产生影响，同时由于激光波束较窄，难以用于搜索目标测量，使LiDAR 难以推广使用（Johnson 等，2014；赖旭东等，2017；佘金星等，2018；罗达等，2019；Okyay 等，2019）。

近年来，移动摄影测量技术SfM 的发展极大地提高了野外中小区域测量工作效率。该技术拥有大多数LiDAR 技术的优势，包括可绝对定位、重复多次测量及获取高分辨率地形数据等，且SfM 技术更简单方便，成本较低（Westoby 等，2012；Wei 等，2013；刘静等，2013；Johnson 等，2014；王朋涛等，2016；Bi 等，2017；张志文等，2021）。但利用无人机搭载相机进行摄影时，需在地面设置控制点，对测量结果进行校正，会降低测量效率，增加工作量。Harwin 等（2012）研究了添加控制点的必要性，但研究前提是利用摄影测量的飞行器均未搭载任何RTK 设备。针对该问题，使用搭载有RTK 模块的无人机在野外分别采用RTK 和非RTK 两种模式进行摄影测量。非RTK 模式下在测量区域使用Trimble R10 差分GNSS 均匀采集了地面控制点，并采集了多条地形剖面线。在室内分别将RTK 模式下生成的数字高程模型（DEM）与非RTK 模式并结合地面控制点生成的DEM，以及Trimble R10 差分GNSS 采集的地形剖面线进行对比，以此讨论确定搭载网络/基站RTK 模块的无人机在移动摄影测量中发挥的作用。

1 SfM 移动摄影测量基本原理与数据处理流程

SfM 移动摄影测量是使用运动着的相机从多个视角获取所拍摄物体的多视角图像集，由此推算出相机位置和姿态，从而重建三维数字表面结构的技术方法（Ullman，1979；Westoby 等，2012；李美燕，2014；杨海波等，2016；艾明等，2018）。基于SfM 重建DEM 是传统摄影测量的逆过程，在该过程中，二维图片内的点利用一定算法转换为三维坐标内的点，通过不同位姿相机拍摄的图片中大量重复的同名点实现（Tomasi 等，1992；Wei 等，2013；李美燕，2014）。

一般SfM 重建地形工作的过程包括影像特征检测、同名点立体匹配、相机位姿标定、三维重建等。其中影像特征检测、同名点立体匹配一般利用Lowe（2004）提出的SIFT（Scale Invariant Feature Transform）同名特征点匹配算法，用于进行检测、匹配，经检验，已有研究认为该算法较好地解决了拍摄过程中由于相机运动产生的图形变形问题（陈志雄，2008；杨艳伟，2009；郑辉，2010）。基于匹配完成的特征，进行相机位姿标定工作，利用迭代光束平差方法可精确求得相机的位姿，并初步获得由一系列同名点构建的较稀疏的点云框架（Harwin 等，2012；Mancini 等，2013；Lucieer 等，2014；Bemis 等，2014；Javernick 等，2014）。获得稀疏的点云框架后，可进一步进行高精度处理，主要基于多视角立体测量原理逐像素在影像间搜索匹配生成大量的匹配点，得到更密集的点云数据（Johnson 等，2014）。对密集点云数据进行绝对坐标校正和空间插值。最终得到具有真实空间地理坐标的点云和DEM 等地形数据。

网络RTK 移动摄影测量与传统移动摄影测量的区别主要在于通过在无人机上搭载RTK 模块，利用网络RTK 进行实时差分，并将坐标信息记录在照片的中心点，每张照片可利用SIFT 算法进行同名点匹配校准，也可通过自身携带的坐标信息进行自校准，从而提高测量精度（图1）。

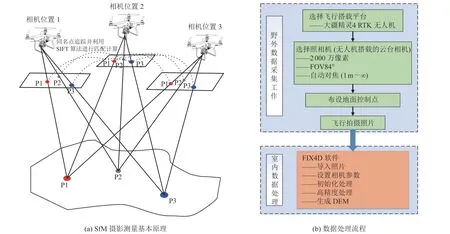
图1 SfM 摄影测量原理与数据处理流程Fig. 1 SfM principle and data processing flow chart

2 测量区域及数据采集与处理

本次测量区域选为祁连山北缘白杨河一带（图2），跨越白南断裂与白杨河背斜（闵伟等，2002），地形起伏较大，测量区域内发育因白杨河背斜形成的5 级河流阶地（刘睿等，2017），阶地面上多为砂砾石，植被稀疏，适合开展SfM 摄影测量工作（James 等，2012；Fonstad 等，2013）。

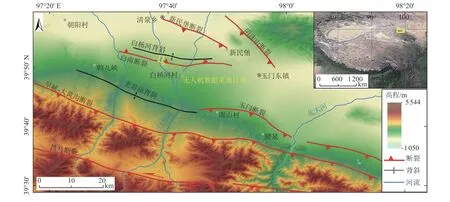
图2 测量区域及其周围构造Fig. 2 Schematic diagram of the survey area and its surrounding tectonics

采用大疆精灵4 RTK 型四旋翼无人机（图3（a））对选定的测量区域进行影像数据采集。无人机搭载的云台相机有效像素为2 000 万，相机广角为84°，自动对焦距离为1 m～∞，上述参数可保证照片清晰度，便于后续处理过程中同名点的特征提取与匹配。

为更直接地进行数据对比，在相同测量区域、飞行高度及重叠率的条件下，分别采用RTK 模式和非RTK 模式获取数据，并在测量区域内均匀地布设14 个地面控制点，地面控制点为边长47 cm 的红/黄色海绵纸（图3（b）、（c））相间排列，其表面较粗糙，对阳光的反射方式为漫反射，有利于相机在多个角度进行拍摄，且进行相控点刺点时更方便。地面控制点坐标采用Trimble R10 实时差分GNSS 接收系统（实时动态测量水平精度10 mm±1 ppm RMS，垂直精度20 mm±1 ppm RMS）在海绵纸中心进行采集，保证了校正数据的精确性（图3（d）、（e））。

图3 测量用无人机及地面控制点采集系统Fig. 3 UAV for surveying and ground control point acquisition system

2 次摄影测量过程均采用割草机式飞行路线，设置的飞行高度均为100 m，照片航向重叠率均为80%，旁向重叠率均为70%。采集每套数据时需3 个架次，拍摄过程历时约75 min，拍摄有效照片917 张。采用集成SfM 算法的Pix4D 软件进行数据处理，处理设备采用英特尔至强八核处理器的图形工作站，内存为128 G。

首先，将拍摄的照片导入Pix4D 软件，导入前剔除质量较差、成像模糊的照片。然后，设置相机参数，无人机定位和相机参数信息均直接记录在照片里，利用记事本打开所拍摄的任一照片，找到记录相机焦距fx、fy，像主点坐标Cx、Cy，径向畸变校正参数k1、k2、k3，切向畸变校正参数p1、p2，并设置相机参数，用于对SfM 处理数据结果进行校正。需说明的是，Pix4D 软件的坐标系统与照片存储位置信息存在差异，这是因为Pix4D 坐标系统是以照片左上角作为x、y轴初始原点，而照片坐标原点为照片中心。因此，处理时需用Cx、Cy加上照片文本信息中记录的相机标定的光学中心坐标，形成导入Pix4D 中照片的像中心点（图4（a）、（b））。其次，对所采集的数据进行影像特征检测，利用SIFT 算法进行同名点检测，立体匹配，恢复影像对之间的相对位置关系，获得稀疏的点云框架，并基于多视角立体测量原理（MVS）对点云进行逐像素的搜索加密，随后导入地面控制点，对生成的加密点云进行绝对坐标校正（进行RTK 模式获取的数据处理时无须添加地面控制点）；最后，生成三角网格，生成校正后带有地理空间坐标的密集点云、数字高程模型和正射影像图（Johnson 等，2014；Bemis 等，2014；魏占玉等，2015；Bi 等，2017；高帅坡等，2017）。

图4 摄影测量数据处理及成果图Fig. 4 SfM data processing and results

将基于RTK 模式获取的数字高程模型称为RTK-SfM DEM，将非RTK 模式无人机摄影测量并结合地面控制点（GCPs）生成的数字高程模型称为SfM DEM。

3 SfM 数据质量及对比分析

3.1 SfM 数据质量

采用RTK 模式进行数据处理时，根据Pix4D 生成的质量报告，每张照片上点云的中位数为70 728 个，最小为55 541 个，最大为83 516 个，平均每张照片上的点云为69 989 个，分辨率为3.85 cm。经三维空间匹配后，平均三维点云密度为315.14 个/m3，满足要求。

在采用非RTK 模式并添加地面控制点的情况下，根据Pix4D 生成的质量报告，每张照片上点云的中位数为71 169 个，最小为56 244 个，最大为83 516 个，平均每张照片上的点云为70 870 个，分辨率为3.96 cm。经三维空间匹配后，平均三维点云密度为262.65 个/m3，添加14 个控制点前、后的平均照片相对畸变为0.104%。

3.2 SfM 数据对比分析

对于空间位置（x，y，z）均有差异的2 组栅格数据，对z值进行对比时，一般采用的方法是首先以1 组栅格数据为基准，对另一组栅格数据的平面位置（x，y）进行人工几何校正，然后将校正后的2 组数据根据精度需要进行重采样，进行相应的计算后可得到2 组数据在z值上的差异。但该数据对比方法较繁琐，且由于涉及人工校正因素，会在一定程度上造成人为误差，不适用于精度较高的数据对比。CloudCompare 软件是专门用于点云对比的免费软件，其基本原理是计算2 个点云之间的距离，默认方式是最近邻距离，对于比较云的每个点，CloudCompare 软件搜索参考云中最近的点，并计算其（欧几里德）距离。如果参考点云密度足够大，可采用由对比云至参考云代表的下表面的近似距离。如果参考云不够密集，最近邻距离有时不够精确。因此，利用CloudCompare 软件确定参考云中最近的点时，利用最近的点和与其相邻的几个点拟合数学模型，对参考云表面进行局部建模。从比较云的每个点到参考云中最近点的距离被到数学模型的距离所代替，这在统计上更精确，对云采样的依赖更少。CloudCompare 软件采用了更精确的二次高度函数拟合曲面数学模型2CloudCompare user manual（Version 2.6.1），2015.。

本试验采用CloudCompare 软件对2 组数据进行对比，由于前期利用Pix4D 软件生成DEM 前已生成了相应的点云数据，以生成SfM-DEM 的点云为参考云，对生成RTK-SfM DEM 的点云进行对比，为尽量减少计算量，并提高对比的精确性，对生成RTK-SfM DEM 的点云进行适当抽稀。

随机抽取对比云内部分点云数据，通过Cloud-cloud distances 与参考云进行初步对比，本次初步对比选取了100 000 个点，全部覆盖了对比云的范围，初步对比结果如表1 所示，表中RMS 是对比云与参考云之间的平均误差，也是2 套数据之间产生的系统误差。

表1 初步对比点云转换矩阵数据Table 1 Preliminary comparison point cloud transformation matrix table

初步处理目的是将2 套数据通过大量的校准点进行对比，统计2 套数据之间的空间位置差异。由图4（g）、（h）可知，2 套数据的最小高程和最大高程差值为0.83～0.86 m，说明该初步处理结果可信。

初步处理后，CloudCompare 软件会根据转换矩阵数据调整对比云的空间位置，并对2 套数据进行详细对比。本文重点分析垂向z值对比结果，共包括73 056 320 个对比值，平均值为0.048 2 m，其中95%以上的对比值＜0.05 m，可知通过初步的空间位置修正后，对比云与参考云的垂向误差均＜0.05 m（图5）。

图5 SfM-DEM 与RTK-SfM DEM 点云对比统计及误差空间分布Fig. 5 Point cloud comparison statistics and error spatial distribution between SFM-DEM and RTK-SFM DEM

由图4（g）、（h）、图5（b）可知，垂向对比值误差较小的点云分布在测量区域内部，而误差较大的点云主要分布在测量区域边缘或无地面控制点、地面控制点稀疏的区域，部分点云位于地形较陡峭的阴影区。排除地形因素影响外，造成误差较大的主要原因是参考云的地面控制点稀疏或缺少地面控制点导致的局部畸变。

3.3 无人机摄影测量生成的DEM 与DGPS 数据高程对比

基于DEM 分析（坡度和坡向）结果，并结合野外地质调查结果，对测量区域内河流阶地进行系统划分。使用Trimble R10 实时差分GNSS 分别沿河道、T1 阶地、T2 阶地、T3 阶地、T4 阶地和T5 阶地共测量6 条测线，含5 077 个DGPS 坐标点。将实时差分测量的坐标点数据导入无人机测量生成的DEM 中，在测线相同位置提取点，与6 条测线高程进行对比（图6）。

进行预处理时，已输入了相机倾斜校正与垂直校正的相关参数，在Pix4D 处理过程中已进行了相关校正，因此后续处理相对简单。利用ArcGIS 中的数值提取到点功能，将DGPS 测点文件与无人机摄影测量生成的DEM 叠加，分别将2 种模式下生成的DEM 高程值提取至DGPS 文件中，并将数据导出，进行3 组高程对比。为使对比效果图更直观，仅选择阶地发育相对集中的局部段落进行对比（图6（c）中2 个黄框位置）。将DGPS 高程、带有控制点生成DEM 高程（SfM DEM）及基于RTK 模式生成DEM 高程（RTK-SfM DEM）数据生成散点折线图（图7），并对比分析各级阶地测线高程数据差值（表2）。

由图7 可知，3 种数据之间存在系统误差，且每2 种数据之间的误差基本恒定，但RTK-SfM DEM 数据对地形的刻画更细致。由表2 可知，添加地面控制点生成的SfM DEM 中各级阶地高程值与实时差分RTK测得的高程值相差0.446～0.610 m，平均值为0.540 886 618 m；基于RTK 模式生成的RTK-SfM DEM 中各级阶地高程值与实时差分RTK 测得的高程值相差1.258～1.471 m，平均值为1.363 883 05 m，差值均为不同测量系统之间存在的系统误差。

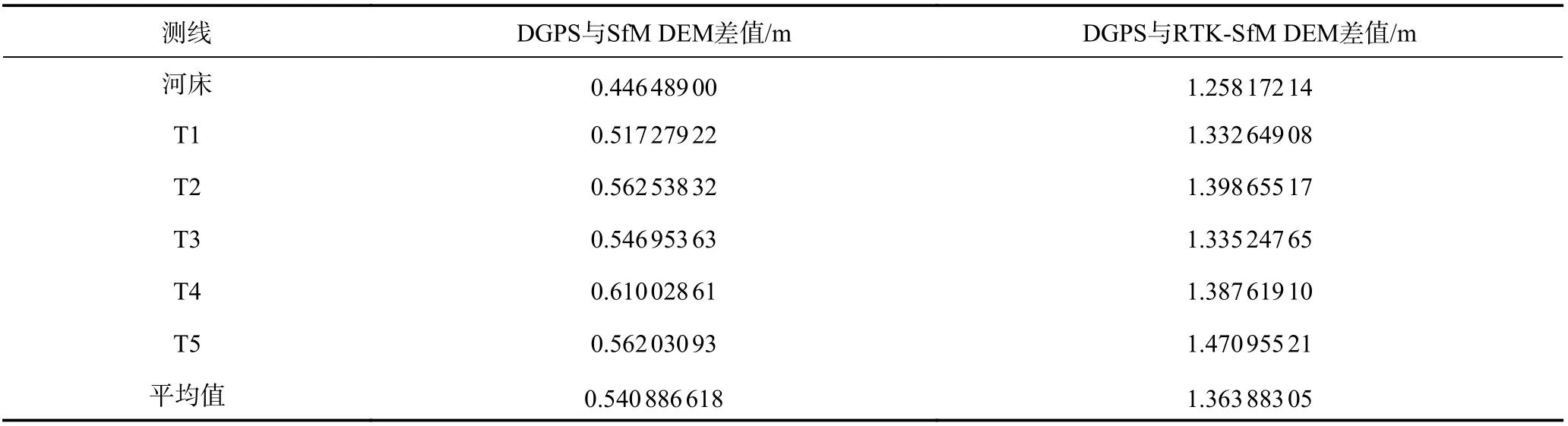
表2 3 种高程数据差值的平均值Table 2 Average value of difference of three elevation data

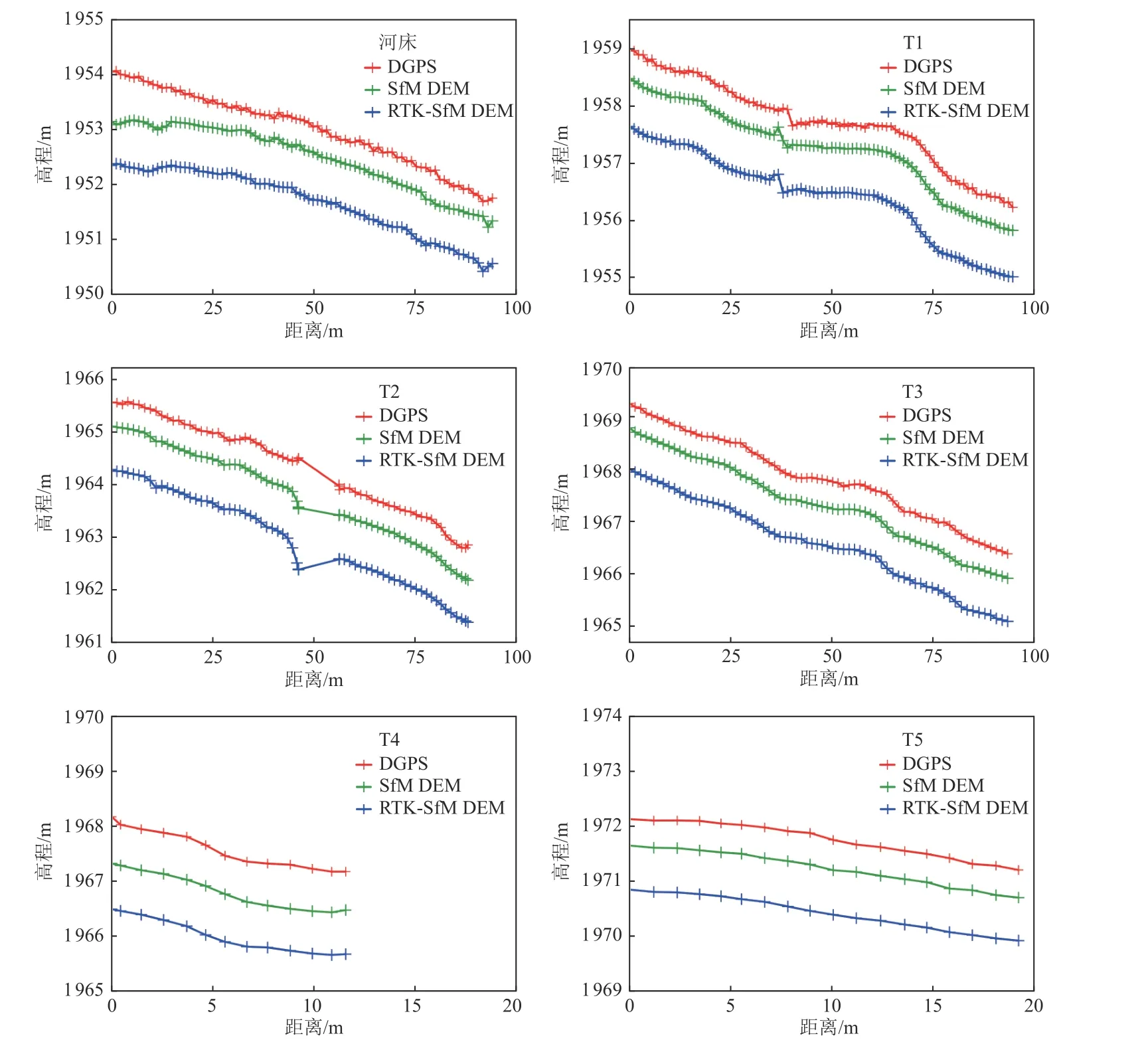
图7 DGPS、SfM DEM、RTK-SfM DEM 高程数据对比Fig. 7 Comparison of three elevation data of DGPS, SfM DEM and RTK-SFM DEM

以DGPS 数据为基准值，分别减去0.540 886 618 m 和1.363 883 05 m，以去除系统误差，然后与SfM DEM、RTK-SfM DEM 数据中提取的点高程值进行对比，得出各级阶地相对平均值与标准差（表3），以此分析2 种数据的相对稳定性。利用matlab 软件中的hisfit 绘图函数，得到利用3 种方法测得的各测线高程数据差值正态分布曲线（图8）。

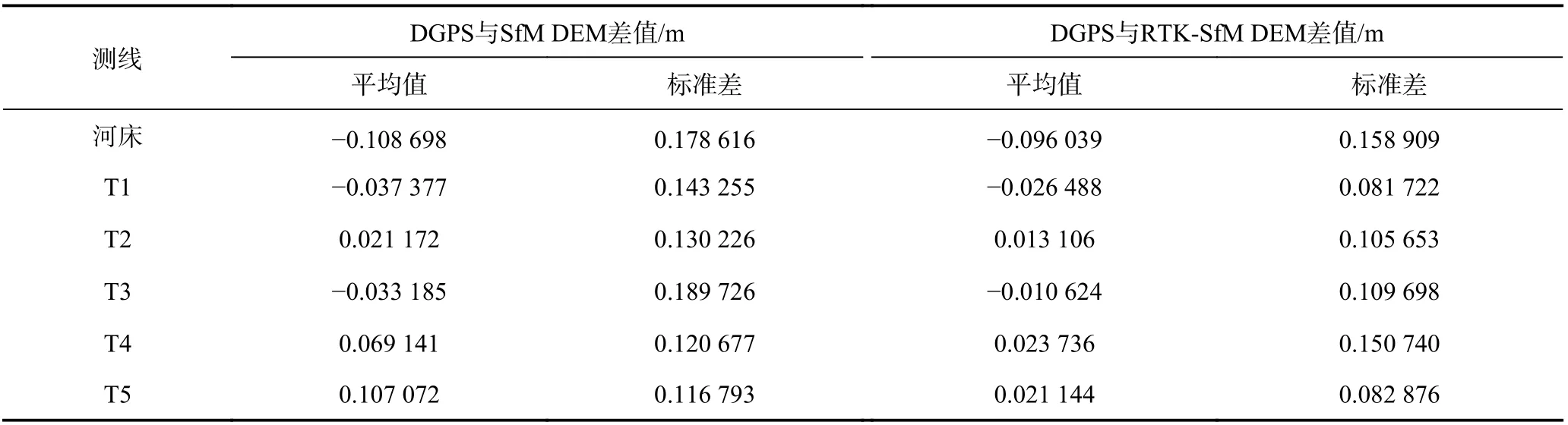
表3 去除系统误差后3 种高程数据差值平均值与标准差Table 3 Average difference and standard deviation of three elevation data after removing systematic error

由表3、图8 可知，各级阶地去除系统误差后DGPS 数据与2 种方式生成的DEM 数据之间的差值均＜0.10 m，DGPS 数据与RTK-SfM DEM 数据差值更小，大部分约为0.02 m。另外，各级阶地（除T4 阶地外）去除系统误差后DGPS 数据与RTK-SfM DEM 数据差值的标准差较小，说明如果以DGPS 数据为基准，RTK-SfM DEM 数据较SfM DEM 数据具有较好的稳定性。

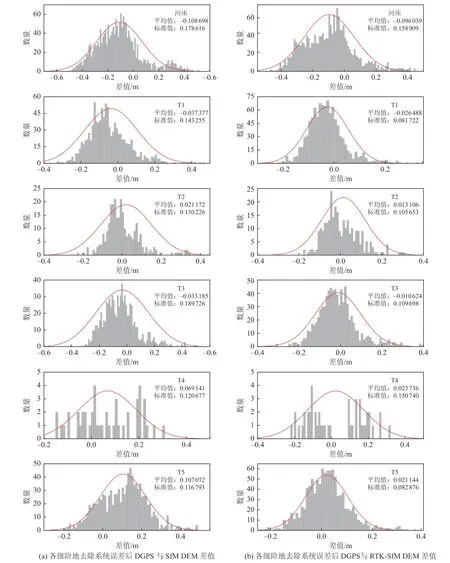
图8 去除系统误差后DGPS 数据与2 种方式生成的DEM 数据之间差值的正态分布Fig. 8 Normal distribution of the difference between DGPS data and DEM generated by the two methods after removing systematic error

4 讨论与结论

（1）对搭载RTK 模块的移动摄影测量技术获取的数据进行点云对比和与DGPS 测量数据对比，分析基于网络/基站RTK 移动摄影测量数据的垂向精度。

（2）通过对比非RTK 模式无人机摄影测量并结合地面控制点（GCPs）生成的数字高程数据SfM DEM与基于RTK 模式下获取的数字高程数据RTK-SfM DEM 点云，发现2 种数据在垂向上存在约0.85 m 的系统误差，减去该误差后，2 种数据95%以上的点云在垂向上的误差均＜0.05 m，且RTK-SfM DEM 数据畸变率更小。对比阶地面上DGPS 测量数据与以上2 种模式下获取的高程数据发现，DGPS 测量数据与SfM DEM数据存在约0.5 m 的系统误差，DGPS 测量数据与RTK-SfM DEM 数据存在约1.3 m 的系统误差，产生系统误差的原因需进一步研究。去除系统误差后，DGPS 测量数据与RTK-SfM DEM 数据差值的标准差较小，说明误差分布更集中，可知RTK-SfM DEM 数据具有更好的稳定性与更小的畸变率。

（3）笔者在山西地堑系、四川和云南地区均开展了对比工作，均存在系统误差，但该系统误差因地区不同而不同，山西地堑系约为0.7～0.8 m，四川地区约为0.5～0.6 m，云南地区约为1.1～1.2 m。笔者认为造成系统误差的原因可能为：①无人机与地面采集终端（Trimble R10 实时差分GNSS 接收系统）源椭球设置不一致；②地面采集终端的基准站开机后，静置初始化时间较短，且基准站未在已知坐标控制点上进行校正。垂向上的系统误差不会影响RTK-SfM DEM 数据的可靠性，如果数据均匀稳定且畸变率小，可满足活动构造研究对高程数据的精度要求。