基于双目内窥镜的散斑三维重建系统研究

郭俊广 谷飞飞 叶于平 宋 展,3*

1(中国科学院深圳先进技术研究院 深圳 518055)

2(中国科学院大学 北京 100039)

3(粤港澳人机智能协同系统联合实验室 深圳 518055)

1 引 言

内窥镜是一种集传统光学、人体工程学、精密器械、现代电子、数学和软件为一体的新型无损检测仪器[1]，可以扩大视距和视野，提高观察分辨率。内窥镜由于可以在受限的空间(如人体)及高温、高压、有毒有害的环境中工作，所以在医疗诊断和工业检测中成为非常重要的成像工具[2]。在工业领域，内窥镜在发动机、齿轮箱等机械不拆卸的情况下，就可以准确、清晰地检测其内部情况；在医疗领域，医生可以通过内窥镜对病人病患处进行检查，也可以将电子内窥镜作为图像采集设备来辅助微创手术。随着三维测量技术的不断发展，三维测量与三维重建在工业和医疗领域有着越来越重要的意义[3]，三维测量内窥镜成为了一个热门研究课题[4]。2006 年，Hayashibe等人研究了一种基于激光扫描三维技术的内窥镜系统[5]，实现了内窥镜的立体成像；2015 年，Yang 等人提出了一种融合三维超声波扫描技术的内窥镜手术跟踪系统[6]，将超声构造的场景几何与内窥镜视觉结合，解决了尺度模糊和特征点不足的问题；2016 年，Furukawa 等人设计了一种内置衍射光学元件(DOE)投影仪的内窥镜[7]，并提出了一种基于网格线的网格模式与间隙编码，成功地重建了人体的软组织形状；2017 年，周亭亭提出了基于散斑结构光的双目电子内窥镜技术[8]，针对腹腔弱纹理真实场景，解决了被测物体表面弱纹理导致误匹配问题，并实现了较高分辨率的测量精度。

目前，美国和日本对内窥镜的研究在全球处于领先地位，美国韦林公司的 Mentor Visual iQTM系列[9]内窥镜产品和日本奥林巴斯公司的 EVIS LUCERA ELITE 电子内窥镜系统[10]，基本垄断了国内外电子内窥镜的高端市场。这些产品都具有测量长度、深度、周长和面积的功能，但不具备稠密重建的能力，且产品价格不菲，售后服务费用高昂。以上海澳华内镜股份有限公司和北京爱迪泰克科技有限公司等为代表的国内企业，其内窥镜直径可以做到 1～10 mm，但不具备立体重建测量功能。2019 年，沈阳沈大内窥镜有限公司和北京德朗检视科技有限公司分别推出了一款具有三维测量功能的内窥镜产品，其探头外径分别为 6 mm 和 8 mm，与国际高端三维内窥镜相比，探头尺寸偏大，一定程度上限制了应用场景。因此，研发一款小尺寸且具备三维重建功能的电子内窥镜具有重要意义。

本文提出一种小尺寸探头(探头直径为3.9 mm)，其包含两个分辨率为 640×360(23 万)像素的 CMOS 摄像机，基于散斑结构光的高精度 3D 内窥镜系统。该内窥镜探头可以进入狭小空间观测目标物体，满足大部分应用场景。由于双目内窥镜的基线较窄(基线为 3.5 mm)，使用光学微型孔径镜头会使拍摄出来的图片存在大畸变、清晰度不足等不利情况。为此，本文提出一种双目标定参数优化方法，来降低图片畸变的影响，提高了双目内窥镜的标定精度；针对左右像素的匹配精度直接影响内窥镜测量精度的问题，本文提出一种沿着左右相机坐标轴分别旋转两次的极线校正算法，可以实现左右图像共面行对准，进而达到像素的精确匹配；针对实际场景中的弱纹理或无纹理区域，本文提出了基于散斑结构光的半全局立体匹配方法，即将散斑图案投射到目标物体表面来增加特征信息后，利用半全局立体匹配算法获取所拍摄图像的视差图，并通过三角测量原理获取三维点云数据，实现三维重建。

2 系统工作原理

本文采用基于散斑结构光的双目内窥镜系统，其硬件主要包括散斑照明系统和双目内窥镜系统。其中，散斑照明系统采用的投影仪是安华公司生产的 M8M-NIR 投射模组，显示芯片为DLP4500NIR，物理分辨率为 912×1 140，最大投射频率为 4 225 fps；双目摄像头所使用的图像传感器为 OmniVision 公司的 OVM9724 图像传感器，有 GND、VDD、P－(负极信号线)、D＋(正极信号线)4 个引脚，光学尺寸为 1/9 in，分辨率为 640×360，帧率最高为 30 fps，内窥镜探头直径为 3.9 mm，相应基线为 3.5 mm，探头的两个摄像头旁各有一个发光二极管作为冷光源进行照明。使用过程中，散斑照明系统首先将散斑图案投射到待测目标物体表面，然后对双目内窥镜拍摄带有散斑图案的图片进行处理。

采用散斑结构光技术进行双目三维重建的步骤包括：双目相机标定、极线校正、立体匹配和三维重建。其中，立体标定、极线校正和立体匹配准确性会影响三维重建精度，且高精度的立体标定和极线校正是实现双目左右图像特征匹配的前提。因此，本文着重研究高精度的双目标定算法和极线校正算法。双目内窥镜系统示意图如图 1所示。系统算法流程主要分为以下 4 个步骤：

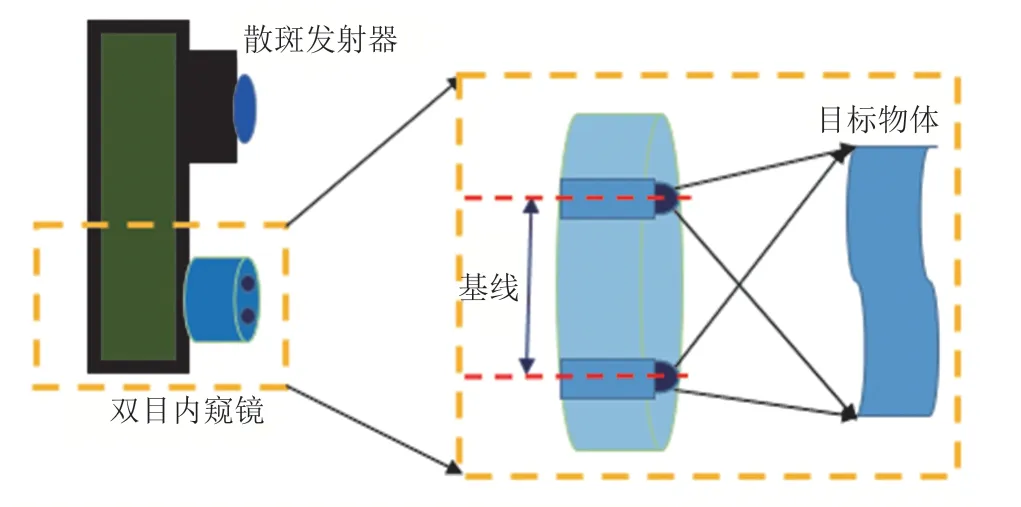
图1 系统示意图Fig. 1 System diagram

(1)系统标定，通过对双目内窥镜系统进行立体标定，得到左右摄像头各自的内参数和两者之间的外参数；

(2)非线性标定优化，将(1)中得到的立体标定参数作为初始值，在传统方法所定义的重投影误差目标函数基础上，增加定义平面度、距离、角度 3 个度量误差函数，通过构建多目标非线性优化函数，求解双目系统的最优标定参数；

(3)极线校正，为了提升立体匹配的速度和准确率，提出一种沿着左右相机坐标轴分别旋转两次的极线校正方法；

(4)立体匹配和三维重建，根据(1)～(3)得到最优的双目内窥镜内部和外部参数，沿着校正后的极线进行特征匹配，利用三角测量原理重建目标物体的三维信息。

2.1 系统标定

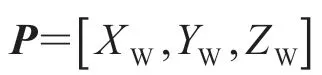
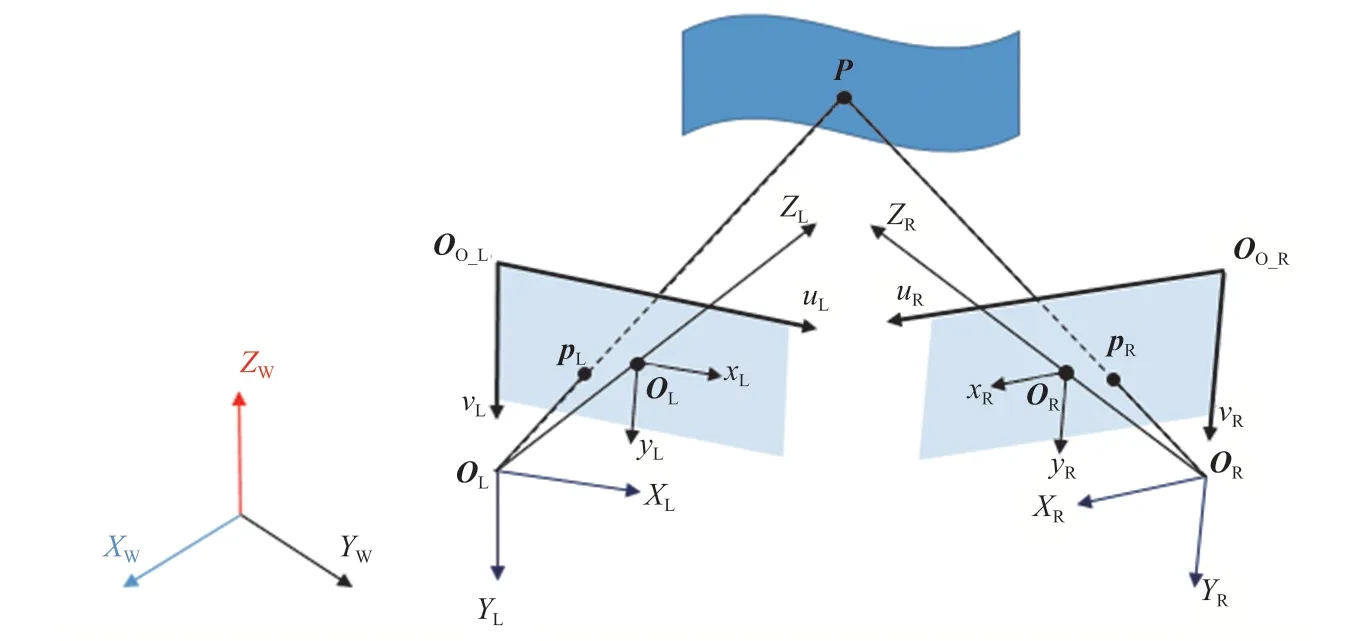
图2 双目成像几何模型Fig. 2 Geomagic model of binocular imaging

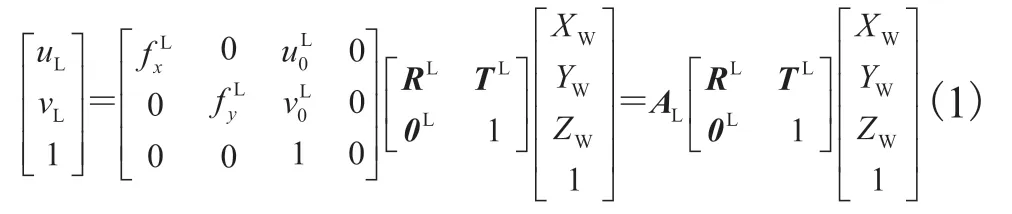
由于相机镜头的制作、安装等工艺问题会导致图像发生畸变，所以需在双目成像几何模型中加入非线性畸变校正项，镜头畸变校正公式如公式(2)所示：

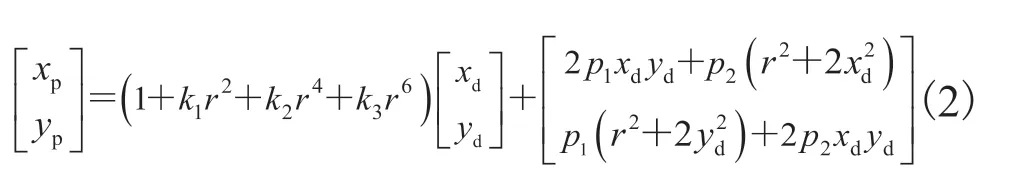
其中，xd,yd为畸变的位置；r2为畸变位置到畸变中心径向距离的平方；k1,k2,k3为径向畸变系数；p1,p2为切向畸变系数；xp,xp为畸变校正后的新位置。如果有n幅标定图像，每幅标定图像上可以提取m个特征点，那么加入畸变系数后，使用 LM(Levenberg-Maquardt)优化算法[14]对包含所有参数的目标函数进行优化求解，最终得到优化的相机参数。以左相机为例，构造的非线性目标函数如公式(3)所示：

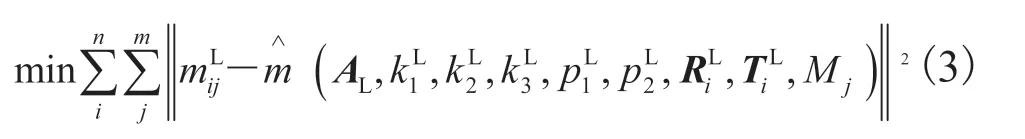
其中， 为左相机拍摄第i幅图像中的第j个特征角点的像素坐标； 为左相机的镜头畸变系数， , 为左相机所拍摄的第i幅图像的相机坐标系对应于世界坐标系之间的旋转矩阵和平移向量；为第i幅图像中空间坐标点Mj在图像上的重投影。右相机的标定方法与之相同，标定后可以分别得到内部参数AR和外部参数RR,TR。

联立左右相机标定后的内部参数及相对于世界坐标系的外部参数，求得左右相机之间的旋转平移关系，以左相机坐标系为参考坐标系，双目系统的旋转矩阵R和平移向量T表述如下：

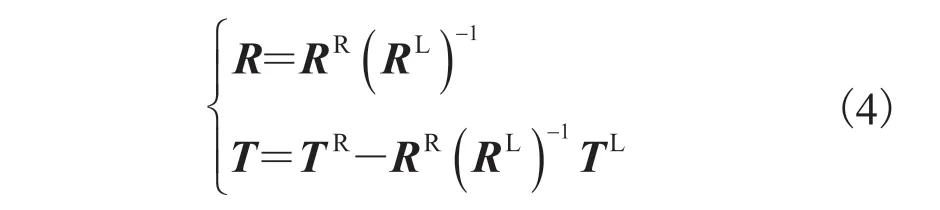
该标定方法通过最小化参考点的二维重投影误差来优化标定结果，但最小重投影误差并不等于最小重建误差[15]，因为双目内窥镜的基线窄，立体像对视差小[16]，标定的微小误差就会引起很大的重建误差。为了提高三维重建精度，在 Nie 等人提出的针对单目结构光系统的标定优化算法[17]的基础上，本文研究了一种基于三维的标定优化方法。该方法将基于双目内窥镜系统的所有标定参数作为全局优化问题来处理：将初始标定的结果作为初值，通过构造一些目标函数，达到最小化三维测量误差、实现最优标定结果的目的。

2.2 标定优化

为了保证物体的平整度，采用一种反射率均匀的平面棋盘格玻璃板进行优化，如图 3 所示。平面棋盘格玻璃板上标记点之间的距离L非常精确，其以基准面为基础，定义了平面度误差、距离误差和角度误差 3 种三维测量误差准则。将双目内窥镜系统通过第 2.1 节得到的所有标定参数作为变量，可以建立一个多目标非线性优化问题，以初始标定结果作为初始值，求解出三维测量误差最小的最佳标定参数，标定优化工作流程图如图 4 所示。

系统根据棋盘格亚像素角点检测算法[18]，首先提取棋盘格玻璃板上的亚像素角点坐标，获得一组图像点(cp)，同理，根据亚像素精度检测算法得到图 3 上所标注的标记点cm；然后根据初始标定参数和双目三维重建算法[19]，cp和cm的三维坐标可以表示为Cp和Cm；最后在三维重建点Cp和Cm的基础上，通过构造 3 个度量误差目标函数，构造出多目标优化问题，用于精确地估计系统标定参数。3 个目标函数定义如下：

图3 用于系统参数优化的棋盘格玻璃板Fig. 3 Illustration of checkboard glass plate used for system parameters optimization

(1)平面度误差：将用于重建的参考平面看作是一个完美的平面，即在不考虑标定误差和重建误差的情况下，Cp的平面度误差为 0。在此基础上，提出了最小二乘拟合法[20]，假设参考平面提取角点的数目为N，第i个点到拟合平面的距离为gi，则平面度误差Dp可以表示为：

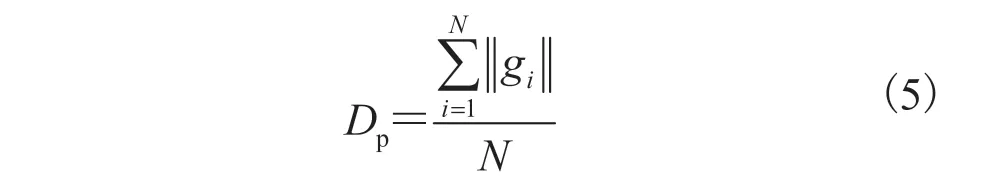
(2)距离误差：对于每个标记点 ，它与所有相邻标记点在水平和垂直方向上的平面距离表示为lj，参考平面有 4 个角，那么，距离误差函数Dd可以表示为：

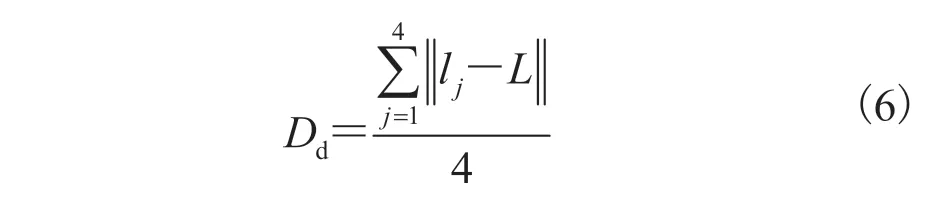
其中，L为参考平面相邻两个标记点之间的长度。

(3)角度误差：平面度误差和距离误差仍然不足以保证很好的重构参考面，考虑到仿射变换可能是由于初始标定参数不准确引起的，因此，构造一个目标误差函数来评价标记点(图 4 已标出)之间的角度。对于每个标记点 ，通过相邻的标记点连接起来，可以计算角度θj。θ的理论参考值为 90°，那么，角度误差函数Dθ可以表示为：

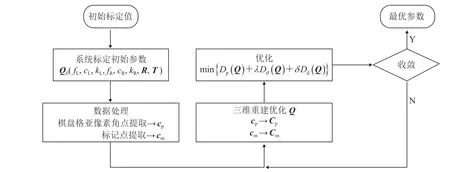
图4 标定参数优化流程图Fig. 4 Flow chart of the calibration parameters optimization

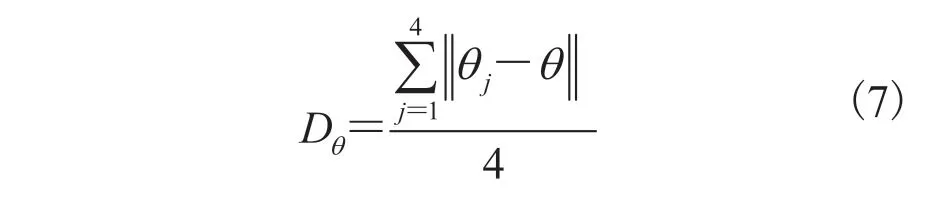
综上所述，共需优化 30 个参数，包含 8 个内参数(左右相机各 4 个)，12 个外参数(左右相机之间旋转矩阵R中有 9 个，平移向量T中有 3 个)和 10 个镜头畸变参数(左右相机各有 5个)。若在优化过程中不考虑相机传感器的倾斜因子 ，那么所有需要优化的参数用向量Q表示为：

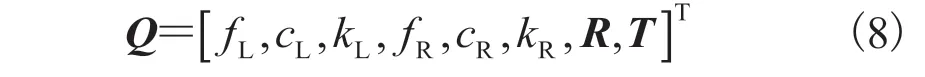
通过常规的标定程序[21-23]得到的初始值Q0，可建立一个多目标优化问题，如公式(9)所示：

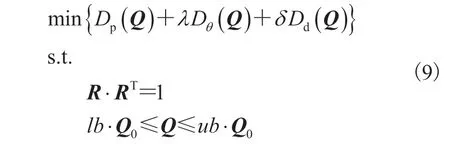
其中，第一约束 用来确保旋转矩阵R的正交性，第二约束用来设置参数的取值范围。下边界系数lb和上边界系数ub按照经验值设置为 [0.9,1.1]，使用权重因子 和 来平衡 3 个误差函数的影响，这 3 个误差函数可以通过经验来实际调整权重因子的大小，使其满足。在实际实验中， 通常设置为 1， 设置为 1.44[17]。

本研究中使用 MATLAB 优化工具箱中提供的优化函数“fmincon”，用以求解多目标优化问题，该函数基于序列二次规划方法[24]求解。本实验用三维度量代替了二维重投影，实验结果表明，前者测量结果准确性更高。

2.3 极线校正

双目摄像机系统的立体匹配是在左右相机严格对齐的理想情况下进行的，因此需在立体匹配前进行极线校正，即将左右相机成像平面校正成共面行对准。立体图像极线校正示意图如图 5 所示。

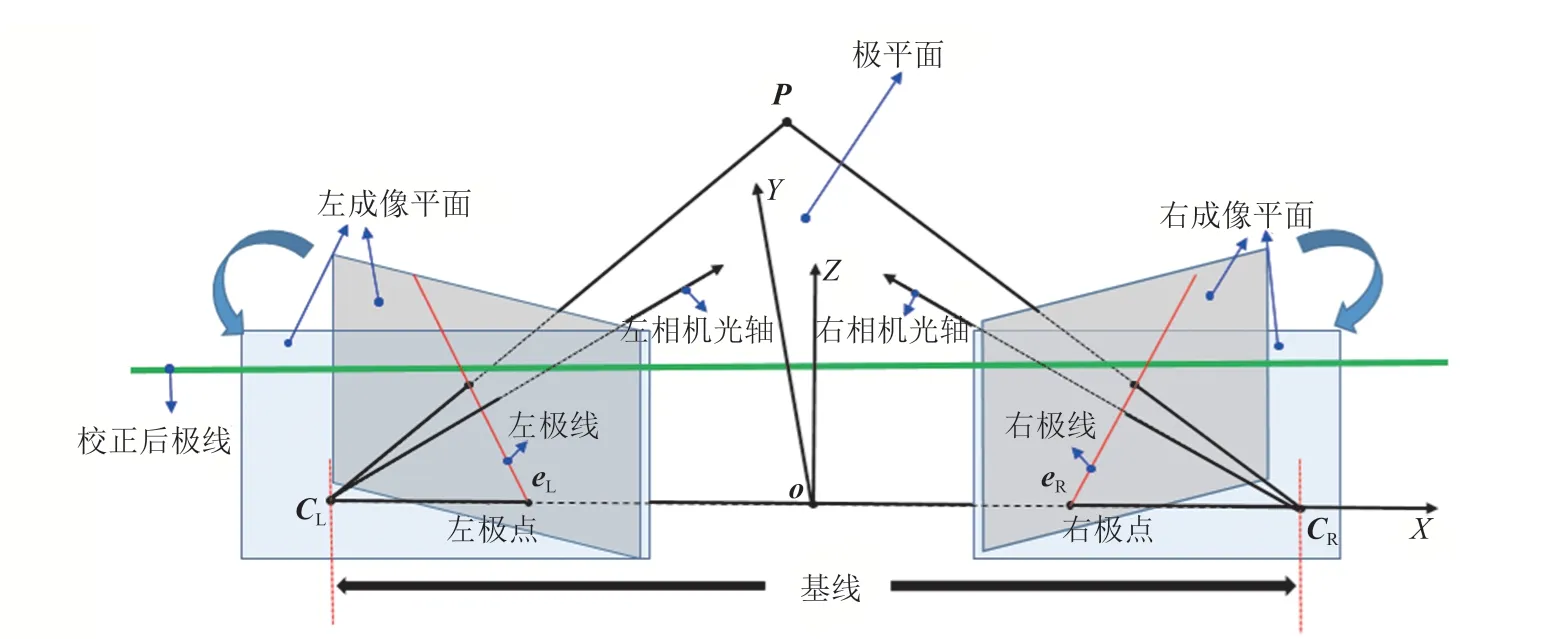
图5 立体图像极线校正Fig. 5 Epipolar rectification of stereoimages

以左相机坐标系为参考坐标系，在进行极线校正前，右相机坐标系对左相机坐标系的相对变换为。为了使所有的极线平行以辅助立体匹配，校正后的左右相机坐标系应水平对齐，即它们之间只有平移关系[25]。

本文提出一种左右相机坐标轴双次旋转的极线校正方法，具体过程如图 6 所示。假设左右相机光轴之间形成的角度为 ，为了最小限度地旋转左右相机并使其坐标系具有相同的方向，那么把左右相机沿相反方向都旋转 ，这正好是左右相机之间旋转关系R的一半。引入旋转向量om，把R和 联系起来，其中，om是一个3×1 的向量，可以将 3×3 的矩阵R描述得更加紧凑些。向量om的方向为旋转轴，om的模为绕旋转轴旋转的角度。因此，向量om与旋转角度 的关系为，根据罗德里格斯(Rodrigues)变换公式得到左相机的旋转矩阵，如公式 10 所示：

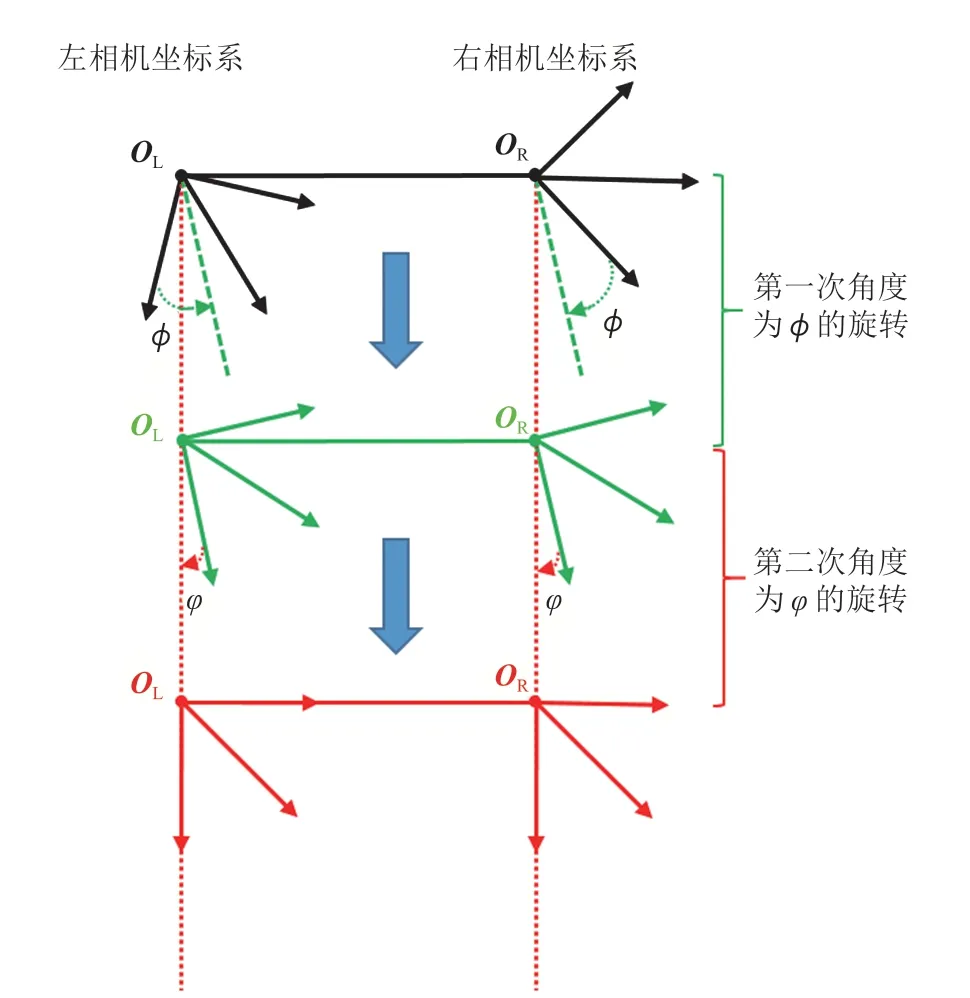
图6 极线校正的两次旋转Fig. 6 Epipolar rectification by two rotations

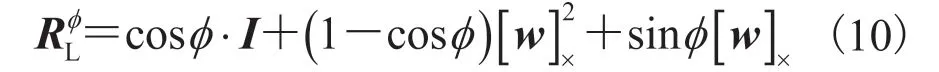
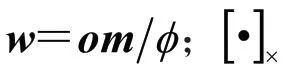
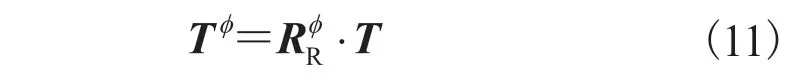
经第一次旋转后，虽然左右相机的新光轴是平行的，但是它们与OL和OR连线所构成的轴不垂直(图6)。因此，需要对左右相机坐标轴再进行一次角度为 的旋转，令，使轴和平移向量对齐。新旋转轴的方向可以用和计算得到：

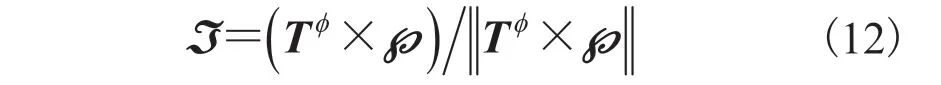
第二次旋转的角度 可以通过下式得到：

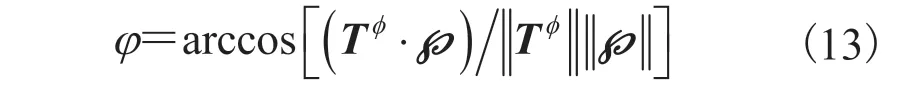
通过上述两次旋转，可以得到极线校正后左右相机的旋转和平移关系：

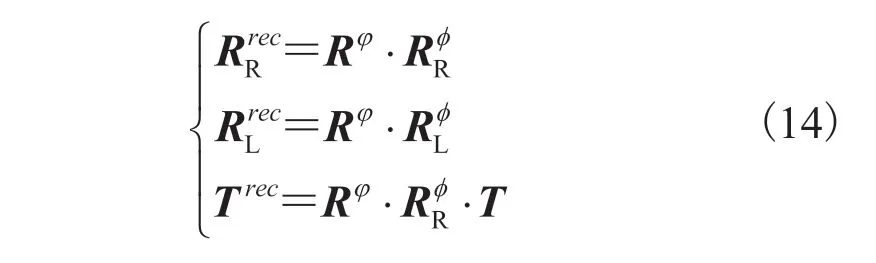
其中，rec表示经过极线校正后的参数。

对于双目相机的成像中心，通常选取左右相机的成像中心的平均值作为校正后的双目相机中心位置，但是这在实际中并不准确[26]。这是因为校正后的图像或多或少受到旋转和扭曲的影响，成像中心的位置也可能随之受到影响。所以，在确定了其他内、外参数后，可以根据已知参数求解矫正后的图像中心位置。首先，假设校正后的成像中位在[0,0]T处，如图 7 所示，将原始图像的 4 个顶点{v1,v2,v3,v4}投影到极线校正后的坐标系中，得到校正后的图像中心k0：

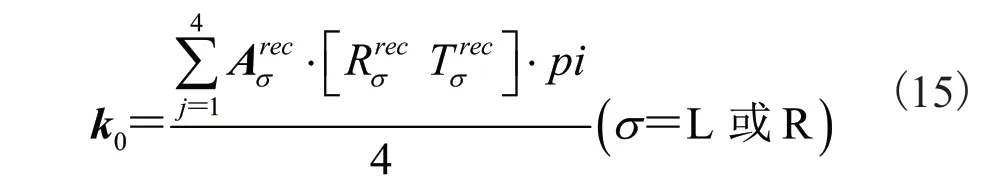
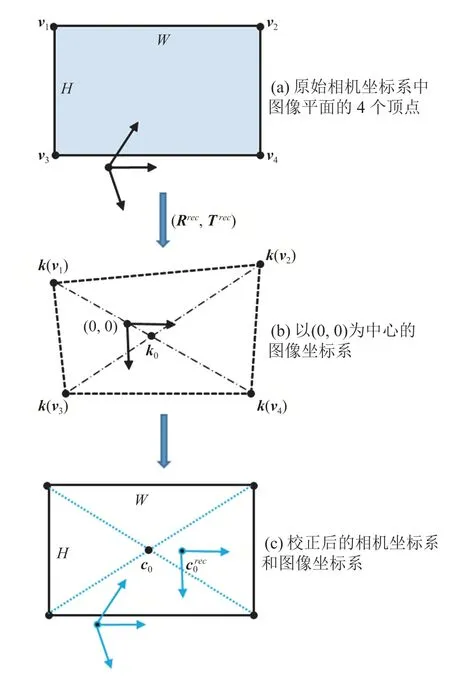
图7 极线校正后图像中心的确定Fig. 7 Determination in imaging center after epipolar rectification

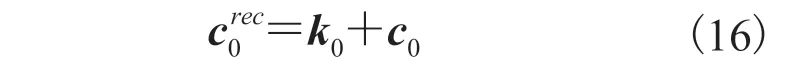
2.4 立体匹配和 3D 重建

精确的特征匹配在三维重建中起到至关重要的作用。根据第 2.1～2.3 节，首先得到优化的左右像机的内外参数，其次沿着校正后的极线进行特征匹配，再次基于三角测量原理计算场景的视差信息，最后经过三角重建即可进行三维场景的测量。与局部匹配算法和全局匹配算法相比，半全局立体匹配算法可以实现获得高质量深度图和运行效率之间的平衡[27]，但针对纹理稀疏或无纹理区域容易出现错误匹配，本文利用散斑结构光的特征信息，通过将散斑投射到缺乏纹理特征信息的目标物体表面，基于半全局立体匹配算法完成对缺乏纹理特征表面的三维重建目标。本文采用相同的重建方法分别对无散斑投射和有散斑投射的棋子进行三维重建，实验结果如图 8 所示。通过对图 8 分析可得，经散斑投射的棋子重建出的点云更加稠密，具有更好的重建效果。

图8 有无散斑条件下的重建点云结果Fig. 8 Point cloud reconstruction results of with or without speckles

左右双目相机都可看作是水平放置的针孔相机，其光圈中心都位于x轴上，两中心之间的距离称为双目相机的基线。三角测量原理的几何模型如图 9 所示，OL和OR分别为左右相机的光圈中心，f为焦距，uL和uR为成像平面的坐标，按照坐标系方向，图中标出的距离为－uR。将左相机坐标系与世界坐标系重合，假设空间有一点，在左相机和右相机上的投影点分别为和，根据透视投影变换和图 9 中与的相似关系，有：

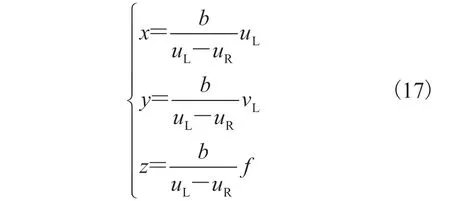
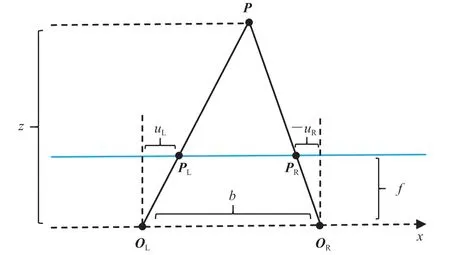
图9 三角测量几何模型Fig. 9 Geometric model of triangulation

3 实验结果

3.1 实验设备

本实验装置由双目模块和散斑光源组成。其中，双目模块由两个定焦 RGB 相机(分辨率640×360，USB2.0 接口，帧率 30 fps，焦距 5 cm)和一台 DLP4500 光机(分辨率 912×1 140，投射比 1:1.2)组成，实验平台放置方式如图 10 所示。

图10 实验平台搭建Fig. 10 The experimental setup

3.2 双目内窥镜系统标定结果与分析

双目内窥镜系统利用张氏标定法[12]标定初始参数，通过改变棋盘格(角点 7×7，每个方格大小 3 mm×3 mm)的摆放姿态获得 23 组不同的视图，如图 11 所示。

图11 左右相机获得不同位姿标定图像Fig. 11 Calibration images with diあerent orientation captured by left and right camera

双目内窥镜系统初始标定参数如表 1 所示。初始标定之后，根据第 2.2 节提出的首先利用基于三维的标定优化算法对初始标定后的参数进行非线性优化，通过对比标定优化前后的两组参数计算出该节所述的 3 个度量误差函数，如表 2 所示。然后将双目内窥镜系统进行沿左右相机坐标轴旋转两次的极线校正操作，其极线校正后的标定参数如表 3 所示。

表1 系统初始标定参数Table 1 Initial calibration parameters of the system

表3 系统优化后的标定参数Table 3 Calibration parameters after system optimization

用于标定优化的平面棋盘格玻璃板(图 3)还可用于评估标定参数的精度，即通过优化前后的标定参数提取平面棋盘格的角点，提取角点拟合平面误差如图 12 所示。由图 12(a)和图 12(b)可知(R-square 的范围为[0,1]，值越接近 1，表示平面拟合程度越好)，优化前后的平面度误差分别为 0.845 3 mm 和 0.999 2 mm，优化后的标定参数使角点平面拟合度精度提高近 18.21%。其中，对第 2.2 节所建立的 3 个度量误差函数的优化结果对比见表 2。

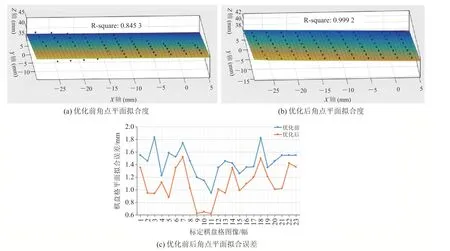
图12 棋盘格角点拟合平面误差Fig. 12 Chessboard cornor fitting plane error

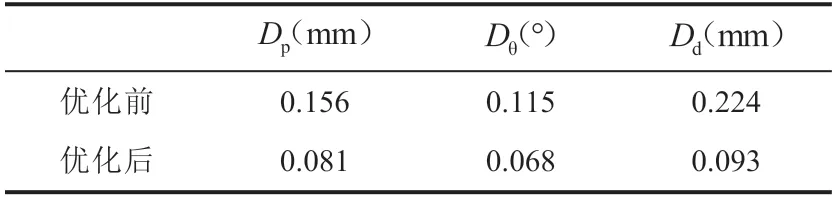
表2 系统优化前后的度量误差Table 2 Metric errors with and without system optimization

标定优化是在离线情况下进行的，从输入初始标定参数作为初始值开始，到迭代次数大于最大迭代次数停止，求解最优标定参数的整个过程耗时 55 s，因为目标优化函数公式(9)中所含的3 个误差函数在参考平面(图 3)中提取的点的数量较少，计算过程中计算量较小，因此整个标定优化时间也较短；三维重建是在线进行的，在对图 8 中的棋子进行三维重建时，系统首先读取双目内窥镜拍摄带散斑图案的二维图片，然后利用最优标定参数进行图像极线校正、半全局立体匹配，最后进行三维重建，图 8 中棋子的三维重建过程运行时间约为 1.042 s，而在实际中，三维重建的时间与待重建场景的纹理丰富度、立体匹配算法选择的关系很大。

3.3 对比实验

为了测试本文双目内窥镜系统的重建精度，将基于三维的标定优化方法和沿坐标轴旋转两次的极线校正算法得到的标定优化参数，与传统标定方法[12]得到的标定优化参数分别进行三维重建并作对比。本文采用球体、圆锥体和标准平面作为重建对象，其中，球体直径为 20 mm，加工精度 ±20 μm；圆锥体直径为 20 mm，加工精度 ±10 μm；标准平面 25 mm×35 mm，加工精度 ±10 μm。重建结果如图 13 所示，图中从上到下分别对应圆锥体、球体和标准平面重建的结果。精度对比如表 4 所示，由表 4 可知，本文系统对圆锥体的三维测量误差为 0.098 mm，而传统方法重建的误差为 0.145 mm，重建误差比本文系统高出 48.0%；对于球体，本文三维测量误差为 0.112 mm，而传统方法三维测量误差为 0.124 mm，重建误差比本文系统高出 10.7%；对于标准平面，本文三维测量误差为 0.270 mm，而传统方法三维测量的误差为0.361 mm，重建误差比本文系统高出 33.7%。综上所述，双目内窥镜散斑系统有较高的三维测量精度。

图13 本文方法与传统方法三维重建精度比较Fig. 13 Comparison of 3D reconstruction by the traditional and proposed method

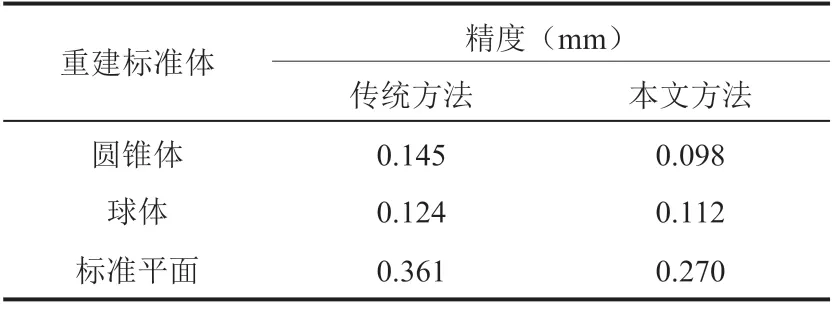
表4 三维测量精度对比Table 4 Comparison of 3D measurement accuracy

3.4 实际应用场景三维重建

为了评估本文基于双目内窥镜的散斑三维重建系统的有效性和准确性，分别对猪小肠内壁和牙齿的立体图像进行三维重建，其原始图像、散斑投射图、深度图、带纹理点云图及重建的 3D模型如图 14 所示。

由图 14 可知，图像纹理信息越丰富，其表面形状恢复的越好。重建模型图与原图相比，虽然出现残缺，但是其完成重建部分的整体形状符合人们的视觉直观感受，满足部分应用场景。如在医疗领域，通过基于双目内窥镜的散斑三维重建系统可完成体内三维场景深度图的构建，帮助医生在某些复杂病变情况下完成对病人精确诊断治疗。

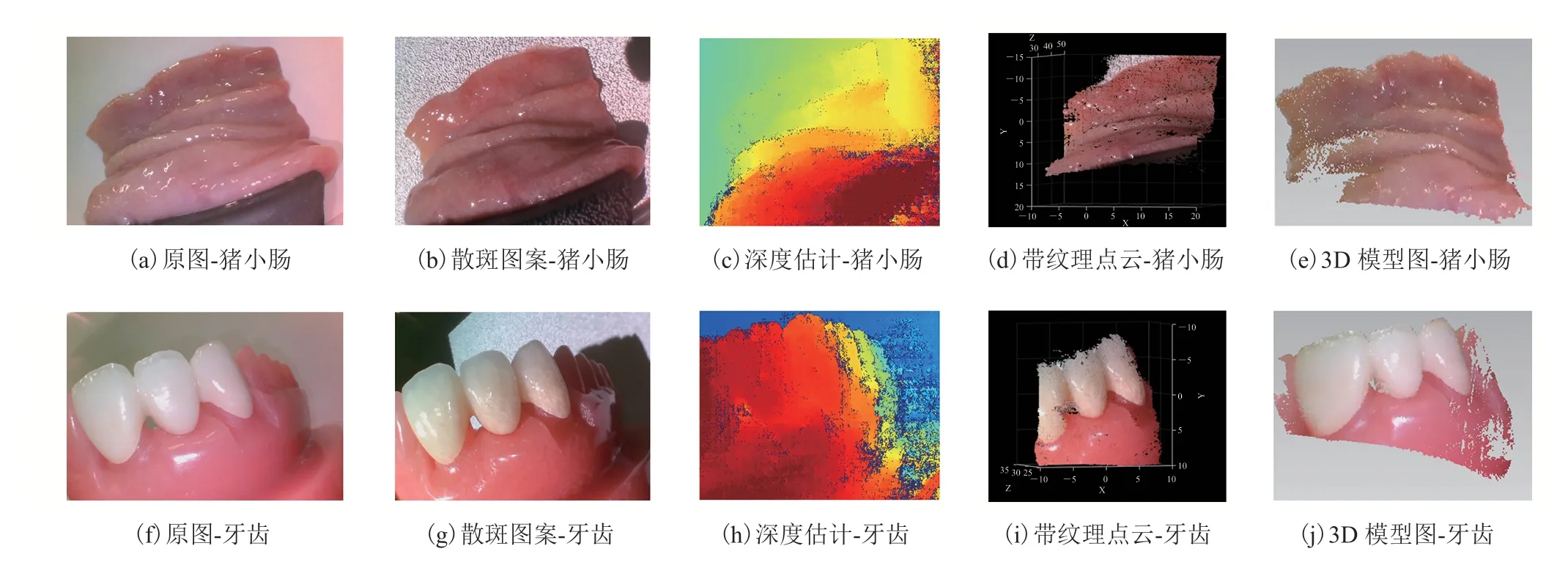
图14 本文系统对猪小肠内壁和真实牙齿的重建结果Fig. 14 Reconstruction result of porcine small intestine and real teeth by using the proposed system

4 讨论与分析

本文提出了一种基于双目内窥镜的散斑三维重建系统，在双目内窥镜基线较窄的条件下，仍具有较高的测量精度和较好的重建效果。具体地，本文系统采用基于三维的标定优化方法实现了双目内窥镜系统的高精度标定，同时采用基于左右相机坐标轴旋转两次的极线校正方法，显著提高了左右图像共面行对齐的精度。本文提出的极线校正方法具有以下优势：

(1)双目内窥镜的两个摄像机绕坐标轴旋转同一个角度，以最小限度旋转就可具有相同的方向，这样使左右相机图像之间的特征差异最小化；

(2)校正后的图像与原始图像保持相同的分辨率，方便立体匹配，因为稠密匹配算法都需要相同大小的左右图像；

(3)最大化左右视图的公共视野，在校正后的图像中保证最大的可见图像面积，从而使校正过程中图像信息损失最小。

相较于传统标定方法[12]，本文提出的双目内窥镜系统通过对棋盘格提取角点拟合平面误差分析和对标准体进行精度测试，结果表明本文提出的双目内窥镜散斑系统在三维测量精度上具有较明显的优势。

由于双目内窥镜散斑系统真实应用在受限空间内，所以需要在保证高分辨率的情况下，将散斑光源缩小到双目内窥镜的探头上，而这对光学及材料提出了更高要求，需要进一步的研究。

5 结 论

本文基于立体视觉原理，搭建了一套基于散斑编码的双目内窥镜系统。为了提高系统的测量精度，本文着重针对双目内窥镜的标定和左右视图极线校正进行研究，提出了一种基于三维的非线性全局优化的标定方法和相机坐标轴旋转两次的极线校正算法。经过对棋盘格提取角点拟合平面的分析和对圆球、圆锥体及标准平面的精度测量，本文提出系统的测量精度相较于传统标定方法有显著提升。并且，对于实际应用场景中不同纹理对象目标的重建，如表面较为光滑的猪小肠内壁和纹理较少的且是非朗伯表面的高仿真牙齿，本文系统均取得了较好的重建效果。