坚固性系数与瓦斯放散初速度关联性探讨
李 凯,王 琳
(鹤壁职业技术学院,河南 鹤壁 458030)
煤与瓦斯突出严重制约了煤矿安全生产。煤与瓦斯突出发生条件复杂,发生机理尚未研究清楚,因此无法从根本上杜绝煤与瓦斯突出的发生。目前,对煤与瓦斯突出防治主要依靠基于综合假说所制定四位一体的综合防突措施,通过对煤与瓦斯突出案例调查分析发现,绝大多数突出事故发生都是因危险性预测失准而导致误采、误掘或者误揭突出危险煤体发生的,由此可见煤与瓦斯突出预测在防治突出过程中至关重要。
煤体坚固性系数f值与瓦斯放散初速度ΔP值为目前突出危险预测的两个常用重要指标,其中坚固性系数反映煤体自身强度大小,即抵抗突出发生能力的大小[1],而瓦斯放散初速度是反映煤体瓦斯放散能力的大小,即突出时突出能量源供应能力的大小[2],同时防突规定中还存在一个与两个指标密切相关的综合指标K值,它是由瓦斯放散初速度与坚固性系数比值。综合指标确定原则之一是用来确定综合指标的各个单项指标不能过多重叠,否则评价结果就会失真[3]。那么坚固性系数与瓦斯放散初速度之间关联性如何,综合指标K值的设置是否合理,有待进一步研究。
1 f值与ΔP影响因素分析
在前人研究成果基础上,将f值与ΔP影响因素分为两类:可控制因素与不可控制因素。可控制因素即可以人为改变的控制因素,主要是指标参数在测定过程中的一些人为限制条件,如f值测定过程中落锤次数、测煤粒径范围、测煤质量、捣筒高度、重锤质量等。ΔP的可控制因素包括:煤粒径、固定空间体积、温度、放散时间等。国标中对两个指标参数测定过程中各个可控因素都有明确规定,保证了f值与ΔP都是在各个相同实验条件下测定,这样使得两个指标各自之间普适性、对比性增加,为标准及临界值测定提供了基础,也为分析两者之间关系提供了可能。
不可控制因素,顾名思义指人为难以控制的影响因素,主要指煤体自身性质或成分的影响。近些年国内外相关学者做了大量实验研究,发现煤体变质程度[4-5]、破坏类型[6-8]、水分[9-10]、灰分[4]对f值与ΔP影响显著。变质程度越高、破坏程度越严重、煤体中水分灰分越高,煤体f值越小,ΔP越大。
2 f值与ΔP的相关性
2.1 f值与ΔP相关性分析
研究成果已证明煤坚固性系数及瓦斯放散初速度具有共同不可控影响因素,如破坏类型、煤变质程度、灰分、水分等。有学者研究表明煤比表面积与煤与瓦斯突出密切相关,即比表面积越大,瓦斯吸附量越高,瓦斯放散速度越高,突出危险性越高[11]。由此可知:煤的比表面积直接影响ΔP大小,而煤破坏类型、煤变质程度、灰分、水分等因素通过不同方式改变煤体的比表面积,进而间接影响ΔP的大小,其作用方式分别为:煤体破坏越严重,其内部孔裂隙发育越充分,主要为孔径小于100 nm微孔数量增加,进而比表面积增加;煤变质程度越高,煤体热挥发量越大,导致煤体内孔隙率增加,进而增加比表面积;煤中灰分致密性远大于煤体,灰分的增加造成煤分相对减小,煤比表面积增加;煤中水分会占据煤体表面上一定数量的吸附空位,同时水分能够造成裂隙堵塞,阻碍瓦斯的放散。
罗志明统计分析发现煤的坚固性系数f值与煤的孔隙有关,孔隙率越大,强度越小[12],但并未给出详细解释。笔者通过分析前人结果认为:煤的坚固性系数与煤体比表面积直接相关,煤体比表面积越大,煤体中自由面越大,当破碎功一定时,自由面越大煤体冲击破坏产生的新表面积就越多,产生小粒径煤粒也越多。根据f值计算公式,落锤次数一定条件下,0.5 mm以下煤粒越多,f值越小,那么,煤体破坏程度越严重、变质程度越高、水分、灰分越高,造成煤体比表面积增加,f测量值就会越小。这与前人统计分析结果是一致的。
水分与灰分除改变煤体比表面积外仍可通过其他方式改变f值与ΔP。水分增加可造成孔裂隙堵塞,导致ΔP减小,同时也会增加煤体塑形,造成f值增加。因灰分自身强度远大于煤体,灰分增加会造成f值增加。破坏类型及煤变质程度都是通过改变煤体内比表面积进而影响f值及ΔP大小,两者可由比表面积一个参量表示,由此各影响因素与两个指标之间关系如图1所示。从图1中可得,各个不可控因素与两个指标之间的关系是截然相反的,由此可推断f值与ΔP呈负相关关系。
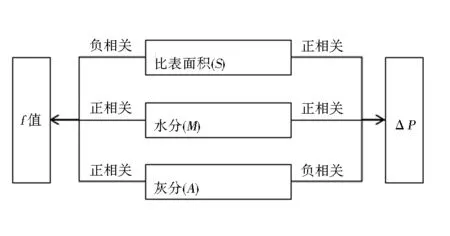
图1 不可控因素与f值与ΔΡ关系图
2.2 f值与ΔP统计分析
对全国30多个矿井的200多个煤样的坚固性系数及瓦斯放散初速度数据进行统计分析,发现其基本存在相同规律,因数据量较大,在此不一一列举,仅选择其中部分矿井数据进行分析。不同矿井煤样因物理成分、孔隙结构差别比较大,两指标间规律不明显,而同一矿井同一煤层其成分、孔隙往往相差不大,具有可比性,以下以矿为单位做两者关系图,见图2、图3、图4和图5。
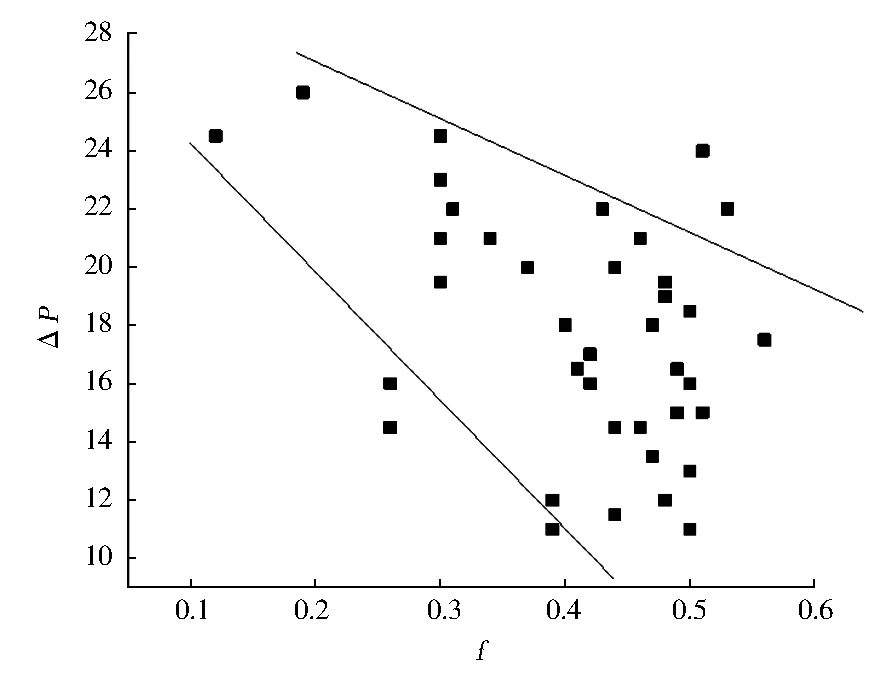
图2 阳泉煤矿3号煤层(无烟煤)
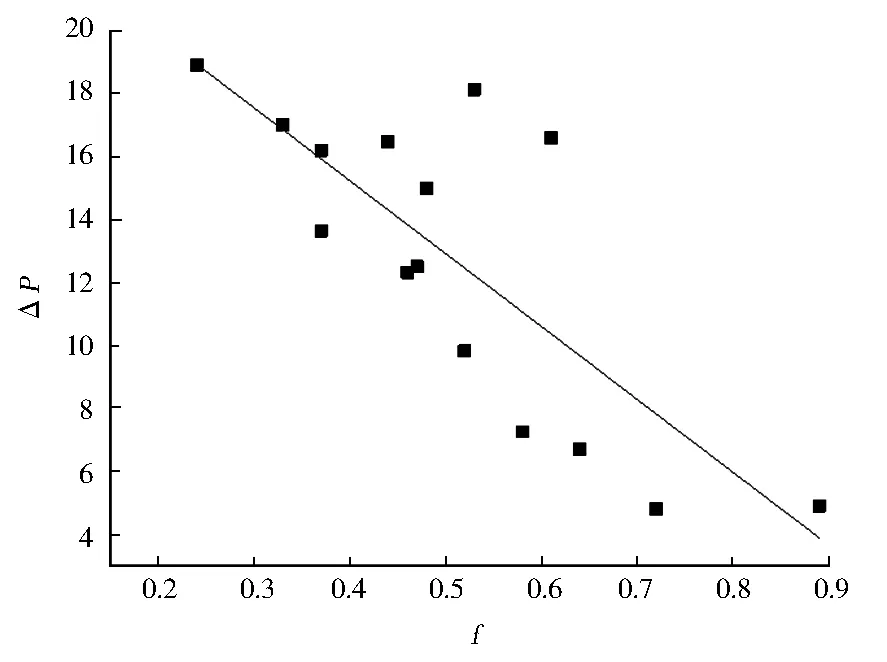
图3 薛庄村煤矿(贫瘦煤)
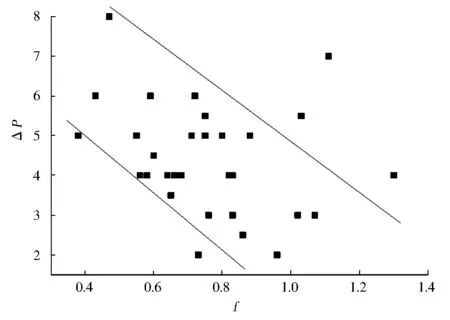
图4 丁集煤矿(焦煤)
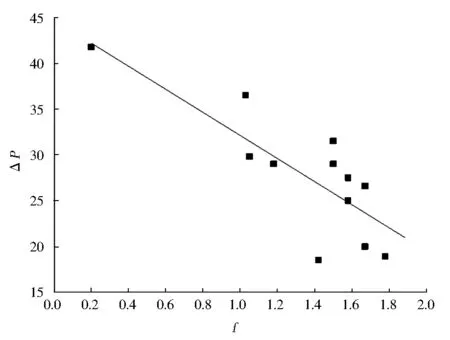
图5 临漳煤矿(无烟煤)
由图2、图3、图4和图5可得,不同矿井不同煤质的f值与ΔP呈现出相同规律性,即随着坚固性系数的增加瓦斯放散初速度呈减小趋势,这与前边分析结果是一致的。因参数测定过程Px即使煤样来自同一矿井同一煤层,因地质环境变化其成分差别依旧比较大,因此,个别矿井数据具有一定的离散性,但整体趋势依旧明显。
3 f值与ΔP预测模型建立及分析
根据以上分析结果,假设f值为一个由比表面积、水分、灰分共同决定的多元函数,即:
f=F1(S,M,A)
(1)
针对放散初速度,因灰分仍是通过改变煤体内比表面积而影响,即:
ΔP=F2(S,M)
(2)
由前文分析可知,各影响因素与f值与ΔP之间大致呈线性关系,由此假设:
f=a1S+a2M+a3A+a4
(3)
ΔP=b1S+b2M+b3
(4)
以九里山矿为例,计算公式(3)、公式(4)中各个系数值,并验证公式的正确性。九里山矿参数测定结果见表1,利用origin软件及九里山数据(前4个式样)进行多元回归分析,各系数回归结果见表2。
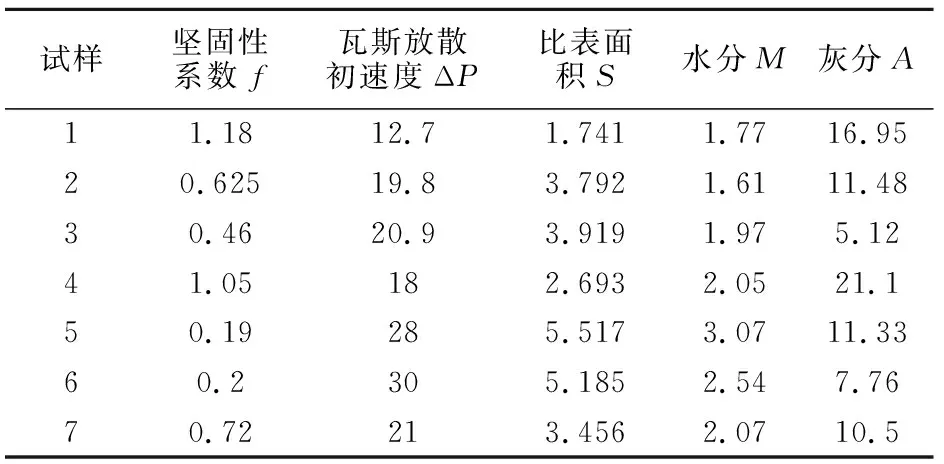
表1 九里山矿煤样基础参数

表2 各系数回归值
因比表面积与f值负相关,所以a1值理应为负,而水分、灰分与f值正相关,a2、a3值理应为正。同理,b1值应为正,b2值为负。系数回归结果发现,其中,a1、a3、b1与前边的分析结果是一致的,但水分却截然相反,分析其原因为比表面积对两个指标影响程度远大于水分对其影响,其覆盖了水分的影响作用。回归分析得到各个系数后,利用公式(3)和公式(4)对f值及ΔP进行预测,并分析其与真实值间误差,见表3。
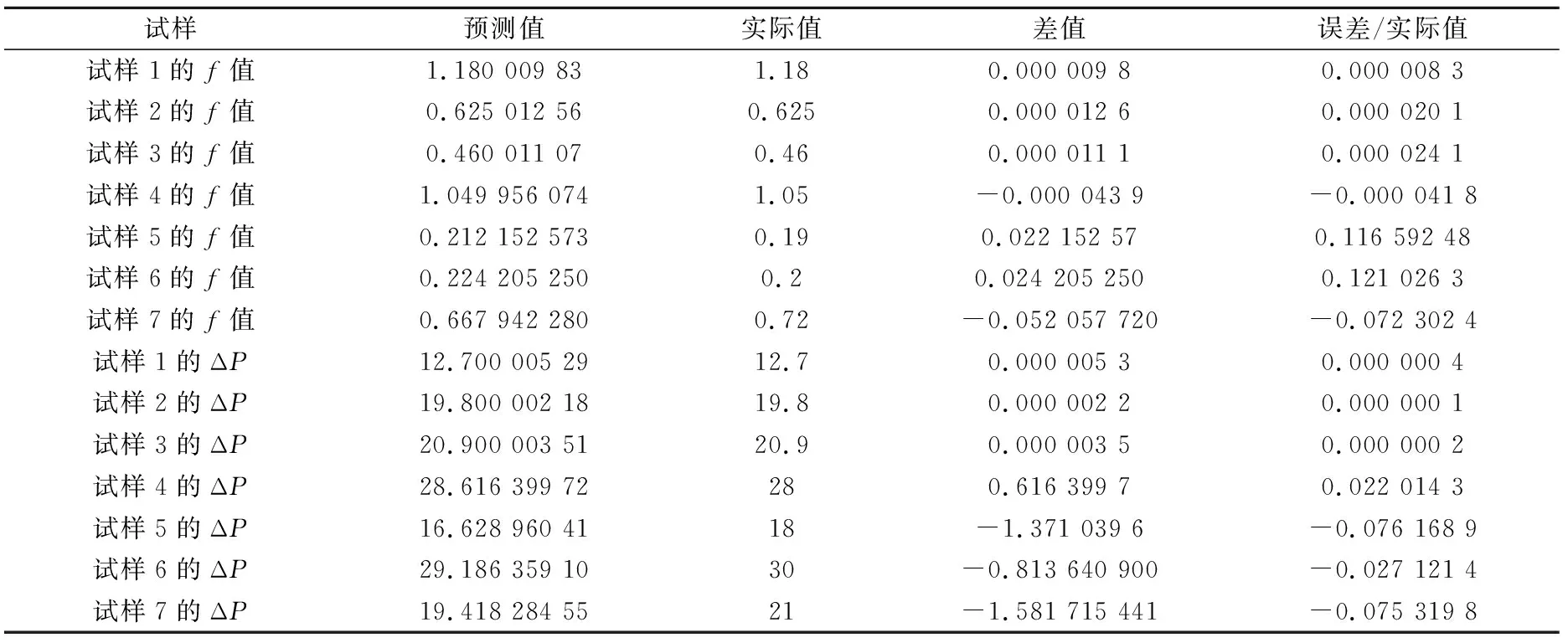
表3 误差分析
由表3可以看出:f值预测模型最大误差率为12.1%,ΔP预测模型最大误差率为7.6%,这说明模型是基本可靠的。
4 结 语
1)f值与ΔP受相同不可控因素影响,其分别为煤体破坏类型、变质程度、水分、灰分,各个影响因素都通过改变煤体比表面积大小来实现对f值与ΔP的控制。
2)f值与ΔP呈负相关关系,两者之间关系是通过其共同影响因素决定的,比表面积与f值负相关,与ΔP正相关;水分、灰分与f值正相关,与ΔP负相关。
3) 根据各个影响因素与f值、ΔP之间关系,分别建立两个指标预测模型,并验证了模型的可靠性。

