新型带自然对流散热末端的热泵系统性能分析
党鹏飞 马国远 许树学
(北京工业大学环境与生命学部 北京 100124)
0 引言
近年来,空气源热泵系统以其无污染、节能的优点得到了广泛的研究与应用。随着人们生活水平的不断提高,人们对室内舒适性的要求也越来越高[1]。分体式空调作为传统的供暖末端之一,具有对室内动态热负荷适应性强的能力,但其带来的吹风感、噪声、垂直温度梯度无法避免。许多学者将目光转向了一种无吹风感、无噪声、无垂直温度梯度的供暖系统,即带自然对流散热末端。许可[2]等对以地板供暖作为散热末端的空气源热泵进行了研究,提出了采用蓄热体蓄热的方法。S Rasoul Asaee[3]等提出将空气源热泵与散热器集合的系统,研究表明,该系统可减少36%的能源消耗和23%的温室气体排放。
上述系统均是制冷剂将热量传递给水,水再将这些热量传递给室内空气,二次换热型式一定程度上降低了空气源泵系统的能效。Shuxue Xu[4]等提出了一种以热管为散热器的空气源热泵(ASHPP)的概念,并进行了测试,结果表明ASHPP 系统的COP 可达4.35~4.64。邵索拉[5]等提出了一种使用新型蓄热型直接冷凝式加热板的空气源热泵供热系统,并进行了测试,结果表明,在室外空气温度为8℃时,系统COP 高达3.7。
针对现有空调末端强制对流带来的不适的吹风感,以及暖气片二次换热降低能效的问题,本课题组提出了一种利用自然对流进行散热的热泵系统[6]。该系统一方面可以减小中间换热损失,同时也使得系统更加简单可靠。本文针对此种带自然对流散热末端的热泵系统,并对该系统的运行特性进行了模拟分析,为后续试验提供参考。
1 系统原理
新型带自然对流散热末端的热泵系统装置如图1所示。热泵由压缩机、丝管式冷凝器、节流装置和蒸发器组成。工作过程为:从压缩机排出的高温高压制冷剂气体通过丝管式冷凝器,制冷剂冷凝放热并通过壁面与室内空气进行换热,冷凝后的制冷剂经节流装置节流后进入蒸发器,制冷剂在蒸发器中蒸发吸热,然后再回到压缩机,如此循环。制冷剂在丝管式冷凝器中是以自然对流和辐射的方式将热量传递给室内。
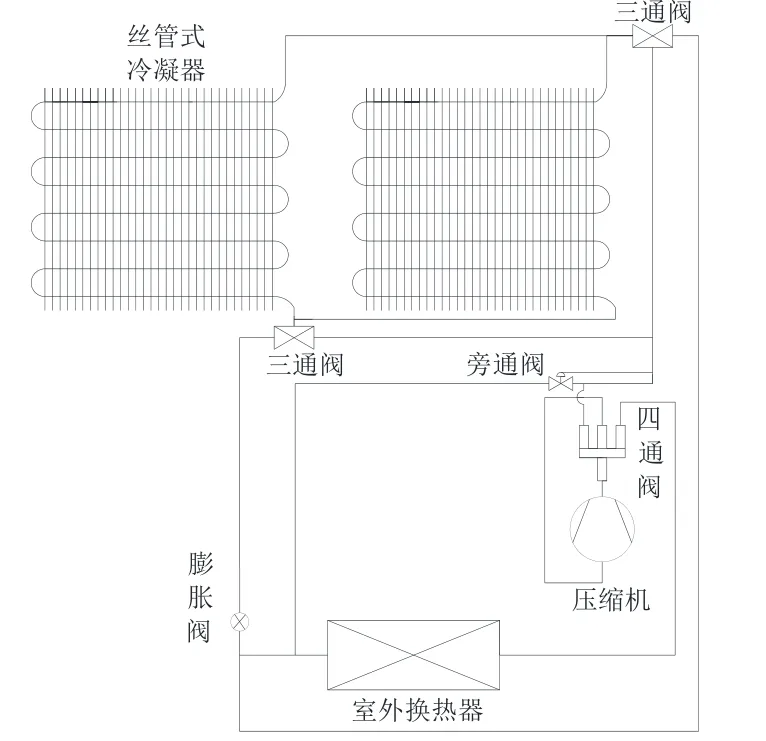
图1 带自然对流散热末端的热泵系统装置Fig.1 Heat pump system with natural convection heat dissipation end
2 传热过程与系统模型
2.1 热泵工作过程
制热量Q:

式中:G为制冷剂质量流量,kg/s;h进、h出分别为冷凝器进出口的焓值,kJ/kg。
制热COP:

式中:W为压缩机的输入功率,kW。
质量流量G:

式中:Vth为压缩机的容积输气量,m /h,vsuc为压缩机吸气口的制冷剂气体比容,m /kg,λ为容积效率。
2.2 冷凝器
假设:制冷剂在冷凝器中的流动为一维流动,不考虑压降;不考虑管壁的轴向换热;忽略管壁热阻;不考虑空气侧污垢的热阻。
(1)空气侧自然对流换热计算[7]:

式中:λa为空气热导率,W/(m·K);其定性温度tm为环境空气温度ta和壁面温度tw的平均值,tm=(t w+ta)/2。tw是冷凝管管壁温度;de为当量直径,m;Sb为蛇管相邻管间距,m;db为管外径,m;Sw为钢丝节距,m;dw为钢丝直径,m;Prf为空气的普朗特数,定性温度为tm,Grf为空气的格拉晓夫数,定性温度为tm。

式中:g为重力加速度,g=9.81m/s,β为空气在tm下的体积膨胀系数,1/℃,Δt为壁面温度tw与环境温度ta的温差,即Δt=t w-ta,v为在tm时空气的运动粘度,m /s。
当量直径de:

式中,ηf为肋片效率。肋片效率的变化并不大,一般可取0.85。
用于表示自然对流传热特征数的努塞尔数[8](Nusself)则为:

与自然对流相关的无量纲参数瑞利数(Rayleigh number)则为:

自然对流换热量为:
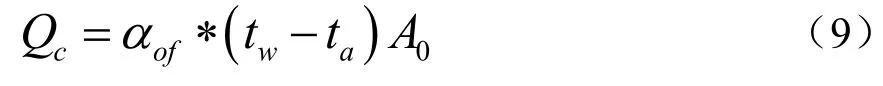
式中:A0为冷凝器外表面总有效换热面积,m 。
(2)空气侧辐射换热计算
由于此种新型散热末端空气侧自然对流系数较小,辐射换热占比重较大,因此通过辐射换热的热量不能忽略。根据辐射换热原理,可得冷凝器的辐射换热公式:
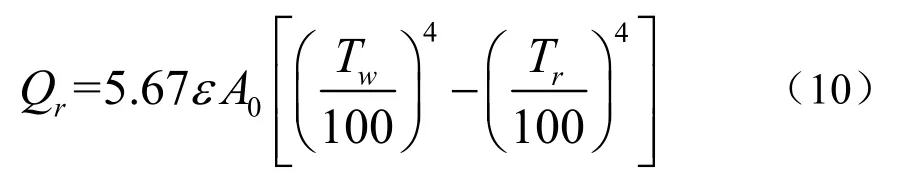
式中:ε为冷凝器外壁面的黑度,黑漆取0.95;A0为冷凝器外表面总有效换热面积,m ;Tw为冷凝器外壁面的平均温度,K;Tr为空气的平均温度,K。
将辐射换热量Qr写成与温差(t w-ta)有关的表达式,即:

(3)空气侧总换热过程
通过以上计算可以得到总换热量为:

(4)制冷剂侧换热
对于新型散热末端,其管内侧制冷剂与冷凝器内壁的换热与普通的水平管和竖直管均有较大差异,传统的换热公式对其并不适用。因此采用下式对制冷剂侧内换热系数进行计算:

与其对应的特征数的努塞尔数(Nusself)表示为:

普朗特(Prandtl)数则为:

雷诺(Reynolds)数则为:

式中:μref为制冷剂的动力粘度,kg/m·s;(Cp)ref为制冷剂的比热,J/kg·K。
3 模拟流程及模型验证
3.1 模拟流程
本文采用的新型散热末端的结构尺寸如表1所示。

表1 新型散热末端的主要结构尺寸Table 1 Main structural dimensions of new heat sink
使用文献[9]中提到的计算方法进行计算,计算流程图如图2所示,可知在额定工况下,假定制热量为9kW,冷凝器需要10.465m 的总换热面积,此时制冷剂可在冷凝器管道内充分冷凝,进而将热量传递到室内。由上表可求得,单片新型散热末端的换热面积为0.5075m,即选择新型散热末端21片最为适宜。

图2 计算流程图Fig.2 Calculation flow chart
参考标准《房间空气调节器》[10]中的工况本次对模型的计算采用以下参数作为计算条件:
(1)以室内空气温度18℃、20℃、22℃,室内末端壁面温度从25℃~50℃,间隔5℃进行计算。
(2)循环计算制冷剂选用R22,蒸发温度范围为-20℃~5℃,冷凝温度范围为25℃~45℃,过冷度及过热度均取5℃。压缩机选用某品牌涡旋压缩机,额定吸气量为7m /h、额定功率为2kW。
(3)压缩机指示效率、机械效率以及容积效率的选取参考样机[11]。
3.2 模型验证
为了验证该模型的可靠性,本文引用了文献[12]中的试验数据对模型进行验证,其对比图如图3所示,从图中可以看出,在较低的壁面温度下,文献中的实验值与数值模拟得到的模拟值的误差在8%,而在在较高的壁面温度下,文献中的实验值与数值模拟得到的模拟值的误差在1%,这表明了本文选用的数学模型的可靠性。

图3 不同壁面温度下散热量模拟值与实验值对比Fig.3 Comparison of simulated and experimental values of heat dissipation at different wall temperatures
4 模拟结果与分析
4.1 管内换热
根据上述模型,对制冷剂管内侧换热进行计算,其结果如表2所示。
由表2得出,在其他条件一定的情况下,随着冷凝温度的升高,管内侧换热系数逐渐降低。当冷凝温度为 25 ℃时, 换热系数最大为3122.72W/m ·K;当冷凝温度为45℃时,换热系数最小为2618.46W/m ·K。

表2 冷凝器管内侧换热计算结果Table 2 Calculation results of heat transfer inside condenser tube
4.2 管外换热
根据以上模型对新型散热末端在不同壁面温度、不同室温条件下,对流散热量与辐射散热分布规律进行分析。室内温度tin分别为18℃、20℃、22℃时,新型散热末端在壁面温度不同时,其自然对流散热量的变化如图4所示。由图可知,新型散热末端的自然对流散热量随着壁面温度的升高而增大。在壁面温度相同时,室内温度越低,丝管式冷凝器自然对流散热量越大。当室内温度从18℃升高至22℃时,自然对流散热量降低了15.59~65.69%。

图4 自然对流散热量变化规律Fig.4 Variation of natural convection heat transfer
室内温度tin分别为18℃、20℃、22℃时,在壁面温度不同时,新型散热末端辐射散热量的变化如图5所示。由图可知,新型散热末端的辐射散热量随着壁面温度的升高而增大。在壁面温度相同时,室内温度越低,新型散热末端辐射散热量越大。当室内温度从18℃升高至22℃时,辐射散热量降低10.84~56.27%。

图5 辐射散热量变化规律Fig5 The law of radiation heat dissipation
室内温度tin分别为18℃、20℃、22℃时,壁面温度不同时,新型散热末端总散热量的变化如图6所示。由图可知,新型散热末端的总散热量随着壁面温度的升高而增大。在壁面温度相同时,室内温度越低,新型散热末端总散热量越大。当室内温度从18℃升高至22℃时,总散热量降低13.64~61.22%。
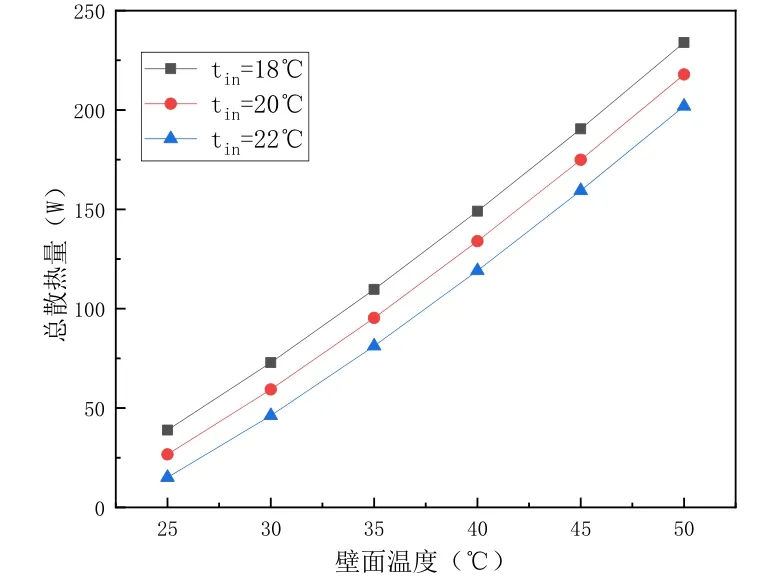
图6 总散热量变化规律Fig.6 Variation of total heat dissipation
在室内温度为18℃时,新型散热末端壁面温度在25~50℃变化期间,自然对流散热量与辐射散热量的关系如图7所示。

图7 散热量分配关系Fig.7 The relationship of heat dissipation distribution
在新型散热末端散热过程中,自然对流散热量与辐射散热量所占比例相差不大,自然对流散热量均高于辐射散热量。计算表明,自然对流散热量占总散热量的52.57-58.89%,辐射散热量占总散热量的41.11-47.43%。4.3 系统制热性能
系统在变工况下的理论制热量变化如图8所示。当蒸发温度te一定时,制热量随冷凝温度tk的升高而降低;当冷凝温度一定时,制热量随蒸发温度的升高而升高。在五个不同冷凝温度下,随着蒸发温度从-20℃升高至5℃,制热量升高了61.30~67.28%。在六组不同蒸发温度下,随着冷凝温度从25℃升高至45℃,制热量降低了12.84~26.00%。

图8 制热量变化关系Fig.8 The relationship of heating capacity change
理论功耗变化如图9所示。功耗随着冷凝温度tk的升高而升高。功耗不完全随冷凝温度的升高而升高,这是因为功耗与制冷剂循环流量、压缩机的机械效率以及指示功率的综合变化有关,而这些参数与冷凝温度的变化关系较复杂,从而导致各参数组合后出现此种情况。在六个不同蒸发温度下,随着冷凝温度从25℃升高至45℃,功耗升高了14.20~43.73%。

图9 功耗变化关系Fig.9 The relationship of power consumption variation
系统的COP 变化如图10 所示。当蒸发温度te一定时,其COP 随冷凝温度tk的升高而降低;当冷凝温度一定时,COP 随蒸发温度的升高而升高。在五组不同冷凝温度下,随着蒸发温度从-20℃升高至5℃,COP 升高了47.12~59.17%。在六组不同蒸发温度下,随着冷凝温度从25℃升高至45℃,COP 降低了36.50~50.97%。
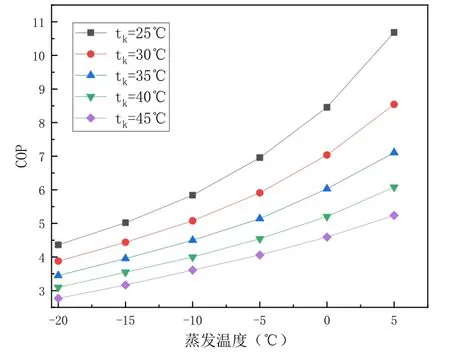
图10 COP 变化关系Fig.10 The relationship of COP change
制冷剂在冷凝器中需要将热量传递给壁面,然后冷凝器壁面与室内空气温度产生温差从而进行换热,因此冷凝器的散热量需要与压缩机的制热量相匹配。如图11 为压缩机的制热量与不同片数末端装置散热量的对比图。

图11 压缩机制热量与末端散热量匹配图Fig.11 Matching diagram of heat of compression mechanism and end heat dissipation
对于北京地区其供暖季的温度较低,低温可达到-10℃以下,室内温度会随室外温度降低而降低,此时所需冷凝温度偏高。由图11 可知,以蒸发温度-15℃,冷凝温度40℃~45℃时压缩机制热量为例,当末端为20 片时,其散热量的曲线与热泵制热量产生交点,这表明,热泵制热量可以很好的通过换热器散出,同时又能保证换热面积适当,不会出现成本过高的情况。这与上述设计计算一致。
5 结论
本文介绍了新型带自然对流散热末端的热泵系统的循环原理,针对北京地区冬季的气象条件,通过建立数学模型,研究了不同壁面温度、空气温度下,自然对流散热和辐射散热的分配规律,不同蒸发温度、冷凝温度下,各参数的变化规律,得到了以下结论:
(1)对于此种新型散热末端,其在不同冷凝温度下,管内侧换热系数不同,且随着冷凝温度的升高而降低。整体范围在2618~3123W/m ·K 之间。
(2)对于此种新型散热末端,其自然对流散热量占总散热量的52.57-58.89%,辐射散热量占总散热量的41.11-47.43%。自然对流散热量占比大于辐射散热量。
(3)对于此种新型散热末端的热泵系统,其制热量和COP 随蒸发温度的升高而升高,随冷凝温度的升高而降低。
(4)此种新型散热末端与压缩机制热量匹配较好的丝管式冷凝器片数为20 片。

