用于光纤F-P声压传感器的直流补偿解调技术研究

黄乐然，王 伟，王 震，董喜来，刘 彬*

（1.哈尔滨工程大学信息与通信工程学院，哈尔滨 150001；2.西安航天动力试验技术研究所，西安 710100；3.中电集团第49研究所，哈尔滨 150001）

1 引 言

非本征法布里－珀罗干涉（EFPI）光纤传感器具有灵敏度高、体积小、易复用、不受电磁干扰等优点，应用于航空、航天、石油工业和涡轮发动机等许多领域。在光纤F-P腔式传感器的测量系统中，解调技术是系统实现的关键，一般分为强度解调和相位解调两大类。相位解调的基本原理是通过测量F-P传感器的光谱信息，利用双波长算法、峰值检测等进行解算。相位解调可以得到FP腔的绝对腔长值，但是其算法相对较为复杂，且解调速度受到光谱测量硬件的影响。目前随着高速光谱采集设备和快速解调算法的发展，相位解调的速度正在提升，但仍然不适于高速动态信号的测量。强度解调技术则具有精度高、速度快、硬件成本低等优势，非常适宜在高速动态信号测量中的应用。常用的方法有正交工作点法、正交相移法等解调技术。正交工作点法需要可调谐光源以保证较高灵敏度，增加了系统硬件成本，且动态范围受限；而正交相移法需要保证入射光波长与腔长差精确匹配，这在试验中很难精确控制，进而导致解调精度不高。本文提出了一种应用于双腔EFPI传感器的直流补偿解调技术，腔长差可以不受限制。该算法通过一个固定波长的光源产生两个正交相移信号，采用DCM算法提取施加的动态信号，理论仿真和试验结果都证明了该方法的鲁棒性。

2 理论分析及数值模拟

2.1 双F-P腔结构理论分析

两个不同长度的F-P腔由两个标准单模光纤的劈裂面和声敏感膜片的内侧构成如图1所示。敏感膜片由PET材料制成，其内表面镀有金膜以提高反射率。两个空腔的长度分别为l和l，两条光纤之间的分离距离为h。

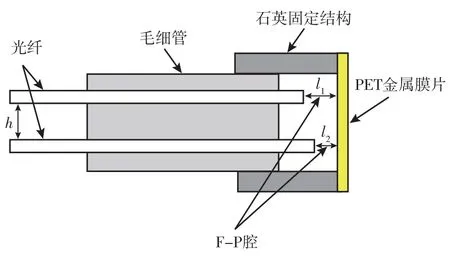
图1 EFPI传感器内部结构Fig.1 Internal structure of EFPI sensor

考虑到光纤端面的低反射率（约为3%），两个F-P腔都退化为双光束干涉仪，其干涉信号F可以写成

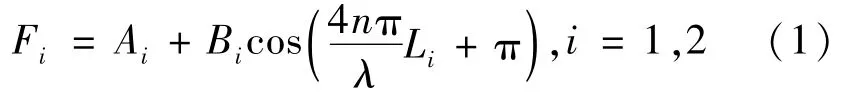
式中：A——干涉条纹的直流分量；B——干涉条纹的可见度；n——EFPI腔中介质的有效折射率，对于空气介质n＝1；L——F-P腔的长度；λ——入射光的波长。

当振膜由振动信号驱动时，腔长被调制为

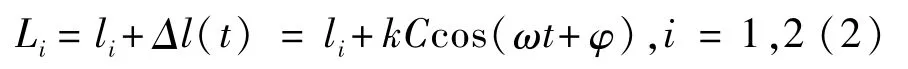
式中：l——F-P腔初始腔长；Δl（t）——声音信号引起的腔长变化量；k——传感器的灵敏度；C——声音信号的幅值；ω——声音信号的频率；φ——声音信号的初始相位。

根据双光束干涉原理，A和B可以表示为

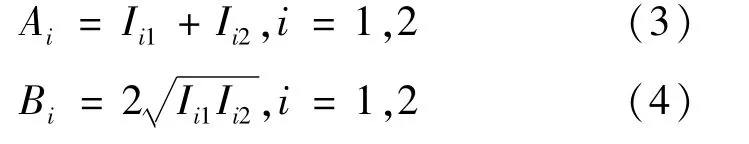
式中：I和I——分别是耦合到单模的两个光束经光纤和薄膜反射后的光强，I＝RI，I＝RI。其中，R——光纤端面的反射率；R——薄膜的有效反射率；I——入射光的光强。

根据公式（1）、（3）和（4），在消除直流分量后，这两个信号可以重写为

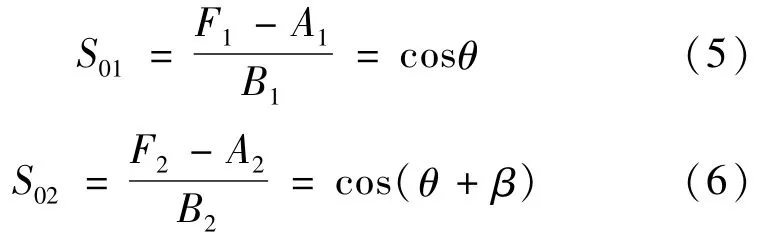
其中

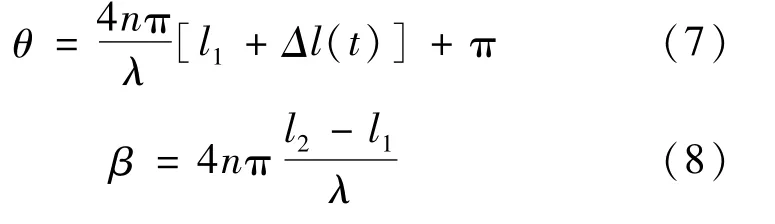
式中：S和S——分别为消除直流分量，归一化条纹对比度之后的两路信号；F和F——分别为两路干涉信号；θ——声音信号引起的相位变化量；β——F和F之间的初始相位差，对于给定的F-P腔差，是常数。

令a＝cosβ，b＝sinβ，

显然，S和S是两个正交相移信号。θ可通过DCM算法提取，由声音引起的腔长变化量可计算为

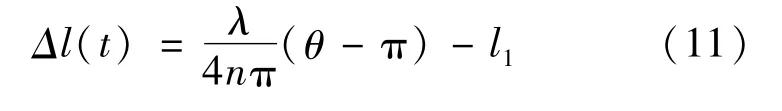
2.2 数值模拟分析

通过仿真验证了该方法的可行性，模拟参数见表1。在仿真过程中，所有采样频率均设置为512 kHz。

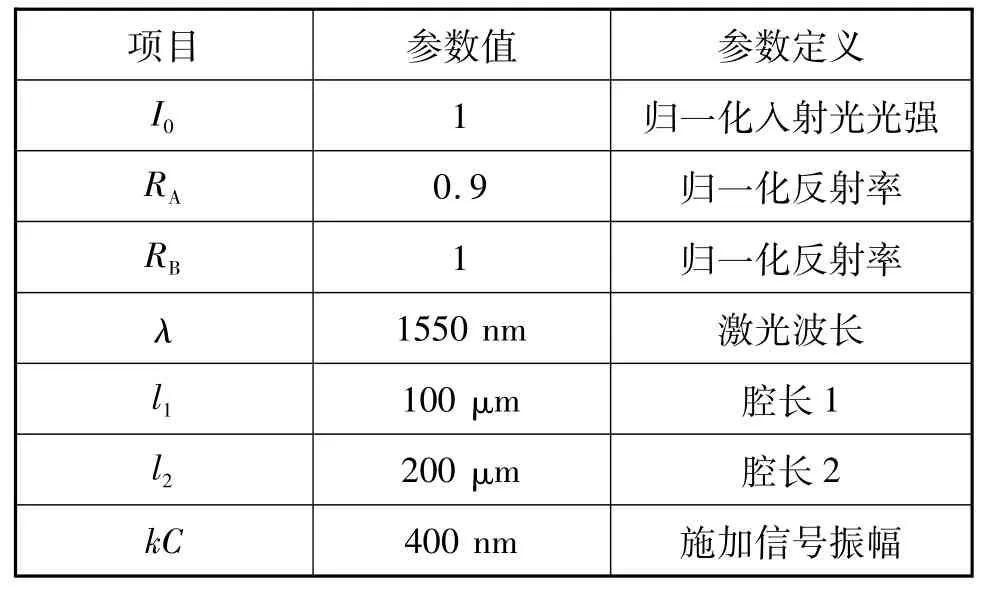
表1 模拟参数Tab.1 Simulation parameters

选择频率为5 kHz的声音信号进行仿真验证，获得的干涉信号F和F如图2（a）所示。结果表明，由于空腔变化较大，两者都发生了失真。图2（b）所示F和F的李萨如图。显然，李萨如图不是一个圆形，这表明两个信号不是正交的。图2（c）和（d）中所示的解调结果及其对应PSD与施加信号保持一致。

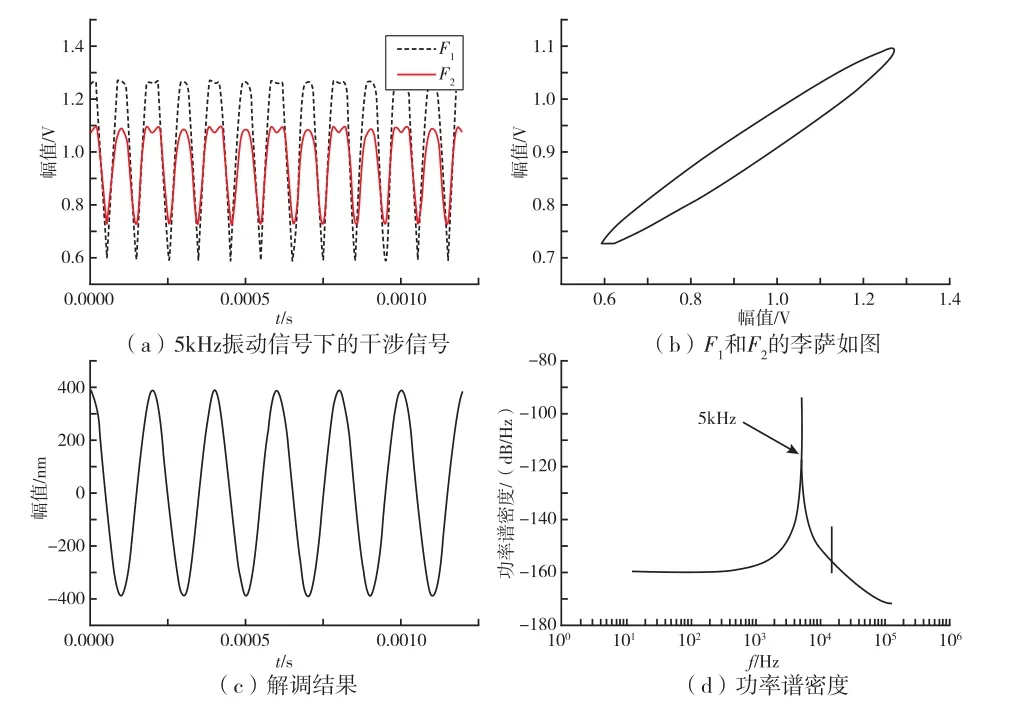
图2 EFPI传感器在5 kHz下的仿真结果Fig.2 Simulation results of EFPI sensor at 5 k Hz

3 试验结果及分析

3.1 双F-P腔传感器制作流程

对所提出的双F-P腔直流补偿解调算法进行试验验证。利用图3所示的工艺流程，制造了具有不同腔长差的EFPI光纤传感器。制作流程如下：

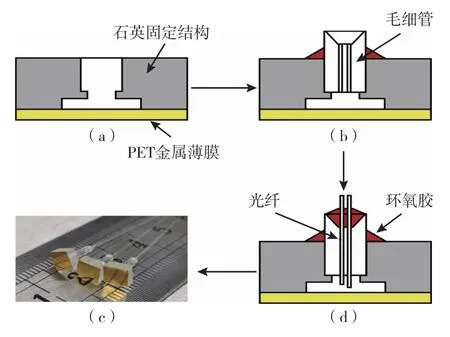
图3 双F-P腔EFPI传感器的制造过程Fig.3 Manufacturing process of dual F-P cavity EFPI sensor

（1）用环氧树脂胶将PET膜片连接到石英基底的表面，石英基底是通过传统的铣削工艺制造的；

（2）将带有两个通孔的毛细管插入石英基底的另一侧，其中较小的孔径与毛细管的直径相同；

（3）将两根光纤逐个插入孔中，并用环氧树脂胶密封，形成EFPI传感器。

图3（d）显示了制作的EFPI传感器的实物图。光谱由光谱分析仪（OSA）观察，以在制造过程中监测腔的长度。

图4显示了获得的F-P腔的归一化光谱。F-P腔长由λλ／（2（λ－λ））计算，其中λ和λ是每个频谱中相邻的波峰值或波谷值。EFPI传感器腔体参数见表2。

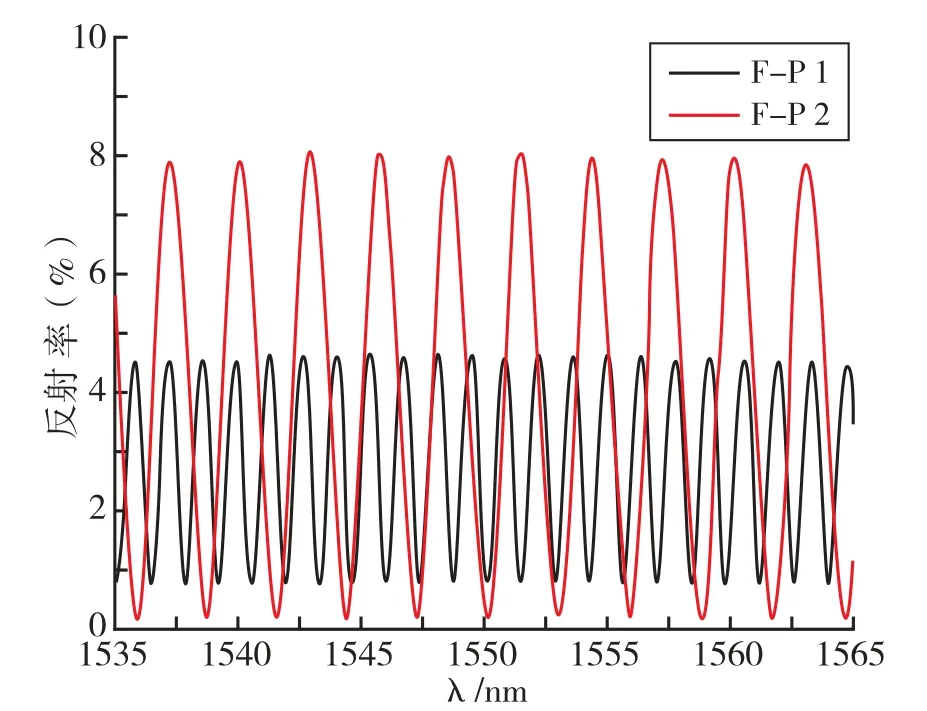
图4 EFPI传感器光谱Fig.4 EFPI sensor spectrum

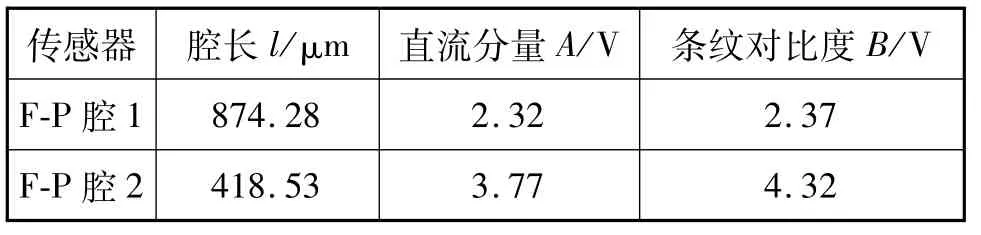
表2 EFPI传感器腔体的参数Tab.2 Parameters of EFPI sensor cavity

3.2 试验结果分析

光电测量系统由DFB窄带激光器、3 dB耦合器、环形器、EFPI传感器、光电探测器、数据采集卡和上位机构成，如图5所示。其中，DFB窄带激光器发出的激光中心波长为1550 nm，经过3 dB耦合器将光分为功率相近的两路光束，通过两路环形器将光入射到双F-P腔EFPI光纤传感器中，两路光信号用于探测一个光纤传感器的响应，然后由传感器反射回的反射光经过光电探测器将光信号转换为电信号，由数据采集卡采集得到样本数据，最终由上位机解调得出F-P腔腔长变化量，进而恢复出原始声信号。

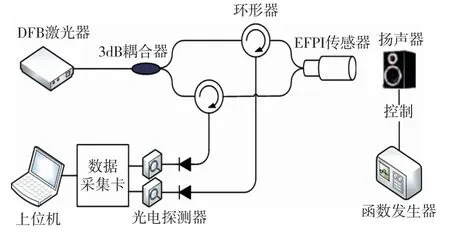
图5 光电测量系统Fig.5 Photoelectric measurement system

声源的加载方式采用函数发生器控制扬声器，以产生不同频率的声音信号。试验过程中，声源的位置距离传感器2 m处，且保证声波方向垂直于传感器入射，以保证较高的信噪比。利用光电测量系统，将频率为5 kHz的声波应用于传感器。

传感器采集到的干涉信号、李萨如图、解调信号和功率谱密度（PSD）如图6所示。两个F-P腔检测到的2 ms干涉信号如图6（a）所示，可以发现，信号明显受到了噪声干扰。两路信号的李萨如图如图（b）所示，显然，李萨如图并不是一个圆形，说明两路信号之间没有正交性。而李萨如图的实心性表明，这两路信号之间的相位差并不恒定。图6（c）为恢复出来的数据，在2 ms的时间区间内保持稳定。图6（d）显示了解调信号的功率谱密度（PSD），证明了解调信号的频率与声音的应用频率一致。

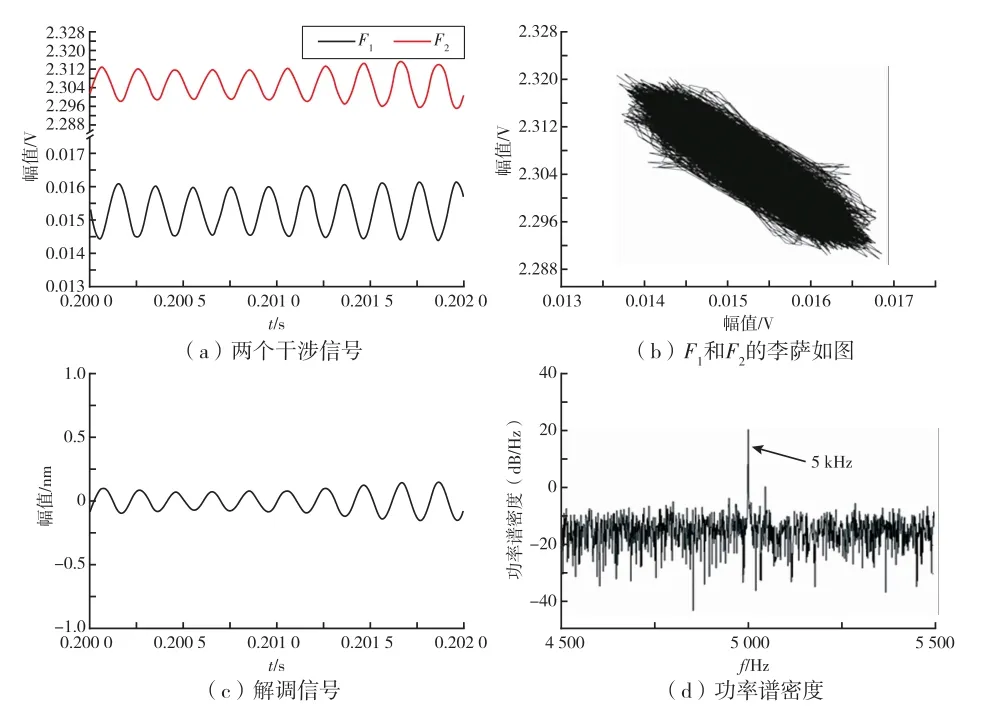
图6 EFPI传感器在5 k Hz下的试验结果Fig.6 Experimental results of EFPI sensor at 5 k Hz

考察传感器对不同频率的声压信号的恢复结果，对传感器施加500 Hz和1 kHz的声波，获得的信号和相应的解调结果如图7所示。从图7（a）、图7（c）中发现，解调结果发生失真，并不是标准的正弦信号，但其功率谱密度表明，解调结果与声音信号频率保持一致；而从图7（b）中不难看出，发生失真是由于有400 Hz等频率噪声的干扰导致的。试验过程中，这些噪声来源于光电探测器的电噪声以及传感器自身性能等。针对这些问题，后续试验会改进光电转换电路，进行滤波处理以消除电噪声影响，提高传感器耐高温、抗高压能力，以减小外界因素引起的腔长漂移对解调结果造成的影响。

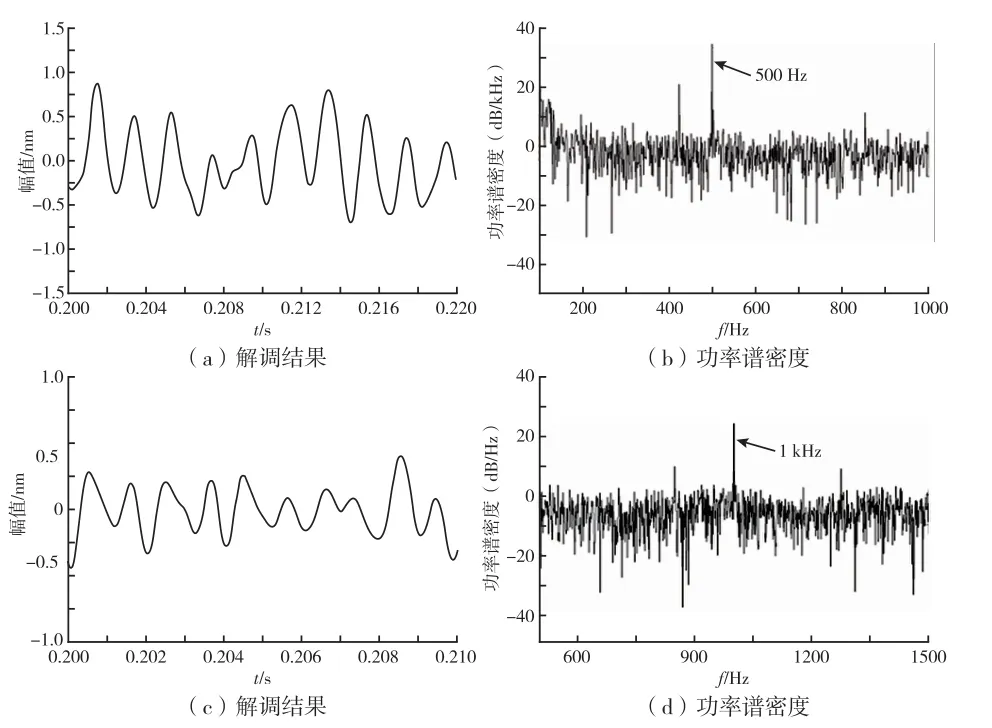
图7 EFPI传感器在不同频率声音信号下的试验结果Fig.7 Experimental results of EFPI sensor under different frequency sound signals

考察传感器对不同幅值的声压信号的恢复结果，对其施加声压从0.4 Pa～1.2 Pa的声波，获得的解调结果幅值如图8所示。从图8可以看出解调结果幅值与声信号的声压近似线性关系，该趋势线的拟合度R值为0.903 99，证明与趋势线的拟合程度较好。因此，该方法可用于不同幅值的声信号检测。

图8 传感器在不同声压下的恢复振幅Fig.8 Recovery amplitude of sensor under different sound pressure

4 结束语

针对具有双F-P腔结构的EFPI传感器的解调，本文提出了一种新的直流补偿技术，并对此进行了详细的理论研究和试验验证。该技术利用相同波长的激光入射两路具有不同腔长的F-P腔结构，来测量同一个动态信号；通过消除直流分量和进行信号校准，可以直接从测量得到的两路非正交信号中构造出两路正交信号，从而实现对被测信号的稳定恢复。研究结果表明，该技术无需将F-P腔的长度与光源的波长匹配。该解调技术具有速度快、动态范围大、不受腔长漂移影响、成本较低等优点，可用于EFPI传感器的复用。