一种惯性测姿装置的校准方法
肖小平,李永刚,何绪龙,赵功伟,董耀国,张俊杰
(1.湖南省计量检测研究院,长沙 410014;2.北京航天计量测试技术研究所,北京 100076)
1 引 言
惯性测姿装置是指应用力学中惯性原理构成的陀螺仪和加速度计等惯性仪表组成的姿态测量设备,被广泛应用于飞机、舰艇、火箭等运动载体的导航和控制系统中。随着科学技术尤其是电子技术、计算机技术和加工工艺的发展,陀螺仪和加速度计等仪表级惯性器件精度越来越高,惯性测姿装置的姿态测量精度也随之具有较大提升。
惯性测姿装置是导航和控制系统的关键部件,其性能的优劣直接影响运动载体的导航和控制精度,惯性测姿装置所引起的误差通常占整个导航系统误差的一半以上,因此,有必要对惯性测姿装置的姿态测量精度进行校准。
本文提出了一种校准方法,利用光学仪器测量手段对惯性测姿装置上立方镜的姿态角进行测量。根据测量结果,与惯性测姿装置输出的姿态角进行比较,得到姿态角误差,用于评价惯性测姿装置的姿态角测量精度,并对校准中产生的测量不确定度进行了评定。
2 惯性测姿装置原理及组成
惯性测姿装置利用三个相互正交的陀螺仪、加速度计建立载体坐标系,通过敏感地球自转角速度、载体加速度、重力加速度等参量,经过积分等算法解算出运动载体的姿态角和位置信息,从而为运动载体提供导航和控制信息。
惯性测姿装置包括主机和显控系统,主机里具有三个方向的陀螺仪、三向加速度计等传感器,陀螺仪与加速度计组合如图1所示。

图1 陀螺仪与加速度计组合Fig.1 Integration of gyroscopes and accelerometers
光学仪器测量是角度测量领域常用的高精度测量手段,通过传递外部方位角、安装水平传感器等方式建立姿态角标准。为了利用光学仪器对惯性测姿装置进行校准,需要在惯性测姿装置上安装立方镜,立方镜的姿态角能够表征惯性测姿装置输出姿态角。立方镜的工作面须经过超精密加工,确保工作面之间精确平行、垂直,每个工作面能够作为反光镜,如图2所示。为了全面考核惯性测姿装置的姿态角精度,校准时,可将惯性测姿置于不同的姿态,通过光学仪器测量进行校准。

图2 惯性测姿装置坐标定义Fig.2 Coordinate definition of inertial attitude measuring device
立方镜的M面和N面垂直,M面、N面与底面垂直。
坐标系定义:立方镜的M面法线指向为Y轴,N面法线的指向为X轴,依据右手定则,立方镜顶面法线为Z轴。
如图3所示,定义OXYZ为地理坐标系,X、Y、Z分别对应东、北、天方向。

图3 坐标转换中的姿态角Fig.3 Attitude angles in coordinate transform
从坐标系OXYZ到坐标系OXYZ的转换过程如下:
(1)绕Z轴转动角度φ,得到坐标系OXYZ,Y轴与Y轴夹角φ代表航向角;
(2)绕X轴转动角度θ,得到坐标系OXYZ,Y轴与Y轴夹角θ代表俯仰角;
(3)绕Y轴转动角度γ,得到坐标系OXYZ,X轴与Y轴指向与水平面的夹角代表滚动角。
依据右手坐标系定则,惯性测姿装置输出姿态角的欧拉方程表达式为

3 姿态角的校准方法
惯性测姿装置姿态角校准包括方位角的校准、俯仰角的校准和滚动角的校准,下面将分别详述各参数的校准方法。
惯性测姿装置姿态角的校准需要采用的设备为天文点和电子经纬仪。其中方位角标准采用一等天文点,根据相关标准,一等天文点的方位角误差为0.5″,天文点上具有能够表达其方位角的标准镜。电子经纬仪的精度等级为Ⅰ等,根据相关标准,Ⅰ等电子经纬仪的水平测角误差0.5″,竖直测角误差0.5″,水平补偿器补偿误差3″。
3.1 方位角校准方法
方位角的校准利用天文点作为方位角标准,利用电子经纬仪作为角度传递设备。
将惯性测姿装置和校准设备放在具有一等天文点的实验室内,天文点上方位标准镜的大地方位角为A。将惯性测姿装置安放在一个稳定工作台上,如图4所示。

图4 惯性测姿装置方位角校准示意图Fig.4 Azimuth angle calibration of inertial attitude measuring device
在方位标准镜正前方架设电子经纬仪A,调整电子经纬仪A的位置,确保能对方位标准镜自准直测量;在惯性测姿装置立方镜M面正前方架设电子经纬仪B,确保能对准立方镜M面自准直测量,且电子经纬仪A和电子经纬仪B之间能够通视无遮挡,测量前,通过观察水平补偿器将电子经纬仪A和电子经纬仪B调平。准备完成后,将惯性测姿装置加电开机。
电子经纬仪A对方位标准镜自准直时,电子经纬仪A的目视分划板与准直分划板返回像对齐,记录电子经纬仪A水平盘读数值H,然后将电子经纬仪A与电子经纬仪B对瞄,记录电子经纬仪A水平盘读数值H,电子经纬仪A水平测角值的计算公式为

电子经纬仪B与电子经纬仪A对瞄时,电子经纬仪B的目视分划板与电子经纬仪A准直分划板对齐,记录经纬仪水平盘读数值H,然后将电子经纬仪B对准立方镜M面自准直,记录经纬仪水平盘读数值H,电子经纬仪B水平测角值的计算公式为

校准设备得到的惯性测姿装置方位角的计算公式为

可见,通过校准设备的测量,获取惯性测姿装置的航向角φ,作为惯性测姿装置方位角的真值。
惯性测姿装置工作中输出方位角φ,惯性测姿装置方位角的误差的计算公式为

其计算结果即为惯性测姿装置方位角的校准误差值。
3.2 俯仰角校准方法
根据惯性测姿装置俯仰角的定义,立方镜Y轴的俯仰角即为装置的俯仰角。Y轴方向与M面法线一致,惯性测姿装置的俯仰角可以通过电子经纬仪测量M面直接获取。
该校准方法是利用电子经纬仪的水平补偿器作为水平标准,通过竖直测盘读数作为俯仰角进行校准。为了消除电子经纬仪水平补偿器的水平误差和轴系误差,测量时对电子经纬仪进行正倒镜两次读数。校准方法如下:
(1)利用图5所示的方式摆放惯性测姿装置和电子经纬仪A,调整三脚架将电子经纬仪A的望远镜对准立方镜的M面,使经纬仪能够对M面自准直测量,记录经纬仪竖直盘读数值V;
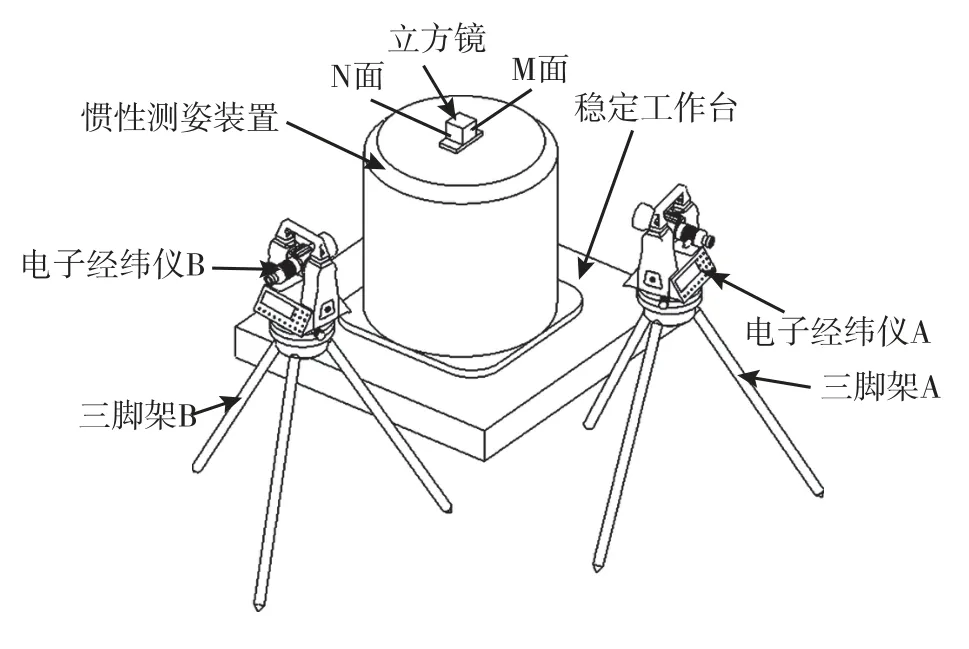
图5 惯性测姿装置俯仰角和滚动角校准示意图Fig.5 Pitch angle and roll angle calibration of inertial attitude measuring device
(2)将电子经纬仪A倒镜,对准立方镜M面自准直测量,记录经纬仪竖直盘读数值V。
依据右手定则,通过校准设备获得惯性测姿装置的俯仰角θ计算公式为

θ作为惯性测姿装置俯仰角的真值,惯性测姿装置工作中输出俯仰角θ。
惯性测姿装置的俯仰角误差的计算公式为

其计算结果即为惯性测姿装置俯仰角的校准误差值。
3.3 滚动角校准方法
依据滚动角的定义,滚动角为绕Y轴转动的角度值,立方镜坐标系中X轴的指向不能代表滚动角,不能直接利用电子经纬仪进行测量。由于滚动角为空间坐标系的参数,可以通过计算获得。校准方法如下:
如图5所示,将电子经纬仪B对准立方镜N面自准直测量。首先利用水平补偿器将电子经纬仪B整平,电子经纬仪B望远镜对立方镜N面自准直测量,电子经纬仪B的目视分划板与准直分划板返回像对齐,读取经纬仪竖直盘读数值V。为了消除仪器水平度和轴系误差,将电子经纬仪B倒镜,对准立方镜N面进行自准直测量,记录经纬仪竖直盘读数值V。
通过外测得到的立方镜N面法线的俯仰角计算公式为
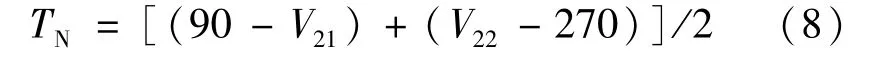
为了求解立方镜的滚动角γ,简化计算,假设立方镜的航向角为φ=0,已知俯仰角为θ。姿态矩阵简化为

对于立方镜,N面与M面垂直,假设为N面相对于M面绕Z轴旋转了-90°,如图6所示,绕Z轴的旋转矩阵为

图6 坐标系旋转示意图Fig.6 Rotation of coordinate system

旋转后的矩阵方程为

将公式(9)和公式(10)代入公式(11),得

假设立方镜Y轴与X轴重合,指向为方位角φ,那么通过电子经纬仪B测量获得的倾角T,代表Y轴的俯仰角。
姿态角的欧拉方程为

令C[3,2]=C[3,2],求解矩阵方程,惯性测姿装置的滚动角γ计算公式为

γ作为惯性测姿装置滚动角的真值,惯性测姿装置工作中输出滚动角γ。
惯性测姿装置的滚动角误差计算公式为

其计算结果即为惯性测姿装置滚动角的校准误差值。
4 姿态角校准试验
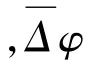

表1 方位角校准试验数据Tab.1 Azimuth angle calibration test data

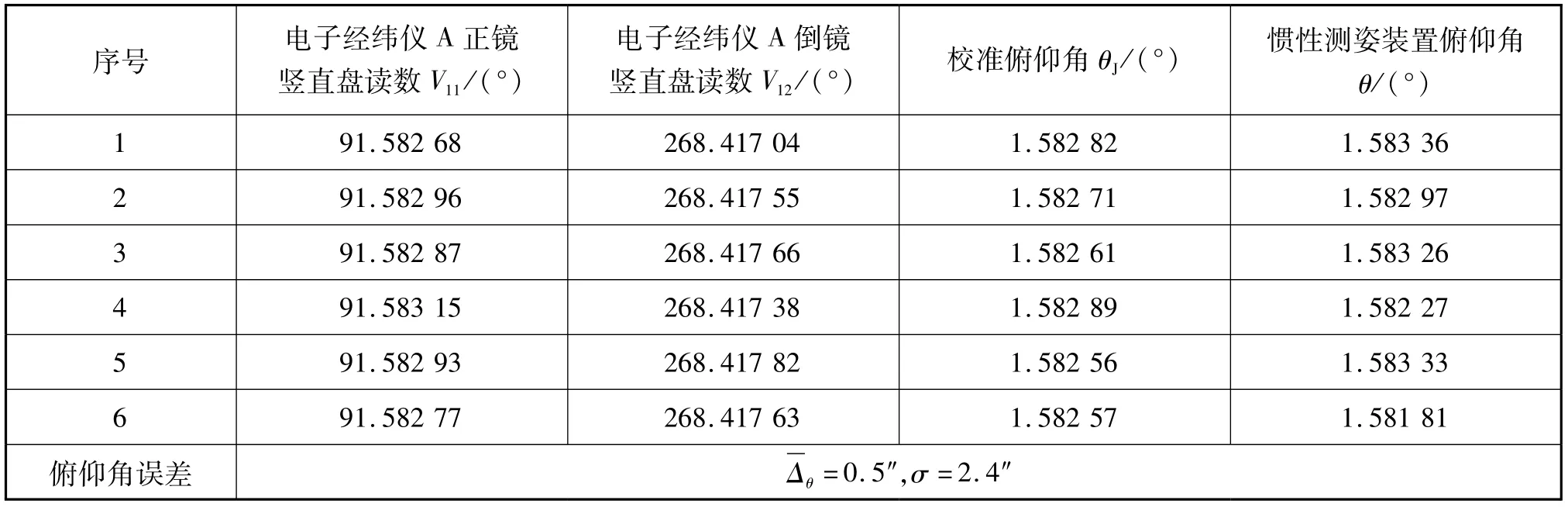
表2 俯仰角校准试验数据Tab.2 Pitch angle calibration test data


表3 滚动角校准试验数据Tab.3 Pitch angle calibration test data
通过对以上校准数据进行数据处理,获得姿态角的误差在合理范围,说明本文提出的校准方法可行。
5 测量不确定度评定
惯性测姿装置的校准参数主要包括方位角、俯仰角和滚动角,下面分别针对三个参数分别进行测量不确定度评定。
5.1 方位角的测量不确定度评定
方位角的测量不确定度分量主要包括:天文点标准镜方位角误差引入的测量不确定度u(A)、电子经纬仪A水平测角引入的标准不确定度分量u(α),电子经纬仪B水平测角引入的标准不确定度分量u(α)。


根据公式(4),灵敏系数c=1,c=1,c=1。
5.1.1 天文点方位角误差引入的测量不确定度分量u(A)


5.1.2 电子经纬仪A水平测角引入的标准不确定度分量u(α)
(1)电子经纬仪A水平测角重复性引入的标准不确定度分量u(α)。
在相同条件下,利用电子经纬仪A对固定角度进行6次测量,6次测量数据见表1,按公式(2)计算电子经纬仪A水平测角值α,按照贝塞尔公式(17)计算其重复性s为

式中:n——测量次数;i——测量次序,i=1…n。
电子经纬仪A水平测角重复性计算结果为
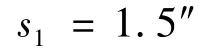
电子经纬仪A水平测角重复性引入的标准不确定度分量可用A类评定方法计算为

(2)电子经纬仪A水平测角误差引入的标准不确定度分量u(α)。

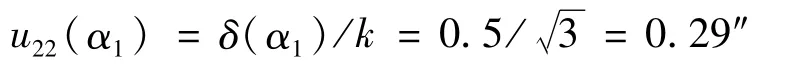
(3)电子经纬仪A水平测角引入的标准不确定度分量u(α)。
测量过程中,电子经纬仪A使用两次,那么其水平测角引入的标准不确定度分量为

5.1.3 电子经纬仪B水平测角引入的标准不确定度分量u(α)
(1)电子经纬仪B测角重复性引入的标准不确定度分量u(α)。
在相同条件下,利用电子经纬仪B对固定角度进行6次测量,6次测量数据见表1,按公式(3)计算电子经纬仪B水平测角值α,按照贝塞尔公式(18)计算其重复性s为

电子经纬仪B水平测角重复性计算结果为

电子经纬仪B测角重复性引入的标准不确定度分量可用A类评定方法计算为

(2)电子经纬仪B水平测角误差引入的标准不确定度分量u(α)。
电子经纬仪B经过检定合格,即水平测角误差δ(α)=0.5″,电子经纬仪B水平测角误差引入的标准不确定度分量为

(3)电子经纬仪B水平测角引入的标准不确定度分量u(α)。
测量过程中,电子经纬仪B使用两次,那么其水平测角引入的标准不确定度分量为

合成标准不确定度u按公式(17)计算。

合成标准不确定度为

工程应用中,取k=2,其置信水平约为0.95,则扩展不确定度U为

5.2 俯仰角的测量不确定度评定
俯仰角的测量为直接测量,引起俯仰角的测量不确定度包括电子经纬仪A正镜测量引入的标准不确定度分量u(V)、电子经纬仪A倒镜测量引入的标准不确定度分量u(V)。


根据公式(6),灵敏系数c=0.5,c=0.5。
5.2.1 电子经纬仪A正镜测量引入的标准不确定度分量u(V)
(1)电子经纬仪A正镜时竖直测角重复性引入的标准不确定度分量u(V)。
利用电子经纬仪A对惯性测姿装置立方镜进行6次正镜测量,6次测量数据见表2,按照贝塞尔公式(21)计算其重复性s。

电子经纬仪A竖直测角重复性计算结果为

电子经纬仪A正镜竖直测角重复性引入的标准不确定度分量可用A类评定方法计算,为

(2)电子经纬仪A正镜时竖直测角误差引入的标准不确定度分量u(V)。


(3)电子经纬仪A正镜测量引入的标准不确定度分量为

5.2.2 电子经纬仪A倒镜测量引入的标准不确定度分量u(V)
(1)电子经纬仪A倒镜竖直测角重复性引入的标准不确定度分量u(V)。
利用电子经纬仪A对惯性测姿装置立方镜进行6次倒镜测量,6次测量数据见表2,采用5.2.1节贝塞尔公式计算方法,电子经纬仪A进行6次倒镜测量,测量重复性s=0.83″。电子经纬仪A倒镜竖直测角重复性引入的标准不确定度分量为

(2)同正镜测量,电子经纬仪A倒镜时竖直测角误差引入的标准不确定度分量u(V)为
u(V)=0.29″
(3)电子经纬仪B倒镜测量引入的标准不确定度分量:

合成标准不确定度u按公式(22)计算。

合成标准不确定度为

工程应用中,取k=2,其置信水平约为0.95,则扩展不确定度U为
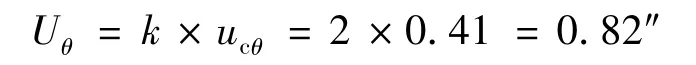
5.3 滚动角的测量不确定度评定
滚动角的测量为间接测量,根据滚动角计算公式(14)。


根据公式(14)和表3滚动角校准数据,对滚动角测量不确定度的影响量主要是立方镜N面法线的倾角T,即灵敏系数c≈1,c≈0,公式(23)可简化为

引起立方镜N面法线倾角T的测量不确定度包括电子经纬仪B正镜测量引入的标准不确定度分量u(V),电子经纬仪B倒镜测量引入的标准不确定度分量u(V)。
采用第5.2条相同的计算方式,依据表3滚动角校准数据,对滚动角的测量不确定度进行分析。
5.3.1 电子经纬仪B正镜测量引入的标准不确定度分量u(V)
(1)电子经纬仪B正镜竖直测角重复性引入的标准不确定度分量u(V)。
利用电子经纬仪B对惯性测姿装置立方镜进行6次正镜测量,6次测量数据见表3,采用5.2节贝塞尔公式计算方法,电子经纬仪B进行6次正镜测量,测量重复性s=0.69″。电子经纬仪B正镜竖直测角重复性引入的标准不确定度分量为

(2)电子经纬仪B正镜时竖直测角误差引入的标准不确定度分量u(V)

(3)电子经纬仪B正镜测量引入的标准不确定度分量
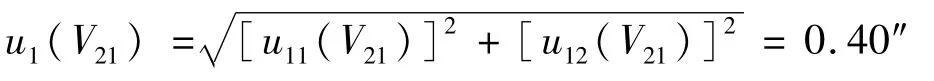
5.3.2 电子经纬仪B倒镜测量引入的标准不确定度分量u(V)。
(1)电子经纬仪B倒镜时竖直测角重复性引入的标准不确定度分量u(V)
利用电子经纬仪B对惯性测姿装置立方镜进行6次倒镜测量,6次测量数据见表3,采用5.2节贝塞尔公式计算方法,电子经纬仪B进行6次倒镜测量,测量重复性s=0.76″。电子经纬仪B倒镜竖直测角重复性引入的标准不确定度分量为

(2)同正镜测量,电子经纬仪B倒镜时竖直测角误差引入的标准不确定度分量u(V)为

(3)电子经纬仪B倒镜测量引入的标准不确定度分量

电子经纬仪B测量引起的标准不确定度u(T)按公式(22)计算

将不确定度分量代入公式(23),获得
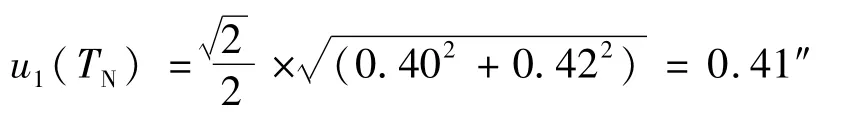
根据公式(24),合成标准不确定度为

工程应用中,取k=2,其置信水平约为0.95,则扩展不确定度U为
U=k×u=2×0.41=0.82″
5.4 结论
经试验验证,惯性测姿装置校准结果的测量不确定度评定结果合理,测量不确定度评定方法可行,满足惯性测姿装置姿态角的校准要求。
6 结束语
本文介绍了一种利用光学仪器对惯性测姿装置姿态角的校准方法,同时对校准设备的测量不确定度进行了评定,通过试验证明该方法可行,解决了惯性测姿装置高精度校准的难题。该方法也可推广应用于其它设备姿态角的校准。

