一种同质传感器的最优加权融合算法研究

郑良骏，杨金鑫，王志明

(南京理工大学机械工程学院，江苏南京 210000)

0 引言

同质传感器数据融合应用广泛，如环境监测[1]和农业生产[2]、工业生产[3]。采用数据融合，能减小被测对象的不确定性，从而提高检测及监控的准确度和可靠性。因此许多学者对同质传感器数据融合算法进行了深入研究。丁浩晗等使用最小二乘法滤波，再使用改进权值动态分配算法提高了船舶的动力定位精度[4]；许可等使用BP神经网络进行缺失数据补全，再使用分批估计的自适应加权算法进行数据融合,避免了样本量过大产生的方差值僵化问题[5]；曹守启等使用隶属函数剔除粗大误差，再使用分批估计和自适应加权融合算法采集环境温度[6]；朱聪通过设计的空间和时间一致性指标剔除异常数据，采用区域殇捕获特征数据，再根据特征位置和传感器空间关系定义约束条件，得出可信度，以可信度为权值融合数据[7]；李红等综合自适应加权融合算法和基于B型关联度的加权融合算法，对两种算法各自得到的加权因子再次分配权值度，进行融合[8]。

以上算法都属于二级融合算法，先对单一传感器采集的数据进行预处理，再使用加权融合算法对数据进行融合。但是其算法复杂，效率不高，针对此问题对数据预处理算法进行改进，并与传统与处理算法比较，结果表明，改进算法对粗大误差的剔除更准确，效率更高，可使数据融合结果的标准差更小。

1 数据融合算法处理过程

1.1 数据预处理

在实际的传感器测量中，往往会在短时间内用同一传感器对同一物理量进行重复测量，得到多个原始数据以供处理，避免测量的偶然性。然而，由于传感器自身特性、电路问题、环境干扰及其他因素的影响，导致单一传感器测量到的原始数据对于真实值有较大偏差。因此需要对原始数据进行预处理，主要是剔除粗大误差。数据量较少时，常用格拉布斯准则和狄克逊准则。

狄克逊准则的做法如下：首先将得到的一组测量数据从小到大依次排列得到数组x1,x2,…，xn，其中xn为最大值，x1为最小值，然后根据n的大小来进行不同的计算，得到统计量β和β′。

n=3～7时：

(1)

n=8～10时：

(2)

n=11～13时：

(3)

规定D(n,α)为狄克逊判定准则临界值，其中n为测量次数，α为显著水平，α可以取0.01或0.05，表1为摘取的部分n和α对应的D值。

表1 狄克逊判定准则临界值

判断准则为：当β>β′且β>D(n,α)时，则认为xn为异常值，当β<β′且β>D(n,α)时，认为x1为异常值。判断并剔除了一个异常值后，对剩余的数组重新计算统计量并进行下一次判断。

1.2 最优加权融合算法

最优加权融合算法，无需传感器测量数据的任何先验知识，即可融合出方差的最小数据融合值。

(4)

总均方误差为

(5)

由式(5)可知，当总均方误差最小时，对应的权值为

(6)

此时对应最小的总均方误差为

(7)

由式(7)可知，最优权值与各传感器的方差有关。

1.3 改进数据预处理算法

如果使用最优加权融合算法来对同质传感器的数据进行融合，为了使得最终融合结果的总均方误差最小，需要降低各组数据的方差，因此可以对数据预处理部分的算法进行改进，使其可准确剔除粗大误差，减小各组数据方差。

改进算法原理：传感器测量的数据=真实值+噪声。噪声符合期望为零的正态分布，当对同一物理量有足够多的测量数据时，数据的分布应该近似于正态分布，其均值=期望，期望≈数据的中值。但由于测量数据有时不足，根据公式求得的期望与方差会被粗大误差影响。因此使用中值代替均值，使用估计标准差代替实际标准差，根据3sigma准则来剔除粗大误差。

改进算法具体步骤如下：测量得到一组数据，从小到大排列为x1,x2，…，xn-1，xn，设为集合U，其中xn为集合最大值，x1为集合最小值，设数组中值为xmed。其中：

(8)

取xmed及其左侧数据为集合A，取xmed及其右侧数据为集合B，再取集合A的中值xAmed与集合B的中值xBmed。

假设后续数据测量值均匀分布在x1与xn之间。以集合A为例，则某一测量数据xj落在xmed与xAmed之间的概率为25%。有下式：

(9)

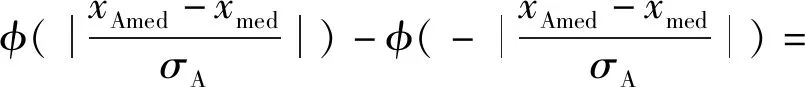
(10)

(11)

(12)

式中：X～N(0,1)；σA为估计标准差；μ为期望；φ(x)为标准正态分布的分布函数。

查取标准正态分布分位数表，可得：φ-1(3/4)=0.674 489,则根据式(12)得σA=|xAmed-xmed|×1.482 6，剔除集合U中小于xmed-3σA的值。对于集合B，求取集合B的估计标准差σB，剔除集合U中大于xmed+3σB的值。算出预处理后集合U的平均值和标准差，代入最优加权算法进行数据融合。

2 各算法处理结果比较及分析

2.1 数据来源

为了对比各算法对粗大误差剔除的效率和准确度,使用多个一氧化碳传感器与相关实验设备测得数组某时段一氧化碳浓度数据。对待处理数据进行处理，进而实现各算法的验证与比较，测得一氧化碳原始数据见表2(1 ppm=10-6)。

表2 某时段待融合一氧化碳数据 ppm

该组数据中有5组数据,将其从大至小排列后，分别引入不同类型的粗大误差，A1数据引入1个极大粗大误差，A2数据引入2个极大粗大误差，A3数据引入2个极大粗大误差与1个极小粗大误差，A4数据引入1个极小粗大误差与极大粗大误差，A5组数据保持不变。其中极大极小粗大误差分别在原有最大或最小数据上增加或减少5%，处理后数据见表3。

表3 引入粗大误差的待处理一氧化碳数据 ppm

2.2 结果分析对比

以标准差σ作为评价标准，分别使用格拉布斯准则、狄克逊准则和文献[9]粗大误差剔除方法来比较。其中N为各方法剔除粗大误差的循环迭代次数，W为传感器对应的权值。

表4 未剔除粗大误差

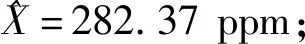
表5 格拉布斯准则处理结果

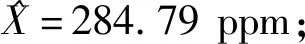
表6 狄克逊准则处理结果

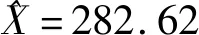
表7 文献[9]方法处理结果

表8 改进方法处理结果

从各方法的数据处理结果可以看出：格拉布斯准则可剔除单侧粗大误差，但对于同侧粗大误差会发生同侧异常值屏蔽效应。狄克逊准则可准确剔除粗大误差，但其迭代计算次数N等于粗大误差的数量，每次计算都需查表，算法效率低。文献[9]方法仅能剔除单侧粗大误差,且会错误剔除正常值。以数据处理后的标准差和计算迭代次数N为评价标准，可知改进数据预处理算法要优于狄克逊准则、文献[9]方法、格拉布斯准则。

对于无线传感器，需要综合考虑内存容量、计算量，数据处理的及时性，编程复杂度等方面。数据临界值表与计算迭代次数，会对无线传感器的内存、计算量提出较高的要求。改进算法可减少算法对内存空间和计算量的需求。

3 结束语

提出了一种改进的最优加权融合算法，主要对数据预处理阶段进行改进，使得各组自适应加权融合后的数据更接近真实值。从分析结果可以看出：

(1)粗大误差的剔除效率更高，仅需计算1次就可剔除多个粗大误差，减小处理器计算量。

(2)粗大误差的剔除更准确，可剔除单侧粗大误差、双侧粗大误差、同侧粗大误差。

(3)无需查询数据临界值表，节省处理器内存空间。