基于粗糙集与粒子群算法的权重优化模型研究







摘 要:针对服务质量评价中指标权重确定的问题,提出一种基于粗糙集与粒子群算法的权重优化模型。首先,利用粗糙集与模糊集,计算出初步权重并给出各个指标权重变化的区间,且在各区间内生成不同的权重值。再通过仿真实验来生成针对不同指标权重所产生的评价结果,定量计算出评价结果的方差。然后通过方差作为粒子群算法的适应度函数进行后向反馈,实现指标权重的优化。最后,将优化后的权重用于物流企业物流服务质量评价结果的计算。
关键词:物流服务;粗糙集理论;权重优化;粒子群算法
中图分类号:F224 文献标志码:A 文章编号:1673-291X(2022)13-0043-05
引言
多属性的评价过程中,需要对各个评价指标确定相应的属性权重。属性权重能够反映各属性因素在评价或决策过程中对评价结果所起的作用,并且指标权重的确定关系到评价方法的正确性和可靠性。因此,有关权重确定的方法研究一直是决策或评价领域研究的热点。国内外学者曾对指标权重优化展开研究。国内方面,张蕾(2017)构建了指标训练信息约简与粗糙集训练的改进方法,提升了模型权重优化的精度[1];江峰等(2018)提出基于粗糙熵的离群点优化模型,该模型具有较高的准确率和较低误报率,适用于海量高维数据运算[2];施振佺等(2019)提出基于知识粒度的属性加权算法,解决了依赖主观经验而权重优化不足的问题[3];崔利刚等人(2020)基于历史数据的模糊变量确定存在随机可能性判断的问题,证明粒子群算法对权重优化问题解决更有针对性[4]。国外方面,Jiang(2015)提出多变量监督式离散化粗糙集模型,解决了模型在算法优化时过早收敛的问题[5];He(2018)采用主成分分析法对指标进行聚类分析,并用粒子群算法对提取指标进行权重优化[6];Liu(2019)将结构风险最小化原理引入属性重要度的定义中,解决了传统粗糙集属性约简在高分类精度情况下不能保证优化质量的问题[7];Davoud(2021)提出了具有普适性的粒子群算法,通过加强多属性间内在关系,解决算法在优化时忽略属性间的交互作用而使得优化结果不理想的问题[8]。
综上所述,建立评价指标覆盖面全且各指标凝练的指标体系,可在一定程度上规避风险和事故。但在评价过程中,指标权重的确定依赖于专家的主观经验和知识等前向反馈机制调节,造成了评价结果说服力不够,同时无法依据标准的评价结果来重新调整设计指标权重,形成完善的反馈机制。
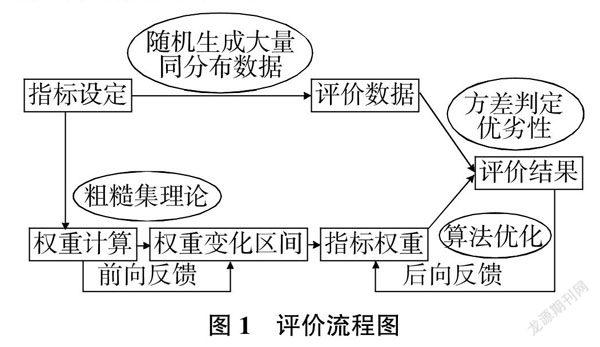
本文考虑将粗糙集理论和粒子群算法相结合,设计出一种新的指标权重优化的定量化方法来解决上述问题,议价流程见图1。
一、基于粗糙集理论确定指标初始权重
本文采用改进的粗糙集理论属性权重确定,考虑指标在指标集以及系统中的重要程度,引入条件熵的概念,确保每个条件属性的权重属性都不可能计算出为0的情况。改进后的权重系数计算方法如下。
(一)论域的分类
在决策表DT=(U,A,V,f)中,A=C∪D,C∩D=?覫,C={C1,C2,…,Cm}为条件属性集,D={D1,D2,…,Dk}为决策属性集。依次将论域U按照对某一条件属性ci、所有条件属性C、决策属性D以及去除某一条件属性ci后进行分类,得到U/ind(ci),U/ind(C),U/ind(D)和U/ind(C-ci)。
(二)条件熵的计算
在决策表DT=(U,A,V,f)中,A=C∪D,C∩D=?覫,C={C1,C2,…,Cm}为条件属性集,D={D1,D2,…,Dk}为决策属性集,则D相对于C的条件熵为:
(1)
(三)重要度的计算
在决策表DT=(U,A,V,f)中,?坌c∈C,a∈C,则条件属性c的重要度为:
(2)
式中,a(x)=U/{a}。
(四)权重系数的计算
在决策表DT=(U,A,V,f)中,?坌c∈C,则条件属性c的权重系数为:
(3)
二、基于粒子群算法优化指标权重
(一)权重变化区间的确定
可通过隶属度函数来初步确定权重值计算的变化区间,并以此来确定粒子群算法的搜索空间。选取高斯函数作为本文的隶属度函数如下所示:
(4)
式中,ci表示均值,?滓表示方差。
(二)指标打分数的生成
为了与实际情况尽可能地接近,数据都是基于式(5)所示的林德伯格—莱维的中心极限定理生成的,服从正態分布的相互独立随机数列,且与调研所获得的数据拥有相同的均值和方差。
(5)
(三)优化目标及算法的设定
1.优化目标。设计粒子群算法来求解下列数学问题:
(6)
(7)
(8)
(9)
上述模型中,Y表示生成的一组评价结果,Z表示各指标的随机打分数矩阵,X表示任意一组指标权重,Xi表示该组中第个指标的权重,x、x为权重波动的上下界。
2.粒子更新方式的设定。首先,根据式(10)确定需要改变的维度d′,然后根据粒子第d′维度的位置进行改变,此时权重为1的条件将被改变,这部分变化将由没发生位置更新的其他剩余维度共同承担,以确保粒子在位置更新之后的权重之和依然为1。
(10)
(11)
(12)
其中,v表示粒子i在k+1次迭代时第d个维度的速度,w表示惯性权重,c1、c2为两个正常数,称为加速因子,r1、r2为两个随机数,pid表示粒子i搜索到的最优位置,p表示所有粒子搜索到的最优位置,x表示粒子i在k次迭代时第d个维度的位置。
三、实例分析
(一)初始权重的生成
本文对国内相关物流企业的实际情况进行分析研究,依据物流服务质量中的关键要素,建立了包含20个评价内容的物流服务质量评价体系用于算例验证,具体见表1。
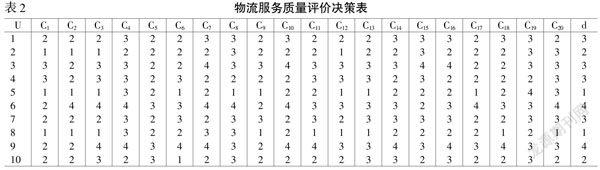
利用改进的粗糙集理论确定客观权重,以20个指标作为条件属性C,决策属性D={d},属性的值域V={1,2,3,4,5}。其中,“1”代表顾客对物流服务质量非常满意,“2”代表顾客对物流服务质量满意,“3”代表顾客对物流服务质量评价一般,“4”代表顾客对物流服务质量不满意,“5”代表顾客对物流服务质量非常不满意。在实地调研所收取的108份有效的调查问卷中,随机抽取10份作为计算原始数据,并且得到如下的物流服务质量评价决策见表2。
以条件属性c1为例进行权重计算,论域U对c1进行分类可得:
U/ind(c1)={{1,6,7,9,10},{2,5,8},{3.4}}
则论域U对所有条件属性C的分类为:
U/ind(C)={{1},{2},{3},{4},{5},{6},{7},{8},{9},{10}}
论域U对决策属性D的分类为:
U/ind(D)={{1,34,7},{2,10},{5,8},{6,9}}
在去除条件属性c1后,论域U对条件属性的分類为:
U/ind(C-c1)={{1},{2},{3},{4},{5},{6},{7},{8},{9},{10}}
由式(1)可得D相对于C的条件熵为:
I(D|C)=0
对条件属性c1,由式(1)得到D相对于c1的条件熵为:
去掉条件属性c1后,由式(1)得到D对{C-c1}的条件熵为:
根据式(2)得到条件属性c1的重要度为:
由式(3)可得到条件属性c1的权重系数为:
同理可以计算出c2至c20的初始权重系数分别为0.0505、0.0267、0.0364、0.0620、0.0390、0.0541、0.0709、0.0434、0.0576、0.0390、0.0364、0.0505、0.0505、0.0505、0.0470、0.0603、0.0532、0.0682、0.0603。
(二)权重变化区间的生成
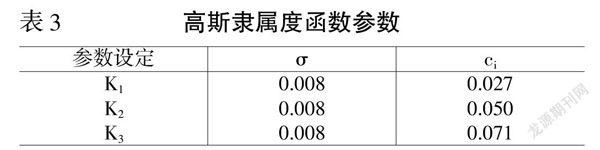
为了保证一般性,本文中3个隶属度函数均拥有相同的方差;在均值的选择上,3个高斯隶属度函数的均值分别设定为初始指标权重集合中最小值、平均值和最大值,以便能够通过隶属度函数的位置来均衡覆盖所有的权重指标,相关参数设定如表3所示。
将各指标权重的初始值带入上式(4)中计算隶属度,并根据最大隶属度原则,确定20个初始指标所处的等级,并且不能超出其现有等级。通过式(4)可以计算出图2中3条隶属度函数相交点的横坐标分别为0.0385和0.0605。
因此也可以得出各指标权重的变化区间见表4。
(三)粒子更新方式
根据上述设定的粒子群算法目标进行运算,得到粒子更新方式。本文将粒子在k次迭代时的其他19个维度的位置同时减少Δ/19。这种方法首先达到了粒子位置更新的目的,保证了粒子的多样性;其次,这种方法可以使得未发生更新的维度变化程度较小,不容易超出其所处的波动区间;再次,这种方式不会引起权重总和的变化。
(四)结果分析
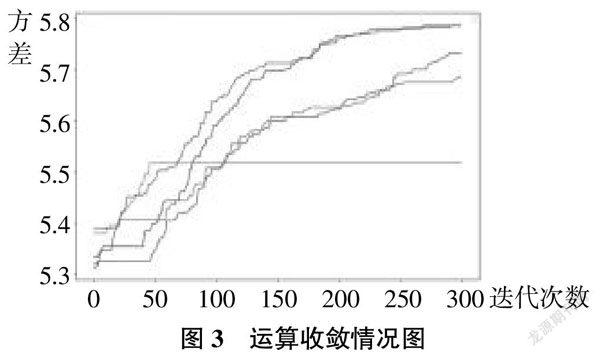
本文根据随机生成的打分数据和模糊理论等方法所得到的权重区间,以及所设计的粒子群算法,进行指标权重的优化,运算收敛情况见图3。
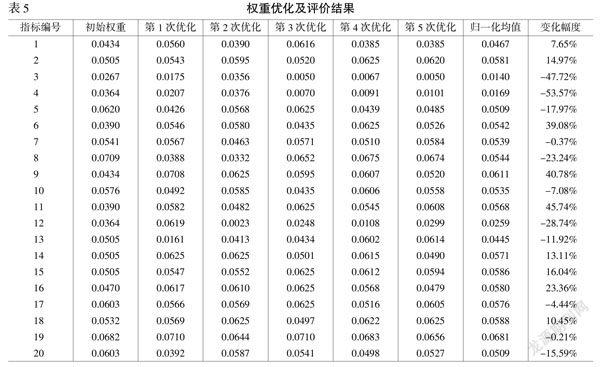
由图3可知,在基于不同随机打分数进行的多次算法优化中,除去一次优化运算在50次左右达到收敛,其余优化运算均在300次左右实现收敛。为了不失一般性,取5次优化中取得的最优平均值,并将其进行归一化处理,并以此作为最终的指标权重,用于实际项目中评价结果的计算见表5。
从表5可知,20个指标权重优化后的变化情况多样,变化幅度最小的是第7号指标,仅减少0.37%,说明该指标的初始权重基本可以代表其在全部指标中的重要程度;变化幅度最大的是第3号指标,指标权重经过算法优化后减小47.72%,说明对于该指标的初始权重设定过大,为获得合理的评价结果,应减少该指标权重值。
为验证该优化方法的合理性,本文根据表5中优化的权重指标和初始权重指标,对我国10个物流服务企业进行服务质量评价,评价结果对比见表6。
表6中,评价结果1表示基于初始权重计算出的物流服务质量评价结果,评价结果2表示经过优化后的权重计算出的物流服务质量评价结果。由最后的方差数据可知,经过权重优化后,对10个物流企业的物流服务质量评价结果的方差由先前的104.3提升为125.4,方差扩大20.2%。结果分布更加趋于分散,有效区分了不同物流企业的物流服务质量状况,从而为相关物流企业的管理和服务质量的提升提供更加准确客观的数据参考。
结语
本文基于粗糙集理论和粒子群算法建立的反馈调节模式,提出了一种在质量评价中指标权重确定的定量化方法,在一定程度上弥补了指标权重在确定过程中主观性较强的问题。基于本文得出的结果,对全文进行如下总结:粗糙集理论能够弱化专家打分的主观性,具有一定可行性。研究表明,以专家打分数为基础生成的模糊区间,可以在充分尊重原始数据的基础上,降低评价过程中的主观性,提高评价结果的可行性。同时以评价结果的方差作为评价结果优劣的评估标准,具有一定合理性。而对多次随机打分数生成的多次评价结果的方差,可以在评价范围的覆盖率和评价结果变化的敏感性两个方面评判评价结果的优劣性,从而构建评价指标权重的负反馈机制。
参考文献:
[1] 张蕾.基于粗糙集和Markov链的供应链管理绩效评价[J].统计与决策,2017,(24):15.
[2] 江峰,王凯郦,于旭,眭跃飞,杜军威.基于粗糙熵的离群点检测方法及其在无监督入侵检测中的应用[J].控制与决策,2020,(5):1199-1204.
[3] 施振佺,陈世平.一种改进的k-modes聚类算法[J].运筹与管理,2019,(12):112-117.
[4] 崔利刚,任海利,邓洁,张亚军.基于模糊随机需求的B2C多品采配协同模型及其粒子群算法求解[J].管理工程学报,2020,(11):1-8.
[5] Jiang F.,Sui Y.A novel approach for discretization of continuous attributes in rough set theory[J].Knowledge-Based Systems,2015,(73):324-334.
[6] He Y.,Pang Y.,Zhang Q.,et al..Comprehensive evaluation of regional clean energy development levels based on principal component analysis and rough set theory[J].Renewable Energy,2018,(122):643-653.
[7] Liu J.,Bai M.,Jiang N.,et al..A novel measure of attribute significance with complexity weight[J].Applied Soft Computing,2019,(82):105543.
[8] Sedighizadeh D.,Masehian E.,Sedighizadeh M.,et al.GEPSO:A new generalized particle swarm optimization algorithm[J].Mathematics and Computers in Simulation,2021,179:194-212.
Research on Weight Optimization Model based on Rough Set and Particle Swarm Optimization
SHAO Jun-jie
(School of Business Jiangnan University,Wuxi 214122,China)
Abstract:In terms of the problem of index weight determination in service quality evaluation,the paper proposed a weight optimization model based on rough set theory and particle swarm optimization.Firstly,it combines the rough set theory and the fuzzy set theory to calculate the initial weight and give the interval of each index weight change,and generate different weight values in each interval.And through simulation experiments to generate evaluation results for different index weights,and quantitatively calculate the variance of the evaluation results.Then the variance is used as the fitness function of the particle swarm algorithm to perform backward feedback to optimize the index weights.Finally,the optimized weights are used in the calculation of the evaluation results of the logistics service quality of the logistics enterprises.
Key words:logistics service;rough set theory;weight optimization;particle swarm optimization
收稿日期:2021-03-29
作者簡介:邵俊杰(1996-),男,江苏常熟人,硕士研究生,从事不确定性决策与预测、供应链管理研究。

