高超声速滑翔飞行器协同轨迹规划方法

王新宇 梁学智 施锐 张栋

摘 要：  为了满足高超声速滑翔飞行器协同再入的时间和角度需求，考虑过程约束和交班点约束，提出了一种多约束协同再入轨迹规划算法。将时间约束和角度约束分解到纵向和横向两个平面，采用牛顿迭代法规划阻力加速度-能量剖面，得到满足时间和航程约束的纵向轨迹，利用序列二次规划方法搜索倾侧角翻转点，使轨迹终端满足角度约束，通过多次迭代更新，可以得到满足时间和角度约束的三维轨迹。在此基础上，分析了单个飞行器的飞行能力，给出了协同参数的确定方法。数值仿真结果表明，该方法能够在协同打击、协同投递等多种场景中应用，为飞行器规划出具有较高时间和角度精度的三维轨迹，任务适应性强，能够满足更多的约束和协同需求。

关键词：高超声速飞行器；协同再入；轨迹规划；时间协同；方向协同；协同策略

中图分类号：TJ765；V412.4

文献标识码：A

文章编号：1673-5048（2022）05-0001-10

DOI：10.12132/ISSN.1673-5048.2022.0097

0 引  言

高超声速滑翔飞行器是一种由火箭助推至高空或者从卫星发射的高超声速飞行器，该类飞行器通常具有大升阻比的气动特性，飞行马赫数超过5，能够在大气层内进行远距离滑翔［1］。凭借飞行高度高、速度大、射程远、机动能力强等出众的性能特点［2-3］，高超声速滑翔飞行器在远程突防和精确打击等领域有着广泛应用［4］。

近年来，由于防空反导技术快速发展，单枚飞行器的突防能力持续被削弱，为了继续保持高超声速再入滑翔飞行器的作战优势，一些学者提出将集群控制技术应用在高超声速滑翔飞行器上，通过多枚高超声速滑翔飞行器协同飞行，相互配合，共同执行任务，从而扩展高超声速滑翔飞行器的应用领域，增加高超声速滑翔飞行器的突防概率。

集群控制技术中应用较多的是以无人机、巡航导弹为对象的编队控制技术，通过领-从式策略、虚拟刚体策略等控制多枚飞行器协同飞行。但是无人机和巡航导弹的很多协同制导方法都应用了定常匀速假设，且飞行过程中的约束比较少。与其相比，高超声速滑翔飞行器的再入过程是无动力滑翔，速度无法直接控制，而且飞行环境复杂，需要考虑热流密度、动压等过程约束，另外飞行速度较快、分布空域大，弹间通信不便，所以相关编队控制技术无法直接应用在高超声速滑翔飞行器上。为了解决高超声速滑翔飞行器的协同问题，一些学者改变思路，通过协同轨迹规划，根据一定协同策略为每枚高超声速滑翔飞行器规划相应的轨迹，从而可以在轨迹的终端实现某一方面的协同。

对于时间协同的研究中，文献［5］通过对到达时间进行预测，得到协同飞行时间，以此作为终端时间约束，基于Radau伪谱法进行轨迹优化，从而实现时间协同。文献［6］将飞行时间误差加入到罚函数中，提出了一种基于序列凸优化的协同轨迹快速规划算法，提高了协同轨迹求解的可行性与计算速度。文献［7］建立剩余飞行时间和末制导交班点速度的对应关系，运用预测-校正方法，同时满足末端能量和时间约束。文献［8］设计了一种动态参考剖面，通过对攻角剖面和高度-速度剖面的参数进行不断校正，使飞行器轨迹满足时间约束。文献［9］基于双参数牛顿迭代法设计阻力加速度剖面，结合可调边界的航向偏差走廊，生成满足时间约束的参考轨迹。文献［10］基于非线性再入动力学方程推导出高精度的飞行时间解析解，设计了满足时间约束的飞行轨迹。

此外，文献［11］基于神经网络建立航向偏差走廊和飞行时间的关系，使轨迹满足时间约束。文献［12］采用深度Q-学习网络求解飞行器横向机动解析解，实现时间协同再入飞行。文献［13］利用多边界航向偏差走廊调节飞行时间，使多枚飞行器同时到达目标。文献［14］运用模型预测静态规划（MPSP），求解具有硬终端约束的飞行器协同再入控制指令，实现对多个目标的协同打击。与时间协同相比，方向协同的研究文献较少，文献［15］通过序列二次规划方法（SQP）搜索满足接近角约束的地面瞄准点，实现航天器固定角度再入。文献［16］研究了助推滑翔飞行器的弹道特点，采用设置虚拟目标点的方式控制飞行器到达目标的角度。

以上学者大多数只研究了时间协同和方向协同的一种，并未将两种协同方式结合，无法满足饱和打击、协同运输等任务需求。针对该问题，本文在文献［9］和［15］的基础上进行改进，提出一种能够同时满足时间约束和角度约束的协同轨迹规划方法。首先，设计攻角剖面，采用牛顿迭代法设计阻力加速度-能量剖面，得到满足时间、航程等约束的纵向轨迹。然后，采用SQP方法搜索满足角度约束的倾侧角的翻转能量点，从而通过轨迹规划实现单枚飞行器的时间、角度控制。在此基礎上，分析单枚飞行器的飞行能力，提出协同时间和协同方向的确定方法，实现多枚飞行器的时间、方向协同轨迹规划。最后，通过仿真证明了本文提出的协同轨迹规划方法的有效性。

1 多飞行器协同再入问题描述

1.1 协同再入问题

1.1.1 协同需求

在高超声速滑翔飞行器协同打击、协同投递等典型作战场景中，根据作战任务，多枚飞行器再入飞行存在相应的协同需求。图1为多枚高超声速滑翔飞行器对目标协同打击的场景示意图，图2为多枚高超声速滑翔飞行器协同投递小型飞行器作战的场景示意图。

图1中，多枚高超声速滑翔飞行器从发射阵地发射后，向目标阵地协同飞行，期望同一时刻从不同方向对目标进行协同打击，从而增加突防概率，提高对目标的杀伤效果。图2中，多枚高超声速滑翔飞行器从发射阵地发射后，向目标阵地协同飞行，在不同时间以相同方向到达固定区域进行协同投递，抛撒小型飞行器，使小型飞行器快速集结成编队，对目标进行蜂群作战。

从两个典型场景中可以看出，协同再入飞行常见的协同需求有时间协同和方向协同，时间协同又有同时刻协同和分批次协同两种，方向协同又有相同方向和不同方向两种，而且常常两种协同需求需要同时得到满足。

1.1.2 协同阶段

根据高超声速滑翔飞行器的受力以及飞行环境变化，可以将飞行过程分为主动段、自由飞行段、再入滑翔段和下压段。图3为高超声速滑翔飞行器的弹道示意图，展示其主要飞行阶段。

在高超声速滑翔飞行器的主要飞行阶段中，主动段和自由飞行段作为初始阶段，飞行时间短、机动能力弱，弹道相对固定，难以进行协同规划；下压段作为最后飞向目标的阶段，飞行距离和时间比较短，同样不适合进行协同飞行；而再入滑翔段占据了整个飞行过程80%以上的航程，飞行时间长、机动能力较强，所以适合作为协同飞行的主要阶段。

1.2 飞行器数学模型

1.2.1 动力学模型

高超声速滑翔飞行器的再入飞行环境和动力学模型较为复杂，建模时考虑所有的因素不利于分析其飞行特性。为了简化问题，将影响较小的因素忽略，对飞行器运动过程进行简化，作如下假设：

（1） 将地球看作一个均质球体；

（2） 将飞行器看作是一个质点；

（3） 再入过程中飞行器质量不变；

（4） 忽略外界的干扰。

高超声速滑翔飞行器采用BTT方式转弯，所以侧滑角β=0°，而且再入段无推力作用，在大地坐标系下建立第i枚高超声速滑翔飞行器的三自由度动力学方程：

dridt=Visinθi

dVidt=－Ximi－gsinθi

dθidt=1ViYicosσimi+V2iri－gcosθi

dψidt=1ViYisinσimicosθi+V2iricosθisinψitani

dλidt=－Vicosθisinψiricosi

didt=Vicosθicosψiri （1）

式中：下标i代表第i枚飞行器；λ为飞行器经度；为飞行器纬度；r为飞行器与地心距离；V为飞行器速度；θ为弹道倾角；ψ为航向角；σ为倾侧角；m为飞行器质量；g为重力加速度， g=g0R20r2；

X和Y分别为飞行器所受的阻力和升力：

X=Cx（Ma， α）qSrefY=Cy（Ma， α）qSref

式中：α为气动攻角；Ma为马赫数，是飞行器速度与当地声速的比值；Sref为参考面积；Cx，Cy分别为阻力系数和升力系数，可以通过攻角与马赫数对气动系数插值表二维插值得到；q为动压。

q=12ρV2

式中：ρ=ρ0exp－HHs为大气密度，

Hs=6 700 m， ρ0=1.752 kg/m3， H=r－R0， R0为地球半径。

1.2.2 约束模型

高超声速滑翔飞行器再入飞行过程中，考虑到外界环境、飞行器材质以及飞行任务的影响，飞行器需要满足以下约束。

（1） 过程约束

第i枚飞行器的热流密度、动压、过载需要满足以下约束：

qi=12ρiV2i≤qmax

Q·I=kQ·ρ0.5iV3.15i≤Q·maxni=X2i+Y2i/（mig）≤nmax （2）

攻角αi（t）和倾侧角σi（t）需要满足：

|αi|≤αmax|σi|≤σmax （3）

（2） 终端约束

对于多枚飞行器协同再入，滑翔段终端条件不仅需要满足速度、高度和待飞航程约束，对于有时间和方向协同要求的飞行器，还需要考虑时间、航向角和视线角的约束：

Vi（ti， f）=V*i

Hi（ti， f）=H*i

si（ti， f）=s*i

ti， f=t*i

ψi（ti， f）=ψ*i

φi（ti， f）=φ*i （4）

式中：航向角ψ定义为飞行器速度方向与正北方向的夹角，以北转东为正；视线角φ定义为飞行器与目标的连线与正北方向的夹角，以北转东为正。

2 带时间和角度约束的三维轨迹规划

将三维轨迹规划过程分为纵向轨迹设计和横向制导逻辑设计两部分。如图4所示，首先，设计攻角剖面求解使纵向轨迹满足时间约束和航程约束的阻力加速度剖面；然后，搜索倾侧角翻转能量点，使三维轨迹满足角度约束；最后，由于飞行器的横向运动会导致终端待飞航程出现误差，因此需要更新阻力加速度剖面，然后再次搜索倾侧角翻转点，经过多次迭代，可以逐步减小误差，得到满足时间、角度约束的三维轨迹。

2.1 基于阻力加速度剖面的纵向轨迹规划

纵向轨迹规划过程主要是设计攻角剖面和阻力加速度剖面，通过跟踪参考剖面得到满足时间、航程等约束的纵向轨迹。

2.1.1 攻角剖面

将飞行器攻角剖面设计为分段形式，参考攻角αc随速度v变化的表达式为

αc=α1         V0≥V>V1α1+α2－α1V2－V1（V－V1）  V1≥V>V2

α2+α3－α2Vf－V2（V－V2）  V2≥V>Vf （5）

式中：V1，V2为中间速度值；α1为大攻角；α2为中间攻角； α3为最大升阻比对应攻角。

2.1.2 阻力加速度剖面

以归一化能量为自变量，将阻力加速度剖面设计为三段折线的形式。阻力加速度-归一化能量剖面示意如图5所示。

图中再入走廊上边界由熱流密度、过载、动压约束确定，下边界由平衡滑翔条件确定，计算公式为

DQ·≤CxSQ·2max2mV4.3C2Q·

Dn≤nmaxg1+CyCx2

Dq≤CxqmaxSm

Dglide=g－V2rCyCxcosσ （6）

再入走廊内阻力加速度曲线的表达式为

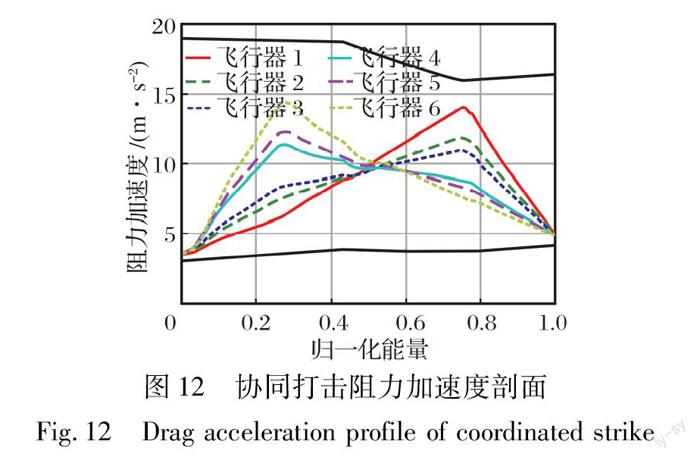
D（e）=D0+D1－D0e1－e0（e－e0）e0≤e

D1+D2－D1e2－e1（e－e1）e1≤e

D2+Df－D2ef－e2（e－e2）e2≤e

由于初始节点和终端节点确定，可依据乔浩等［9］提出的方法，给定e1，e2，采用二元牛顿迭代法求解D1，D2，从而确定阻力加速度剖面。

设e1，e2对应的再入走廊上、下边界值分别为Dup（e1），Ddown（e1），Dup（e2），Ddown（e2），由于要满足过程约束，所以要求D1，D2满足下列约束：

Ddown（e1）≤D1≤Dup（e1）

Ddown（e2）≤D2≤Dup（e2） （8）

考虑时间t和航程S约束，建立二元方程组：

F（D1， D2）=tf－t*=0

G（D1， D2）=Sf－S*=0 （9）

初始航程约束设为起点与目标点的星下点轨迹距离。根据仿真经验，设置阻力加速度节点初值，采用牛顿迭代法求解该方程组，牛顿迭代公式为

D1， i+1=D1， i+FGD2－GFD2GD1FD2－FD1GD2D2， i+1=D2， i+GFD1－FGD1GD1FD2－FD1GD2 （10）

当参考剖面确定，跟踪参考阻力加速度曲线，可以得到满足时间、航程约束的纵向轨迹。

当飞行器横向运动，导致航程约束对应轨迹不满足待飞航程约束，需要对航程约束值进行更新，重新规划阻力加速度剖面，更新公式如下：

Sk+1=Sk+Δs（11）

式中：Δs为上一次规划轨迹的待飞航程偏差。

以倾侧角的余弦值作为控制变量，建立二阶线性误差动力学方程：

（D″－D″c）+2ξω（D′－D′c）+ω2（D－Dc）=0（12）

设阻力加速度对归一化能量的二阶导数为

d2Dde2=a+bCyCxcosσ（13）

式中：a，b为系数。求解控制变量与倾侧角幅值：

u=1bCxCy（D″c－2ξω（D′－D′c）－ω2（D－Dc）－a）（14）

σ=arccosu（15）

2.2 基于倾侧角翻转能量点的横向机动策略

当飞行器的纵向轨迹确定后，通过设计能量点，使飞行器在满足翻转能量条件时改变倾侧角符号，使三维轨迹终端满足角度约束。

2.2.1 终端倾侧角符号

根据初始视线角φ1和要求视线角φ*的大小，设计相应的终端倾侧角。

由于飞行器向目标飞行时，通常是沿着视线飞行，所以假设飞行器在接近目标时航向角与视线角一致，且等于初始视线角。图6中，起始点1的初始视线角φ1>φ*，飞行器在接近目标点时，航向角ψ1>ψ*，若终端倾侧角符号为正，飞行器会进行右机动，航向角会不断增加，与终端航向角约束值的偏差增加；若终端倾侧角符号为负，飞行器进行左机动，航向角减小，才可能满足终端航向角约束。起始点2的情况与起始点1相反，起始点2的初始视线角φ2<φ*，航向角ψ2<ψ*，若终端倾侧角符号为负，飞行器左机动，航向角减小，终端航向角偏差增加；若终端倾侧角符号为正，飞行器右机动，航向角增大，才可能满足角度约束。

综上，根据飞行器初始视线角φ0与要求角度φ*的大小，设计终端倾侧角符号：

sgn（σf）=1φ0<φ*－1φ0≥φ* （16）

2.2.2 倾侧角翻转次数

当终端倾侧角符号确定后，可以根据飞行器初始倾侧角符号设计飞行器在飞行过程中倾侧角的翻转次数，下面以图7中飞行器的两种翻转情况为例进行分析。

在图7中，Case 1中飞行器的初始倾侧角符号与终端一致，至少要翻转两次才能保证满足终端倾侧角符号要求。Case 2中初始倾侧角符号与终端倾侧角符号相反，至少要翻转一次才能保证满足终端倾侧角符号要求，但是考虑到飞行轨迹需要满足较多约束，一次翻转机动能力有限，所以最好翻转三次以满足规划要求。

综上，根据飞行器初始倾侧角符号sgn（σ0）与终端倾侧角符号sgn（σf），翻转次数设为

n=2  sgn（σ0）=sgn（σf）

3  sgn（σ0）=－sgn（σf） （17）

2.2.3 倾侧角翻转能量点

若飞行器有n个倾侧角翻转能量点ei，当飞行器的能量e∈（ei， ei+1），飞行器的倾侧角符号为

sgn（σ）=（－1）isgn（σ0） i=0， 1， 2， …， n（18）

为了使飞行器轨迹终端满足角度约束，采用SQP方法搜索倾侧角翻转能量点。

设计目标函数为

J=ω·φ（ef）－φ*Δφmax2+（1－ω）·ψ（ef）－ψ*Δψmax2（19）

式中：Δφmax和Δψmax分别为允许的视线角和航向角的最大误差；ω为权重系数，ω∈0，  1。轨迹积分以e=ef为停止条件。

3 协同规划策略

3.1 飞行能力分析

3.1.1 D1，D2对时间和航程的影响

以CAV-L飞行器为例，仿真分析固定航程下，D1，D2对飞行时间的影响，以及固定时间下，D1，D2对总航程的影响，仿真结果如图8～9所示。

由图8可以看出，固定航程约束下，D1增加，D2減小时，飞行器到达时间增加；而D1减小，D2增加时，飞行器到达时间减小。由图9可以看出，固定时间约束下，D1增加，D2减小时，飞行器的航程减小；而D1减小，D2增加时，飞行器的航程增加。

3.1.2 单枚飞行器的时间调节范围

在计算单枚飞行器的时间调节范围时，选择通过大圆弧假设求得的再入点到目标的距离作为总航程约束，通过设计不同的D1，D2获取飞行器的最大、最小到达时间。根据图9得到的结论，若计算最大到达时间，可以给定一个较大的D1，通过牛顿迭代法求解满足航程约束的D2；若计算最小到达时间，可以给定一个较小的D1，通过牛顿迭代法求解满足航程约束的D2，从而得到飞行器到达时间的调节范围。

3.2 协同参数确定方法

在进行协同轨迹规划之前，需要获取到所有飞行器的飞行能力和作战任务，然后对信息进行处理，根据一定的策略确定协同时间和协同方向。

3.2.1 协同方向

飞行器集群的协同方向通常由作战任务确定，如对于多飞行器协同投递任务，需要将大量无人机抛撒在一个较小的区域，而且飞行方向尽量一致，所以让飞行器集群以相同的方向到达投递区域，协同方向可以设置为再入点到抛撒点的视线方向；而对于多飞行器协同打击任务，为了增加突防概率，躲避敌方探测雷达和防空导弹，使多个飞行器从多个方向进入目标区域，协同方向可以设置为敌方防御薄弱的多个方向。

3.2.2 协同时间

考虑多飞行器同时到达目标区域和分批次到达目标区域两种情况，计算协同到达时间。

（1） 多飞行器同时到达同一目标

Step 1：求解各飞行器从起点到目标点的最长飞行时间tmax， i和最短飞行时间tmin， i；

Step 2：计算多飞行器协同到达时间可选范围：

tmin=max{tmin， 1， …， tmin， i， …， tmin， n}

tmax=min{tmax， 1， …， tmax， i， …， tmax， n} （20）

Step 3：考虑到再入过程中的扰動，为了增加飞行器对到达时间的适应性，需要留一定余量，计算协同时间：

t=tmin+tmax2（21）

（2） 多飞行器分批次到达同一目标

Step 1：求解各飞行器从起点到目标点的最长飞行时间和最短飞行时间tmax， i，tmin， i，i=1， 2， …， n；

Step 2：计算多飞行器协同到达时间可选范围：

tmin=max{tmin， 1， …， tmin， i， …， tmin， n}

tmax=min{tmax， 1， …， tmax， i， …， tmax， n} （22）

Step 3：若存在m批飞行器，第k与第k+1批次到达时间间隔为Δtk， k+1，其中k=1， 2， …， m－1，则第j批飞行器到达时间设置为

tj=tmin+tmax－tmin－∑m－1k=1Δtk， k+12+∑j－1k=1Δtk， k+1（23）

Step 4：为每个飞行器划分批次，确定到达时间ti。

4 数值仿真

以CAV-L为对象，通过Matlab平台对算法进行仿真验证。再入飞行过程中，考虑过载约束nmax=4g，热流密度约束Q·max=1 200 kW/m2，动压约束qmax=2×103 kPa，最大攻角约束为20°，最大倾侧角约束为80°。仿真时间间隔为0.1 s，牛顿迭代法的航程允许误差为1 km，时间允许误差为0.2 s，而且采用SQP方法的轨迹终端角度允许误差为1°。设置可接受的终端时间、航向角、待飞航程、高度、速度偏差为2 s，5°，3 km，0.5 km，5 m/s。

4.1 多飞行器协同打击仿真

假设有6枚CAV-L飞行器从不同阵地发射，要求对目标进行协同打击，考虑到敌方防空力量，采用多方向突防的方式，要求6枚飞行器同时刻以不同方向到达目标区域。飞行器的初始参数如表1所示，终端约束如表2所示，飞行器终端状态如表3所示。

（1） 仿真图表分析

从图10～11可以看出，6枚飞行器从不同位置出发，经过一定的机动，最终从不同方向到达目标区域，实现了协同打击任务。从图12可以看出，6枚飞行器的阻力加速度曲线都在再入走廊内，满足热流密度、动压等过程约束，而且初始阻力加速度和终端阻力加速度节点一致，由于航程不同，为了能够满足时间约束，不同飞行器的阻力加速度曲线也有所偏差。从图13可以看到，6枚飞行器的初始高度、速度一致，在飞行过程中，高度随速度的变化规律发生变化，但是在接近终端的过程中，飞行器的速度和高度逐渐收敛到约束值。从图14可以看到，飞行器的参考攻角最初保持最大值，当速度下降到一定值后，参考攻角的值不断减小，最终减小到最大升阻比对应攻角上不变，与设计方法一致。从图15可以看出，由于6枚飞行器的初始视线角都小于约束角度值，而1、2、3、4号飞行器的初始倾侧角符号为正，5、6号飞行器初始倾侧角符号为负，所以飞行过程中1、2、3、4号飞行器的倾侧角翻转了两次，5、 6号飞行器翻转了3次，与倾侧角翻转策略一致，同时在图中，倾侧角曲线几乎都存在5次较大的抖动，这是因为参考攻角剖面和参考阻力加速度剖面都各自存在2个中间节点，在节点处的攻角曲线和阻力加速度曲线连续但是不可导，所以采用制导律跟踪参考剖面时无法平滑地跟踪参考曲线，总会出现一定的偏差，而且实际阻力加速度曲线导数与飞行器的弹道倾角相关，在初始时刻，弹道倾角是给定值，与规划的参考阻力加速度曲线不符，所以在跟踪阻力加速度剖面时会出现跟踪偏差，体现在倾侧角剖面上就是较大的抖动。根据协同策略计算协同到达时间t*=420 s，从表3可以看到，6枚飞行器的轨迹终端参数与约束值的误差较小，待飞航程和高度误差均在1 km以内，速度偏差均在1m/s以内，而且6枚飞行器的到达时间一致，最终的时间误差近乎为0，终端的航向角与视线角误差均在1°以内，6枚飞行器在满足多种约束的情况下同时刻从不同的方向到达目标区域，可以执行协同打击任务，由此也验证了协同轨迹规划算法的有效性。

（2） 轨迹规划分析

由于飞行器的横向运动会增加横向航程，所以在设计倾侧角翻转能量点后， 飞行器在要求时间无法到达目标，需要对阻力加速度剖面和倾侧角翻转点进行更新，每一次更新都可以认为一次迭代，以1号飞行器为例，分析其轨迹规划算法的计算速度与收敛性。表4为轨迹规划的纵向轨迹设计与横向翻转点设计迭代计算过程的部分参数。

从表4数据可以看出，以归一化能量e=1为轨迹终端，此时飞行器的飞行时间满足约束条件，但是由于第一次迭代初始航程约束是起点-终点的星下点轨迹，进行横向运动后初始航程约束不能使飞行器满足终端待飞航程约束，待飞航程明显偏大，所以将待飞航程的偏差值补偿到航程约束，更新航程约束值。以上一次规划的阻力加速度节点和倾侧角翻转能量点为初值，进行第二次迭代，再次规划阻力加速度剖面和倾侧角翻转能量点。第二次的规划结果中待飞航程误差明显减小，符合误差要求，第三次迭代与第二次结果相近，停止迭代。

第一次迭代计算时，阻力加速度节点和倾侧角翻转能量点给定的初值与实际值相差比较大，迭代搜索耗费的时间较长。在第二次、第三次迭代时，以上一次的迭代结果作为初值，所以迭代搜索时间减小，终端误差也快速下降，实现收敛。

4.2 多飞行器协同投递仿真

假设有6枚CAV-L飞行器携带大量不同功能的小型蜂群飞行器协同飞行，根据功能与任务，将其等分成3个批次，每批次两个飞行器，以相同的方向依次到达要求区域，然后进行协同投递，从而执行“侦察-打击-评估”一体化任务。飞行器的初始参数如表5所示，终端约束如表6所示。

从表5可以看出，6枚高超声速滑翔飞行器的位置较为集中，且初始高度、速度一致；从表6可以看出，瞄准位置有两个，因此同一批次的两枚飞行器分别向不同的瞄准点飞行，避免发生碰撞。根据协同策略，确定协同到达时间和协同方向。

从表7可以看到，6枚飛行器的到达时间偏差近乎为0，航向角和视线角偏差小于1°，待飞航程偏差在1 km以内，高度偏差在1 km以内，速度偏差小于1 m/s，各飞行器的终端状态与约束值相比均保持较高的精度，说明该方法可以实现多飞行器分批次以相同方向的协同投递任务，再次证明了本文提出协同轨迹规划方法的有效性与在多种任务场景中应用的普适性。

从图16～17可以看出，6枚飞行器以相同方向到达抛撒点，而且飞行时间长的飞行器侧向机动幅度明显更大。从图18可以看出，6枚飞行器的阻力加速度曲线都在再入走廊内，满足过程约束，而且飞行时间比较长的飞行器前期阻力加速度较大，后期减小，飞行时间短的飞行器前期阻力加速度较小， 后期增加。 从图19可以看到，6枚飞行器的高度随速度下降速率不同。其中，飞行器5、6号的高度在前期快速减小，明显小于其他飞行器，在后期又减缓下降速度，高于其他飞行器，最后趋于一致。这是因为飞行器5、6号的时间约束大，为了增加飞行时间，需要在前期快速下降，周围的空气密度增加，从而使阻力大幅度增加，速度下降，在之后的航程中飞行更长的时间。而飞行器1、2号的时间约束小，为了快速到达要求位置，需要保持高速，所以前期高度较高，空

气密度小，阻力小，速度快；在后期飞行中，为了满足高度、速度约束，增加阻力加速度，使高度、速度快速下降。从图20可以看到，飞行器的攻角在约束范围内，且变化规律与设计函数一致。从图21可以看出，6枚飞行器均翻转了两次，且倾侧角在约束范围内。

5 结  论

本文提出一种高超声速滑翔飞行器再入协同轨迹规划算法，能够根据各飞行器的飞行能力与作战任务，计算协同时间和协同方向，并且规划出满足时间约束和角度约束的三维轨迹。结论如下：

（1） 将阻力加速度剖面设计为折线形式，调节阻力加速度曲线的节点可以生成不同飞行时间和航程的纵向轨迹，以时间和航程偏差建立二元方程组，通过牛顿迭代法可以求解出满足时间约束和航程约束的纵向轨迹。

（2） 提出倾侧角翻转策略，根据飞行器初始位置、目标位置以及初始倾侧角符号，确定飞行器再入轨迹的终端倾侧角符号和倾侧角翻转次数，以终端角度为优化目标，采用SQP方法得到满足终端角度约束的倾侧角符号。

（3） 将时间约束和角度约束分解到纵向与横向轨迹设计，通过设计阻力加速度剖面与倾侧角翻转能量点实现相应约束，通过迭代消除横向与纵向规划之间的干扰误差，可以得到满足时间和角度等多种约束的三维轨迹。

（4） 分析飞行器的飞行能力与时间调节范围，根据多枚飞行器的能力与作战任务进行协同规划，确定协同时间和协同方向，将三维轨迹规划与协同规划策略相结合，以满足多种作战任务的协同需求。

（5） 协同打击和协同投递的数值仿真表明，该方法可以在多种作战场景中应用，能实现多种任务模式不同协同要求的轨迹规划，而且规划的轨迹具有较高的精度。

参考文献：

［1］ Zhao J， Zhou R， Jin X L. Progress in Reentry Trajectory Planning for Hypersonic Vehicle［J］. Journal of Systems Engineering and Electronics， 2014， 25（4）： 627-639.

［2］ 王少平， 董受全， 隋先辉， 等. 助推滑翔高超声速导弹发展趋势及作战使用研究［J］. 战术导弹技术， 2020（1）： 9-14.

Wang Shaoping， Dong Shouquan， Sui Xianhui， et al. Research on Development and Operational Application of Boost-Glide Hypersonic Missile［J］. Tactical Missile Technology， 2020（1）： 9-14.（in Chinese）

［3］ Liang Z X， Ren Z， Li Q D， et al. Decoupled Three-Dimensional Entry Trajectory Planning Based on Maneuver Coefficient［J］. Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering， 2017， 231（7）： 1281-1292.

［4］ 陈法龙. 高超声速滑翔飞行器弹道快速规划研究［D］. 长沙： 国防科学技术大学， 2012.

Chen Falong. Research of Rapid Trajectory Planning for Hypersonic Glide Vehicle［D］. Changsha： National University of Defense Technology， 2012. （in Chinese）

［5］ 李征， 彭博， 陈海东， 等. 可重复使用航天器时间协同飞行轨迹优化［J］. 计算机仿真， 2020， 37（1）： 40-45.

Li Zheng， Peng Bo， Chen Haidong， et al. Time-Coordination Reentry Trajectory Design for Reusable Launch Vehicle［J］. Computer Simulation， 2020， 37（1）： 40-45.（in Chinese）

［6］ 刘哲， 陆浩然， 郑伟， 等. 多滑翔飞行器时间协同轨迹快速规划［J］. 航空学报， 2021， 42（11）： 524497.

Liu Zhe， Lu Haoran， Zheng Wei， et al. Rapid Time-Coordination Trajectory Planning Method for Multi-Glide Vehicles［J］. Acta Aeronautica et Astronautica Sinica， 2021， 42（11）： 524497.（in Chinese）

［7］ 韩嘉俊， 王小虎， 郝昀， 等. 带有时间约束的再入滑翔轨迹设计［J］. 宇航学报， 2020， 41（4）： 438-446.

Han Jiajun， Wang Xiaohu， Hao Yun， et al. Reentry Trajectory Planning with Flight Time Constraints［J］. Journal of Astronautics， 2020， 41（4）： 438-446.（in Chinese）

［8］ 王浩凝， 唐勝景， 郭杰， 等. 带有动态攻角剖面的时间约束再入制导［J］. 空天防御， 2021， 4（1）： 71-76.

Wang Haoning， Tang Shengjing， Guo Jie， et al. Time-Constrained Reentry Guidance with Dynamic Angle of Attack Profile［J］. Air ＆ Space Defense， 2021， 4（1）： 71-76.（in Chinese）

［9］ 乔浩， 毛瑞， 白凤科， 等. 带时间约束的双参数再入轨迹设计方法［J］. 弹箭与制导学报， 2021， 41（3）： 57-61.

Qiao Hao， Mao Rui， Bai Fengke， et al. A Two-Parameter Reentry Trajectory Design Method with Time Constraints［J］. Journal of Projectiles， Rockets， Missiles and Guidance， 2021， 41（3）： 57-61.（in Chinese）

［10］ Yu W B， Chen W C， Jiang Z G， et al. Analytical Entry Guidance for Coordinated Flight with Multiple No-Fly-Zone Constraints［J］. Aerospace Science and Technology， 2019， 84： 273-290.

［11］ 方科， 张庆振， 倪昆， 等. 高超声速飞行器时间协同再入制导［J］. 航空学报， 2018， 39（5）： 321958.

Fang Ke， Zhang Qingzhen， Ni Kun， et al. Time-Coordinated Reentry Guidance Law for Hypersonic Vehicle［J］. Acta Aeronautica et Astronautica Sinica， 2018， 39（5）： 321958.（in Chinese）

［12］ 张晚晴， 余文斌， 李静琳， 等. 基于纵程解析解的飞行器智能横程机动再入协同制导［J］. 兵工学报， 2021， 42（7）： 1400-1411.

Zhang Wanqing， Yu Wenbin， Li Jinglin， et al. Cooperative Reentry Guidance for Intelligent Lateral Maneuver of Hypersonic Vehicle Based on Downrange Analytical Solution［J］. Acta Armamentarii， 2021， 42（7）： 1400-1411.（in Chinese）

［13］ 姜鹏， 郭栋， 韩亮， 等. 多飞行器再入段时间协同弹道规划方法［J］. 航空学报， 2020， 41（S1）： 723776.

Jiang Peng， Guo Dong， Han Liang， et al. Trajectory Optimization for Cooperative Reentry of Multiple Hypersonic Glide Vehicle［J］. Acta Aeronautica et Astronautica Sinica， 2020， 41（S1）： 723776.（in Chinese）

［14］ Chu H Y， Li J， Dong Y， et al. Improved MPSP Method-Based Cooperative Re-Entry Guidance for Hypersonic Gliding Vehicles［C］∥MATEC Web of Conferences， 2017.

［15］ Liang Z X， Long J T， Zhu S Y， et al. Entry Guidance with Terminal Approach Angle Constraint［J］. Aerospace Science and Technology， 2020， 102： 105876.

［16］ 王少平， 董受全， 李晓阳， 等. 助推滑翔高超声速反舰导弹多方向协同突防可行性研究［J］. 指挥控制与仿真， 2017， 39（2）： 55-60.

Wang Shaoping， Dong Shouquan， Li Xiaoyang， et al. Feasibility Study of Multi-Direction Coordinated Penetration of the Boost-Glide Hypersonic Anti-Ship Missile［J］. Command Control ＆ Simulation， 2017， 39（2）： 55-60.（in Chinese）

Collaborative Trajectory Planning Method for Hypersonic Glide Vehicle

Wang Xinyu1，Liang Xuezhi1，Shi Rui2，Zhang Dong1*

（1. School of Astronautics， Northwestern Polytechnical University，Xian 710072，China；

2. Systems Engineering Research Institute，China State Shipbuilding Corporation Limited，Beijing 100081，China）

Abstract： In order to meet the time and angle requirements of hypersonic glide vehicles cooperative reentry， a multi-constraint cooperative reentry trajectory planning algorithm is proposed considering the process constraints and transition point constraints. Time constraints and angle constraints are decomposed to vertical plane and horizontal plane， and Newton iteration method is used to plan drag acceleration-energy profile to achieve the longitudinal trajectory satisfied time and distance constraints. The sequential quadratic programming method is used to search the heeling angle turning point to make the trajectory terminal satisfy angle constraints. Through multiple iteration updates， it can get three-dimensional trajectory satisfied the constraints of time and angle. On this basis， this paper analyzes the flight capability of a single aircraft， and gives the determination method of the coordination parameters. The numerical simulation results show that the proposed method can be applied in various scenarios such as cooperative strike and cooperative delivery， and can plan a three-dimensional trajectory with high time and high angle accuracy for aircrafts. This method has strong adaptability to the mission and can meet various constraints and cooperative requirements.

Key words：  hypersonic glide vehicle；collaborative reentry；trajectory planning；time collaboration；direction collaboration；collaborative strategy

收稿日期：2022-05-19

基金項目：国家自然科学基金项目（61903301）

作者简介：王新宇（1997-），男，内蒙古乌兰察布人，硕士研究生。

通信作者：张栋（1986-）， 男， 宁夏青铜峡人，博导， 副教授。