数学眼光的理论审视与培养建议
胡晋宾 刘洪璐
摘要:数学“三会”是指数学眼光、数学思维、数学语言,它们分别对应数学整个活动的从现实世界提升到数学世界、在数学世界内部推进、从数学世界回馈到现实世界三个发展样态,与数学核心素养(关键能力)、“四基”、“四能”都有对应关系。数学眼光就是在思维过程中,找到数学的元素,发现数学的主题,提出数学的概念,捕捉数学的关系,欣赏数学的美感,彰显数学的观念。数学眼光的教育意义在于,重视核心素养理念,强调应用和创新意识,瞄准数学直觉本领。培养数学眼光应该重视应用举例,关切发散联想,倡导数学阅读。
关键词:数学眼光;数学核心素养;数学“三会”
《普通高中数学课程标准(2017年版2020年修订)》(以下简称“2017年版课标”)在“课程性质”中提出,要“引导学生会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界”②。《义务教育数学课程标准(2022年版)》(以下简称“2022年版课标”)进一步发展了相关思想,明确提出“三会”主张,即“会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界”③;并把它们作为培养学生数学核心素养的重要指导思想,写进课程目標。作为一个较为新颖的学术名词,对一线教师来说,怎样理解数学眼光的
②中华人民共和国教育部.普通高中数学课程标准(2017年版2020年修订)[S].北京:人民教育出版社,2020:2。
③中华人民共和国教育部.义务教育数学课程标准(2022年版)[S].北京:北京师范大学出版社,2022:5-6。
内涵,怎样把握数学眼光的发生机制,如何认识数学眼光的教育意义,如何落实数学眼光的培养,是重要的课题。
一、数学眼光的理论审视
(一)数学眼光的内涵解读
2022年版课标虽然没有明确给出数学眼光的定义,但是描述了数学眼光的作用:“数学为人们提供了一种认识与探究现实世界的观察方式。通过数学的眼光,可以从现实世界的客观现象中发现数量关系与空间形式,提出有意义的数学问题;能够抽象出数学的研究对象及其属性,形成概念、关系与结构;能够理解自然现象背后的数学原理,感悟数学的审美价值;形成对数学的好奇心与想象力,主动参与数学探究活动,发展创新意识。”①
既然叫作“数学眼光”,多少和看见、观察等有关系。基于2022年版课标的阐述,数学眼光、数学观察实际上是同义的。为了方便理解,我们给出数学眼光的操作定义:“数学眼光主要指在现实与数学之间进行的思维切换,也即:立足知识储备,关涉活动经验,借助数学抽象和直观想象,从现实案例‘看到数学内涵,从数学内涵‘想到现实案例。”②数学眼光是双向的,即不仅有看到现实案例想到数学内涵的一个侧面,而且有看到数学内涵想到现实案例的一个侧面。
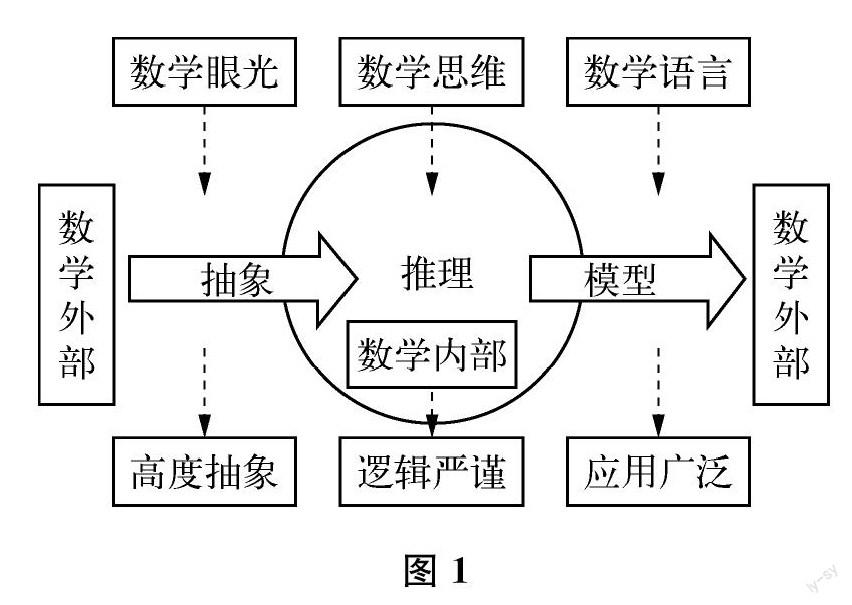
图1给出了“三会”与数学的基本思想(抽象、推理、模型)、特征(高度抽象、逻辑严谨、应用广泛)的大致对应关系。广义说来,数学是思维的科学。如果把思维当作动词,那么思维和思考等价,数学思维就是大脑内部的数学思考。从根本上说,无论是数学眼光(数学观察)、数学思维(数学思考)还是数学语言(数学表达),背后的内核都是“数学地思考”。只不过,如果把数学的整个活动分为从现实世界提升到数学世界、在数学世界内部推进、从数学世界回馈到现实世界这样三个发展样态的话,那么数学眼光对准的是第一个阶段,即从现实世界到数学世界这一跨越,不涉及后面的数学思维和数学语言分别对应的两个阶段。③
余秋雨先生指出:“文化,是一种成为习惯的精神价值和生活方式。它的最终成果,是集体人格。”④实际上,数学学习也是一个文化继承和学科熏陶的过程,就是形成数学观察、数学思考和数学表达的过程。因此,数学“三会”不同于语言课程的听说读写,迥异于科学课程的实验探索,有别于艺术课程的情感演绎。极而言之,数学“三会”就是带有数学气质、具有数学味道、体现数学特点的观察、思考和表达。数学眼光就是在思维过程中,找到数学的元素,发现数学的主题,提出数学的概念,捕捉数学的关系,欣赏数学的美感,彰显数学的观念。
(二)数学眼光与数学家眼光的异同
张景中院士这样描述数学家的眼光:“数学家看问题,关心的是数量关系和空间形式,用的是抽象的眼光。有些我们觉得不
①中华人民共和国教育部.义务教育数学课程标准(2022年版)[S].北京:北京师范大学出版社,2022:5。
②③胡晋宾,刘洪璐.数学眼光的内涵及培养[J].中学数学月刊,2021(2):17-20。
④参见:余秋雨.中国文化课[M].北京:中国青年出版社,2019。
同的东西,数学家看来却是相同的。3只小鸡、3只熊猫、3条恐龙,它们之间的差别可以使生物学家激动不已。但是对于数学家来说,无非都是干巴巴的数字‘3而已。月饼、烧饼、铁饼,到了数学家那里,无非都是圆。”①由此可见,数学家的眼光和前述数学眼光的概念本质上并无二致。数学知识是数学家群体创造出来的,学生学习数学,就是通过知识学习,培养出类似数学家的思维方式和思维本领。因此,我们认为,学生要培养的数学眼光与数学家审视问题时的眼光,在方向上是一致的,只不过学生的数学眼光形成是需要慢慢培养的,学习过程是漫长的,有高低深浅之分、进阶路径差异,不同的人在数与代数、图形与几何或统计与概率领域还有不同。
(三)数学眼光的素养对应与水平划分
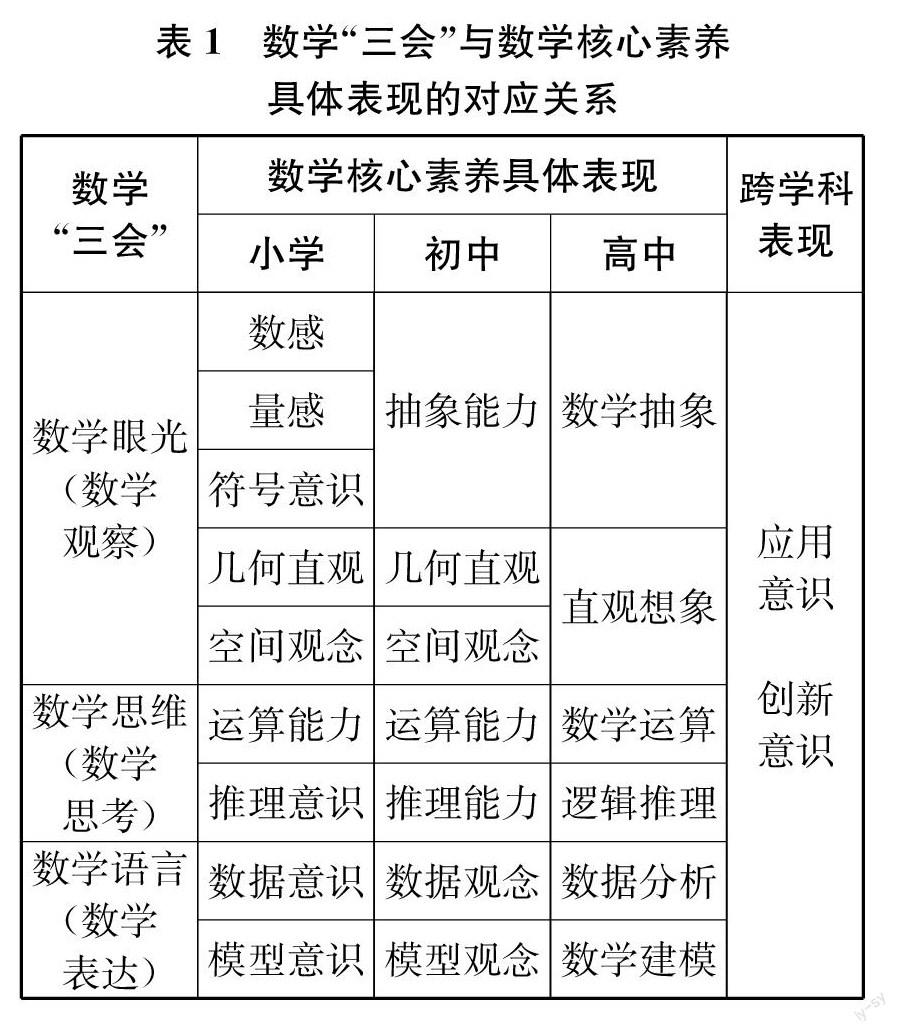
数学“三会”既是数学核心素养的终极性凝聚,也是数学核心素养的积淀后外化。具体地,根据2022年版课标和2017年版课标,数学“三会”与各个学段的数学核心素养具体表现的对应关系如表1所示。
数学是研究数量关系和空间形式的科学,考虑到义务教育数学常见的领域划分,数学眼光可以分为数与代数、图形与几何、统计与概率的领域差异,分别对应考察数量与数量关系、图形与图形关系、统计与统计关系。因为数学眼光是用来“观察现实世界”的,所以从现实世界的角度,可以划分为熟悉的情境、关联的情境和综合的情境三种水平层级。
(四)数学眼光的发生机制
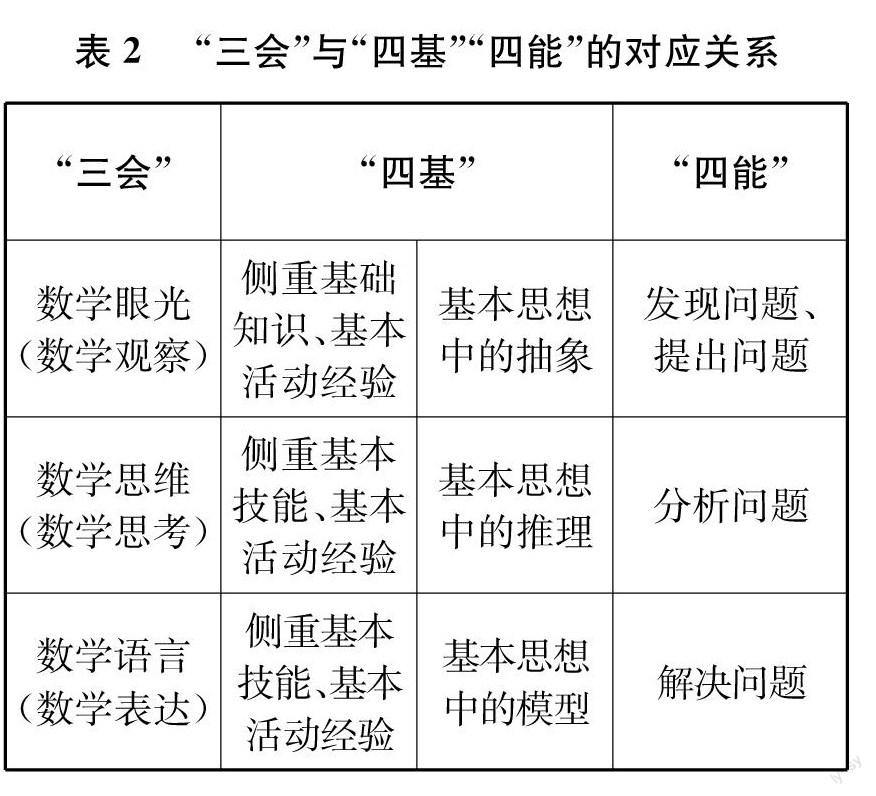
数学“三会”不仅和“四基”(基础知识、基本技能、基本思想、基本活动经验)有关,还与“四能”(发现问题、提出问题、分析问题和解决问题的能力)有关。如果把外部显性操作和内部思维操作都当作基本活动经验的话,那么它们的大致对应关系可以如表2所示。
数学眼光是在长期数学学习过程中练就的,需要数学基础知识和基本活动经验积淀的加持。从数学的视角发现问题和提出问题时,数学眼光就发生了。2022年版课标也在“教学建议”中指出:“要引导学生在发现问
①张景中.数学家的眼光(典藏版)[M].北京:中国少年儿童出版社,2011:42-43。
题、提出问题的同时,会用数学的眼光观察现实世界……”①
以看到兰州拉面场景想到幂指数知识为例,说明数学眼光的发生。看到拉面的根数在翻倍,这是一个数量关系模式识别的过程,于是大脑激活并提取出幂指数知识。因此,其中主要涉及既有的基础知识和基本活动经验。
(五)数学眼光的教育意义
1.重视核心素养理念
数学学习追求的不应该仅仅是冰冷的知识和量化的成绩,实际上,对于大多数人来说主要是一种“忘却”后留下的素养。提出“三会”理论并倡导数学眼光培养,可以改变数学高高在上、高不可攀的形象,因为在日常生活中就有“观察出来”的“活的数学”。
2.强调应用和创新意识
提出数学眼光的培养目标,意在侧重联系实际,强调学以致用和创新实践,反对死读书和“刷题”应试。比如,2022年版课标中有一个案例:如图2所示,左边为1个纸杯,右边为6个叠放在一起的纸杯,要求探究叠放杯子总高度的变化规律。②要从中直接“看出”函数来,确实需要数学眼光。设杯子底部到杯沿底边高为h(常量),杯沿高为x(常量),杯子个数为n(自变量),因此从初中数学的角度看,总高度H=h+nx是一次函数;从高中数学的角度看,显然可以把它看作一个等差数列(数列是一类特殊的函数)。
3.瞄准数学直觉本领
一般认为,数学思维包括数学的逻辑思维、形象思维和直觉思维三种形式。其中,形象思维、直觉思维与数学眼光关系最大。从根本上说,逻辑思维不能带来新颖创造和重大变革,仅仅是核准直觉思维的“卫生规则”;而直觉思维与合情推理,则是最富创意的思维形式与数学活动。数学眼光实际上是人们受过专业训练后形成的一种学科思维习惯和专业直觉。强调数学眼光,实际上就是强调这种直觉。仔细揣摩以下名言,不难体会直觉的重要性:
“逻辑和直觉各有其必要的作用,两者缺一不可。唯有逻辑能给我们以可靠性,它是证明的工具;而直觉,则是发明的工具。”(庞加莱)
“总应要求一个数学主题变成直观上显然,才可以认为研究到头了……”(F.克莱因)
“对于基本概念的理解,要变为直觉。”(杨振宁)
“猜测是一手货,需优先掌握;证明是二手货,可慢慢修炼。”(林群)
二、数学眼光的培养建议
前面已经述及数学眼光和“四基”“四能”的关系,数学眼光的培养显然和数学知识的不断累积有关,和数学思维的反复实践有关。除此之外,在日常学习和教学中,还应注意以下几点:
(一)重视应用举例
对于学生学习来说,一个经典的有趣案例,胜过一打花哨的蹩脚理论。③郑毓信先生在提到数学教师的基本功时,把善于举例作为第一项(其他两项分别是善于提问、善于比
①②中华人民共和国教育部.义务教育数学课程标准(2022年版)[S].北京:北京师范大学出版社,2022:84,178。
③张五常.吾意独怜才——五常谈教育[M].北京:中信出版社,2010:50-54。
较与优化)。数學教师应该善于通过精彩案例的列举,进行数学眼光的培养;应该善于借助教学世界的创设,架设生活世界和数学世界之间的桥梁。①教学时,不仅要让学生知道某个现实案例可以抽象成什么知识,而且要能反过来,给出相应知识,让学生列举出生活实例。
以初中三角形的稳定性为例,就有自行车撑子停车、空调外机安装固定、摄影器材三脚架支撑、太阳能热水器结构性焊接等案例。以高中周期性概念为例,就有历法计时、昼夜交换、四季更替、心跳反复、星期轮回、潮汐涨落、圆周往复、“离离原上草,一岁一枯荣”等案例。从这个角度来看,文理交融和学科交叉是应该提倡的。比如,从音乐、美术和体育等学科中看到数学的内涵,显然也是重要的数学眼光。
(二)关切发散联想
传统的数学教育强调演绎推理和数学运算,合情推理与数学直觉被认为是非主流的——再加上数学抽象与数学建模的被忽视,就存在“掐头去尾烧中断”的问题。实际上,后者是数学学习中不可或缺的一个侧面,应该得到同等重视。数学教学中,应该多引导学生发散联想,促使学生形成直觉,兼顾非逻辑思维发散的一面,改变数学刻板收敛的形象。
比如,林群院士就曾用吃薄饼等价于吃油条的例子,形象生动地揭示微积分基本原理的内涵:吃一定数量的薄饼(积分,求和)相当于吃若干根油条(微分,作差),而被积函数积分求面积的问题相当于原函数微分三角形中的求高。看似与数学风马牛不相及的吃早点问题,被轻松风趣地解读成了数学命题背后的深刻原理。
又如,我们在编写有关教材时,从以下生活中的多个案例抽象出变换及其对应的矩阵:(1)纹丝不动?恒等变换(矩阵);(2)弹簧拉伸?伸压变换(矩阵);(3)风车旋转?旋转变换(矩阵);(4)树木投影?投影变换(矩阵);(5)图像对称?反射变换(矩阵);(6)纸牌推移?切变变换(矩阵)。②显然,这也是数学眼光发散联想的具体体现。
(三)倡导数学阅读
数学眼光的培养,除了通过教材、通过教师教学之外,还特别需要注意引导学生加强数学课外阅读,以便扩大数学视野。数学教材好比正餐,当然需要重视,但是课外的数学科普阅读、数学讲座参与乃至数学新媒体学习等也是重要的学习路径。“汝果欲学诗,工夫在诗外。”仅靠数学教材学习或者数学解题,会窄化数学素养的形成,尤其是阻碍“三会”的培养。很多数学历史、文化、科普方面的阅读活动非常灵动活泼,能够激发学生的数学学习兴趣,逐渐帮助学生养成数学眼光。
(胡晋宾,江苏第二师范学院数学系,编审,博士。主要从事数学课程与教学论的教学及研究等。刘洪璐,南京师范大学附属中学。南京市优秀青年教师,曾获第五届全国青年数学教师优秀课展示活动一等奖。主要从事高中数学教学设计与研究等。)
①罗增儒.数学教育视角下的三个世界和四种数学形态[J].中学数学教学参考,2019(14):1。
②胡晋宾,刘洪璐,陈永高,等.普通高中课程标准实验教科书·数学(选修4-2):矩阵与变换[M].南京:江苏凤凰教育出版社,2008:12-35。

