问题提出理念引领下的数学游戏课教学

郭芬香

一、数学游戏课

“数学游戏”在《英国简明百科全书》中，条目是

“mathematical recreations”，定义为“利用数学知识的流行的娱乐活动”。我们把一些包含数学原理并使用数学知识或方法的游戏归类为数学游戏。这不仅是一场游戏，游戏中还包含着数学问题，因此玩游戏的人可以获得数学活动经验，并在不知不觉中掌握数学知识、思想和方法。

数学游戏课是借助益智玩具，以数学游戏为基本活动的学习过程。通过直观操作和数学推理，在学具的帮助下边玩边想，在动手实践中丰富活动经验，玩中学、做中思，培养学生的学习兴趣;在游戏中进行深层次的思维训练，培养学生的数学能力，启迪智慧，开发潜能。

二、问题提出

对于数学教育中的问题提出，蔡金发教授认为，应该是支持教师和学生的具体活动，使他们能够根据特定的情境（即问题背景或情境）形成或重新形成数学问题或任务。在这个定义中，蔡教授对“问题”或“任务”进行了更广泛的分析，包括任何可以提出的数学问题以及根据问题可以提出的任何数学任务。

三、基于问题提出的数学游戏课的基本结构

“基于问题提出的数学游戏课”指将问题提出理念运用于数学游戏课的教学中，通过提出问题，大胆猜想，实践操作验证或推理论证，解决问题，发展问题意识和创新能力。

四、“汉诺塔”游戏

教学目标：

第一，以“汉诺塔”游戏为载体，培养学生依据材料从不同角度提出数学问题的能力。

第二，孩子们在猜想、验证（操作、推理、规律）过程中解决问题，培养解决问题的能力，发展创新思维。

第三，借助數学游戏，激发学习数学的兴趣。

教学设计：

（一）利用传说，提出问题

“汉诺塔”游戏源于印度传说，却是法国数学家最先改编成数学问题并进行研究。对于传说本身，就包含着许多的问题因素。

1.阅读材料，形成问题

课始，教师出示文字材料：法国数学家爱德华·卢卡斯编写过一个印度的古老传说：在印度北部的圣殿里，三根宝石针被插入一个铜盘中。印度教的主神梵天创造世界的时候，在其中一根针从下到上穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个和尚在按照下面的法则移动这些金片：一次只能移动一片，无论在哪根针的上面，小片必须在大片上面。

学生看文字材料，独立思考写下自己认为和数学有关的1～2个问题。在自主提问阶段，经过独立思考之后，学生将相关数学知识内化，以达到个性化的学习状态。

【设计意图：以古老的印度传说引入，更能激发学生的数学学习兴趣，增加好奇心，对课堂学习充满期待。根据传说提出问题，需要学生先仔细阅读，提高学习的

效率。】

2.筛选问题，达成共识

在独立提问基础上，经过小组讨论，整理出最想讨论解决的3个问题。之后各小组派代表讲2个问题，层层筛选，共形成了以下9个问题：

（1）为何是3根针？

（2）为何是64片？

（3）为何一次只能移一片？

（4）为何小的要在大的上面？

（5）为什么法国的数学家要编写印度的传说？

（6）不按法则移动会产生怎样的后果？

（7）要移几次（多久）？

（8）为何叫汉诺塔？

（9）汉诺塔是谁发明的？

【设计意图：通过组内筛选，小组成员达成共识，剔除部分与本课学习关系不大的问题，使数学问题更集中指向本课学习，使问题更好地为本课教学服务。】

3.根据问题，分类整理

通过对数学问题的分类，抽象出问题的共性特点，从解决一个问题到一类问题进行延伸。

师：同学们有9个问题要解决，我们该怎么做才能系统地解决这么多的问题？

生：分类。

师：你认为这些问题可以分成几类？以小组为标准进行分类。

反馈后统一结果：计算类（7）;规则类（1、2、3、4、6）;其他类（5、8、9）。

【设计意图：在分类过程中探寻标准进行判断，在讨论、交流中不断修正思维，层层推进，发展了合作交流和语言表达能力。】

（二）依托问题，大胆猜想

在分类基础上思考计算类问题，体会不易。

师：第7个问题能解决吗？请你猜一猜到底要移

多久？

生1：应该要很长的时间。

生2：几亿次吧？反正很久很久……

【设计意图：在分类基础上进行猜想，让学生体会解决数据较大问题之不容易，从而用化繁为简进行解决。】

（三）合作探究，验证猜想

将复杂问题简单化，是数学学习的基本方法。运用规则操作验证，理解算理，在推理中寻找规律，最终解决问题。

1.实践体验，操作验证

根据移动规则，运用学具探索，增加活动经验。通过思考相关联步数，感悟规律。

师：想要解决这么复杂的问题，我们可以怎么办？

生：化繁为简，移一移汉诺塔，动手操作一下。

师：传说中是64片，老师提供的是5片，请你思考，该从几片开始研究？为什么？

生：从3片开始研究，2片很简单，只要3步（生移）;3片要移7步，要复杂些。

师：3片都会移吗？那4片要移几次？（生说15次）

师：同桌合作，1人移，1人记录，并仔细观察思考有没有移错。先移动3片，学生都会移了，再研究移动4片，请关注移动的次数，并思考移动3片和移动4片有什么关联？（2人合作操作）

师：谁能概括性地来说一说移动3片和4片之间有什么关联？

生：从移动3片到4片是3片的步数乘2再加1，师板书：7×2+1=15。

师：在移动过程中如何看出7×2+1？请在汉诺塔上演示。

生：先让3片移到中间杆要用7步，最大地移到目标杆加1步，最后把中间的3片移到目标杆又是7步（7+1+7），同时演示7+1+7的过程。

【设计意图：根据规则运用学具进行操作体验，在体验中感悟移动3片和4片之间的联系，突破难点，为寻找规律打下伏笔。】

2.回顾反思，推理验证

回顾课堂，在操作过程中积累了经验，通过推理，寻找汉诺塔的移动规律。

（1）在回顾交流中探寻规律

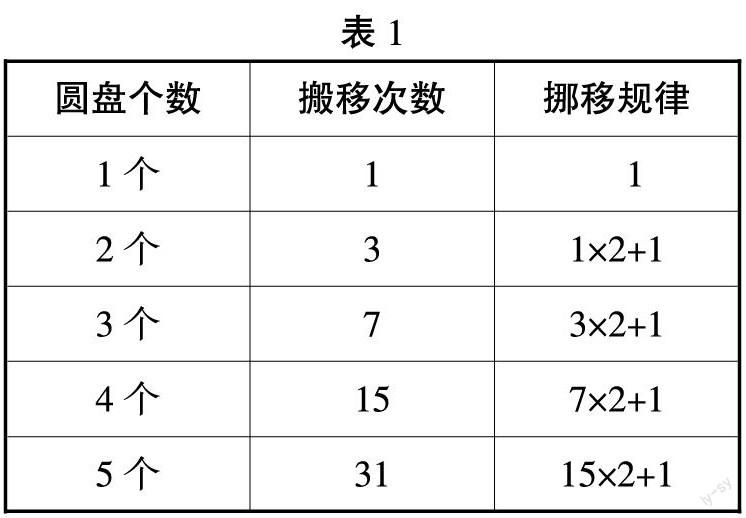
教师出示表格，根据表格，说一说移动5片要几次。（见表1）

如果教师把挪移规律稍微改动一下，你看得懂吗？5个圆盘该怎么表示？（见表2）

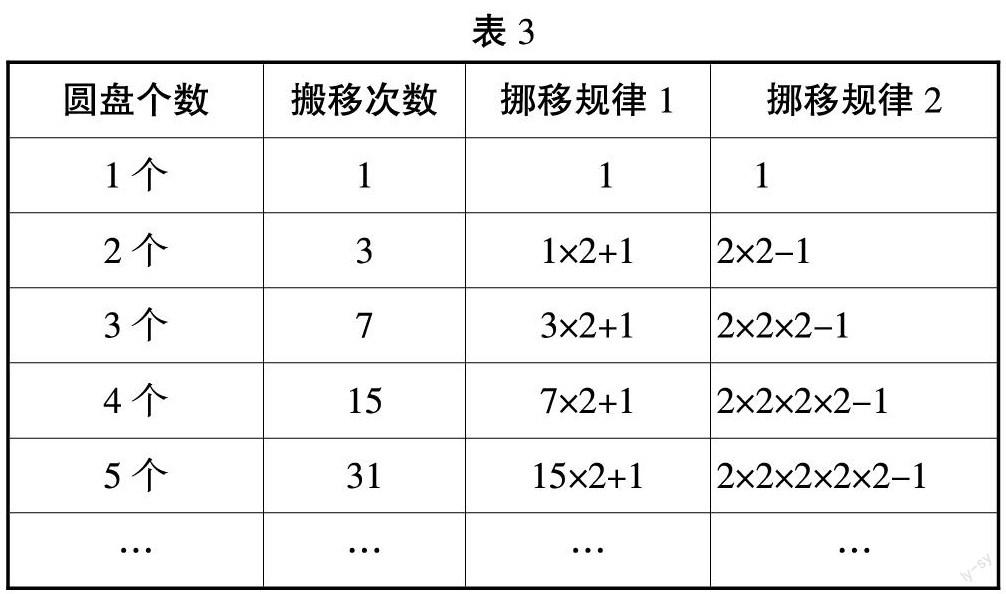
根据表1、表2，完成表3：

【设计意图：根据移动3个、4个圆盘的操作，在经验积累的基础上寻找搬移次数的规律。在规律探究中发现移动5个、6个，甚至更多个圆盘的移动规律。】

（2）在猜想估算中探寻规律

猜一猜移完20片要几次？学生猜后教师说，移完20片要100万次，同时出示表格（略）。

10个圆盘超过1000次，20个圆盘超过100万次，再猜，30个几次？

生：超过1亿。

师：对，100万后面大概还要加几个0？（学生说3个0）是的，30个圆片最少挪移1073741823次，超过10亿次，太不可思议了。PPT出示表格（略）

师：如果一天工作8小时，一秒挪移一次，30个圆盘要多久才能完成挪移？

师：先除以60变成分钟，再除以60变成小时，再除以24變成天，再除以365变成年，这些事情计算机已经算好。

一天工作8小时=28800秒

1073741823÷28800≈37283（天）

37283÷365≈102（年）

师：如果僧侣不休息地去做这件事，大概需要几年？（34年）

【设计意图：从移动10个到30个圆盘的移动次数，孩子们在猜想验证推算活动中体验30个圆盘的移动次数，进而体会完成这件事需要的时间有多漫长。】

3.依据材料，寻理论证

64个圆盘的移动规律，在学生现阶段还难以根据推理计算。在文字材料中寻求证据，进行论证。

师：再看一段文字材料。

斗转星移，梵天寺的僧侣们换了一代又一代，可是到现在那64个金盘子好像从来没移动过似的。为了那个神圣的誓言，僧侣们确实从来没有停止过工作，世界也依然很美好……时间一下到了20世纪40年代末的一天，大洋彼岸的一帮人搞出了电脑这个玩意儿，用电脑计算了移动64个金盘子所需要的时间：假如每次移动耗时1秒，移动64个盘子到第三根柱子需要的时间是264-1=18446744073709551615秒，换算成时间是5845.54亿年;看来僧侣们的任务任重道远，因为地球到目前为止才46亿年。

【设计意图：与前面的传说相呼应，更好地体现了汉诺塔传说的研究价值，使孩子们感受到编写神话者的

智慧。】

（四）课堂总结，明确目的

出示文字材料：提出一个问题通常比解决一个问题更重要，因为解决问题可能只是一种教学或实验技能而已。而提出新问题、新可能性并从新的角度看待旧问题需要创造性的想象力，这标志着科学的真正进步。

——爱因斯坦

【设计意图：发现并提出问题比解决问题尤为重要，从而激励孩子们提出更多的好问题。】

教后反思：

汉诺塔问题具有很高的研究价值，也是一种益智游戏。一般课堂都让学生根据游戏规则，寻找规律，解决实际问题，学会有条理地思考，获得成功体验这一路径开展教学。本课打破了教师原有的教学模式，在问题提出理念引领下，让学生经历提问问题、分析问题和解决问题的过程。真正在课堂教学中落实了动手实践、自主探究、合作交流这一课程理念。

（一）在问题引领中学习

拓展性数学游戏课程的教学目标不仅可以激发学生的学习兴趣，培养学生的动手操作能力和发展思维，还可以培养学生的创新意识。发现和提问是数学课程的目标之一，在教学中培养学生的课堂提问能力也是培养创造性思维的有效途径。在“汉诺塔”的教学中，利用传说这个载体，鼓励每个孩子提出问题。尽管一开始有的孩子提的问题对于本课的学习没有价值，但在提问的过程中孩子们积极思考，参与其中，真正体现了“不同的人在数学学习中得到不同的发展”这一课标理念。之后，教师筛选小组中的所有问题，并选择有价值的问题进行讨论和研究解决。在小组合作过程中培养合作意识，发展了批判性思维。在用汉诺塔操作活动时，又围绕核心问题“谁能概括性的来说一说移动3片和4片之间有什么关联？”引领学生进一步思考，从而发现移动规律。

（二）在互动交流中体现学生立场

促进学生有效提问的前提是坚持学生的地位，相信学生能够学习，构建宽容、尊重、和谐的师生关系和安全、温暖的课堂氛围。因为当你安全时，你会平静，当你平静时，你会明智。这是引导学生独立提问的生态基础。课始，教师让学生自主提问后，在组内进行互动交流，筛选有价值的问题，教师没有参与其中，这是建立在充分信任基础上的自主学习。实践证明，学生有能力对自己所提的问题进行甄选，及时放手调动了学生学习的主观能动性，发展了高阶思维能力。

（三）提出问题比解决问题更重要

学贵有疑，小贵则小进，大疑则大进。“怀疑”是人类打开宇宙之门的金钥匙，提出问题比解决问题更重要。从课中可以看出学生的问题非常多，筛选后还剩下一部分，一节课中没有办法全部完成。教师在和学生交流的过程中挑选了部分问题进行解决。正如课终所言“今天这节课我们提出了很多问题，也解决了很多问题，如果你能在解决问题后发现新的问题，当你解决的问题越多，那你提问题就会越来越难，每次想出新的问题，那新的可能性又要发生了。就像刚才有同学提到的第5个问题，印度人还只是当成一个传说的时候，法国人已经提出数学问题了。”这样的课堂培养的是学生创新思维能力，也是我们应该追求的目标。

五、启示

“汉诺塔”这一拓展性游戏内容，研究价值不仅限于益智，更能培养学生的创新思维能力。整堂课以问题引领着课堂方向和节奏，通过猜想验证，逐步迈向深入。因此，在数学游戏课中，运用问题提出理念进行教学，不仅能激发学生的数学学习兴趣，更发展了学生的创新思维，真正实现教学效益的最大化。

参考文献：

蔡金法，姚一玲.数学“问题提出”教学的理论基础和实践研究[J].数学教育学报，2019（4）.