强化百分数三大功能
屈婷

百分数不是数系扩充的产物,它多用于衡量一组数的特征,反映一组数据的总体情况。教学中,如何引导学生理解百分数的意义,体会它的应用价值呢?
一、巧设比较任务,凸显百分数的代表功能
百分数是描述一组数据的代表量。教学中,教师要创设合适的比较情境,引导学生体会百分数的产生源于数据刻画的需要,感受百分数的代表功能。
新课伊始,笔者创设了这样的情境:“学校准备举办运动会。六(1)班“定向投篮”项目有两名学生率先报了名。体育课上,老师帮他们测试了投篮成绩:小明投中3个,小强投中7个。谁的投篮成绩更好?”有学生认为:小强投中的个数多,小强成绩好。也有的学生反驳:如果小明只投了3次,3次都中了,但小强投了10次,只投中了7次,虽然小强投中的多,但投篮次数也多,这样比较不公平。笔者追问:只看投中个数还不够,你们还需要哪些数据?学生认为还需要看他们分别投了多少次。笔者给出以下数据“小明投了4次,投中了3个;小强投了10次,投中了7个”,并提问:现在可以判断了吗?学生用[34]和[710]分别表示两名学生的投篮成绩,并用通分的方法比较两个数的大小,得出小明的投篮成绩更好。
随后,笔者追问:[34]和[710]分别表示什么意思?比较这两个分数的大小就能反映出小明和小强的投篮水平了吗?学生通过讨论达成共识:小明和小强投的总次数不一样,投中个数也不一样,只比投中的个数不公平,要看投中个数是投篮次数的几分之几。笔者引导学生进一步思考:小军也想代表班级参加学校的定向投篮比赛,他的投篮次数是25次,投中个数是18个,与小明、小强相比,小军的成绩怎么样?学生发现:需要将三个分数统一单位之后才能比较,且以100做公分母比较合适。
在解决“谁投篮成绩最好”问题的过程中,学生逐渐认识到:百分数是为了刻画两个量的关系而产生的新数据,用它代表投篮命中率最合适。
二、探究来龙去脉,感悟百分数的表达功能
在解决问题的过程中,比较分数单位不同的两个量时需先借助通分的方法将其转化成单位相同的分数,再做判断和决策。
教学中,笔者这样引导学生感悟百分数在表达上的优势,体会百分数的独特价值。
师:我们比较3名学生的投篮成绩时,同学们都将分母统一成100,为什么要这样做?
生1:这样比较起来更方便。
生2:这样就有了统一的标准。将他们投篮的总个数都变成100,总个数相同的情况下,比较投中的个数就公平了。
生3:用100做标准,通分方便,计算也简单。
师:小轩也想参加选拔,他准备找体育老师测试成绩。你有什么建议?
生4:让他投10次,看能投中几次,这样容易比较;投25次也可以,这样通分更简单,容易比较4个人的成绩。
师:为什么要让他投10次或25次?
生5:人越多通分越麻烦,如果小轩投球的总次数较多,又不是100的因数,公分母会变得很大。
师:小轩投球总次数是40次,投中33个,小轩的成绩如何?在比较时用100作标准还合适吗?
生6:40和100的最小公倍数是200,用200做分母合适。
生7:[3340]可以写成[165200],如果分子和分母都除以2,用100作分母的话,分子就可以写成82.5%。
生8:分数好像不能这样写。
师:一般的分数的确不能写成这样的形式,但百分数可以写成分子是小数的形式,即写成82.5%。现在,你对百分数有什么新的认识?
生9:当要比较的人很多的时候,公分母会很大,把每个人的成绩都变成分数,计算很简单。
以上教学,笔者引导学生在比较中体会到百分数将100作为分数单位的优势——计算简单、便于比较。
三、借助深度对话,突出百分数的预测功能
百分数既可以用来刻画确定性数据,如利率、成分占比等,也可以用来表达随机数据。教学中,教师要引导学生经历用数据“说话”的过程,让学生体验解决问题方式的转变,突出百分数的预测功能。
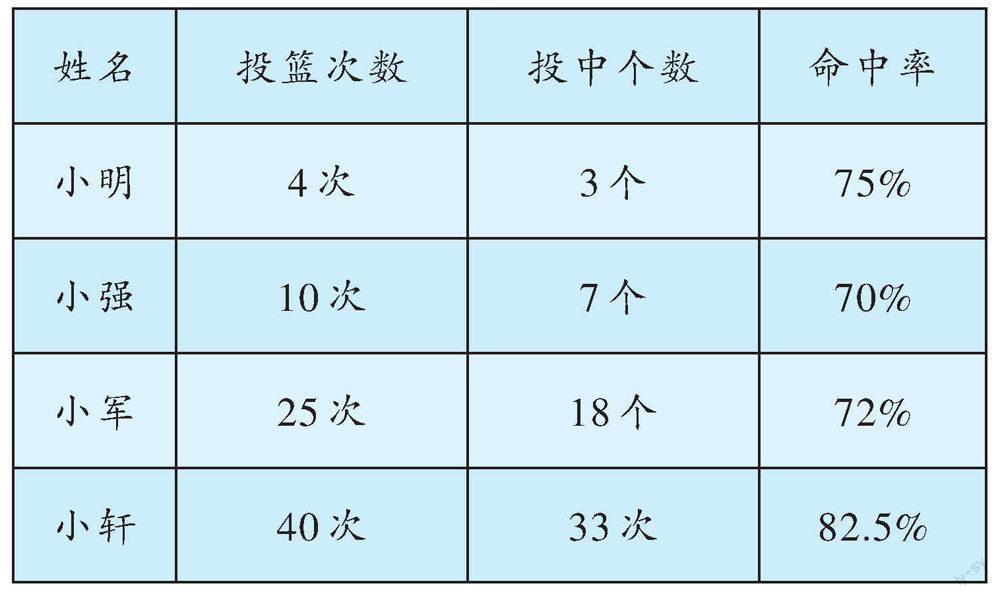
师:老师将从下表这4名学生中选2名参加学校的定向投篮比赛,你认为选哪2名学生比较合适?
[姓名\&投篮次数\&投中个数\&命中率\&小明\&4次\&3个\&75%\&小强\&10次\&7个\&70%\&小军\&25次\&18个\&72%\&小轩\&40次\&33次\&82.5%\&]
生1:小轩的命中率最高,小明的命中率第二,选小轩和小明参加最合适。
生2:小明的命中率虽然第二,但是他投的总次数少,可能会有运气的成分。
师:小明的75%是投篮多少次得到的数据?假如让小明再投4次,他的命中率还是75%吗?
生3:75%表示的是小明投了4次、投中3个,是用3除以4得到的。他再投4次,命中率就不一定是75%了。
师:体育老师让小明又投了4次,这次小明只投中了2个。现在命中率是多少了?
生4:投4次、投中2个,命中率只有50%。
生5:如果把两次放在一起算,投8次、投中5个,小明的命中率是62.5%。
生6:小军投了25次,命中率还能保持在72%,说明小军的成绩更稳定,应该選小军。
师:小明和小军,到底该选谁?
生7:让他们多投几次,谁成绩好选谁。
生8:小强投的总次数也比较少,应该给小强一些机会。
师:小轩的82.5%会出现波动吗?他的成绩还需要再测试吗?
生9:小轩的82.5%是投了40次得到的,波动不会太大,他可以不测试。
师:体育老师再次测试后,将小明和小强的成绩做了以下统计。
[姓名\&投篮次数\&投中个数\&命中率\&小明\&40次\&31个\&77.5%\&小强\&30次\&21个\&70%\&]
生10:小明投了40次,命中率还能保持在77.5%,说明小明还是有实力的。
师:这次我们决定选小明参赛和第一次想要选小明去参赛,有什么不同?
生11:第一次小明投篮总次数较少,有人觉得他达到75%的命中率是运气好;这次小明投篮的总次数是40次,命中率还能保持在77.5%,说明小明的确有实力。
生12:比赛次数少时容易出现特殊情况,得到的百分数没有说服力;比赛次数多一些,得到的百分数才能更好地代表一个人的实力。
学生以前解决问题的方式都是“确定的”, 但解决“选谁参加比赛更合适”这一问题所用的方法是“不确定的”。在根据命中率大小做决策的过程中,学生两次都选择了小明,但两次选择的理由是不同的。随着投篮次数的增多,学生逐渐体会到:数据越多,得到的百分数越稳定,越有代表性。
(作者单位:宜城市窑湾小学)
责任编辑 张敏

