人工智能专题类问题解析
楚小桃

人工智能博弈类问题求解中复杂的数理知识很难激发初中学生的学习兴趣,因此在教学活动中一般使用学生感兴趣的素材,深入浅出地解析问题求解。本文以田忌赛马、人鬼过河2 个典型的博弈类问题求解作为素材,开展关于编程思维的训练学习。
研究背景与意义
博弈问题是人工智能问题求解的研究内容之一,不论是问题求解还是博弈类问题都存在复杂的数理逻辑关系,它们既是现代数学也是统筹学的学习分支。比如罗马尼亚算法、递归函数、斐波那契数列、过河问题、汉诺塔等都属于问题求解。而田忌赛马、棋类游戏、囚徒困境等涉及“博弈”(含有对抗色彩)的竞赛等一般都属于博弈类问题。初中阶段,人民教育出版社在最新版本的《信息技术》教材中把人工智能部分的主题学习安排在九年级上册第2 章“人工智能与机器人初步”,问题求解是活动2“體验人工智能技术”中的学习内容。
概念引入与解析
问题求解是人工智能技术研究的重要领域之一。人工智能的许多概念,如规约、推断、决策、规划等均与问题求解有关。问题求解多数是通过棋类游戏、田忌赛马的故事展开引述的,在此使用实践探究活动帮助学生理解什么是博弈类问题求解,并将规约、推断、决策、规划等过程渗透到博弈类问题。博弈类问题涉及多种问题模型及其解决策略,借助人工智能可高效解决此类问题。
模型构建与推演
在田忌赛马故事里,齐威王和田忌双方各有上等马、中等马、下等马各1 匹。因田忌方各等级的马均不如齐威王,且每匹马只能参赛1次,田忌胜利的可能性不大, 孙膑献计田忌,最终田忌获胜。请问: ①孙膑有多少策略可以确保田忌完胜? ②齐威王完胜的策略有多少? ③谁获胜的概率更大? 具体是多少?
解题思路
规约 ①把各自的马分为3 个等级;②每匹马只能参赛1次。
策略 田忌采取上等对上等,中等对中等,下等对下等。
推断 田忌方各等级的马均不如对方,齐威王完胜。
问题求解 孙膑献计,田忌完胜,请问孙膑有多少策略可以确保田忌完胜?齐威王完胜的策略有哪些?
规划 用1 表示田忌方上等马,2、3以此类推;同理,用A 表示齐威王方上等马,B、C以此类推;可得到图1—图3。
分析 根据每匹马只能参赛1 次,按3 场竞赛的场次规则, 可以得到: 横向(A1-A2-A3、B1-B2-B3、C1-C2-C3)、竖向(A1-B1-C1、A2-B2-C2、A3-B3-C3)、三角组合(A1-B2-A3、A3-B2-C3、C3-B2-C1、C1-B2-A1、A1-B2-B1、B1-B2-C1、A1-A2-B2、B2-C2-C3……),以上组合皆不符合题意。
使用图表人工推演
回答问题 齐王获胜的策略组合有哪些?田忌获胜的策略组合有哪些?
决策 齐威王获胜的策略:A1-B2-C3、B1-A2-C3、A1-C2-B3、C1-A2-B3、C1-B2-A3。田忌获胜的策略:B1-C2-A3。
结论 齐威王获胜概率大,为5/6;田忌获胜概率小,为1/6。
田忌能在胜算极小的情况下获得胜利,与孙膑的谋略分不开。孙膑在熟悉规则后,能根据田忌具备的资源条件进行合理规划,并推演出所有可实施的策略与方法,最后进行决策,这个过程就是问题求解研究中典型的博弈类问题。
3匹马的模型一般学生均能无障碍地完成,出错率较低,使用数形结合方法完成效率较高。
扩大问题模型
解决多匹马问题前,应首先从缩减模型开始,假如双方各有1 匹马,学生得出齐威王必胜的结论,假如双方各有2 匹马,则会出现:齐威王获胜的策略是A1-B2,平局策略是A2-B1,田忌则完全没有获胜概率。然后扩大模型,让学生尝试人工作图推演:假如齐威王和田忌双方各有上等马和中等马,田忌还能获胜吗?假如齐威王和田忌双方的马匹数各增加到4、5、6、7、8、9……,再假如参赛队伍增加到3、4、5、6、7……,还能推演出田忌获胜的概率吗?增加马匹数后作图推演方法不再是简便方法,学生出错率非常高,教师通过设问让学生理解人工智能解决博弈问题的优势。
知识迁移
博弈类问题求解是进行思维训练的有效方法之一。博弈类问题求解也可以使用穷举法验证,人鬼过河问题就是入门级的穷举法验证过程。学生可尝试使用此法解决人工智能博弈类问题求解中的过河问题。
计算思维与算法
人鬼过河问题概述 3个人和3个鬼一同在A 岸,要把他们都运送到对岸B,只有1 艘船,船上最多只能载2个人(或者2 个鬼,或者1 人1 鬼〉,随意组合。但在同一岸的人数如少于鬼的数量,人就会被鬼吃掉(即任何一岸有2 鬼1 人,3 鬼1 人,3 鬼2 人都不行〉,从B 岸返回A 岸时必须有1人或1鬼划船,要把他们都运送到对岸B,至少需要多少步才能按要求过河。
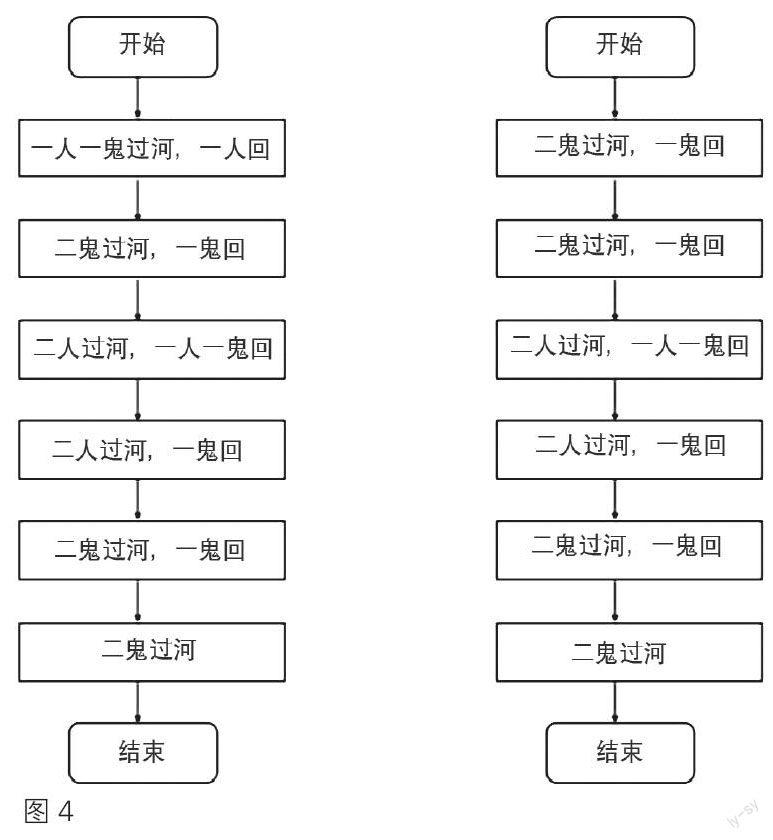
求解思路 可使用Excel 表格中的游戏试玩展开,试玩的过程其实就是试错的过程,也是通过穷举尝试多种不可能方法的过程,通过记录过程步骤,逐步改进方法,从而找到解决问题的最终方法,这个过程使用人工智能可以轻松解决问题,解法如图4所示。
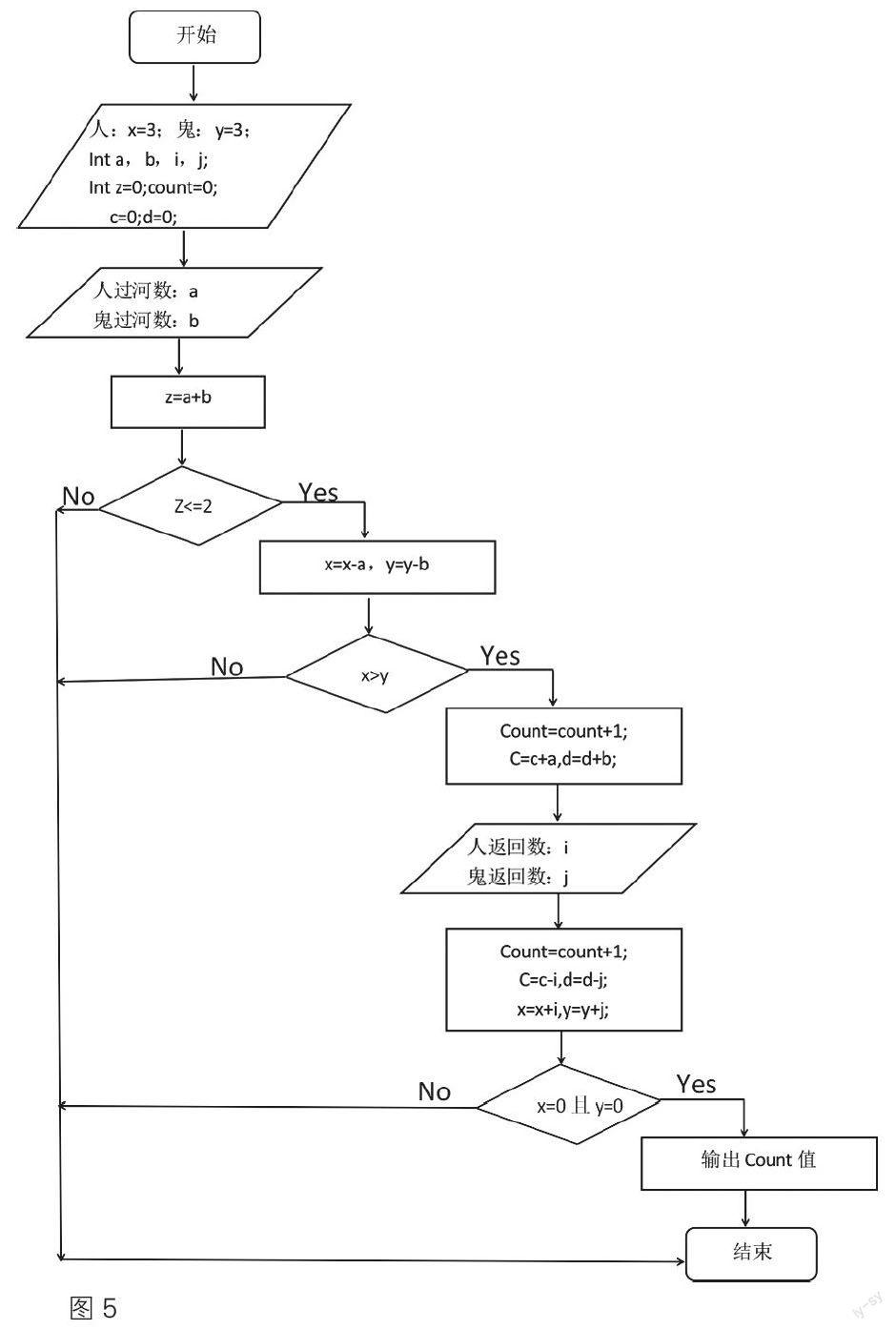
对于喜好编程的学生,教师也可以给出人鬼过河的程序流程图(图5),学生可以根据程序流程图选择使用图形化编程或其他人工智能语言编程。
总结反思与展望
博弈类问题求解需要在有限的时间内快速作出决断,可对人脑进行有意识的思维训练,不仅能让学生“知其然更知其所以然”地完成规约、推断、规划、决策的整个过程,还可以将其解析拆分成某个过程,譬如将规划单独抽出进行方法类的实践探究。最终完成由局部到整体,再由整体到局部的双向思维练习,有利于促进学生计算思维能力的提高。“田忌赛马”和“人鬼过河”这2个典型的博弈类问题求解,均以学生动手计算练习为抓手,重在提升学生的计算思维能力,让学生切身体会人工智能可有效提高解决问题的效能,深切地感受到人工智能超强的计算能力。

