含30°角的直角三角形在生活中的应用
程兰

在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半. 这个定理在生活中有着广泛的应用.
一、旧城改造
例1 某市进行“旧城改造”时,计划在一块如图1所示的三角形空地上种植某种草皮以美化环境,已知这种草皮每平方米a元,则购买这种草皮至少要().
A. 450a元 B. 225a元
C. 150a元 D. 300a元
解析:由∠BAC = 150°,能联想到30°角.
如图2,可作CA边上的高BD,
设与CA的延长线交于点D,则∠BAD = 30°,
由AB = 20米,即可求出BD = 10米,
然后根据三角形的面积公式即可推出△ABC的面积为150平方米,
已知这种草皮每平方米a元,则一共需要150a元.
故应选C.
二、轮船航行
例2 一轮船由东向西航行,在A处测得西偏北15°有一灯塔,继续航行20海里后到达B处,又测得灯塔在西偏北30°.如果輪船航向不变,则灯塔与船之间的最近距离是海里.
解析:如图3,过点P作PD⊥AB于点D,
则PD的长就是灯塔与船之间的最近距离,
易得∠APB = ∠PAB,可得BA = PB = 20.
根据含30°角的直角三角形的性质,可求得PD = [12]PB = 10.
故应填10.
三、超市滚梯
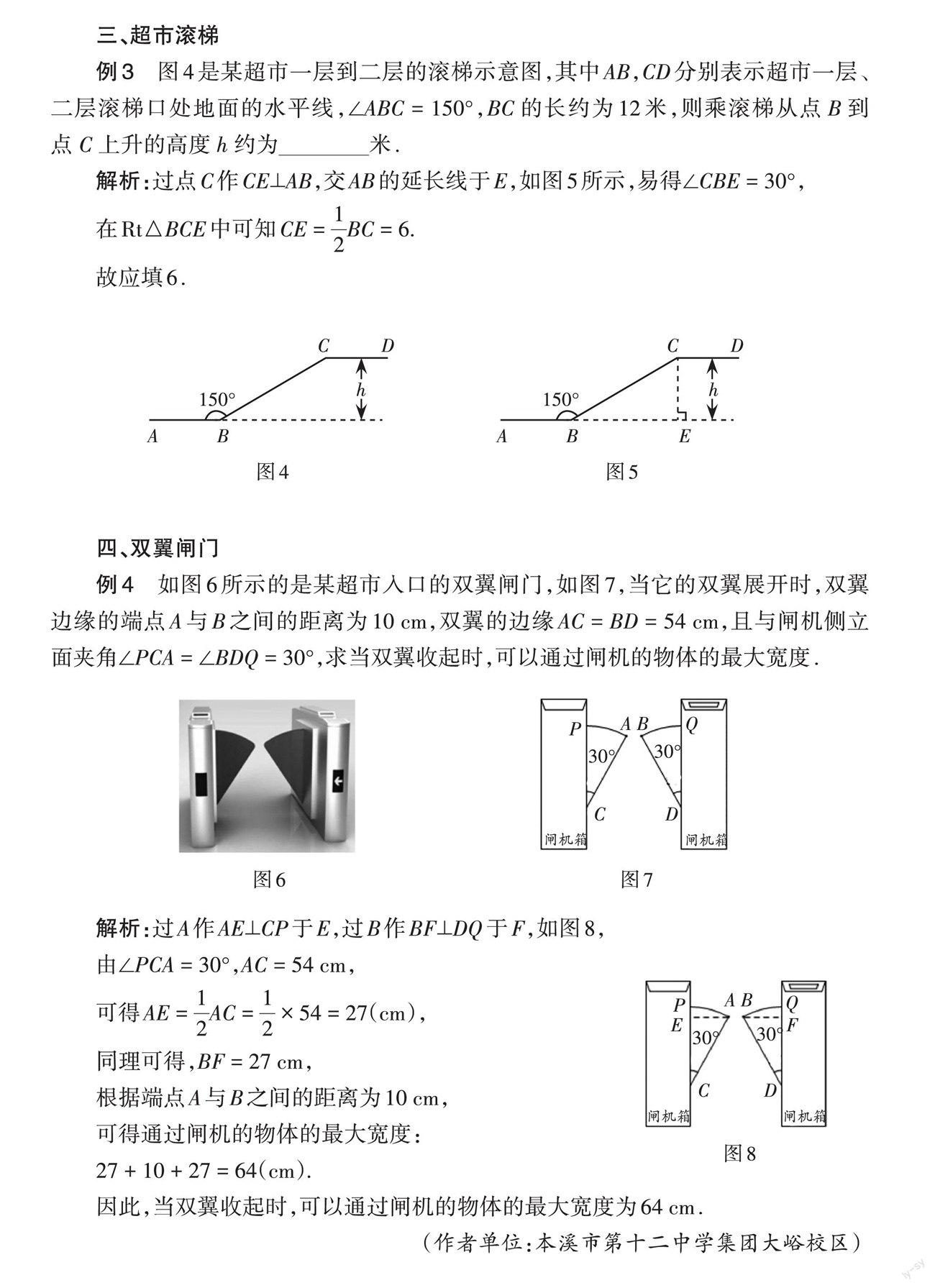
例3 图4是某超市一层到二层的滚梯示意图,其中AB,CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC = 150°,BC 的长约为12米,则乘滚梯从点 B 到点 C 上升的高度 h 约为米.
解析:过点C作CE⊥AB,交AB的延长线于E,如图5所示,易得∠CBE = 30°,
在Rt△BCE中可知CE = [12]BC = 6.
故应填6.
四、双翼闸门
例4 如图6所示的是某超市入口的双翼闸门,如图7,当它的双翼展开时,双翼边缘的端点A与B之间的距离为10 cm,双翼的边缘AC = BD = 54 cm,且与闸机侧立面夹角∠PCA = ∠BDQ = 30°,求当双翼收起时,可以通过闸机的物体的最大宽度.
解析:过A作AE⊥CP于E,过B作BF⊥DQ于F,如图8,
由∠PCA = 30°,AC = 54 cm,
可得AE = [12]AC = [12] × 54 = 27(cm),
同理可得,BF = 27 cm,
根据端点A与B之间的距离为10 cm,
可得通过闸机的物体的最大宽度:
27 + 10 + 27 = 64(cm).
因此,当双翼收起时,可以通过闸机的物体的最大宽度为64 cm.
(作者单位:本溪市第十二中学集团大峪校区)

