搭建思维平台 促进有序思考

姜素贞

［摘 要］对小学生来说，有序思考是一种极为重要的学科素养，这种思考问题的方式可以大大提高学生思考能力，对发展学生的理性思维大有裨益。有序思考是学生研究数学问题、掌握数学规律、应用数学定律解决问题的一种必备技能。因此，教师应该着力培养学生思维的有序性，有针对性地开展一些需要有序思考才能快速解决问题的活动。

［关键词］有序思考；对比；模型；列举

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2022）32-0082-03

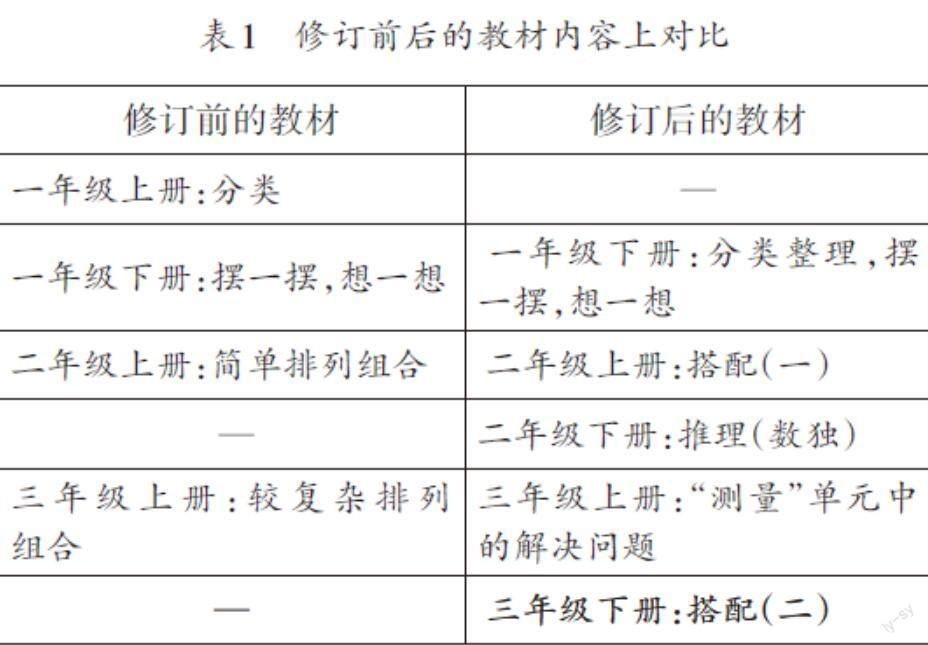
新修订的人教版教材大力开发了有序思考的强大功能，表1是修订前后的教材在有序思考内容上的对比。

通过对比，可以找出两点不同：关于有序思考的课程明显增加；新版教材专门列出一个关于有序思考的“解决问题”模块。因此，如何将有序思考植入问题中，切实提高学生有序思考的能力呢？对此，笔者选取了人教版教材第五册“测量”一章中新设的“解决问题”模块来“破题”。

一、创设情境，搭建支架

技能不是一朝一夕可以练就的，需要日复一日地苦练。尤其是低年级学生，他们以形象思维为主，对有序思考的认知必须借助直观演示，然后抽象出有序思考的过程。这就需要教师创设巧妙的情境，使有序思考具象化、可操作化。

【案例1】

师：我们已经知道，计量较重的物品时，应以“吨”作单位。现在我们就一起来解决有关“吨”的问题。（出示图1）

生1：用载质量为2吨的货车来运，需要运4次。

师：再仔细读题。假设你是运输公司的老板，你能设计一个让两辆车的司机都能接到派单的派车方案吗？

生2：我想到一种方案，可以让两个货车司机都能接到任务，那就是用载质量为3吨的货车运2次，还剩2吨煤，就用载质量为2吨的货车运1次。

师：你确定这是最佳方案吗？

生2：确定。

教师列出表格（如表2）。

师：看来，这道题对你们而言是小菜一碟。现在老师变换一下数据，你们试着解一解这道题。（出示图2）

师：要求不变，请列出所有方案。

【反思】教师大幅改动数据，提高难度，主要出于两点考虑：（1）尊重教材的原型问题“如何派车能恰好运完8吨煤”，这其中的关键词“恰好”，就已经排除了不能完成任务和浪费货运资源的情况，且“8吨”这一数据较小，解决时用不上有序思考；（2）教材的例题只是一个引言，引出基本的数量关系，之后的数据改动才是真章，因为数据一旦变大，学生就无法凭经验和直觉看出答案，有序思考就应运而生，学生在一一排查、手忙脚乱时，自然会设法寻找捷径——有序思考。其实，创设情境本身就是为学生的思维发展“搭梯子”。

二、对比体验，优化程序

通过“搭梯子”，学生感悟到有序思考的先进性。要让学生真正理解、掌握、运用有序思考，教师还需设计对比分析环节，帮助学生逐步构建起有序思考的数学模型，并优化模型结构。

【案例2】

出示生1的方案（如表3）。

师：谁来评价一下这位同学的方案？

生2：这位同学没有列出完整的方案。

师：没错，那么如何才能列出所有方案？

生2：必须按照某种顺序进行思考，一一列举，这样才能不重复、不遗漏。

教师出示生2的方案（如表4）。

师：如果说生1的思考是没有条理的，那么生2的思考过程含有某种顺序吗？

（其他学生都表示“有”）

师：从第一列的数据就可以看出有顺序，从10次到0次，一个不漏，那第二列数据是怎么来的？

生2：计算所得。

师：能试着举例揭示这些数据的含义以及运算过程吗？

生2：载质量为2吨的车运输10次，总共运了20吨，因此就不需要载质量为3吨的车去运，即运0次；载质量为2吨的车运输9次，已经运了18吨煤，余下的2吨就得让载质量为3吨的车单独运送1次，但是为了满足“装满”的硬性规定，因此装3吨煤，总共运21吨……

师：原来如此，只要列好了第一列的数据，就可以推算出第二列的数据，根据第一列的趟次预设，推算出已运送量和剩余量，然后将剩余量交由载质量为3吨的车来运，看看需要几次。

师：对于这种思路，其他同学有什么想法吗？

生3：老师，我认为有些数据没必要列出，比如写到第二行，当用载质量为2吨的车运9次后，就可以预判运送总量不是20吨，后面的数据没必要写。

出示生3的方案（如表5）。

师：对比生2和生3的思路，说说你的看法。

生4：其实他们的思路是一样的，只是生3列出的表格更简洁。

师：说明生3排除了大量方案，这样会不会造成遗漏呢？

生5：这倒不必多虑，因为运用了制胜法宝——有序思考。

师：你青睐哪种方法？说说你的理由。

生6：当然是生3的方法，简洁有力。

生7：既然有些数据不需要写出来，那么还可以将表格再缩减一些。

出示生7的方案（如表6）。

【反思】这一教学环节才是本课的精华，在对比中展现有序思考的先进性，同时积累有序思考的经验，不断优化有序思考的程序。首次对比，目的在于彰显有序思考的必要性，从只写出2种方案到列举全部方案，全靠有序思考打底；第二次对比则是为了排除不必要计算，已知载质量为2吨的车的运输次数后，需要計算出载质量为3吨的车的运输次数，只要熟记乘法口诀，就可以心算出结果，避免计算书写，直接跳过不可能方案，从较大数算起，再加上有序思考加持，那么表格就会变得简洁。

三、小结梳理，促进升华

从某种程度来说，大道至简，思维的最高境界就是简约。数学教学中，一种思维方式的渗透绝不会只在一节课内完成，而是通过长期的思维训练来显现数学本质，通过反思和回溯思维过程，促进学生思维的提升。

【案例3】

师：现在回看生7的表格，结合题意，你有什么新的收获？小组讨论。

生1：既然要满足“用两辆车运煤”的条件，那可以将表格再缩减（如表7）。

师：这类题可以借助有序思考，列举所有可能。其实所有的情况都可以用一个算式来表示，你知道是哪个算式吗？

生2：3×（）+2×（）=20。

师：没错，其实所有情况都包含在一个算式里，只要满足这个算式的情况都可行。另外，进行有序思考时，也需要从较大数据开始考虑。

【反思】现在提出“公倍数”这一概念为时尚早，但是可以提前渗透。事实也证明，这样的渗透可以加速学生对有序思考的掌握。尽管算式“3×（）+2×（）=20”是一个拓展内容，但在学生建立有序思考的参考模型时发挥着巨大作用。首先，用算式构建有序思考的模型，便于学生找出数量关系；其次，对学生来说，越简单的内容越好吸收，算式无疑是简洁有力的模型。

总之，关于小学生有序思考能力的培养是一项艰巨的任务，教师应积极创造条件，在日常教学中渗透有序思考的内容，让学生学会运用有序思考解决问题。

［ 参 考 文 献 ］

[1] 邱廷建.用有序思考的方法解决搭配问题[J].数学小灵通（3-4年级版），2021（Z2）：4-6.

[2] 张莉茹，张丽芳.数之序：《有序思考》教学片断与思考[J].中小学数学（小学版），2021（Z2）：78-80.

[3] 李世锋.让小学生的“数学思考”真实发生[J].基础教育论坛，2021（18）：65-66.

（责编 黄 露）