一种在LUC基础上改进的密码体制及其安全性分析

杜珍珍，周 同，陆正福

（1.铜陵职业技术学院，安徽 铜陵 244000；2.云南大学 数学与统计学院，云南 昆明 650091）

引言

LUC密码体制[1]是一种可以替代RSA的公钥密码体制，特别是其不存在乘法的封闭性，在用于身份验证时可以抵抗适应性攻击，所以此时它的安全性高于RSA。为了能使LUC 密码体制在实际中有很好的应用，许多学者对LUC密码体制进行研究[2]，设计快速算法，并利用其设计秘密共享方案及数字签名方案[3，4，5]。

本文通过引入盲因子，结合LUC与RSA密码体制，构造新的密码体制，使其计算量低于LUC 密码体制，接近于RSA 密码体制，又拥有LUC 密码体制可以抵御乘法攻击的特性。

一、预备知识

（一）Lucas序列及LUC密码体制[1，2]

Lucas 序列可定义为：选两个非负整数P和Q，构成二次式x2-Px+Q=0，其根为，其中D是方程的判别式，即D=P2-4Q，如果选P和Q，使，则Lucas序列可定义为:

对于Lucas 序列，公钥密码体制主要研究Vn(P,Q)，在此只研究Vn(P,1)

它有下面的两个重要性质：

性质1 设a，b为任意正整数，则有Va b(P,1)=Va(Vb(P,1) ,1)

性质2 设a，b为任意正整数，则有Vb(V a(P,1) ,1)=V a(Vb(P,1) ,1)

LUC密码体制的基本思想：

①取两个不同的大素数f,w（保密）

③随机选取整数e，满足

④计算d，满足，同时删除f和w（其中N,e为公钥，d为私钥）。

加密算法：C=Ve(P,1) modN

解密算法：P=Vd(C,1) modN

LUC密码体制的证明：

加密：由二次式x2-Px+ 1=0，设其特征方程的根为则有Lucas 序列性质得

解密:由二次式x2-Ve(P,1)x+1=0，设其特征方程的根为，则有方程根与系数的关系

（二）H-LUC密码体制的相关知识

1.H-LUC序列简介

定义 设P,k为正整数(P＞k)，构造序列

则有

性质3 设a，b为任意正整数，则有

性质4 设a，b为任意正整数，则有

证明性质3左边=(P-k)ab+k，右边=((P-k)b+k-k)a+k=(P-k)ba+k=(P-k)ab+k，即证等式成立.证明性质4由性质3得

2.H-LUC密码体制

取两个奇素数f和w（保密）。计算N=fw（公开），（保密）。随机选取e（公开），满足计算d，满足 （保密）。

构造LUC公钥体制表示如下：

公钥：N，e;私钥：d（陷门信息f，w）;P为小于N的一个正整数;

加密算法：C=M e(P,k)modN

解密算法：P=M d(C,k)modN

二、安全性分析

关于H-LUC密码体制的安全性分析：

（一）H-LUC序列和离散对数问题的计算关系

定理1 对于任意的（x为整数），可以找到一个正整数来构造H- LUC 序列，在多项式时间内，有

证明：因为，令r-k=g，设是由r,k产生的序列，则

定理2 对于任意的和由r,k产生的序列，对于正整数x，有在域GF(p)或GF(p2)中可以找到两个元素g和y，使在多项式时间内，z=Mx(r,k)=y+k和y=gx成立.

证明：设Mt(r,k)是由r,k产生的序列，

则z-k=(r-k)x，由，令r-k=g，则由定 理1，y=gx. 因此，对于任意给定的，在多项式时间内，我们在域GF(p)或GF(p2)中能找到依赖于r和k的两个元素g和y，使得y=gx。

定理3 如果一个算法AL在GF(p)上能够用来解决H-LUC 问题，那么在多项式时间内，算法AL在域GF(p)或GF(p2)上也能用来解决离散对数问题。

证明：对于任意给定的且对某些未知的正整数x，有y=gx，我们想在多项式时间内通过算法AL计算出x。对任意给定的g和y，通过定理1，在多项式时间内，可以找到两个正整数，构造序列Mt(r,k)，使得成立.由于AL 能用来解决H-LUC 问题，则可以用算法AL 去计算x，使Mx(r,k)=y+k=gx+k成立，因而满足y=gx。

定理4 如果算法AL′在域GF(p)或GF(p2)中能用来解决离散对数问题，则对于任意给定的，AL′能用来计算正整数x，使得在多项式时间内，成立。

从定理3 和定理4 可知，如果算法AL能解决GF(p)上的H-LUC 问题，则在多项式时间内算法AL也能解决GF(p)上的离散对数问题;另一方面，如果算法AL′能解决GF(p)或GF(p2)上的离散对数问题，则在多项式时间内，算法AL′也能解决H-LUC 问题。因此，我们得到的结论是，H-LUC 函数的计算安全问题在多项式时间内等价于一般的离散对数问题。

（二）若N=fw被因子分解，则H-LUC 并没有被攻破。

因为若f,w已知，则便可算出.

解密密钥d关于e满足：

故d也不难求得，但由于在设计密码体制时，P是公开的，k是保密的，所以此时明文并不能被恢复。因此H-LUC 的安全性不仅依赖于因子分解的困难性，还依赖于盲因子k。

（三）LUC 公钥体制的抗攻击性高于RSA，是因为采用Lucas 数列来取代RSA 中幂的产生，不存在乘法的封闭性，即对于MdLd=(ML)d，如果知道M、M dmodN、L和LdmodN，则在不知道d的情况下，ML和(ML)dmodN也能被计算出来.而LUC 不具有乘法的封闭性，故在用于身份验证时可以抵抗此种攻击.该方案中所使用的H-LUC 数列，也不存在乘法的封闭性，所以其在用于身份验证时安全性也高于RSA，且计算量低于LUC。

三、实验分析

（一）文章在Java 平台上，取随机数r的长度为2000 比特位，随机素数f，w都为1500 比特位，密钥k为3000比特位，分别测试LUC算法、H-LUC算法（Java库里的求模幂算法）、RSA算法（Java库里的求模幂算法）的运行时间.在此，文章通过实验来演示LUC密码算法与H-LUC密码算法和RSA密码算法的实现时间（见图1）。

测试平台：CPU Intel—T6600（主频2.2GHZ，双核），内存2G，操作系统Windows-XP。

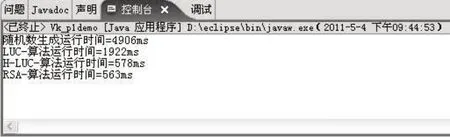
图1：算法运行时间比较

结束语

密钥管理是计算机网络中研究的一个热点问题，许多学者对其进行研究，主要从两个方面入手，一是减小计算量，二是增加安全性。LUC是一种可以替代RSA的密码体制，相比RSA公钥密码体制，具有能够抵抗共模攻击的优点，但其实现效率相对较低，文章结合RSA 与LUC 密码体制的特点构造HLUC序列，并给出其安全性证明。通过理论分析与实验表明，文章由H-LUC序列构造的密码算法运算效率高于LUC密码算法，略微低于RSA算法。