基于模型不确定性的保险人最优投资再保险问题研究

王雨薇, 荣喜民, 赵 慧

(天津大学数学学院，天津 300350)

0 引言

在现代保险实务中，由于激烈竞争，保险人一方面需要在金融市场中通过投资组合来盈利，以保证资金的保值增值；另一方面，又需要购买一定数量的再保险以规避巨额赔付风险，减小破产概率。因此，保险人的最优投资和再保险问题引起了学者的广泛关注。

破产概率最小化是保险人的重要目标之一，也是经典风险理论的核心问题之一。Browne[1]针对扩散风险模型，假设风险资产的价格过程服从几何布朗运动，证明了最小化破产概率和最大化期望指数效用对应的最优投资策略是等价的。此后，Hipp 和Plum[2]假设保险人仅投资于一种风险资产，基于复合Poisson 风险模型，研究了以最小化破产概率为目标的最优投资问题。Liu 和Yang[3]在Hipp 和Plum[2]的基础上，允许保险人投资于一种风险资产和一种无风险资产，但没有得到保险人投资策略的解析解。Yang 和Zhang[4]基于跳扩散风险模型，在保险人可投资于无风险资产和风险资产的情况下，对不同的索赔额分布给出了最小化破产概率的最优策略的数值解。Promislow 和Young[5]研究了扩散风险模型下以破产概率最小化为目标的最优投资问题。Bai 和Guo[6]在一支无风险资产和多支风险资产下，研究了以破产概率最小化为目标的最优投资再保险问题，得到了最优比例再保险和投资策略。Chen 等[7]在引入动态VaR 限制下，以最小化破产概率为目标，研究了最优投资再保险问题。Luo 和Taksar[8]考虑风险资产的投资限额，研究了以破产概率最小化为目标的保险人最优投资问题。Bai 等[9]采用二维复合Poisson 过程刻画相依风险模型，给出了最小化破产概率目标下保险人的最优再保险策略。

上述文献给出的模型参数基本上都是确定的，但在实际市场环境中却很难给出模型参数的准确判断。近年来，模型不确定性逐渐引起学者们的关注。Maenhout[10]研究了具有模型不确定性的投资组合问题，首次提出了鲁棒最优投资的概念。Lin 等[11]以及Zhang 和Siu[12]采用博弈论的方法，研究了含有模型不确定性的最优投资再保险问题。在Maenhout 工作的基础上，近年来很多学者研究了具有模型不确定性的投资-再保险问题。如Yi 等[13–14]在期望效用最大化和均值方差准则下分别给出了保险人的鲁棒最优投资-再保险策略。Sun 等[15]考虑方差保费准则和违约风险，得到了含有模型不确定性的保险人的鲁棒投资策略。Luo 等[16]考虑模型不确定性，得到了最大化目标实现概率下保险人的鲁棒最优策略。Young 和Zhang[17]考虑死亡力的不确定性，研究了最小化破产概率目标下的投资再保险问题。Li 和Young[18]考虑索赔发生率的不确定性，针对折现破产概率最小化的目标研究了保险人的最优再保险策略。

在上述文献中，风险资产的价格过程大多是用几何布朗运动(GBM)刻画的，即假设风险资产的价格波动率是确定的，而根据Beckers[19]、Campbell[20]、Hobson 和Rogers[21]等的研究，金融市场中风险资产的价格波动率是随机的。为了弥补GBM 模型的不足，Cox 和Ross[22]提出了常方差弹性(CEV)模型。作为GBM 的一个自然拓展，CEV 模型能够很好的解释波动率微笑等现象，近年来引起学者们广泛关注。Xiao 等[23]、Gao 等[24]研究了CEV 模型下的养老金投资问题，分别针对对数效用函数、指数效用函数和幂效用函数得到了最大化期望效用的投资策略。Gu 等[25]将CEV 模型引入最优投资再保险问题的研究中，Liang 等[26]、Lin 和Li[27]假设风险资产价格过程服从CEV 模型，研究了期望效用最大化目标下的保险人最优投资再保险问题。Gu 等[28]将风险过程作扩散逼近，研究了CEV 模型下保险人的最优投资和超额损失再保险问题。Li 等[29]假设风险资产的价格过程服从CEV 模型，研究了以乘积效用最大化为目标的保险人最优投资再保险问题。Li 等[30]和Zhao 等[31]基于均值方差准则，在CEV 模型下研究了保险人和再保险人的时间一致投资再保险策略。Zheng 等[32]假设风险资产的价格过程服从CEV 模型，在期望指数效用最大化目标下给出了保险人的鲁棒最优投资组合和比例再保险策略。A 等[33]和Wang 等[34]在CEV 模型下，研究了期望效用最大化目标下基于跳扩散风险模型的保险人最优投资再保险策略。

前述基于模型不确定性和随机波动的文献的控制目标主要集中在期望效用最大化和均值-方差准则，鲜有以破产概率最小化为目标的研究。Liu 等[35]首次研究了考虑模型不确定性的以破产概率最小化为目标的保险人的最优投资问题。本文在文献[35]的基础上考虑含有模型不确定性的以破产概率最小化为目标的保险人的最优投资再保险问题。假设保险人可以购买比例再保险，并投资于一个风险资产(允许卖空)。与文献[35]不同，本文假设风险资产的价格过程服从CEV 模型，使得所研究的问题更加符合实际。本文应用随机控制理论建立相应的HJB 方程，推导得到保险人的鲁棒最优投资再保险策略。最后通过数值模拟分析各模型参数对最优策略的影响。研究发现，保险人的模糊厌恶程度越高，其采取的投资再保险策略呈现出越保守的特点。本文的结构安排如下，第1 部分建立了投资与再保险模型；在第2 部分，我们应用动态规划原理建立了优化问题对应的HJB 方程，通过求解HJB 方程给出了鲁棒最优投资再保险策略和值函数的解析解；第3 部分给出了数值分析；第4 部分对文章进行了总结。

1 模型建立

假设(Ω,F,{Ft}t∈[0,T],P)为完备概率空间，其中F:=σ(F(1)∨F(2))，F(1)和F(2)分别是由布朗运动{W0(t)}t∈[0,T]和{W1(t)}t∈[0,T]生成的σ域流，P 为参考模型的概率测度。假设如下所有随机过程均是该概率空间上的适应性过程。保险和金融市场上交易是连续的，允许卖空，没有交易费用和税收产生。

1.1 财富过程

假设保险人的索赔服从带漂移的布朗运动

其中a、b为正常数，{W0(t)}t∈[0,T]为定义在完备概率空间(Ω,F,{Ft}t∈[0,T],P)上的标准布朗运动。保险人按期望值保费原理计算保费，则c0= (1 +θ)a表示保费率，其中θ>0 为保险人的安全载荷系数。根据(1)式，保险人的盈余过程满足

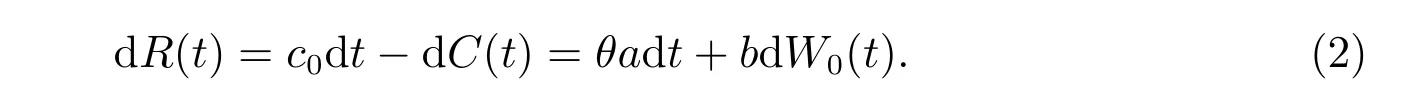
假设保险人可购买比例再保险或开展新业务(例如，作为其他保险人的再保险人，参见B¨auerle[36])以控制其保险业务的风险。对于任意时刻t ∈[0,T](T<∞)，保险人的风险曝露值为q(t)∈[0,+∞)。当q(t)∈[0,1]时，对应于保险人购买再保险的情形。在任意时刻t，保险人以c1= (1+η)a的费率购买再保险，其中η为再保险人的安全载荷系数且η>θ>0。对于每一笔索赔，保险人的自留比例为q(t)，即t时刻保险人自身只承担索赔额的100q(t)%，余下100(1−q(t))%的部分由再保险人承担。当q(t)∈[1,+∞)时，认为保险人开展了新业务。为了方便，后文将把保险人的风险曝露值q(t)称为保险人的再保险策略。考虑再保险策略后保险人的盈余过程R(t)可以表示为[()]

除了再保险以外，假设保险人可以将资金投资到风险资产上，假设t时刻保险人投资于风险资产的金额为π(t)，风险资产的价格过程S(t)服从CEV 模型

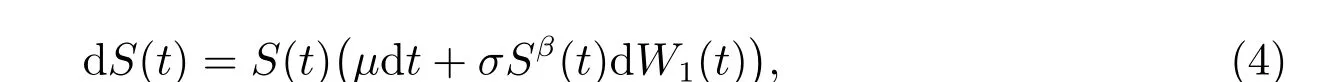
其中µ> 0，表示风险资产的回报率，σ表示风险资产价格的波动率，β称为弹性系数，σS(t)β称为即时波动率。{W1(t)}t∈[0,T]为定义在完备概率空间(Ω,F,{Ft}t∈[0,T],P)上的标准布朗运动，{W1(t)}t∈[0,T]与{W0(t)}t∈[0,T]相互独立。假设保险人的投资-再保险策略为α=(π(t),q(t))，则考虑再保险和投资后，保险人的财富过程满足如下随机微分方程

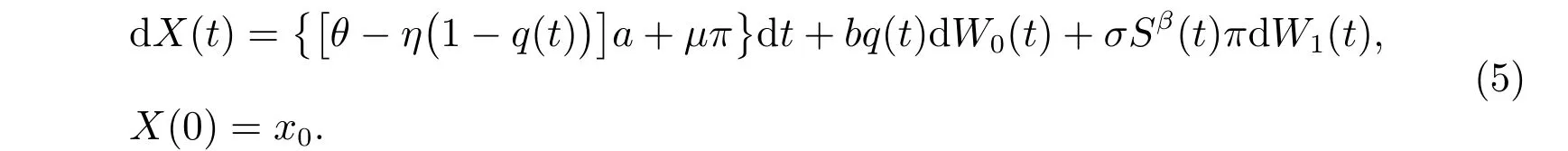
以上是传统的投资再保险模型框架，其中的保险人是模糊中性的。目前在保险精算领域有关破产概率最小化的文章，大多考虑的是模糊中立型保险人(Ambuguity-neutral Insurer, ANI)的最优投资再保险策略，即保险人完全信任现有的参考测度P。而事实上，很多投资者并不信任由参考测度描述的模型，为了更好地描述这种情况，本文考虑模糊厌恶型保险人(Ambuguity-averse Insurer, AAI)的最优投资再保险策略。由于模型不确定，AAI 在一系列备选模型中寻求稳健的最优投资再保险策略。备选模型与参考模型之间的差异通过不同概率测度之间的变换来体现。假设当前的参考概率测度为P，某一备选概率测度为Q，并且Q 与P 是等价的，则备选的概率测度集为Q={Q|Q∼P}。

基于上述假设，我们利用Girsanov 定理来变换概率测度，使得备选模型与参考模型仅在漂移函数方面有所不同。由Girsanov 定理知，对任意Q∈Q都存在失真过程

条件3)也被称为Novikov 条件。

根据Girsanov 定理，我们给出上述模型中的漂移项在等价测度Q 下的形式

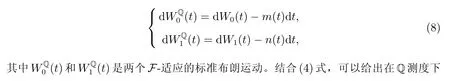
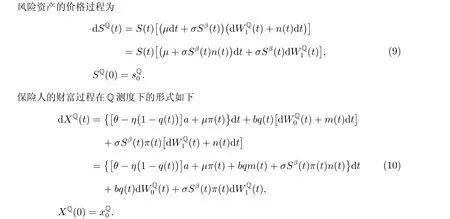
保险人引入备选模型描述模型不确定性，但备选模型与参考模型的偏离不应过大，因此引入相对熵的概念，作为备选模型偏离参考模型的惩罚项，来刻画备选模型与参考模型之间的差异

3) (π(t),q(t))使方程(5)有唯一的强解；

所有容许策略的集合用A表示。

1.2 破产概率最小化问题

保险人的目标是最小化破产概率，首先定义保险人的破产时刻

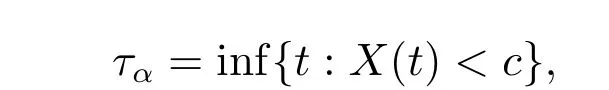
即保险人的财富水平首次小于阈值c的时刻。

注1 根据Webb[37]、Briys[38]、Gollier 和Wibaut[39]的研究，保险市场和金融市场存在相关性，在保险投资管理中不能将全部资产都用于风险投资，应划定一个比例g，将占总资产比例为g的部分进行风险投资和购买再保险，剩下部分作为储备金应对索赔风险。本文为了得到解析结果，通过引入阈值c设定保险人的财富最低值。即本文是将保险人的资产以阈值c划分开，留下c部分的资产作为储备金。由于仅依靠储备金不足以保证保险人的正常经营，因此，本文设定保险人的财富水平首次低于c时破产。

对于初始财富水平x，破产概率表示为

2 模型求解

本定理的证明类似文献[35]中定理3.1 的证明过程，这里不再赘述。

为了求解(15)式的鲁棒最优问题，只需要求解HJB 方程(17)。首先确定内层的模糊参数(17)式对m、n分别运用一阶条件

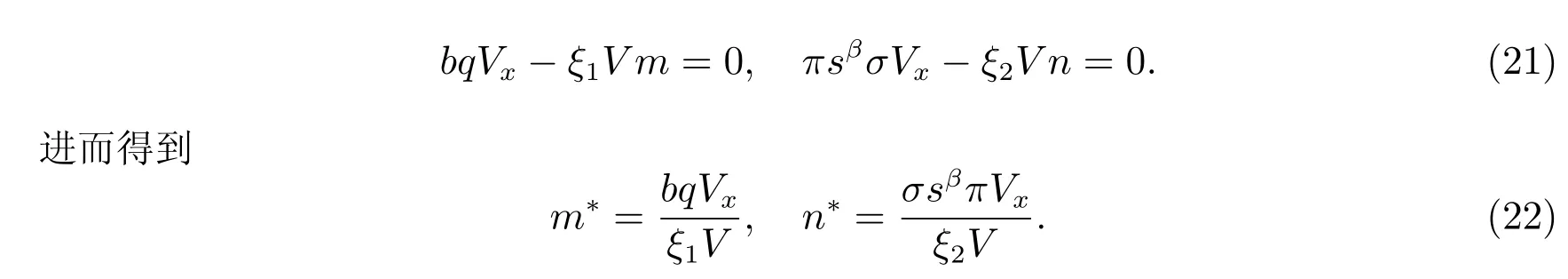
注2 为简化计算，这里将测度变换的失真过程{ϵ(t) = (m(t),n(t))|t ∈[0,T]}中的m(t)、n(t)记作m、n，将保险人的投资再保险策略α= (π(t),q(t))中的π(t)、q(t)记作π、q，将值函数V(x,s)记作V，后文计算过程中也将沿用该记号，不再做特殊说明。

2.1 β =0 的情况

当β=0 时，取q=0(不考虑再保险策略)，本文的CEV 模型退化为文献[35]中的模型。此时风险资产的价格满足几何布朗运动模型(GBM)

最优再保险策略q∗满足

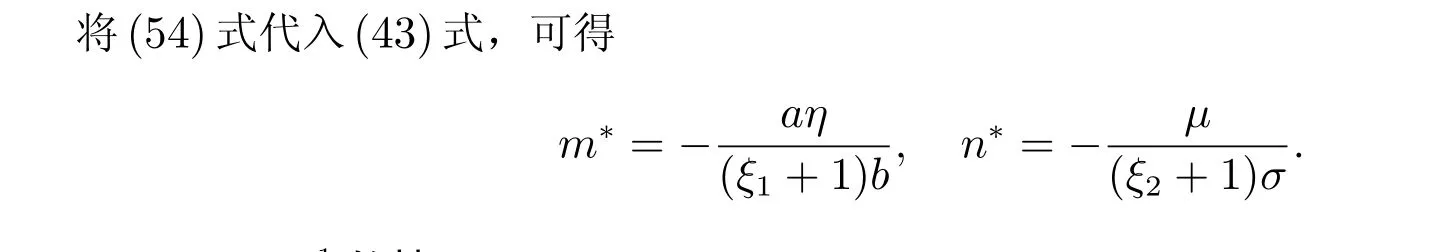
2.2 β =−12 的情况

注3 由于在实际市场中，一般认为风险资产的价格s是有界的，根据(64)式给出的值函数ψQ(x,s)的形式可以得到，ψQ(x,s)∈C2,2(R×R)。

2.3 不考虑模型不确定性的情况

当不考虑模型不确定性时，问题退化为在参考测度P 下的非鲁棒最优控制问题。在此种情况下，ANI 的财富过程满足(5)式，最优目标满足(13)式，对应的最优控制问题的HJB 方程简化为

3 敏感性分析与经济解释

本节主要给出最优投资再保险策略关于参数的敏感性分析和考虑模型不确定性与不考虑模型不确定性对应的最优策略之间的比较。除特别给出，参数均满足如下假设：a=1, b=1.5, θ=0.1, η=0.2, µ=0.06, σ=0.2, x0=10, c=4, s=3.5, β=−0.5。

3.1 模型参数对最优再保险策略的影响

3.2 模型参数对最优投资策略的影响

图2 给出了当β= 0 时，模糊厌恶系数ξ2和风险资产价格波动率σ对最优投资策略π∗的影响。上、下方曲面分别对应ANI 和AAI 的策略。我们发现，在考虑模型不确定性时，最优投资策略π∗与模糊厌恶系数ξ2正相关，与风险资产价格波动率σ负相关。ξ2越大，保险人对金融市场的模糊厌恶程度越低，在风险资产的投资上表现的越激进，即保险人将增加风险投资金额。而当σ增加时，风险资产价格的波动率增大，所以保险人将减少在风险资产上的投资。比较两个曲面发现，ANI 在风险资产上的投资金额高于AAI 的投资金额，说明AAI 的投资较ANI 来说更为保守。

图1 模糊厌恶系数ξ1 和再保险人安全载荷系数η 对最优再保险策略q∗的影响

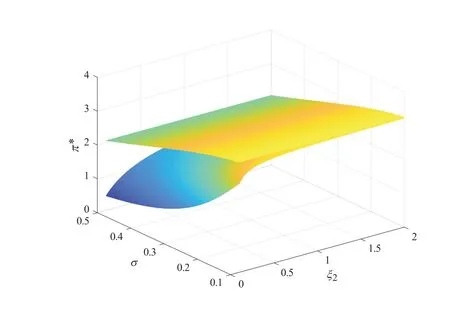
图2 β =0 时，模糊厌恶系数ξ2 和风险资产价格波动率σ 对最优投资策略π∗的影响

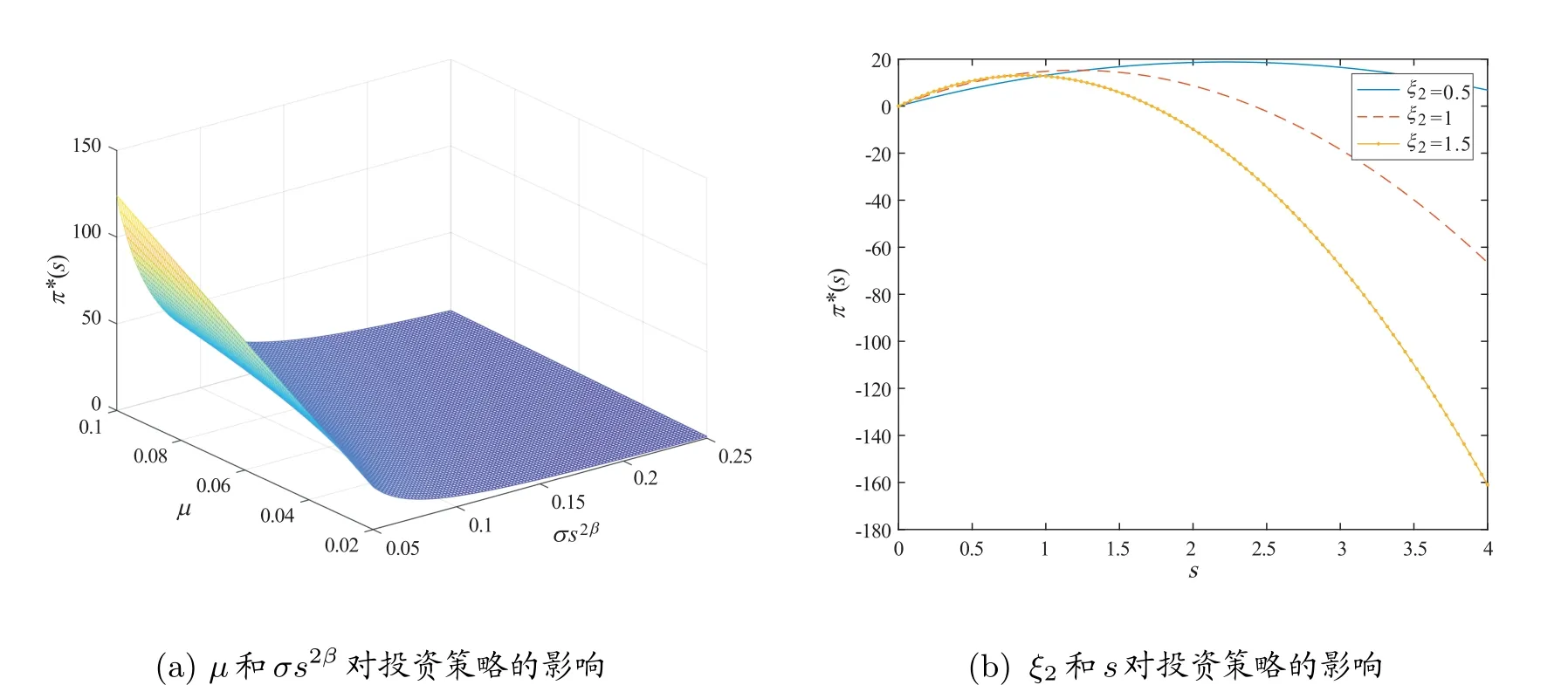
图3 β =−12 时，模型中相关参数对最优投资策略π∗的影响

3.3 模型参数对最优值函数的影响

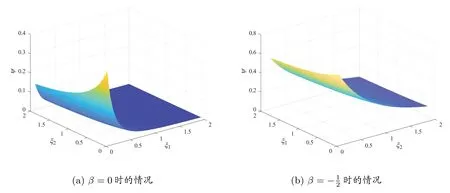
图4 模糊厌恶系数ξ1、ξ2 对最优值函数ψ∗的影响

3.4 模型参数对效用提升的影响

本部分将对AAI 考虑模型不确定性并采用鲁棒策略带来的效用提升进行分析。假设AAI 没有采用定理2 给出的鲁棒最优策略，而是采用2.3 节对应的非鲁棒策略代之，意味着AAI 在对参考模型存在模糊厌恶时仍然选择了ANI 的策略，这个策略是次优的，会带来一定的效用损失。下面我们先定义当AAI 采用ANI 策略时对应的值函数˜ψ(x,s)：

由于仅在β= 0 的情况下可以得到显示解，这里只对β= 0 的情况做分析。图5 给出了当弹性系数β= 0 时，模糊厌恶系数ξ1和ξ2对效用提升函数UI 的影响。发现效用提升函数为正值，意味着当模型存在不确定性时，AAI 采用鲁棒投资再保险策略会带来效用提升，降低保险人的破产概率。但对于不同的模糊厌恶程度，带来的效用提升效果不同。效用提升函数UI 随着模糊厌恶系数的增大而增大，意味着AAI 的模糊厌恶程度越低，对参考模型的掌握的信息越多，其采用鲁棒最优投资再保险策略的效用提升越明显。

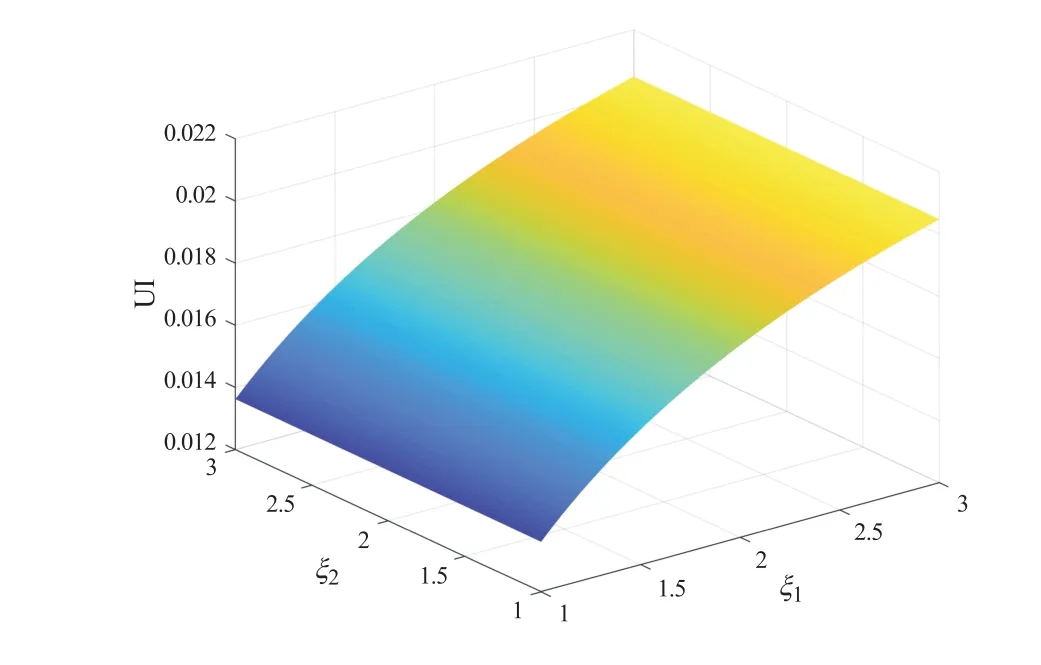
图5 模糊厌恶系数ξ1、ξ2 对效用提升函数UI的影响

4 结论

本文基于模型不确定性假设，研究了破产概率最小化目标下模糊厌恶型保险人的最优投资和再保险问题。保险人可投资于一种风险资产以实现储备金增值，同时购买比例再保险合约转移承保风险。文章采用扩散风险模型描述保险人的盈余过程，并用常方差弹性(CEV)模型刻画风险资产的价格过程。根据动态规划原理建立相应的HJB 方程，并针对不同的特殊弹性系数给出了保险人的最优鲁棒投资再保险策略和值函数的解析解，最后进行了数值分析来说明模型参数对最优策略和值函数的影响。

研究发现：

1) 保险人的模糊厌恶程度越高，其采取的投资及再保险策略越保守，对应的最优值函数越大，即破产概率越高；

2) 相较于AAI，ANI 的风险承受能力更高，采取的策略更激进；

4) AAI 的模糊厌恶程度越高，对参考模型的掌握的信息越少，采用鲁棒最优投资再保险策略的效用提升越明显。在未来的研究中，我们可以将模型进行推广，考虑在其他随机波动率模型下(例如：Heston 随机波动率模型下)的最优投资再保险策略，或者考虑保险人在更复杂的投资组合下的最优策略等。