基于S-DBR模型的生产排程研究
刘威,袁红兵
基于S-DBR模型的生产排程研究
刘威,袁红兵
(南京理工大学 机械工程学院,江苏 南京 210094)
生产排程方案的优劣对MTO型企业的生产效率影响较大。为缩短订单的平均处理时间、提高订单准交率,依托于约束理论(TOC)和“简化鼓-缓冲-绳子”(S-DBR)方法,通过计算产能负荷率识别内部瓶颈,以提高订单准交率为目标,构建了基于S-DBR方法的订单排程计划模型。设计排程问题的遗传算法,对遗传算法的个体编码、交叉和变异等操作进行处理,并以某电子产品生产车间为研究对象进行求解。结果表明,与传统人工排程相比,该方法能有效缩短生产周期、提高订单准交率。
TOC;S-DBR;生产排程
随着技术进步和市场环境的快速变化,客户对产品的要求变得越来越多样化和个性化,具体表现为产品的生命周期和交货期缩短。面对客户对订单交期越来越高的要求,Eli Schragenheim及H.WilliamDetttmer于2000年在“鼓”“缓冲”“绳子”理论(Drum-Buffer-Rope,DBR)的基础上提出了简化的“鼓”“缓冲”“绳子”理论(Simplified Drum-Buffer-Rope,S-DBR)[1]。S-DBR的关注焦点在于保证订单按时交货,提高客户满意度。国内外针对S-DBR的排程问题展开了广泛研究。Yung-Chia Chang等[2]将S-DBR应用于可重入流水车间,建立调度模型并进行仿真验证,新的调度模型能更好的反映订单紧迫程度,缩短生产周期,提高设备利用率及生产效率。Jun-Huei Lee等[3]讨论了S-DBR中产能受限资源(Capacity Constraint Resource,CCR)位置对计算投料时间和安全交期的影响、CCR漂移的情况以及插单问题,提出了计算投料日期、安全交期和缓冲状态的修正公式,分析了CCR漂移可能产生的影响,提出了使用订单的松弛时间来判断插单能否承接并安排插单生产的方法。张义[4]在DBR和S-DBR的基础上构建了新的生产管理模式,通过仿真验证,其在生产周期、在制品库存和有效产出这三个指标上优于传统S-DBR模式。文帅[5]针对瓶颈漂移问题对S-DBR模型进行了优化,通过设定锚定瓶颈、设置组装缓冲和界定资源共享原则,提出了S-DBR的优化模型,在识别和应对系统波动上有更好的表现。
上述S-DBR相关理论和技术在生产制造领域的研究和应用表明,S-DBR具有良好的交期保护机制,在排程方法上也更加方便可行。然而现有研究多针对特定问题对传统S-DBR模型进行优化,少有S-DBR在多品种小批量生产加工企业的实例研究。本文将S-DBR排程方法应用于某电子生产企业的生产车间,以订单准交率最大为目标,梳理S-DBR的排程逻辑,构建基于S-DBR的生产排程模型及其求解算法。并以该电子产品生产车间的生产数据为例,编制生产排程方案,验证排程方案的有效性。
1 基于S-DBR的电子产品生产排程方法
1.1 方法框架
S-DBR把市场需求视作生产系统的唯一瓶颈,生产系统的瓶颈不再属于内部,外部需求才是决定生产系统产出的关键环节。把原系统内部的瓶颈定义为CCR,通过对CCR上的负荷进行预测和监控来保证交期的可靠性[6]。在缓冲设置上,S-DBR认为,既然瓶颈位于外部市场,那么内部系统不再需要额外的瓶颈缓冲和装配缓冲,只需在控制内部生产的前提上,保留出货缓冲以应对交货的波动即可。故S-DBR仅一个缓冲,称为生产缓冲(Production Buffer,PB)。在排程计划上,S-DBR不再在瓶颈工序上进行详细的排程,只对投料工序进行排程,在CCR以及其他工序上则使用缓冲状态(Buffer Status,BS)来决定订单生产顺序。BS为订单从投料起所花费的时间与PB大小之比,反映订单的PB的耗用情况。BS越大,则表示订单的PB耗用越多,订单的交期剩余时间越短,交期压力越大,所以BS大者优先加工。在排程方法上,S-DBR使用计划性负荷(Planned Load,PL)作为依据来计算订单的投料日期和安全交期。PL即在某一排程计划期内,所有已确认订单的CCR负荷累积大小,用PL减去PB/2得到订单的投料日期,用PL加上PB/2得到订单的安全交期,如图1所示。
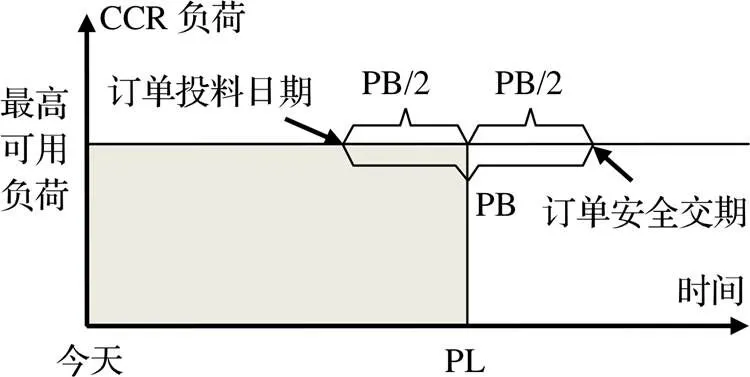
图1 投料日期与安全交期
投料日期即订单的投料日期,依据投料日期进行订单的投料准备,并按照该日期进行投料生产。安全交期即订单的可靠交期,依据安全交期判断订单是否能按时完成,安全交期表示该订单有把握完成的时间,若订单的客户交期大于安全交期,则在交期上可以接受该订单,反之则在交期上不能接受该订单。将订单客户交期与安全交期的差值定义为松弛时间,松弛时间的符号反映了订单能否在交期上接受的情况,松弛时间为正表示在交期上可接受该订单,反之则表示在交期上不能接受该订单。
与DBR相同,S-DBR也是通过“鼓”、“缓冲”、“绳子”来控制生产。市场作为整个系统的“鼓”,通过控制接单来管控生产节奏,订单的生产信息与生产系统内部的计划性负荷一起决定订单在投料工序上的排程顺序,并以此作为“绳子”传递信息;在投料工序到生产完成的整个过程中设置生产缓冲,即“缓冲”,作为排程依据之一,并用于预防系统波动带来的影响。在投料工序上按照排程方案安排生产,推动产品的整个生产过程,在投料工序以外的工序上使用缓冲状态来决定订单的生产顺序,并重点监控CCR上的生产状况,保证生产的顺利进行。S-DBR排程逻辑如图2所示。
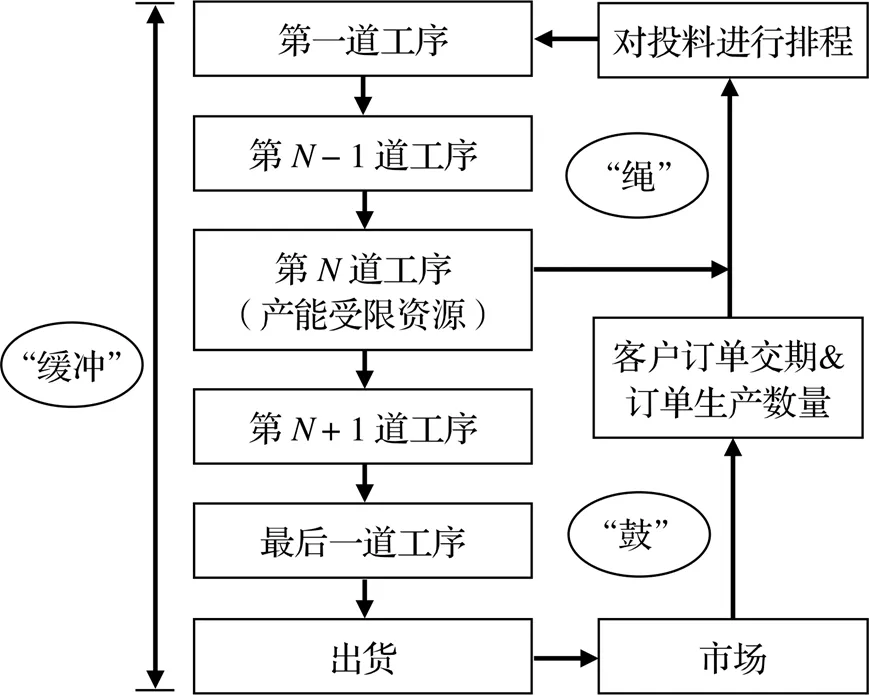
图2 S-DBR排程逻辑
1.1.1 产能受限资源的识别
S-DBR在排程时首先需要识别生产流程中的CCR,以便进行后续的计划性负荷、订单投料日期与安全交期的计算。S-DBR中的CCR本质上等同于DBR中的瓶颈工序,CCR可通过判断各个工序的产能负荷率来进行识别[7]。分别计算计划期内各道工序的生产负荷和有效生产能力,二者比值即为产能负荷率:
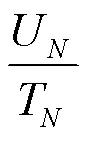
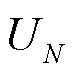
比较计划期内各道工序的产能负荷率,最大者即为瓶颈工序。
工序的生产负荷为计划期内所有订单在工序上的生产负荷之和,而每一个订单的生产负荷又包括产品加工时间与生产准备时间,即有:
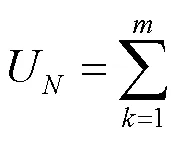
(N,k)=(N,k)(N,k)+(N,k)(N,k)(3)
式中:为计划期内工序上加工的订单数量;(N,k)、(N,k)、(N,k)、(N,k)、(N,k)依次为订单在工序上的生产负荷、生产数量、单件加工时间、生产次数、单次生产准备时间。
工序的有效生产能力由日有效生产时间与计划期内开班天数的乘积来衡量,而日有效生产时间由各道工序的日总工作时间扣除生产组织时间等,即为:
T=t(at-t-t)(1-r-r) (4)
式中:T为工序的有效生产能力;为单个班次的工作时间;t、t、t、t、r、r依次为计划期内工序上的开班天数、每日班次数、每日计划停机时间、每日生产组织时间、机器故障率和产品质量不合格率。
1.1.2 生产缓冲的设置
生产缓冲的定义是:一个最小可接受的批量,从投料到产出所花费的时间,包含了实际加工时间、等待时间、搬运时间、生产准备时间和预防系统波动的时间[8]。构建产品生产流程的仿真模型,模拟现实生产过程,以得到生产缓冲的大小。仿真模拟的方法具有方便快捷,成本低的优点,本文使用Witness仿真软件建立离散系统仿真模型,计算生产缓冲的大小。
1.2 排程模型及目标函数
取、(=1,2,…,;=1,2,…,)表示订单的编号和排程顺序,则在对订单进行排程时,每一个订单的编号和排程顺序信息用(i,j)表示。例如订单(3,2)表示计划期内排在第二位进行加工生产的是编号3的订单。若计划期内订单(i,j)进入排程,此时订单之前已有-1个订单排程完毕,则有:
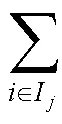
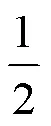
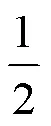
SLT=P-E(8)
式中:PL为计划性负荷;I={|为已经完成排程的-1个订单的订单编号};CCR为由产能受限资源识别模型得到的每个订单的产能受限资源生产负荷;S为订单的投料日期;PB为由仿真模拟得到的每个订单的生产缓冲;E为订单的安全交期;SLT为订单(i,j)的松弛时间;P为客户需求的订单交期。
SLT的符号可以判断订单是否逾期,排程的首要目标是提高计划期内订单的准时交付率。求解怎样排程使得订单逾期率最少的目标函数为:
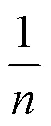
={SLT|SLT<0} (10)
式中:为订单数目;为松弛时间小于零的集合;||为有限集中元素的个数。
由式(5)~(7)可知,先排程订单会影响后排程订单的投料时间与安全交期,故该排程问题为NP(Nondeterministic Polynomially,非确定性多项式)问题。NP问题的求解方法多样,有启发式算法、智能优化算法、人工智能等[9]。本文采用智能优化算法中的遗传算法进行求解。最终得到排程流程如图3所示。
1.3 遗传算法设计
遗传算法首先是初始化一个种群,然后根据适应度函数确定个体的适应度,由适应度来选择个体进行交叉,再以某种概率让个体进行变异,从而不断选出适应度高的个体,进而更新种群[10]。遗传算法计算流程如图4所示。
1.3.1 个体编码
个体编码采用整数编码,取长度为的数字串,串中数字互不重复,取值范围为[1,]之中的整数。每一个数字串代表一个个体,个体中数字串里的数值大小表示订单的编号、出现的位置表示该订单的排程顺序[11]。例如个体(1 3 2 5 4 6 8 7)中数值3所处的位置是二,表示编号3的订单排程顺序为二。使用该编码方法的好处是能够直观反映订单的排程顺序。
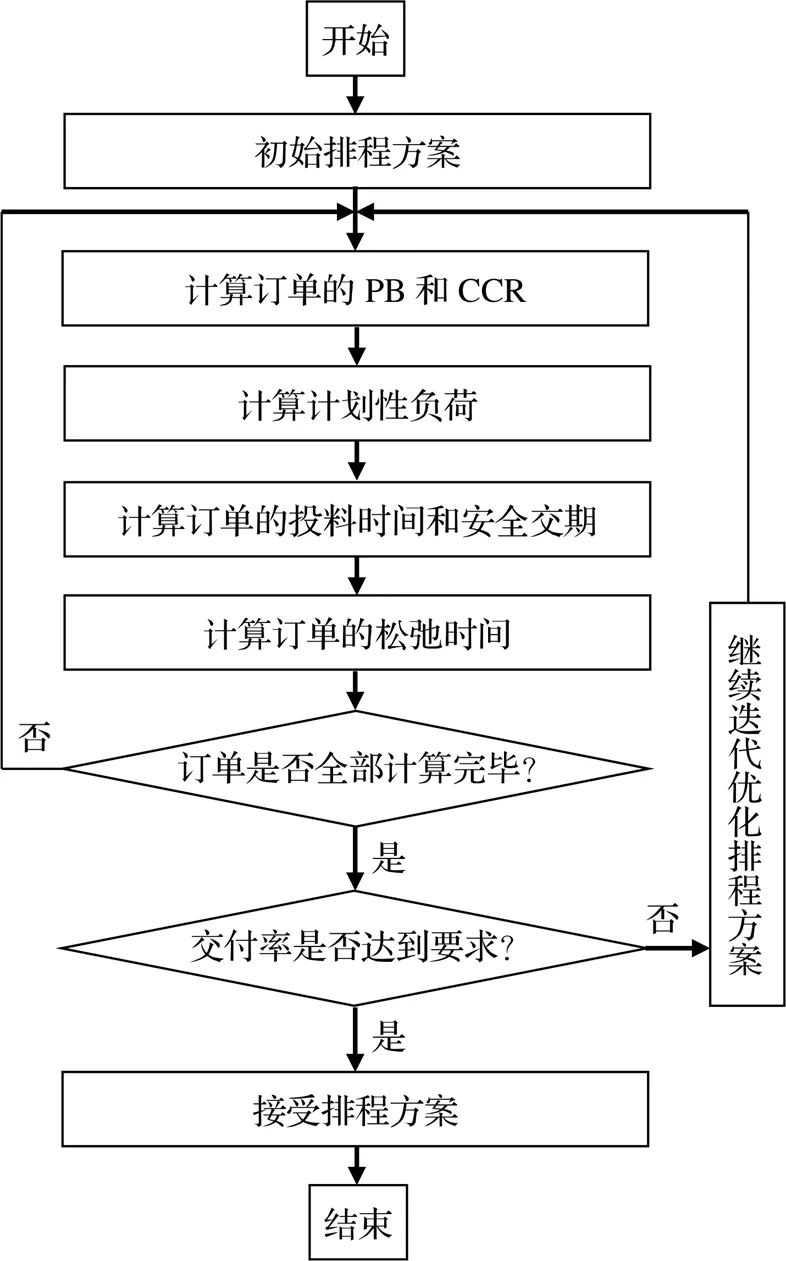
图3 S-DBR排程流程
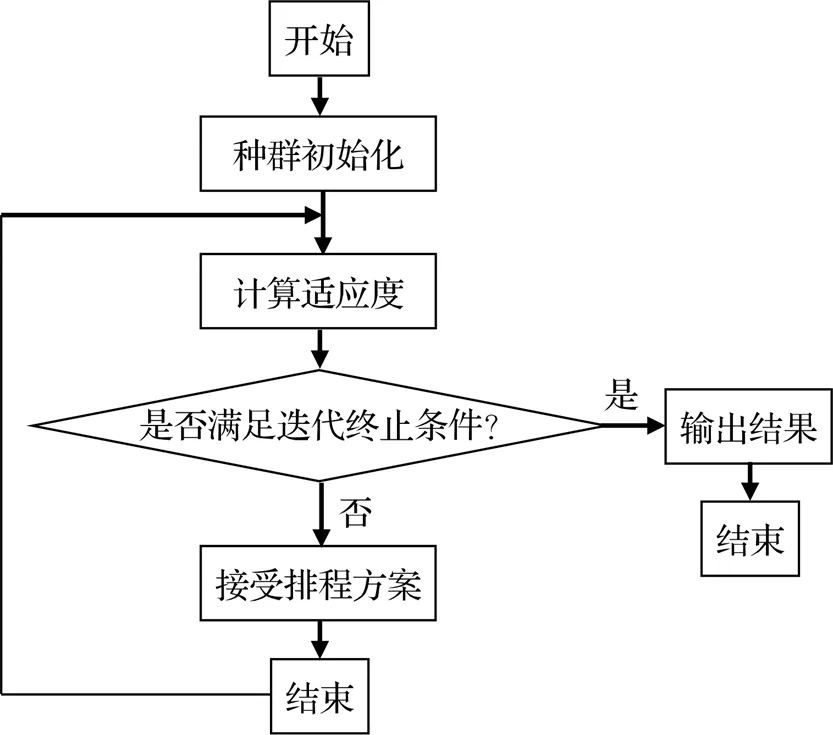
图4 遗传算法计算流程
1.3.2 初始种群
令种群中有个个体,则随机生产个长度为的数字串构成初始种群。
1.3.3 适应度计算
由于个体的编码反映了订单的排程顺序,所以每一个个体即是一个排程方案,求解过程中的目标函数值就可以评价排程方案的好坏,故本文使用目标函数来构建适应度函数。由于目标函数是求最小值,目标函数值越小说明排程方案越优、个体适应度值越大,故取目标函数值的倒数为适应度函数[12]。
1.3.4 选择操作
利用轮盘赌规则对种群中的个体进行选择,适应度值越大则被选择的概率越大。
1.3.5 交叉操作
本文中的交叉操作具体步骤如图5所示。
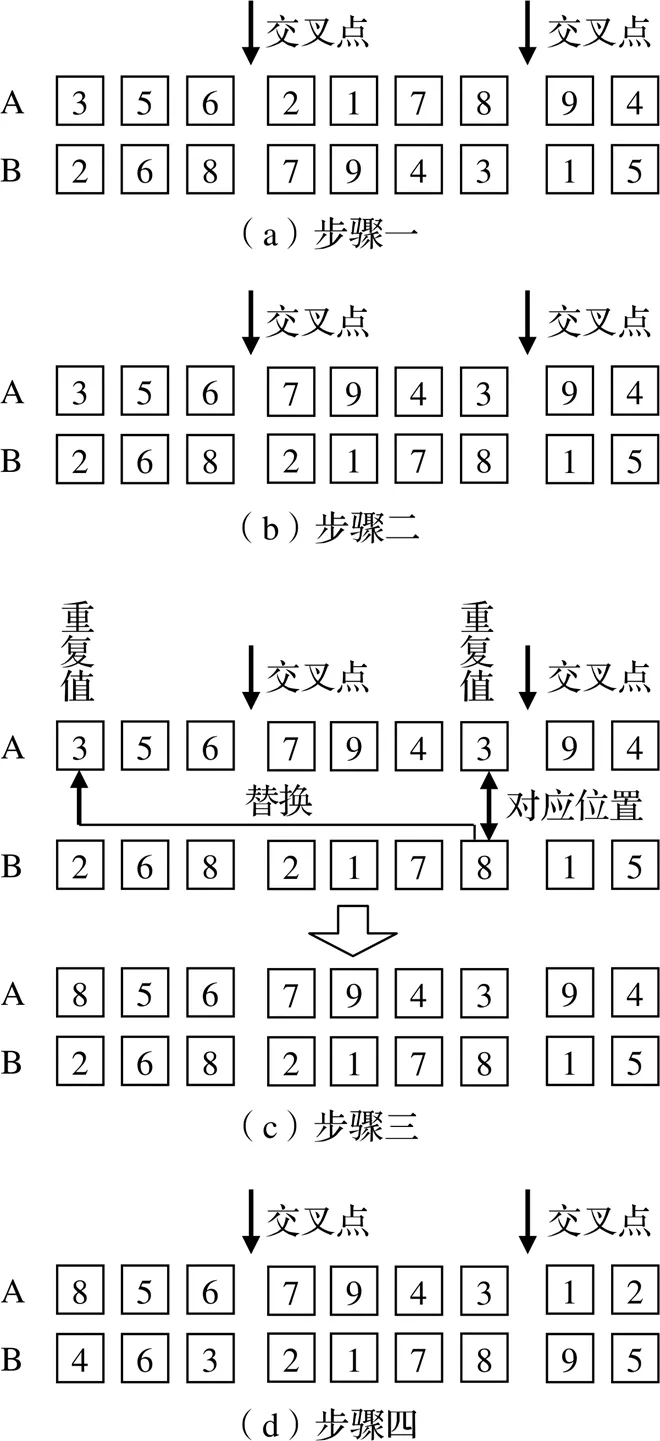
图5 交叉操作步骤
步骤一:随机选择父代A、B进行交叉变异,随机生成两个交叉点。
步骤二:对交叉点内的片段进行交叉操作。
步骤三:对于交叉后存在重复数值的子代,进行如下操作:将交叉点外的重复数值替换为交叉点内重复数值所对配对的交叉子代对应位置的值。
步骤四:重复步骤三直到没有重复数值为止,得到交叉子代A、B。
1.3.6 变异操作
随机选取个体中的两个数值进行位置交换。
2 实例分析
2.1 电子产品生产流程
以某电子产品生产车间为例,如图6所示,该车间生产线从投料开始,共经过七道工序,加工得到成品。
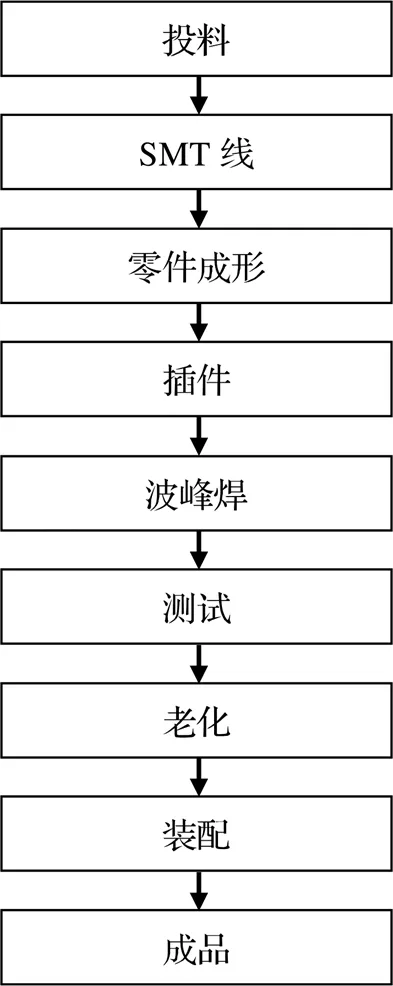
注:SMT为表面组装技术(Surface Mount Technology)。
2.2 订单信息
以该车间某条产线在2019年4月第2周的9个订单为例,每个订单需求包括产品型号、生产数量和订单交付期,如表1所示。其中型号B13、B17工艺流程无需插件工序,其余各型号产品生产均采用图6的工艺流程。
2.3 产品加工信息
已知测试与装配工序为早班、中班和晚班的三班制,工作时间依次为8:00~16:00、16:00~24:00、0:00~8:00,每日工作24 h;SMT线、零件成形、插件、波峰焊和老化工序为早班和中班的两班制,无晚班,每日工作16 h。每周工作5天。该产线各道工序的日有效生产能力如表2所示。9个订单共有9个产品型号,其生产信息如表3所示。
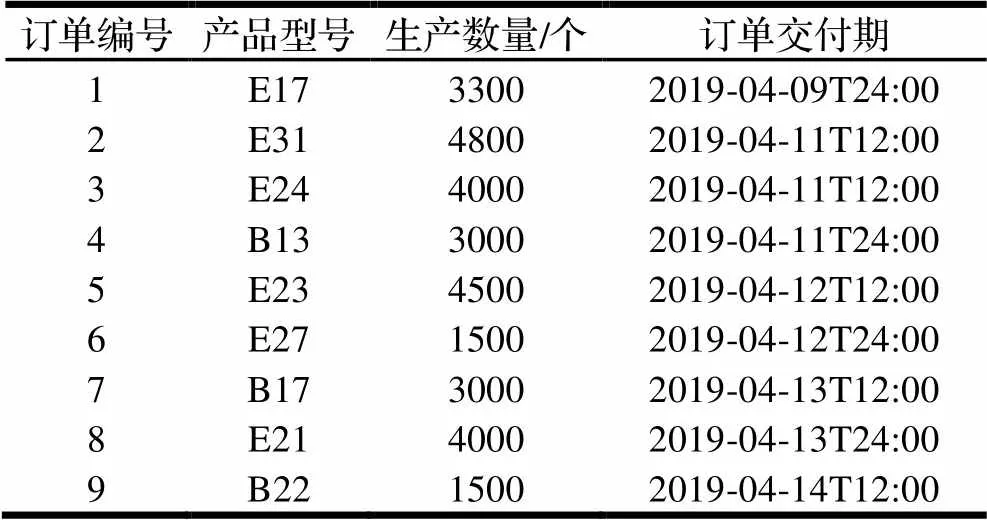
表1 订单信息
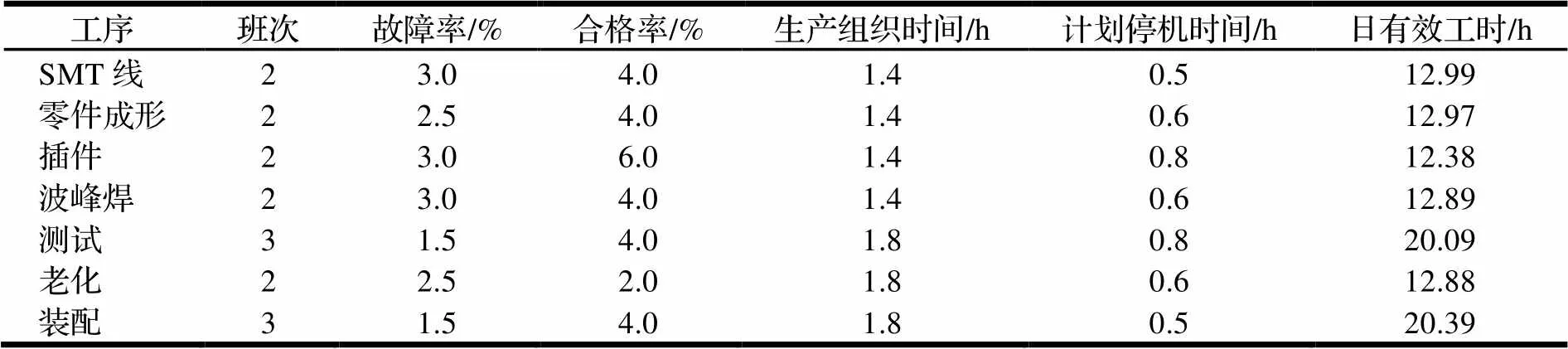
表2 各工作中心的日有效生产能力
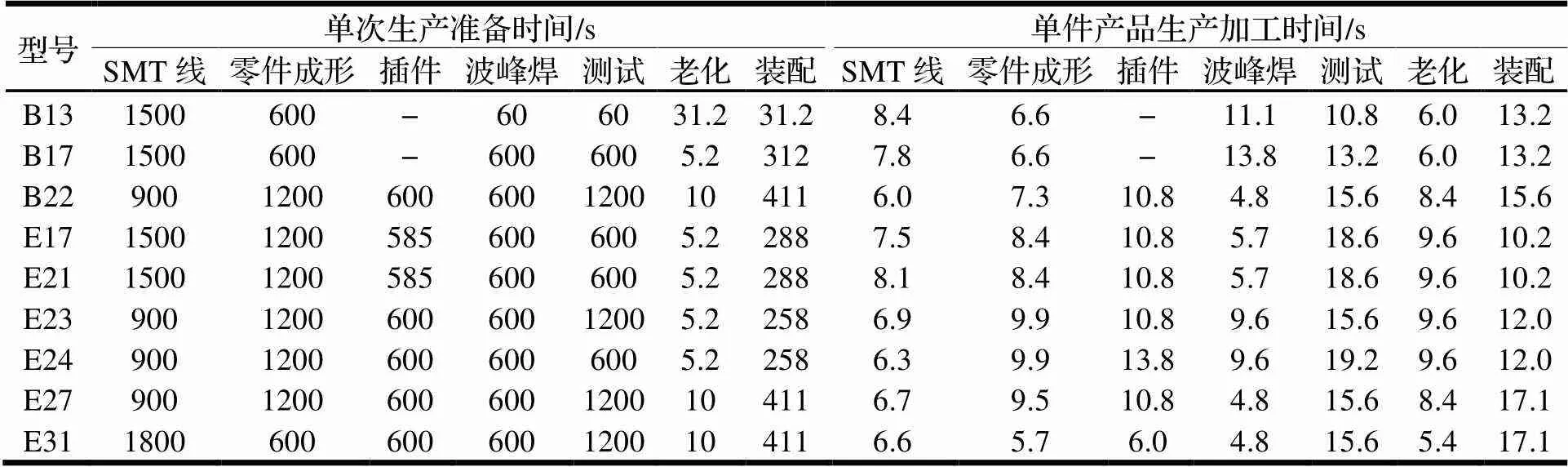
表3 各产品型号的生产信息
2.4 排程计算过程
(1)根据生产车间的产能受限资源识别模型,结合表1和表3数据分别计算计划期内各道工序的生产能力负荷率,结果如表4所示。得到波峰焊的生产能力负荷率最大,达到95%,判断测试工序为产能受限资源。
(2)由该车间的工艺流程和生产加工信息,使用Witness仿真软件建立该车间的离散系统仿真模型(模型略),采用从投料工序开始的推动式生产,机器故障率和生产合格率采用正态随机分布函数,生产批量设置为100,出货缓冲设置为理论生产时间的一半。依据订单需求计划,计算各个订单的生产缓冲大小。根据表4和式(2),计算各个订单的产能受限工序生产负荷大小,结果如表5所示。
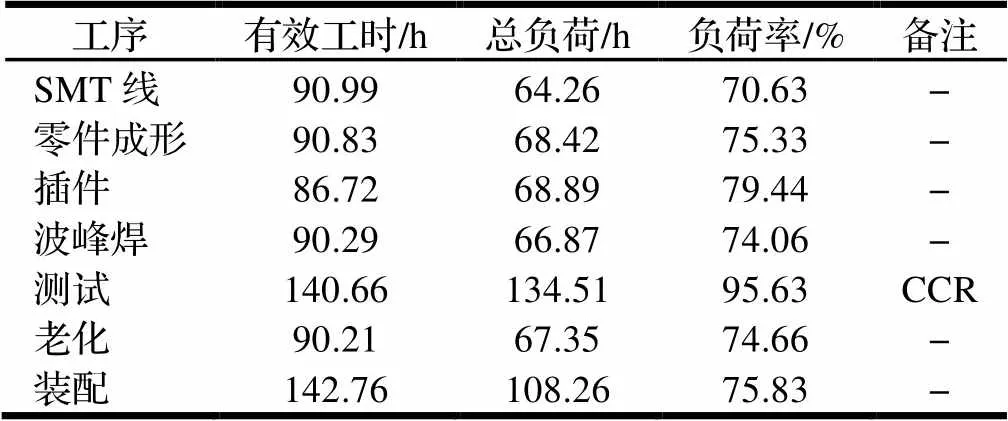
表4 各工序生产能力负荷率

表5 生产缓冲与产能受限资源生产负荷大小
(3)使用MATLAB编写该排程问题的遗传算法程序,初始种群数量设置为6个个体,依次进行适应度值计算、轮盘赌、交叉操作和变异操作。设置迭代终止条件为种群中出现准交率100%的个体,或迭代次数大于500次,输出计算结果。代入订单交期、生产缓冲、CCR负荷,计算得到排程结果如表6所示。
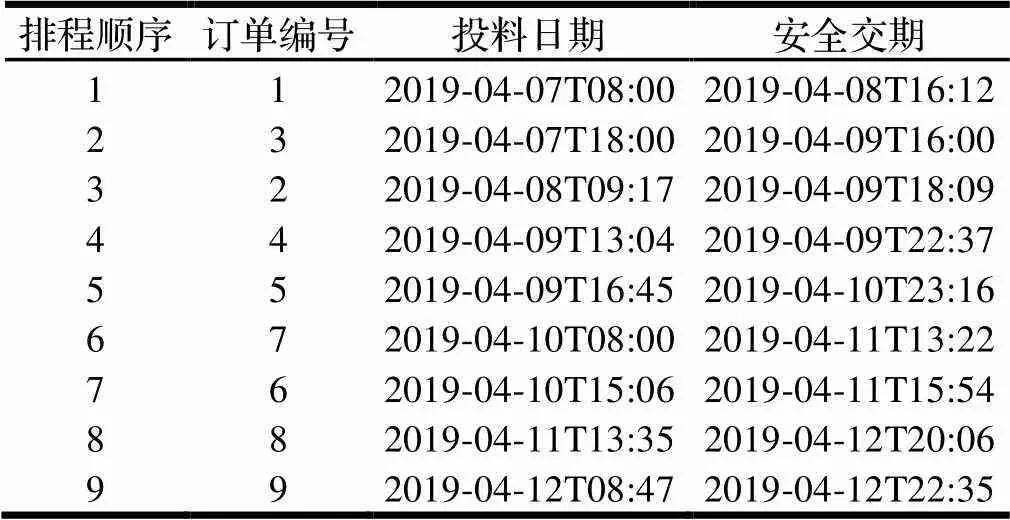
表6 排程结果
按照投料时间进行投料准备,根据投料工序的班次信息对投料时间进行调整以符合实际生产状况,对产能负荷资源进行监控和管理,结合仿真模型得到图7。
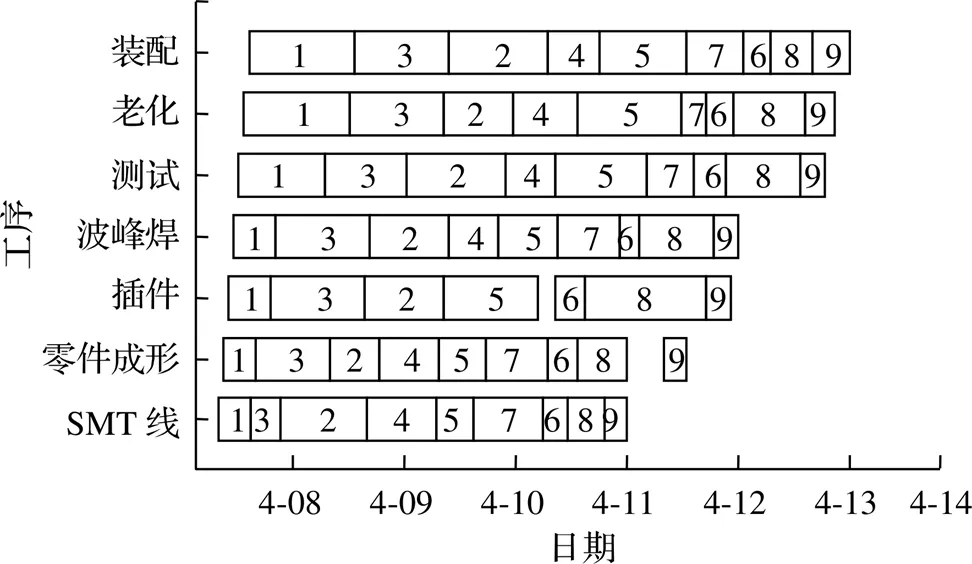
图7 生产排程甘特图
2.5 排程结果分析
由图7可知,在订单生产时间段产能受限资源的利用率达到了100%。对订单进行S-DBR排程后,产品的生产周期长和订单延迟交付风险等问题均得到改善,如表7所示。其中,传统排程是因为订单3的排程延误了交付时间。
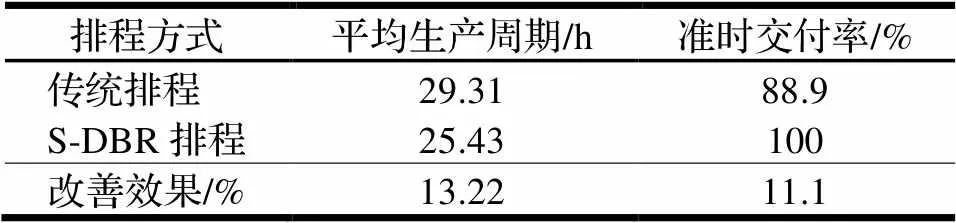
表7 S-DBR排程方案改善效果
3 结论
针对企业现有排程方案存在的生产周期长、订单准交率低的问题,提出了基于S-DBR理论的生产排程模型,并使用遗传算法进行求解。以某电子产品生产车间的生产数据为例,编制排程方案并验证排程模型的有效性。研究结果表明,使用该排程模型进行排程后,能够缩短订单生产周期并提高订单准交率。
[1] E. Schragenheim,H.W. Dettmer. Manufacturing at Warp Speed:Optimizing Supply Chain Business Performance[M]. Boca Raton:St. Lucie Press,2000.
[2]Yung-Chia Chang,Wen-Tso Huang. An enhanced model for SDBR in a randomreentrant flow shop environment[J]. International Journal of Production Research,2014(52):1808-1826.
[3]Jun-Huei Lee,Jia-Ging Chang,Chih-Hung Tsai c,et al. Research on enhancement of TOC Simplified Drum-Buffer-Rope system using novel generic procedures[J]. Expert Systems with Applications,2010(37):3747-3754.
[4]张义. 基于约束理论的多品种小批量生产计划与控制研究[D].大连:东北财经大学,2014.
[5]文帅. A型工厂环境S-DBR模型中瓶颈漂移问题的优化研究[D]. 大连:东北财经大学,2016.
[6]冷凯君,李芬,汪佩佩,等. 基于S-DBR方法的驾培排程研究[J]. 物流工程与管理,2020,42(7):159-167.
[7]李俚,夏晶,李露,等. 瓶颈工序影响下汽车电子生产车间排程研究[J]. 现代制造工程,2020(3):26-32.
[8]刘法逵. 强化S-DBR于紧急订单之应用[D]. 台湾:国立交通大学,2009.
[9]姜康,咸凯,郝宇. 基于订单拆分生产的MTO企业生产调度及算法研究[J]. 制造技术与机床,2018(3):143-148.
[10]郑秋雁,钱静. 基于DBR模型的生产排程研究[J]. 机械制造,2014,52(597):45-48.
[11]张顺堂,胡鹏. 面向敏捷生产的多品种小批量生产排程模型研究[J]. 现代制造技术与装备,2020(11):203-208.
[12]陈应飞,彭正超,胡晓兵,等. 基于改进模拟退火-遗传算法的FMS生产排程优化分析研究[J]. 机械,2021,48(2):7-16.
Research on Production Scheduling Based on S-DBR Model
LIU Wei,YUAN Hongbing
(School of Mechanical Engineering,Nanjing University of Science &Technology,Nanjing 210094,China)
The quality of production scheduling scheme has a great impact on the production efficiency of MTO enterprises. In order to shorten the average order processing time and improve the order delivery rate, relying on the Theory of Constraint (TOC) and the “Simple Drum-Buffer-Rope” (S-DBR) method, the internal bottleneck is identified by calculating the capacity load rate, and the order scheduling model based on S-DBR method is constructed to improve the order delivery rate. In this paper, a genetic algorithm for scheduling problem is designed, the individual coding, crossover and mutation of genetic algorithm are processed, and an electronic product production workshop is taken as the research object to find the solution. The results show that compared with traditional manual scheduling, this method can effectively shorten the production cycle and improve the order delivery rate.
TOC;S-DBR;production scheduling
TB491
A
10.3969/j.issn.1006-0316.2022.05.002
1006-0316 (2022) 05-0007-07
2021-10-09
刘威(1997-),男,湖南郴州人,硕士研究生,主要研究方向为企业信息化,E-mail:119101021631@njust.edu.cn;袁红兵 (1967-),男,江苏南通人,博士,副教授,主要研究方向为制造系统建模与仿真、计算机辅助设计与制造,E-mail:hbyuannj@126.com。

