一种基于三角面片法线方向设计复杂异形模型自由曲面分型面的方法
董香平,樊庆文,蒋汶莙,周明聪,熊良胤,裴宏亮*,
一种基于三角面片法线方向设计复杂异形模型自由曲面分型面的方法
董香平1,樊庆文1,蒋汶莙2,周明聪1,熊良胤1,裴宏亮*,1
(1.四川大学 机械工程学院,四川 成都 610065;2.中国工程物理研究院 总体工程研究所,四川 绵阳 621900)
提出一种基于复杂异形体模型三角面片法线方向设计异形分型面的方法,利用数字化三维模型构建三角面片模型的半边数据结构;计算所有三角面片法线方向,确定最佳拔模方向;根据三角面片法线方向与最佳拔模方向的空间关系,将各三角面片聚类并确定异形分型线,沿最佳拔模方向进行平移,得到复杂模型的异形分型模具。以人体胸骨模型的模具设计为例,计算人体胸骨模型的最佳拔模方向,设计异形分型线,获得胸骨模型的异形分型模具,并将该方法应用于人体其他器官模型。实验证明,该方法适应性强,能够快速确定异形分型面,具有重要的实用价值。
复杂异形模型;三角面片;分型线;最佳拔模方向
利用模具进行生产制造具有生产效率高和节省材料等优点。据统计,在21世纪的零部件制造中,75%的粗加工和50%的精加工都依靠模具完成[1]。在模具生产制造中,模具设计是关键。模具设计主要在于分型面的设计。常用的分型面有平面和曲面两类。对于结构和形状较简单的零件,设计者可依赖经验确定模具的拔模方向和分型面,但对于具有复杂形状特性的零件,其分型面通常都是自由曲面,仅凭经验和传统的设计方法无法获得最佳拔模方向和分型面[2-4]。
随着计算机图形学的发展,设计复杂异形体自由曲面分型面已经成为模具设计的热点和难点之一。自由曲面分型线的确定主要有三类典型方法:①Ravi等[5]提出通过拉伸零件最大投影轮廓线来确定模型的分型线;②Wong等[6]提出通过对塑件模型切片来生成分型线;③Nee等[7]提出通过对注塑件表面进行分组并抽取最大边环来自动生成分型线。这些方法一般只适用于一些规则产品的模具分型线确定,对于复杂外形结构产品,这些方法都较难起效。其中,通过人工经验确定模型的拔模方向,并借助计算机辅助设计软件来识别模型的设计特征以确定分型线的传统方法,仅适用于正向建模获得的形状简单的模型[8-10]。随着反求技术的发展,当前复杂模型大多通过逆向工程建立,其模型不包含模型设计或制造特征信息,借助现有软件对其进行异形分型面设计存在困难,获得正确的、满足开模要求的异形分型面设计是当前复杂模型模具设计的难点和热点之一[10-13]。
为了设计复杂异形体的自由曲面分型面,提出一种基于复杂异形体模型三角面片法线方向设计异形分型面的方法。将人体胸骨三维数字化实体模型转换为三角面片模型,构建三角面片模型的半边数据结构,计算所有三角面片法线方向,确定最佳拔模方向;根据三角面片法线方向与最佳拔模方向的空间关系,将各三角面片聚类,并确定异形分型线,完成复杂体的模具设计。该方法适应性强,能够快速确定异形分型面,具有重要的实用价值。
1 基于三角面片法线方向的分型面计算方法
1.1 基于半边数据结构的模型计算
逆向建模、CT扫描等建模手段获得的数据往往难以通过参数化CAD进行表示,一般采用逆向CAD建模技术来获得基本的几何单元,但在过程中会损失一定的精度和准确度。采用几何面片(三角面片)表示几何体,具有不降低采样准确度的优点,保持了采样最原始的精度。目前表示三角面片的数据多采用STL或者半边数据结构。
半边数据结构是指数据结构包含点、线和面的数据,同时将每个边的指代数据分为两个半边,每个半边都是一个有向边,两半边方向相反,如图1所示。
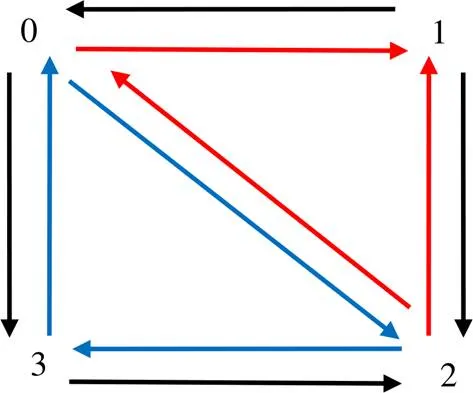
图1 半边数据结构示意图
如果一个边仅被一个面片占有(边界边),则这个面片仅拥有该边的其中一个半边,另一个半边为闲置状态。半边数据结构中顶点为包含出半边的指针或索引半边,半边为包含起始点、邻接面、下一条半边及上一条半边的指针或索引,面片为包含一条起始边的指针或索引。顶点的添加顺序决定了面片的起始半边,若向数据结构添加面片的操作为添加面(0,1,2),则有该面片的起始边为由0号指向1号的半边,可以用索引0→1表示该半边。同时,半边的邻接面是唯一的。若该半边有邻接面,则其下一条半边沿着邻接面的环路走;如果该半边没有邻接面(即为边界半边),则其下一条半边沿着边界走。
1.2 模型三角面片法线向量计算
对于以三角面片形式表示的模型,定义其流形三角面片集为,对集合中包含的所有三角形T的顶点集P求平均,获得:

利用单个三角面片的三个顶点求平均,获得三角面片的形心,根据三个顶点在直角坐标系中的坐标,计算三角面片的法线向量,结果如图2所示。

图2 三角面片法线向量计算原理图
对法线向量进行球面坐标系转换。球坐标系采用(,,)来表示一个点的位置,与在三维空间中位置的正交坐标系一一对应,其中,法线向量为标准向量(=1)。在球面坐标系中,坐标系原点与目标点之间的距离为,到的连线与直角坐标系+轴之间的夹角为顶角,到的连线在平面上的投影线与直角坐标系+轴之间的夹角为方位角,如图3所示。
根据直角坐标系和球面坐标系的转换关系,对直角坐标系中的任意一点(,,),其在球面坐标系中的位置可描述为:

1.3 三角面片法向量聚类计算
根据获得的球面坐标系,对顶角和方位角进行聚类分析。在二维空间中,存在一个点和与之相对应的圆,该圆以该点为圆心、以为半径,落在这个圆内的所有点和圆心矢量相减后得到一个向量,向量是以圆心为起点、落在圆内的点为终点。对这些向量进行求和,可以得到一个最终向量(Meanshift向量)M。有个样本点,=1, ...,,在空间中任选一点,则:

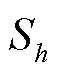

在基本的M向量中加入核函数,则M算法变形为:
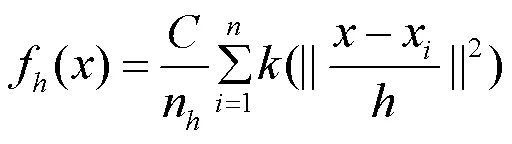
分别为全部聚类点数和在的圆区域的点数,二者比值为单位密度。
对式(5)求导,得:
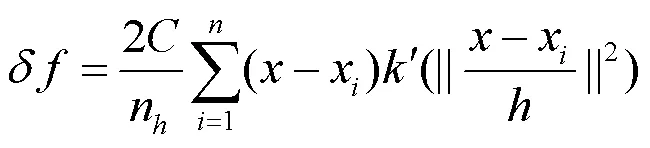
则有:
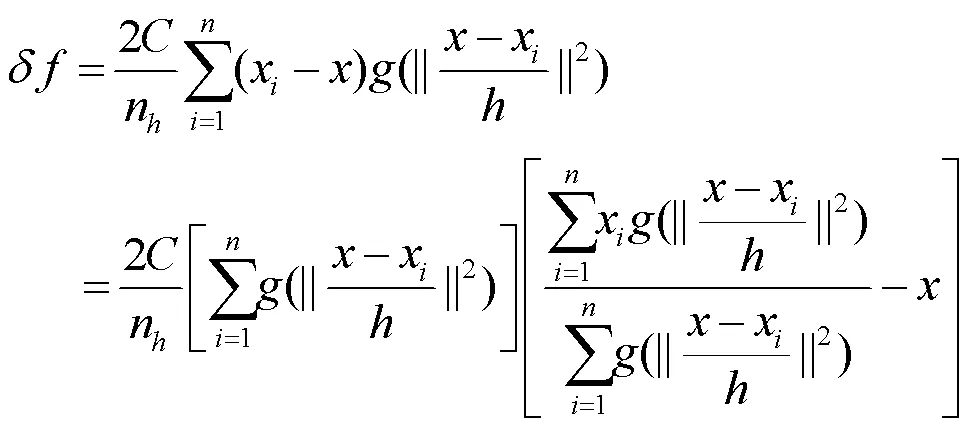
对式(7)取极值,得:
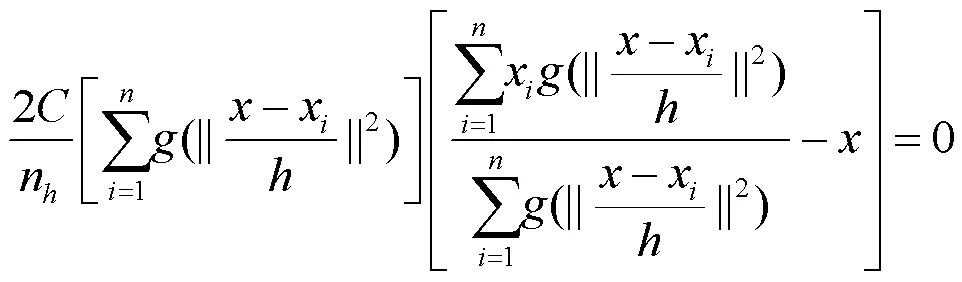
式(8)的第二项相当于一个M向量,即:

联立式(7)~(9),当且仅当M=0时,可以得出新的圆心坐标为:
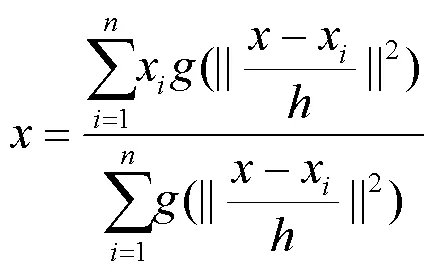
聚类计算所得到的点,作为聚类中心点,能够反映该数字模型中三角面片法线方向的主要方向。聚类中心点中的方位角和顶角与数字模型的所有三角面片的法线方向的偏离度最小,可以作为最佳拔模方向,减少拔模过程中模具与产品的干涉。
1.4 异形模具的自由曲面分型面计算
根据模型最佳拔模方向,计算复杂异形面三角面片法线方向与最佳拔模方向的点积运算。根据点积运算计算的正负对三角面片进行分类,划分为两个不同区域,为最佳拔模方向同向面和与最佳拔模方向反向面。根据同向面或反向面,得到边界线,即模型的分型线,如图4所示。根据异形分型线,沿拔模方向进行拉伸获得分型面,完成复杂异形体的模具设计。

图4 骨骼异形分型线
2 异形体模具的自由曲面分型面设计
分型面设计是模具设计中的关键步骤。分型面信息主要从复杂曲面中获取,包括主动脱模方向和分型面参数。主动脱模方向在于能够最大程度地避开模型中的凹面,以及防止在脱模过程中产生模具被卡等问题。分型面参数在于选择合理的分型切面,能够在主动脱模方向上生成最大截面,方便拔模。复杂异形曲面一般由激光扫描或者三维CT重建得到点云数据和三角面片数据,其数据表征不存在特征线、特征曲面等,难以通过特征线和特征曲面进行知识推理获得脱模方向和分型面参数。本文以胸骨模型为例,采用基于三角面片法线方向的分型面计算方法,进行异形体模具的自由曲面分型面设计,流程如图5所示。
辐射等效假人是用于代替人进行辐射实验的假人模型。以成都辐射等效假人(Chengdu Dosimetric Phantom,CDP)为基础,利用德国西门子对成都辐射等效假人全身扫描,获得502张CT数据集,其切片厚度为2 mm。将这些CT数据集导入Mimics软件中,重建获得胸骨三维模型。重建的胸骨三维模型以ASCII格式的STL文件存在,主要记录模型中三角面片的顶点位置和拓扑关系。读取胸骨模型STL文件,采用半边数据结构进行存储,并利用OpenGL对模型的边和面进行显示,结果如图6所示。

图5 复杂体异形分型面的设计原理

图6 半边数据结构下的胸骨模型
根据上述模型三角面片法线向量计算方法,遍历上述半边数据结构,计算在胸骨模型中三角面法线向量,获得胸骨模型法线向量集合,利用OpenGL对所有三角面片的法线向量进行绘制,如图7所示。
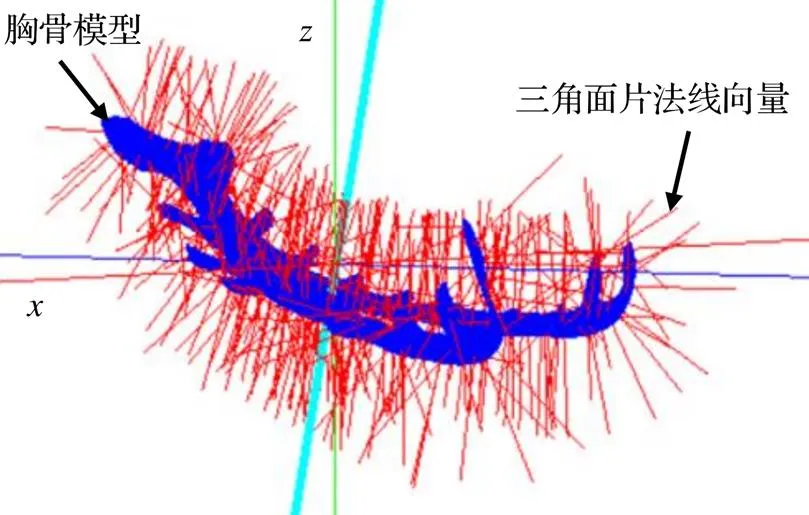
图7 胸骨模型三角面片法向量计算
在胸骨模型法线向量集合的基础上,对向量进行坐标系转换,可以计算得到三角形法线向量在球面坐标系中的分布,如图8(a)所示。胸骨模型法线向量集合主要集中在(0, 1.5)左右。为了得到最佳拔模方向,在球面坐标系中,对顶角和方位角进行聚类分析,设定聚类的类别为两类,即主方向类和其他类,结果如图8(b)所示。选择最大类为主方向类,作为胸骨模型拔模最佳方向,最佳拔模方向在球面坐标系下的绘制结果如图8(c)所示,箭头方向即为胸骨模型的最佳拔模方向。

图8 骨骼异形体拔模方向计算
根据胸骨模型最佳拔模方向,对所有三角面片的法线向量与最佳拔模方向进行点积运算,确定法线向量与最佳拔模方向的夹角。利用夹角的大小,判断三角面片法线向量是否与最佳拔模方向同向。对三角面片进行分类,划分为两个不同的区域,包括同向面和反向面。基于两区域的不同,可以遍历得到其边界线,作为模型的分型线。如图9所示。
最佳分型面可以将复杂异形体分成两个不同的曲面,沿最佳拔模方向对分型面进行平移作为模具的厚度,平移后和平移前的曲面即可构成一个实体,两个曲面分别平移后得到的实体,即模具实体,称为左模具和右模具,如图10所示。
同理,将算法应用到辐射等效假人的其他异形模具,包括大肠、胰腺、心脏、脾脏、肺部、肝脏六个人体器官和组织,计算得到其异形模具,如图11所示。
可以看出,不同异性复杂器官,其最佳拔模方向均与异形体形状相关,且均可能出现在多个方向。复杂异性体的分型面均为不规则空间曲线,难以通过特征曲线和特征曲面构建,较好地证明该算法具有良好的实用性和鲁棒性,能够针对不同异形体得到与之对应的模具。

图9 胸骨模型异形体分型线计算

图10 人体骨头异形模具计算
3 结论
提出一种基于三角面片法线方向确定最佳拔模方向、基于聚类分析计算异形分型线的复杂体模具设计方法,能够实现具有多自由曲面、复杂形状特征模型的快速、自动化分型线设计。以人体胸骨模型模具设计为例,提出一种基于复杂异形体模型三角面片法线方向设计异形分型面的方法。将人体胸骨三维数字化实体模型转换为三角面片模型,构建三角面片模型的半边数据结构,计算所有三角面片法线方向,确定最佳拔模方向;根据三角面片法线方向与最佳拔模方向的空间关系,将各三角面片聚类,并确定异形分型线,沿最佳拔模方向进行平移,即可完成复杂体的模具设计,得到复杂模型的异形分型模具。该方法适应性强,能够快速确定异形分型面,具有重要的实用价值。
[1]Rvai B,Srinivasna M N. Computer aided parting surface design[J]. Journal of Manufacturing System,1997(16):1-12.
[2]Wong T,Tan S T,Sze W S. Parting Line Formation by Slicing a 3D CAD Model[J]. Engineering with Computers,1998(14):330-343.
[3]谭晓波,艾勇,初光勇,等. 旋钮注塑模具设计与加工动态模拟[J]. 机械,2018,45(11):50-52.
[4]Nee A Y C,Fu M W,Fhu J Y H,et al. Automatic determination of 3-D parting lines and surfaces in plastic injection mold design[J]. Annals of CIRP,1998,47(l):95-98.
[5]Hui K C,Tan S T. Mould design with sweep operations a heuristic search approach[J]. Computer-Aided Design,1992(24):81-91.
[6]Hui,K. C. Geometric aspects of the mouldability of parts[J]. Computer Aided Design,1997(29):197-207.
[7]Subrahmanyam S R. A method for generation of machining and fixturing features from design features[J]. Computers in Industry,2002,47(3):269-287.
[8]李发致. 模具先进制造技术[M]. 北京:机械工业出版社,2003.
[9]石世铫. 注射模具设计与制造300问[J]. 汽车制造业,2011(9):58-58.
[10]ChenLinlin,Chou Shuoyan,Woo T C. Parting Direction of Mould and Die Design[J]. Computer-Aided Design,1993,25(12):762-768.
[11]Nee A Y C,Fu M W,Fhu J Y H,et al. Determination of Optimal Parting Directions inPlastic Injection Mold Design[J]. Annals of CIRP,1997,46(l):429-432.
[12] Nee A Y C,Fu M W,Fhu J Y H,et al. Automatic determination of 3-D parting lines and surfaces in plastic injection mold design[J]. Annals of CIRP,1998,47(l):95-98.
[13]Ying,Z.,Ding,H.,Xiong,Y. Virtual prototyping of mould design: geometric mouldability analysis for near-net-shape manufacturing parts by feature recognition and geometric reasoning[J]. Computer Aided Design,2001(33):137-154.
A Method of Designing Free-Form Parting Surface of Complex Special-Shaped Model Based on the Normal Direction of Triangular Patch
DONG Xiangping1,FAN Qingwen1,JIANG Wenjun2,ZHOU Mingcong1,XIONG Liangyin1,PEI Hongliang1
(1.School of Mechanical Engineering, Sichuan University, Chengdu 610065, China;2.Institute of System Engineering, China Academy of Engineering Physics, Mianyang 621900,China)
A method of designing a special-shaped parting surface based on the normal direction of the triangular patch of a complex special-shaped model is proposed. The digital three-dimensional model is used to construct the half-edge data structure of the triangular patch model. The normal direction of all the triangular faces is calculated and the best draft is determined. According to the spatial relationship between the normal direction of the triangular patch and the best draft direction, we clustered the triangular patches and determined the special-shaped parting line, and then translated along the best draft direction to obtain the special-shaped part of the complex model mold. Taking the mold design of the human sternum model as an example, we calculated the best draft direction of the human sternum model, designed the special-shaped fractal line, obtained the special-shaped fractal mold of the sternum model, and applied this method to other human organ models. Experiments have proved that the method has strong adaptability. It can quickly determine the special-shaped fractal surface, which is of important value in practice.
complex special-shaped model;triangular patch;parting line;optimum draft direction
TG76
A
10.3969/j.issn.1006-0316.2022.05.001
1006-0316 (2022) 05-0001-07
2021-11-17
四川省苗子工程项目(2020JDRC0029);四川省重点研发项目(22ZDYF2983)
董香平(1996-),男,四川广元人,硕士研究生,主要研究方向为计算几何、计算机视觉、模式识别,E-mail:522797562@qq.com。*
裴宏亮(1997-),男,甘肃岷县人,博士研究生,主要研究方向为计算机图形学、人工智能,E-mail:peihongliang@hotmail.com。

