基于模态分解-PSO-DNB深度学习的短期负荷预测研究

赵恩来，李向阳，王高峰，刘澎源，刘朝龙

(北京国网信通埃森哲信息技术有限公司，北京 100053)

随着分布式能源、储能、充电桩等新型供能方式持续大规模并网，促使配网智能化程度的不断发展和能效管理系统的智能化完善升级，将呈现出电力用户需求多样化的局面。电力负荷的预测结果将成为提升电网调度和配网智能化管控水平的重要依据[1]。因此，有必要对负荷预测的新方法、新技术开展研究，以此提高负荷预测的准确性。传统的负荷预测方法已无法满足负荷多元化的发展需求[2]。通常，负荷预测类型根据预测周期主要划分为(超)短期预测和中长期预测2大类。

本文重点以未来24 h内的负荷预测开展建模研究。文献[3]主要利用主成分分析原理提取数据样本集的特征量，采用如降维、简化数据空间等系列方法，有助于消除变量间的冗余性。文献[4]采用多层进化感知的深度训练模型，利用多层拓扑网络感知方法，将电力负荷数据向量由高维转化为低维，并从低维向量中提取出隐含特征量，以减小高维向量中的干扰成分。文献[5]详细探讨了基于一种ARIMA时间序列算法的光伏短期预测模型，该模型在阴雨天和晴天环境下均能获得较好的预测精度。文献[6]利用云计算相关技术设计了一种电力用户大数据分析平台，将智能电表、SCADA系统和各类传感器组合起来，将采集的数据整合并行优化预测电力用户短期数据，并结合预测数据开展边缘分析。深度学习理论作为当下人工智能领域的研究热点。另外，为提高短期负荷的预测精度，已有文献对短期负荷的预测算法进行了深入研究[7-9]，且从预测模型上也提高了日负荷(24 h内)的负荷精度[10-11]。深度信念网络(Deep Belief Network，DBN)预测模型可由多层受限玻尔兹曼机(Restricted Boltzmann Machine，RBM)组合而成，适用于求解维度高、复杂化的非线性问题。并对DBN训练模型开展研究发现，其模型的网络连接初始化权重系数是随机生成的，该方式极大促使DBN模型在训练中易陷入局部解，进而影响系统模型的预测效果。为此，本文利用自适应粒子群算法[12]优化模型的连接权重系数，建立自适应粒子群的DBN训练模型。此外，为了对负荷样本数据进行训前筛选，充分保证训练数据的合理性。本文充分利用了信号处理方法[13]—变分模态分解方法，可将样本负荷分解为一系列特征互异的子序列—模态量，并结合互信理论[14]利用其变化特点选用合理的输入量。

综上所述，为了跟随电力负荷周期性、随机性的变化特点，本文将原始负荷进行变分模态分解，并对各组模态集合建模分析，结合互信理论选择有效的输入，提出模态分解-PSO-DNB组合深度学习的短期负荷预测模型，对未来24 h内的负荷进行滚动预测，通过仿真结果说明了本文所给模型的有效性。

1 深度置信模型

深度学习模型作为多层神经训练网络的衍生模型[15]，其区别在于抽象化模型数据的低层特征，挖掘出数据内在的分布特征，利用训练较少的数据样本来获取数据的本质特征[16]。同时，深度学习模型很好地继承了神经网络训练模型的鲁棒特性，兼顾较少数据样本的条件下具备处理复杂函数的运算能力，本文将采用多隐层的非线性深度训练结构[17]。

1.1 深度学习单元

文献[18]对深度学习模型进行了深入分析，其核心内容是结合智能算法逐层训练每个多层受限玻尔兹曼机，最后结合反向传播算法对整个训练效果进行微调整。一般情况下，RBM模型包含有n个神经元、m个隐层神经元，其概率分布函数:

(1)

基于式(1)获得(v，h)的联合概率分布函数为:

(2)

(3)

式中，ai和bj分别为RBM模型可视层中的第i单元、隐含层第j单元的偏置量；vi和hj分别为对应的随机态；wij为权值系数；e-E(v，h|θ)为势函数；Z(θ)为配分量。

开展RBM模型训练主要为获取最优参数{wij，ai，bj}。为了克服数据采样效率低下的问题，文献[18]给出了一种散度对焦算法，适用于训练RBM模型。

1.2 深度学习模型

深度学习模型主要将RBM和自适应智能算法有机整合，如图1所示。其训练思路:①提取深度学习模型的底层数据特征量，用于模型设计顶层学习的输入变量，同时，采用由模型底层向高层逐层训练的模式；②训练至模型顶层后，再利用自适应粒子群算法对整个训练网络进行自适应优化调整，保证模型训练结果能跳出局部解。

图1 DBN训练流程Fig.1 DBN training process

鉴于DBN模型是由多个RBM模型整合而来，提高RBM的训练效率事关整个模型训练的核心地位。本文结合散度对焦算法进行快速训练，这有利于避开开展模型深度学习训练涉及的运算规模，直接采取RNM模型分散式训练，既提高训练速度，又能获得较优的初始训练参数。

RBM模型所需参数可利用学习训练的方式获取，并结合最大似然函数得到RBM参数的更新公式，具体表达式:

(4)

式中，λ为学习率；E()data为训练数据分布期望值；E()model为模型初始值设置的期望值。

为了减少取得无偏差值的运算量，结合CD梯度快速算法[19]对RBM参数予以优化，其更新公式:

(5)

式中，E()recon为模型数据重构后的期望值。

1.3 PSO算法

针对深度学习模型在训练中易陷入局部解的问题，本文利用PSO算法对模型网络的权重系数进行优化配置。传统的粒子群算法涉及的粒子速度和位置的更新公式[20]:

(6)

PSO算法的实施步骤参见文献[19]，本文设定模型的适应度函数:

(7)

式中，n、m分别为样本数和训练维数；pij、tij分别为训练数据的重构值和真实值。

2 短期预测模型

鉴于电力负荷非线性、随机性的分布规律，加之考虑到气候条件、外部经济和政治因素等外部环境，都会不同程度地反映在负荷波动特性上来。另外，季节因素、日期类型也会促进电力负荷发生波动。尽管如此，电力负荷依然带有很强的周期性。为充分反映电力负荷的波动变化，本文运用模态分解法[13]对负荷序列进行特征化处理，获取区分性辨识的效果，以此提升学习模型的预测精度。同时，变量输入的合理选取也决定了预测负荷的准确性，为避免过度地依赖人工经验，本文充分考虑输入和输出变量间的关联信息，并筛选出对预测结果较大影响的输入变量集合。

2.1 数据分析

(1)数据异常分析。利用离群数据判定原则[21]，设定w的异常数据判据:

(8)

式中，Q1、Q3分别对应第一、第三四分位数；IQR为四分位距。

(2)数据分布分析。为了确定样本负荷数据的时间分布，对采集的样本数据图形化，可大致确定高峰负荷的时间节点。以某市电网供应负荷2020年1月—8月实测负荷开展数据分析，采样间隔为1 h，结合文献[13]所述方法对样本数据进行分解，模态分解的部分结果如图2所示。

图2 负荷原始序列及模态分解结果 Fig.2 Load original sequence and modal decomposition results

由图2所知，U1的振幅均值最小，有较大波动，规律性较差；U2、U3具有较好的规律性和周期性；U4、U5振幅均值较大，波动平缓，规律性较好。

基于上述分析，若对U1—U5分别建模，致使训练模型的效率降低且运算任务加重。本文利用近似熵方法[22]，先对近似熵值相近的状态序列采取合并处理，从而利于随机分量、细节分量和趋势分量集合获取。

由图3可知，结合近似熵方法处理后，随机分量的平均周期和振幅分别约为5.34 h和21.34 MW，该分量的意义主要体现工作和休息期间电力用户的用电规律，且具有较大波动性。细节分量的平均周期和振幅分别约为11.88 h和125.15 MW，该分量主要反映了各类用户生产的用电规律，规律性较好。趋势分量的平均周期和振幅分别约为24 h和342.15 MW，该分量重点反映以天为单位的负荷变化情况，规律性较好，周期性稳定。

图3 模态重构结果Fig.3 Modal reconstruction results

2.2 数据处理

深度学习模型主要用于训练输入样本数据，并通过植入优化的权重系数w和偏置量b，以获取较高质量的输入数据，故在训练前应对样本数据进行质化处理。

(1)默认值处理。考虑到电力负荷的测量数据具备连续性特点，在正常运行状态下数据不存在短时跃变，故选取t-1时刻的负荷代替t时刻的默认值。

(2)数据异常处理。筛选出异常数据，并将此部分数据(如电压、电流等电气量)同配网运行正常变化范围内的监测数据校核，从而剔除异常数据。

(3)归一化处理。对于训练模型而言，选择的输入变量需对影响因子和输出变量间的关联性综合考虑，为避免因物理量纲不统一引起的换算问题，需对数据采取归一化处理，具体方式为:

(9)

2.3 变量输入

本文结合互信理论[14]输入有效的变量。作为信息论中熵的概念，互信理论用来表征多变量信息的共享规模。随机离散变量x、y间交互信息量化为:

(10)

式中，n、m分别为随机离散变量x、y的样本数。若二者随机量之间的交互信息越多，表明变量间的关联性越强；反之，关联性越弱。本文重点研究短期(24 h内)负荷预测，则输入变量应着重考虑历史日负荷、典型温度等变量。结合负荷周期性和交互理论，对样本数据进行分类处理。

2.4 特征化处理

数据特征化处理是将样本数据转化为模型数据，其目的为模型获取更好的数据特征，提高机器学习效率。

(1)特征信息提取。提取出原始数据的隐藏信息，挖掘数据内涵特征。结合电力负荷特点，综合考虑月、周、小时、工作日以及峰谷等属性，结合向量编码原则对样本数据的特征信息进行编码组合。

(2)特征信息融合。该过程主要将数据源和应用场景按照对应原则相互融合，并根据电力网络参数的相应物理意义，本文选用电力网络中的有功和无功、电压和电流等数据参与特征融合，其架构如图4所示。

图4 特征工程整合流程 Fig.4 Feature engineering integration process

2.5 评价指标

采用平均绝对百分比误差和均方根误差作为模型预测效果评价指标，计算公式为:

(11)

2.6 模型训练流程

综合以上论述，本文将获得的电力运行样本数据开展短时负荷预测模型建模。模态分解-PSO-DNB深度进化模型如图5所示。

图5 模态分解-PSO-DNB深度进化模型Fig.5 Modal decomposition-PSO-DNB deep evolution model

3 算例分析

本文选择某地区实际负荷数据进行相关验证，采集的样本数据为某地区10 kV配电网络系统2020年1月—8月的运行负荷数据，采样周期为1 h。其中，样本数据含储能、分布式发电和充电桩等负荷类型，分布式发电以光伏发电为主，供电负荷类型主要为楼宇负荷，该类型负荷的峰谷时段明显，且季节性波动范围较大。为了验证深度学习特征提取预测模型的准确性，结合多场景开展深度学习仿真训练。

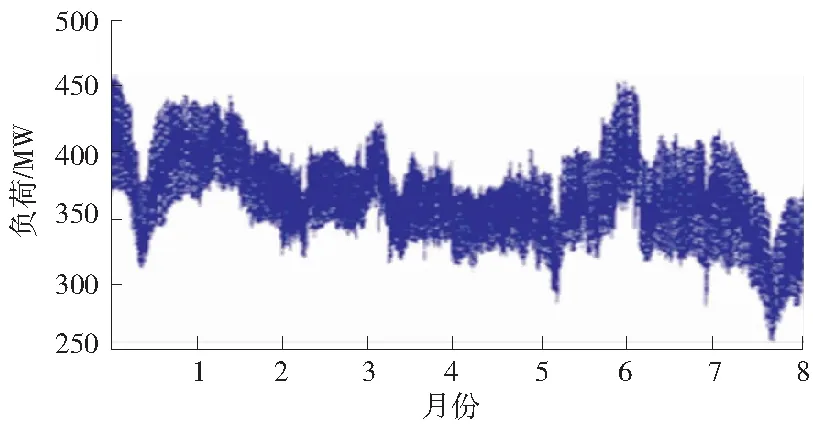
图6 原始样本数据Fig.6 Original sample data

设定2020年1月1日—2020年6月30日期间的数据作为训练样本，剩余数据作为测试样本。通过仿真，可得出模态分解-PSO-DNB深度进化模型的中间性能见表1。

表1 模态分解-PSO-DNB深度进化模型的预测性能Tab.1 Predictive performance of modal decomposition-PSO-DBN deep evolution model

由表1可知，当模型的隐含层数递增时，δMAPE、δRMSE总体上呈先递减后递增的趋势，而模型训练所需时间随着节点数呈递增变化。综合表2测试结果，本文构建的模态分解-PSO-DBN模型选择隐含层数为3，节点数选择64。模型其余参数设置见文献[23]。模型训练的迭代次数设为1 000次，学习率设为10-3。

通过仿真优化后，本文获得的预测结果见表2。由表2可知，通过不同模型训练结果发现，基于进化深度学习模型训练得到的负荷结果具有更好的拟合精度，能够跟随负荷曲线进行自适应调整。

表2 部分节点负荷预测值Tab.2 Partial node load forecast

4 结论

本文利用模态分解-PSO-DBN模型对电力负荷数据进行相应训练，可作用于电力短期负荷的预测下研究。得出的结论如下。

(1)利用模态分解方法将原始负荷进行序列分解，提取其特征分量。促进清晰掌握用电行为的周期特性。

(2)综合考虑样本负荷的历史规律、温度及日期类型等因素，结合互信息理论整合各输入分量，避免了人工经验干预的缺陷。

(3)通过循环滚动24 h负荷预测场景，采用自适应PSO算法优化深度学习模型的权重参数，提高了模型的预测性能。

参考文献(References):

[1] 康重庆，夏清，张伯明.电力系统负荷预测研究综述与发展方向的探讨[J].电力系统自动化，2004，28(17):1-11.

Kang Chongqing，Xia Qing，Zhang Boming.Review of power system load forecasting and its development[J].Automation of Electric Power Systems，2004，28(17):1-11.

[2] 陈艳平，毛弋，陈萍，等.基于EEMD-样本熵和 Elman神经网络的短期电力负荷预测[J].电力系统及其自动化学报，2016，28(3): 59-64.

Chen Yanping，Mao Yi，Chen Ping，et al.Short-term power load forecasting based on EEMD-sample entropy and Elman neural network[J].Proceedings of the CSU-EPSA，2016，28(3): 59-64.

[3] Amjady N，Keynia F.A new prediction strategy for price spike forecasting of day-ahead electricity markets[J].Ap-plied Soft Computing，2011，11(6):4246-4256.

[4] Gensler A，Henze J，Sick B，et al.Deep learning for solar power forecasting - an approach using Auto Encoder and LSTM neural networks[C]//IEEE International Conference on Systems，Man，and Cybernetics.Budapest，Hungary，2016:2858-2865.

[5] 赵滨滨，王莹，王彬，等.基于ARIMA时间序列的分布式光伏系统输出功率预测方法研究[J].可再生能源，2019，37(6):820-823.

Zhao Binbin，Wang Ying，Wang Bin，et al.Photovoltaic power prediction in distribution network based on ARIMA model time series[J].Renewable Energy Resources，2019，37(6):820-823.

[6] 王德文，孙志伟.电力用户侧大数据分析与并行负荷预测[J].中国电机工程学报，2015，35(3):527-537.

Wang Dewen，Sun Zhiwei.Big data analysis and parallel load forecasting of electric power user side[J].Proceedings of the CSEE，2015，35(3):527-537.

[7] 葛少云，贾鸥莎，刘洪.基于遗传灰色神经网络模型的实时电价条件下短期电力负荷预测[J].电网技术，2012，36(1):224-229.

Ge Shaoyun，Jia Ousha，Liu Hong.A gray neural network model improved by genetic algorithm for short-term load forecasting in price-sensitive environment[J].Power System Technology，2012，36(1):224-229.

[8] 王保义，王冬阳，张少敏.基于Spark和IPPSO-LSSVM 的短期分布式电力负荷预测算法[J].电力自动化设备，2016，36(1): 117-122.

Wang Baoyi，Wang Dongyang，Zhang Shaomin.Distributed short-term load forecasting algorithm based on Spark and IPPSO-LSSVM[J].Electric Power Automation Equipment，2016，36(1):117-122.

[9] 曾鸣，吕春泉，田廓，等.基于细菌群落趋药性优化的最小二乘支持向量机短期负荷预测方法[J].中国电机工程学报，2011，31(34):93-99.

Zeng Ming，Lü Chunquan，Tian Kuo，et al.Least squares-support vector machine load forecasting approach optimized by bacterial colony chemotaxis method[J].Proceedings of the CSEE，2011，31(34):93-99.

[10] 孙谦，姚建刚，赵俊，等.基于最优交集相似日选取的短期母线负荷综合预测[J].中国电机工程学报，2013，33(4):126-134.

Sun Qian，Yao Jiangang，Zhao Jun，et al.Short-term bus load integrated forecasting based on selecting optimal intersection similar days[J].Proceedings of the CSEE，2013，33(4):126-134.

[11] Ceperic E，Ceperic V，Baric A.A strategy for short-term load forecasting by support vector regression machines[J].IEEE Transactions on Power Systems，2013，28(4):4356-4364.

[12] 朱经纬，方虎生，邵发明，等.自适应粒子群算法求冗余机械臂逆运动学解[J].计算机工程与应用，2019，55(14):215-220.

Zhu Jingwei，Fang Husheng，Shao Faming，et al.Self-adaptive particle swarm optimization algorithm for solving inverse kinematics problem of redundant manipulator[J].Computer Engineering and Applications，2019，55(14):215-220.

[13] 张晓宇，张建成，王宁，等.基于变分模态分解的混合储能系统协调控制[J].中国电力，2018，51(9):169-177.

Zhang Xiaoyu，Zhang Jiancheng，Wang Ning，et al.Coordinated control of hybrid energy storage system based on variational mode decomposition[J].Electric Power，2018，51(9): 165-173.

[14] Vahabie A H，Yousefi M M R，Araabi B N，et al.Mutual information based input selection in neuro-fuzzy modeling for short term load forecasting of Iran National Power System[C]//2007 IEEE International Conference on Control and Automation.Guangzhou，China:IEEE，2007:2710-2715.

[15] Yuan Lecun，Bengio Y，Hinton G.Deep learning[J].Nature，2015，521(7553):436-444.

[16] 孙志军，薛磊，许阳明，等.深度学习研究综述[J].计算机应用研究，2012，29(8):2806-2810.

Sun Zhijun，Xue Lei，Xu Yangming，et al.Overview of deep learning[J].Application Research of Computers，2012，29(8):2806-2810.

[17] Bengio Y.Deep learning of representations for unsuper-vised and transfer learning[J].Workshop on Unsupervised & Transfer Learning，2012，7:1-20.

[18] Sauer D U，Wenzl H.Comparison of different approaches for lifetime prediction of electrochemical systems-using lead-acid batteries as example[J].Journal of Power Sources，2008，176(2):534-546.

[19] 孙莉敏，张聪.线性反问题的一个改进CD算法[J].数学的实践与认识，2020，50(5):184-189.

Sun Limin，Zhang Cong.An Improved CD algorithm for linear inverse problems[J].Journal of Mathematics in Practice and Theory，2020，50(5):184-189.

[20] 付雪松，王建林，胡志雄，等.基于动态权重PSO算法的眼科OCT设备横向分辨率检测[J].仪器仪表学报，2019，40(9):145-153.

Fu Xuesong，Wang Jianlin，Hu Zhixiong，et al.Lateral resolution detection of ophthalmic OCT equipment based on dynamic weight PSO algorithm[J].Chinese Journal of Scientific Instrument，2019，40(9):145-153.

[21] 孙毅，李世豪，崔灿，等.基于高斯核函数改进的电力用户用电数据离群点检测方法[J].电网技术，2018，42(5):1595-1604.

Sun Yi，Li Shihao，Cui Can，et al.Improved outlier detection method of power consumer data based on Gaussian kernel function[J].Power System Technology，2018，42(5):1595-1604.

[22] 李勋贵，魏宁，魏霞.系统复杂性测度参数确定的新方法及其应用[J].系统工程理论与实践，2018，38(1):252-262.

Li Xungui，Wei Ning，Wei Xia.A new method for determining parameters of system complexity measures and its application.Systems Engineering-Theory & Practice，2018，38(1): 252-262.

[23] 向育鹏，卫志农，孙国强，等.基于全寿命周期成本的配电网蓄电池储能系统的优化配置[J].电网技术，2015(1):264-270.

Xiang Yupeng，Wei Zhinong，Sun Guoqiang，et al.Life cycle cost based optimal configuration of battery energy storage system in distribution network[J].Power System Technology，2015(1):264-270.