一类定点与动形之间的最值问题

在2021 年中考试题中，有一类以正方形为载体，探究定点与动态图形之间的最值问题.

例1 （2021·陕西）如图1，正方形ABCD的 边 长 为4，⊙O的 半 径 为1. 若⊙O在正方形ABCD内平移（⊙O可以与该正方形的边相切），则点A到⊙O上的点的距离的最大值为______.

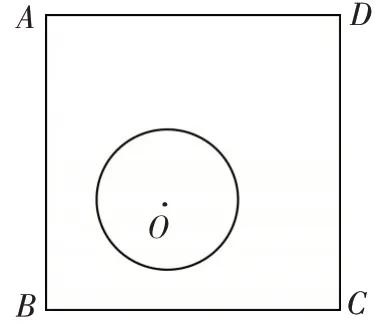
图1

分析：当点在圆外时，该点到圆的最大和最小距离的定义为：圆外点和圆心所连线段与圆的交点是最近点，圆外点和最近点的距离就是最小值；圆外点和圆心所连线段的延长线与圆的交点是最远点，圆外点和最远点的距离就是最大值.要求得点A到⊙O上点的距离的最大值，需要定位⊙O平移后的位置“信息”，⊙O需向着与点A距离最远的方向平移.不难想象，点O应沿着对角线AC 的方向平移，达到⊙O分别与边BC,DC相切的位置“状态”，如图2，⊙O的这一平移“终止”位置，正是问题需要的位置.

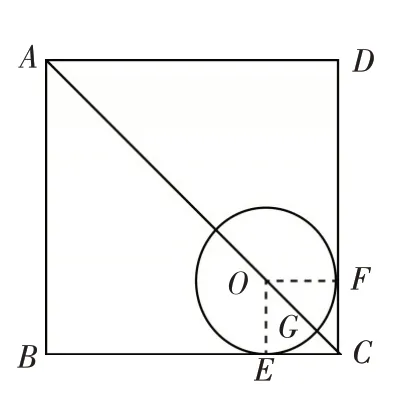
图2

解：当点O沿着对角线AC方向平移，使⊙O分别与边BC,DC相切于点E,F时，AC与⊙O的交点G即为点A到⊙O的最远点，如图2. 连接OE,OF，则四边形OECF为正方形，OE=OF=1，由勾股定理得OC= 2 .在Rt△ABC中，由 勾 股 定 理 得AC=4 2 ，∴AO=AC-OC= 3 2 . 又OG=1 ，∴AG=AO+OG= 3 2 +1，即点A到⊙O上的点的距离的最大值为3 2 +1.

感悟：观察是思维的先导.此题的最值的获取是借助了我们的观察、联想和猜想，而这种猜想又是合乎情理，合乎事实的.平时的数学教学，我们惯以计算和推理两个指标来衡量学生数学能力的高低.而从这道题的解析中，首先要想象和猜想出⊙O的“终止”位置，才会有之后的计算和推理.所以学习数学，应借助知识这一载体，养成学生勤于观察、善于联想的思维习惯，而后再引导学生去证明和计算.

举一反三：若题中的条件不变，是否存在点A到⊙O的距离的最小值呢？若存在，求出这个最小值.

例2（2021·上海）定义：平面上一点到图形最短距离为d，如图3，OP=2 ，正 方 形ABCD边 长 为2，O为正方形中心，当正方形ABCD绕O旋转时，则d 的取值范围为_____.

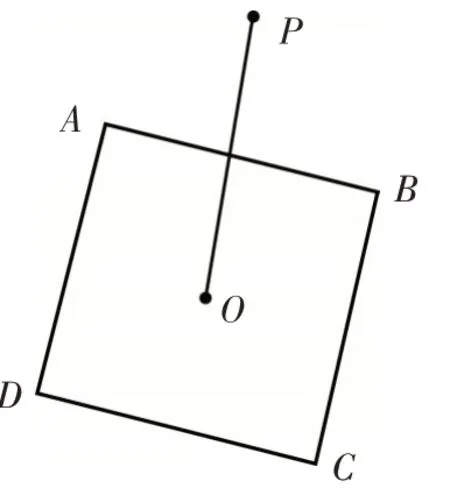
图3

分析：点P,O的位置都是固定的，正方形ABCD绕O旋转，位置是动态的，所以点P 到正方形的最短距离将随正方形位置的变化而变化. 正方形ABCD绕其中心O旋转，但点A,B,C,D均在以点O为圆心，为半径的圆上.观察OP与正方形顶点和边的特殊位置关系是问题解答的突破口.解：由勾股定理得点O到点A,B,C,D的距离均为. 虽正方形ABCD绕其中心O旋转，但点A,B,C,D均在以点O为圆心，为半径的圆上（旋转）.当P,B,O三点共线时，此时PB的长就是点P到⊙O的最近距离，也是点P到正方形ABCD的最短距离，如图4 所示，此时PB=PO-OB=2-，即d=2-；当OP⊥AB于E时，有OE=1，点P到AB的距离即为点P到正方形ABCD的最小距离，如图5 所示，此时PE=OP-OE=2-1=1，即d=1.综上两种情形，得点P到正方形ABCD距离d的取值范围为：2-≤d≤1.

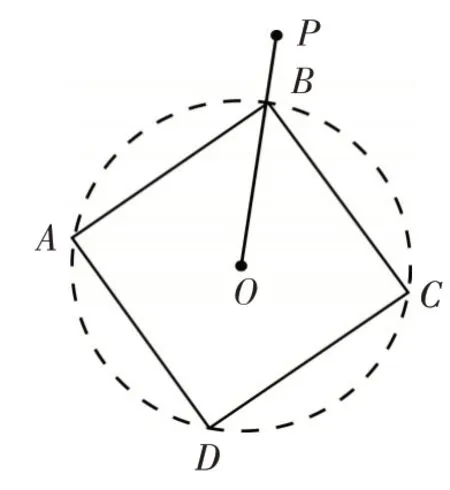
图4

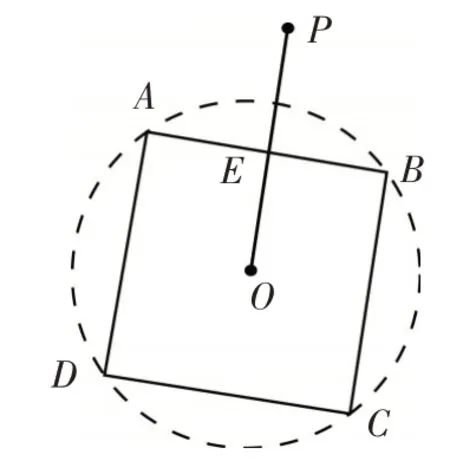
图5

感悟：正方形的旋转，使我们难以把握点P到正方形距离的最小值，不妨我们先从特殊的位置关系入手，如OP过正方形的某一顶点，OP与正方形的一条边垂直，再借助观察、联想、推理和计算来解答.

动中求静，是捕捉问题质的重要原则.而这一过程，离不开我们的观察、联想和猜想，有了这些东西的支撑，或许我们就有所发现、有所创新，可以说这些东西是学习中更有含金量的东西.