基于双流网络的步态特征表述算法
杜晓雨,张学东
(辽宁科技大学 计算机与软件工程学院,辽宁 鞍山 114051)
近年来,生物特征识别技术已经在个人身份认证领域取得很多成果[1]。指纹、人脸识别技术较为成熟,但在远距离、遮挡等复杂场景下识别效果不够理想[2-4]。步态识别以其难伪装、无需人为配合、远距离采集的优势,成为国内外研究热点。人体步态识别方法可分为模型方法和非模型方法[5]。模型方法是将人体运动时的关节角度、人体重心等进行建模,提取其生物特征。Cunada等[6]通过傅里叶级数描述手臂的运动,应用时间数据收集技术提取模型。Scaramuzza等[7]利用多个摄像头采集人体行走时的步态图像,将其进行三维重建,进而分析运动状态。模型方法提取到的特征较为准确,但需要建模才能实现,运算量大,处理速度较慢。非模型方法也称基于外观的步态识别方法,主要采集人在行走时的动态信息,并利用数学方法表示步态特征。这种方法根据外部轮廓计算步态能量图(Gait engery image,GEI)[8],将图像轮廓对齐,在时间上进行叠加取平均值,得到的图像作为步态特征,还衍生了运动能量图和帧间差能量图[9-12]。非模型方法不需要建模,能表示运动过程中的动静信息,同时对视角的变化也具有一定的稳定性[13]。本文针对步态帧图像数据量大、网络处理速度慢的问题,提出以步态序列集合为基础的特征表述算法。该算法属于非模型方法,通过对步态序列集合进行边缘检测,再经过主成分分析法进行降维操作,在保证识别率的同时降低算法的复杂度,从而节省网络处理时间。
1 步态特征表述
1.1 步态序列集合
网络对二值图像进行特征提取过程中,分析的仅仅是轮廓边缘信息,大面积的前景像素使用率较低。为了提高运算效率,首先对步态帧图像进行高斯滤波处理,有效去除图像中的高频噪声。再利用Soble算子计算图像梯度的幅值M和方向θ
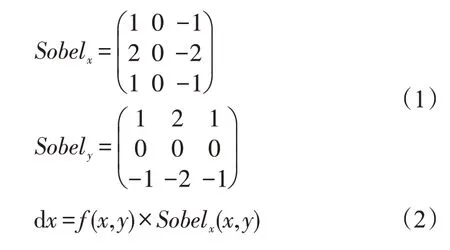

式中:Sobelx(x,y)和Sob ely(x,y)分别为Sobel水平和垂直算子;f为输入图像;dx和dy分别为水平和垂直方向的差分量。
根据梯度方向角对梯度幅值进行非极大值抑制,使其由多像素宽图像变为单像素宽图像。最后使用双阈值筛选算法连接边缘,去除孤立噪声点,得到步态轮廓图(Gait contour image,GCI),如图1所示。

图1 步态轮廓图Fig.1 Gait profile image
步态特征既包含人体结构特征,还包含人在行走过程中随时间变化的行为特征。因此,通过构造步态序列图可以表达人在行走时的时序信息。首先将一个步态周期的步态轮廓图进行堆叠,再沿其m轴作nl平面的投影,得到一个步态周期的步态序列图。生成步态序列图的过程如图2所示。

图2 步态序列图Fig.2 Gait sequence diagram
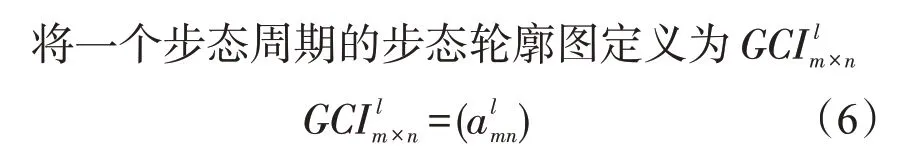
式中:m和n为步态轮廓图的坐标,m=0,1,…,M-1,n=0,1,…,N-1;l为帧索引,l=0,1,…,L-1;M为轮廓图的高度;N为轮廓图的宽度;L为步态序列的总帧数。

式中:a、b为步态序列叠加得到的像素体积;n=0,1,…,X-1;l=0,1,…,Y-1;m=0,1,…,Z-1;X为步态序列图的宽度;Z为序列图的高度;Y为生成的样本总数。
由算法生成的步态序列图与轮廓图的大小一致,若对应的时序长度不足,则使用重采样的方法对时序长度进行补齐。因此,一个序列步态轮廓图如图3所示。一个序列步态序列图如图4所示。

图3 一个序列的步态轮廓图Fig.3 Gait contours of a sequence

图4 一个序列的步态序列图Fig.4 Gait sequence diagrams of a sequence
1.2 主成分分析法
主成分分析法(Principal component analysis,PCA)是一种常见的数据分析算法,常用于高维数据的降维,提取数据的主要特征分量,最先应用于人脸识别等方面。本文将此算法运用于步态识别领域,解决步态识别过程中数据信息量大、计算困难的问题。PCA算法将步态特征维度高的图像矩阵转变为低维特征矩阵,有效压缩图像的数据信息。
PCA算法将n维特征映射到d维上,d维特征是经过正交变换的主成分特征,是对原始空间进行重新构造。空间重构的方法是令数据在重构方向的投影方差值最大,数据在重构空间的分布分散,更易于区分。


式中:λ是矩阵S的特征值;u1是矩阵S的特征向量;u^1是方差优化函数。
主成分分析选取前d个最大的特征值对应的特征向量,组成新的特征空间,这些新变量是两两不相关的。经过边缘检测处理的步态特征图尺寸为64×64,将图片的每一列看作一个特征,则需要对64个维度的特征空间进行主成分分析降维。主成分维度d值选取方法:对N张步态特征图样本集进行降维,其协方差矩阵的维度为64×64,将矩阵特征分解后将特征值排序:λ1≥λ2≥…≥λm。t为重构阈值,设t=0.99。按照特征值降序排列,选取d个特征值,使
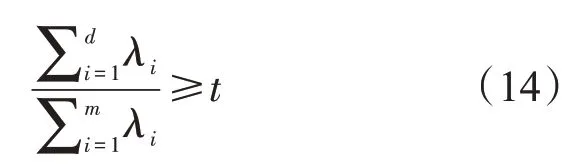
成立,取最小d值,重构的特征空间主成分贡献率为原特征空间的0.99以上。
主成分贡献率曲线如图5所示。取24作为最终降维后的主成分维度,主成分贡献率为0.99,64×64的特征矩阵通过PCA降维后得到64×24的特征矩阵,样本信息密度增加,能够简化后续的步态特征提取。
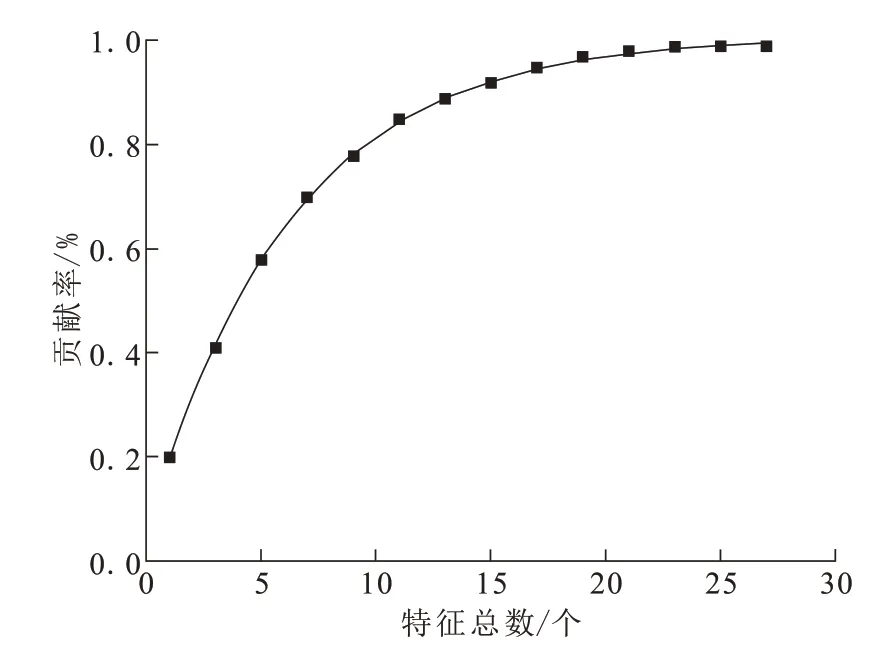
图5 主成分贡献率Fig.5 Contribution rates of principal components
1.3 双流网络模型
传统双流网络的空间域和时间域主干网络为8层,包括5层卷积层和3层全连接层。空间域网络的输入为视频中随机抽取的单帧图像,时空域网络的输入为几个相邻帧之间叠加的光流图像。为了进一步提升模型的特征提取能力和网络的泛化能力,本文采用残差网络ResNet替换传统双流网络的8层网络结构,两个分支子网络分别进行特征提取。网络结构如图6所示。分支子网络参数如表1所示。
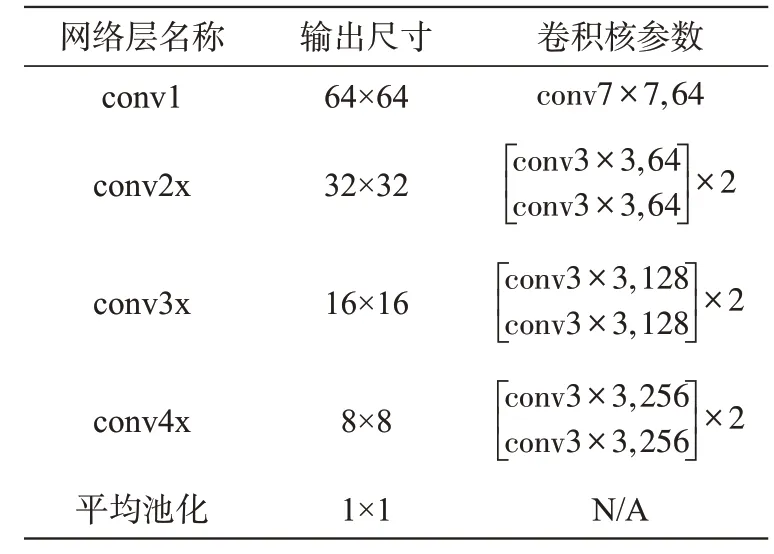
表1 分支子网络参数Tab.1 Trunk network parameters
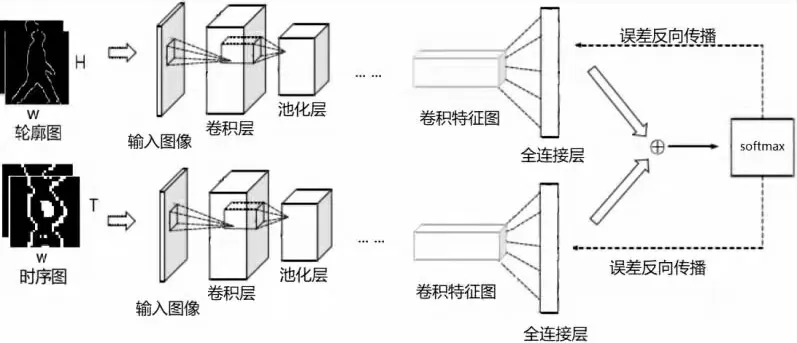
图6 双流网络结构示意图Fig.6 Schematic diagrams of dual flow network
ResNet共有5种深度的网络结构,本文利用ResNet18作为双流卷积网络的主干网络,通过设置多个残差块,解决训练过程中产生的梯度消失问题。网络的输入数据是尺寸为64×64的步态特征图,特征图经过一层卷积层、三组残差块进行特征提取,再经过平均池化和全连接层得到特征序列,最终利用softmax函数计算概率分数。
2 仿真实验
2.1 训练与测试策略
双流网络模型使用CASIA-B数据集[14]。首先将64×64的步态帧图像经过边缘检测得到步态轮廓图后生成步态序列图,再对步态轮廓图和步态序列图进行主成分分析,降维得到步态特征图,将其作为步态特征送入网络。利用双流网络进行特征融合并使用输出层进行分类,通过损失函数得到的误差,判断模型对数据的拟合程度。最后利用反向传播优化参数,直到模型趋于稳定。使用训练中生成的网络模型对测试样本进行特征提取分类并识别,并统计实验结果。
2.2 仿真实验及结果分析
目前对于步态识别的研究主要以步态能量图作为输入数据[15],而本文的算法以步态序列作为输入数据。采用双流网络对比这两种输入数据的步态识别效果。
将数据集处理为步态能量图和步态序列集合两种形式,分别将步态能量图与步态集合作为输入数据,再利用双流网络进行训练测试。将数据集中的数据分为相同数量的两份,每份数据都包含62个行人的步态数据信息。一份用于模型的训练,一份用于模型性能的评估。将步态数据处理为一个周期的轮廓图和序列图,经过双流网络进行训练测试。再将步态数据处理成步态能量图,经过网络进行训练测试。
数据集包括三种步态:正常行走、背包行走和穿大衣行走,如图7所示。仿真实验结果如表2所示。三种行走条件下,以步态序列集合作为网络输入的准确率均高于步态能量图。在正常行走条件下,步态序列集合比步态能量图的精确率高7.93%。协变量因素对步态序列的干扰较小,因此,在穿大衣和背包的行走条件下准确率也优于步态能量图。

图7 步态数据集Fig.7 Gait dataset

表2 仿真实验结果Tab.2 Comparison of GEI and gait collection experiments
为了测试边缘检测及主成分分析降维的效果,对比数据处理前后单帧图像和完整步态周期像素点的总数。单帧图像在数据降维的过程中,数据量的变化幅度较小,降维前共有4 096个像素点,降维后像素点达到1 536个。但一个完整周期的像素总数在降维前后发生巨大变化,降维前共有98 364个像素点,降维后像素点仅有36 864个。数据量的减少使得样本信息密度增加,但数据降维操作会舍弃部分特征向量,会对特征判别有一定的影响。
利用三种双流卷积神经网络对降维前后的数据进行仿真实验,步态识别的准确率结果如表3所示。在三种行走条件下,本文提出的双流网络+边缘检测+PCA步态识别算法准确率都稍低于双流网络以及双流网络+边缘检测算法,但运行时间缩短0.59 s,运算效率提高17.3%。因为在PCA主成分降维过程中,丢弃的贡献率低的数据也带有一定的步态特征信息,从而影响步态识别准确率。

表3 双流网络下实验结果对比Tab.3 Comparison of experimental results under dual flow network
3 结论
步态识别是通过摄像头捕捉人的行走姿态,依靠算法分析进行身份鉴定的一种远距离身份识别技术。本文提出基于边缘检测的步态序列集合通过主成分分析降维处理的特征表述算法。首先对步态图像进行边缘检测得到步态轮廓图,通过构造生成步态时序图,再对步态轮廓图和步态序列图进行主成分分析降维,得到步态特征图,将其作为步态特征输入网络,进行分类识别。在CASIA-B数据集上进行仿真实验表明,边缘检测和主成分分析法降维在保证识别率的同时,能够提高网络的计算效率。

