Matrix‐based method for solving decision domains of neighbourhood multigranulation decision‐theoretic rough sets

Jiajun Chen|Shuhao Yu|Wenjie Wei|Yan Ma

1College of Electronics and Information Engineering,West Anhui University,Lu'an,China

2College of Electronics and Information Engineering,Tongji University,Shanghai,China

AbstractIt is more and more important to analyse and process complex data for gaining more valuable knowledge and making more accurate decisions.The multigranulation decision theory based on conditional probability and cost loss has the advantage of processing decision-making problems from multi-levels and multi-angles,and the neighbourhood rough set model (NRS) can facilitate the analysis and processing of numerical or mixed type data,and can address the limitation of multigranulation decision-theoretic rough sets(MG-DTRS),which is not easy to cope with complex data.Based on the in-depth study of hybrid-valued decision systems and MG-DTRS models,this study analysed neighbourhood MG-DTRS (NMG-DTRS) deeply by fusing MG-DTRS and NRS;a matrixbased approach for approximation sets of NMG-DTRS model was proposed on the basis of the matrix representations of concepts;the positive,boundary and negative domains were constructed from the matrix perspective,and the concept of positive decision recognition rate was introduced.Furthermore,the authors explored the related properties of NMG-DTRS model,and designed and described the corresponding solving algorithms in detail.Finally,some experimental results that were employed not only verified the effectiveness and feasibility of the proposed algorithm,but also showed the relationship between the decision recognition rate and the granularity and threshold.

KEYWORDS decision domains,decision making,NMG-DTRS,rough set theory

1|INTRODUCTION

Rough set theory [1,2] is an important theory in the field of artificial intelligence.It is a new mathematical tool to cope with uncertain and imprecise data,which was proposed by Pawlak in 1982,and has extensive applications in various fields,such as government decision-making,financial analysis,data mining and medical system.Decision-theoretic rough sets model (DTRS)[3,4] is an important decision-making model based on probability and risk-cost sensitivity for solving practical decision problems with uncertain data,and multigranulation decision theory is devoted to analyse target decision objects from multilevels and multi-angles [5-8].DTRS and a large number of extended models have been studied to address the corresponding requirements in recent years [9-13].However,most proposed analysis methods in the light of the classical rough set theory can only be used to process single type of data,such as symbolicdata,andthere aresome limitationsin the processing of complex data such as numerical or hybrid-valued type decision systems [14].Furthermore,with the increasing application of data science and artificial intelligence technology,data from all walks of life are becoming more huge,complex,diverse and uncertain,and people need more comprehensive and diversified analysis and processing of these complex data in order to obtain more valuable knowledge and make more accurate decisions,so the research of multi-granulation decision making methods for numerical data and mixed data has been paid more and more attention.Qian et al.[15]first developed the MG-DTRS model by the combination of multigranulation rough sets and the Bayesian decision theory,however,the application scope of the models in the light of the equivalence relation was limited because it was not easy to cope with all kinds of complex data,especially hybrid-valued type information systems with numerical type and categorical type properties.In order to address the limitation,Lin et al.put forward the neighbourhood rough set models(NRS)in literature[16,17],in the following years,several types of generalised NRS models were widely used in various domains.Literature [18] discussed DTRS model in the neighbourhood system environment,literature [14] deeply analysed the neighbourhood DTRS(NDTRS)and MG-DTRS model,and proposed an incomplete neighbourhood multigranulation decision-theoretic rough set (NMG-DTRS) model;reference[19] investigated neighbourhood multigranulation rough sets(NMRS) and the attribute reduction method for incomplete information systems with symbolic type and numerical type properties.In addition to the mentioned frameworks,some important insights based on these models have been explored,such as the application of matrix technology.In rough set theory,matrix has the advantages of intuitive and simple knowledge representation and reasoning,so,matrix-based methods have been widely used in some fields of rough set[20-28],including decision making information systems [22,28],covering approximate spaces [26-28],neighbourhood information systems [20,23,25] and multigranulation spaces [23,25,28].Literature [23] discussed the matrix-based approaches for dynamic updating approximations in multigranulation rough sets,literature[20]and literature[25]studied,respectively,the problems of decisiondomains updating andapproximationsupdating in neighbourhood multigranulation space by introducing the matrix technique into the neighbourhood multigranulation rough set,and the description of maximum and minimum covering rough sets was discussed in detail based on matrix technology in literature [26].Among the above achievements,there were few research works on NMG-DTRS in the complex information system,although literature[22]illustrated the matrix approach for decision-theoretic rough sets,it is not suitable for neighbourhood information systems in multi-granularity environment.Literature [14] explored two types of NMGDTRS in detail based on the incomplete hybrid -valued decision system,however,the knowledge representation based on the models are difficult to understand and has some computational complexity.In this study,in view of the characteristics of matrix in rough set context,we introduced the matrix technique into NMG-DTRS and proposed a matrix-based method for solving decision domains of the NMG-DTRS model for hybridvalued decision information systems,the positive,boundary and negative domains were constructed from the matrix perspective.Furthermore,we explored the related properties of the NMG-DTRS model,and the corresponding solving algorithms based on the proposed method were designed and described in detail.

The other sections of the paper were organised as follows.First,the fundamental knowledge of DTRS,MG-DTRS and NMG-DTRS was reviewed briefly in Section 2,in Section 3,a novel matrix-based method for approximation sets of the NMG-DTRS model was proposed on the basis of the matrix representations of a series of concepts,and the positive,boundary and negative domains were constructed based on the NMG-DTRS model.Furthermore,the related properties of the NMG-DTRS model and implementation algorithms were discussed in depth.Finally,some experimental results were employed to prove the algorithm is feasible and effective.

2|PRELIMINARY KNOWLEDGE

Here,we reviewed some related works of DTRS,MG-DTRS and neighbourhood MG-DTRS models in this section.

2.1|DTRS

IS=（U，A=C ∪D，V，f）is a given decision table information system,where U represents the target space object set,C and D (C ∩D=∅）are the condition attributes and decision attributes,respectively,indicates a non-empty value set of c ∈A,and the mapping function f is expressed by f :U ×A →V.For any given non-empty subset P ⊆C,an objectxcan been represented by its equivalence relationswe can obtain the lower approximation sets and the upper approximation sets of X'on the subset P byIn the light of the aboveare called the positive domains,boundary domains and negative domains of X'about the subset P,respectively.

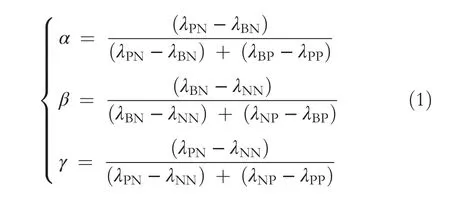
Prorder POS（α，β）（X）,BND（α，β）（X）and NEG（α，β）（X）indicate positive domains,boundary domains and negative domains of X based on thresholds（α，β）.In view of the Bayesian decision procedure,letλPP,λBPandλNPrepresent the loss functions of classifying objectxinto domains POS（α，β）（X）,BND（α，β）（X）and NEG（α，β）（X）,respectively,when objectxbelongs to category X;λPN，λBNandλNNrepresent the loss functions that it be classified in domains POS（α，β）（X）,BND（α，β）（X）and NEG（α，β）（X）when objectxis not in category X,respectively.Consider the reasonable assumption that the losses of taking the right action is less than or equal to the losses of taking the wrong action,namely,we can knowλPP≤λBP＜λNPandλNN≤λBN＜λPN,the thresholds（α，β）can be obtained from all loss functions by Equation (1).The detailed derivation process is shown in reference [4],where 1 ≥α＞β≥0.

Based on the Bayesian decision procedure,for∀X'⊆U，P ⊆C,the decision rules closely related to the probability of objectxbased on thresholds（α，β）in the DTRS model can been obtained:

（1）if probabilityPr（X′｜[x]P）≥αis satisfied，then

objectx∈POS（α，β）（X′）

（2）if probabilityβ≤Pr（X′｜[x]P）＜αis satisfied，then

objectx∈BND（α，β）（X′）

（3）if probabilityPr（X′｜[x]P）＜βis satisfied，then

objectx∈NEG（α，β）（X′）

For the given decision information system IS=（U，A=C ∪D，V，f）,supposeπD=｛D1，D2，…，Dm｝ indicates the partitions on the target space U with respect to the decision attribute D ∈A,for any attribute subsetB⊆Cand ∀x ∈U,then we can get the probabilistic lower and upper approximations ofπDabout B in the DTRS model as follows:

2.2|MG‐DTRS

MG-DTRS is a rough decision theory in the context of multigranulation,which combines the DTRS theory and the multigranulation idea,can been widely used in many fields,including multi-source data analysis,distributive information systems and intelligent decision making from data with multi dimensions.In this section,the pessimistic MG-DTRS model and the optimistic one were discussed as two focusses in multigranulation rough sets.The relevant definitions were described as follows.

Definition 1Suppose IS=（U，A=C ∪D，V，f）be a decision table information system,where the universeU=｛xi｜,A1，A2，…Am⊆Aare m granular structures,[xi]Akdenotes equivalence granule ofxiabout thekth granular structureAk（k=1，2，…，m）.For anyX′⊆U,then the approximations ofX′in the optimistic MGDTRS model are expressed by the following:

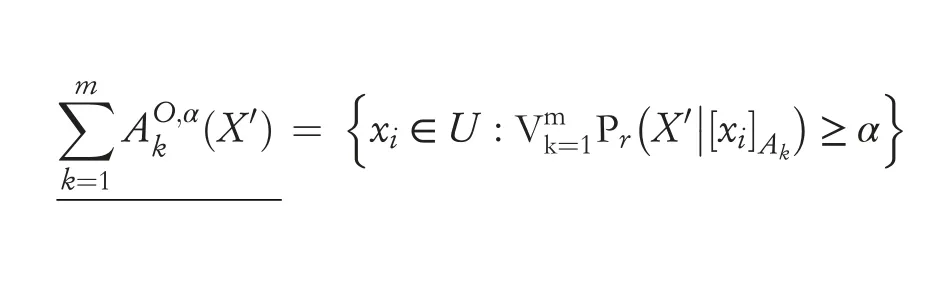
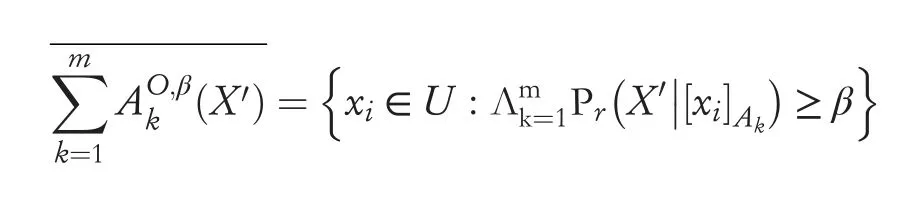
where ∧and ∨denote the logic conjunction (AND) and the logic disjunction(OR) operations,respectively.

Definition 2Suppose IS=（U，A=C ∪D，V，f）be a decision table information system,where the universeU=｛xi｜,A1，A2，…Am⊆Aare m granular structures,[xi]Akdenotes equivalence granule ofxiabout thekth granular structureAk（k=1，2，…，m）.For anyX′⊆U,then the approximations ofX′in the pessimistic MG-DTRS model are expressed by the following:

where ∧and ∨denote the logic conjunction(AND) and the logic disjunction(OR) operations,respectively.

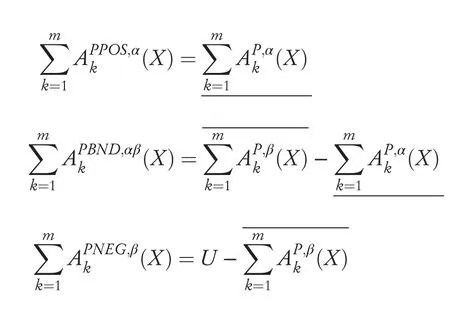
ByDefinition 1,Definition 2and the decision rules in the decision-theoretic rough set model,the positive domains,boundary domains and negative domains of the optimistic MG-DTRS model can be,respectively,formalised as follows:

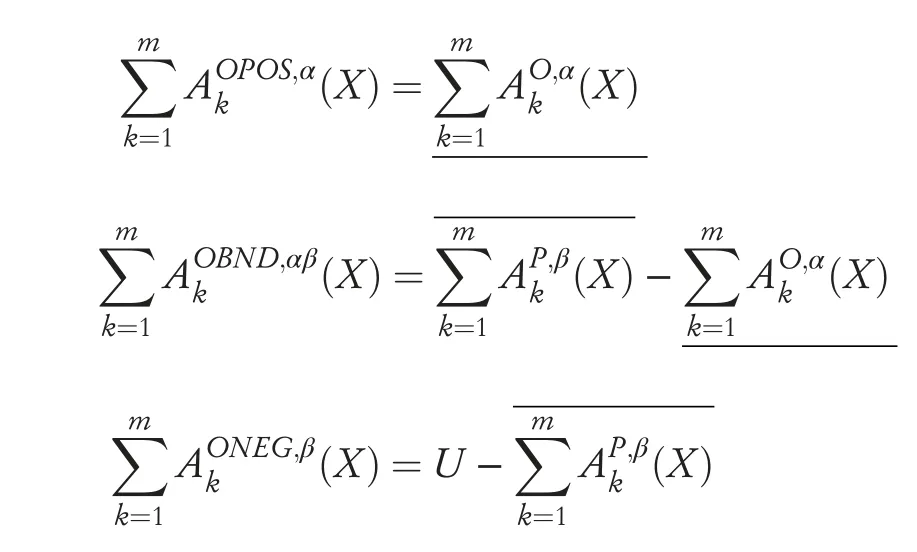
The positive domains,boundary domains and negative domains of the pessimistic MG-DTRS model can be,respectively,formalised as follows:

2.3|NMG‐DTRS

MG-DTRS models are based on classical DTRS,which uses equivalence relations to partition the target object universe and generate multiple equivalence classes as basic concepts [21].However,the models based on the equivalence relation are not easy to cope with all kinds of complex data,especially hybridvalued type information system with numerical type and categorical type properties[14,20].Therefore,the neighbourhood rough set(NRS) was put forward because of the advantage of facilitating the analysis and processing of numerical or mixed type data.The NRS model uses neighbourhood relation to partition the decision object target spaces and replaces the equivalence classes with neighbourhood particles.In NMGDTRS models,the equivalence classes based on conditional probability of classical MG-DTRS are replaced by the neighbourhood granularity,the details are as follows.

A given neighbourhood information system NIS=（U，A=C ∪D，V，f）,where U represents the target space objects,C and D(C ∩D=∅）are the condition attributes and decision attributes,respectively,suppose any B ⊆C be a condition attribute subset,for any objectxi∈U,then the neighbourhood granularityNB（xi）of the objectxibased on the attribute subset B is defined byis the neighbourhood radius.Δ is a distance function,here only the Euclidean distance is taken as a metric function and is defined as follows:

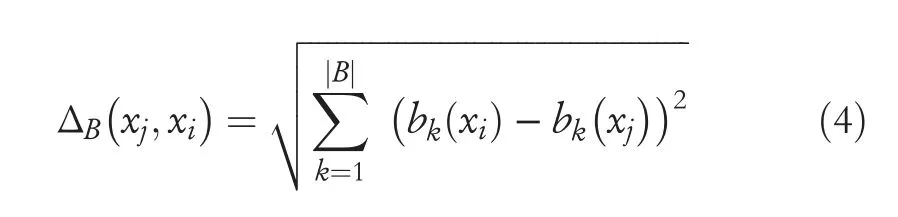
According to Definition 1 and 2,we can obtain the approximations in the NMG-DTRS model by substituting neighbourhood granularity for conditional equivalence classes.

Definition 3Suppose NIS=（U，A=C ∪D，V，f）be a neighbourhood decision table information system,where U represents the target space objects,U=｛xi｜i=1，2，…，n｝ andA1，A2，…Am⊆Aare m granular structures,NAk（xi）denotes neighbourhood granularity of the objectxiabout granular structureAk,where（k=1，2，…，m）.Giventhe thresholds（α，β）,for∀X⊆U,then the approximation sets ofXbased on the optimistic NMG-DTRS model are defined by the following:

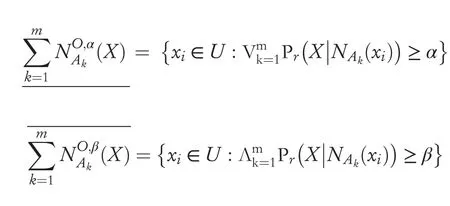
Definition 4Suppose NIS=（U，A=C ∪D，V，f）be a neighbourhood decision table information system,where U represents the target space objects,U=｛xi｜i=1，2，…，n｝ andA1，A2，…Am⊆Aare m granular structures,NAk（xi）denotes neighbourhood granularity of the objectxiabout granular structureAk,where（k=1，2，…，m）.Given the thresholds（α，β）,for ∀X⊆U,then the approximation sets ofXbased on the pessimistic NMG-DTRS model are defined by the following:

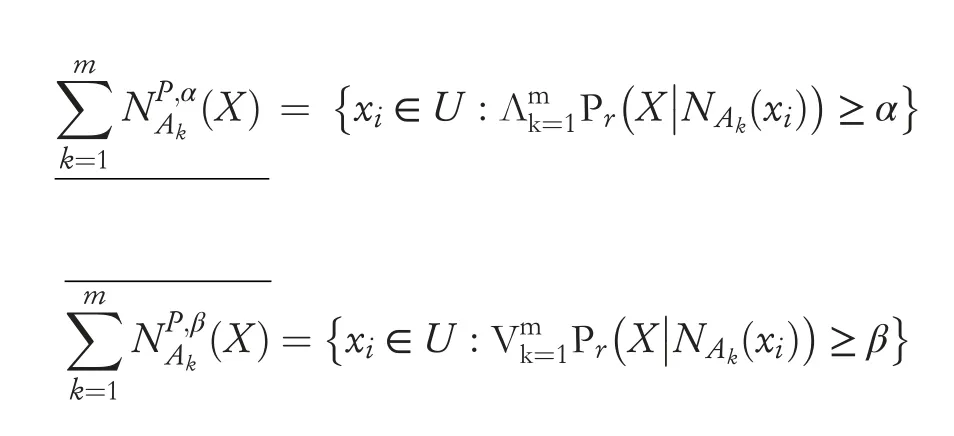
By Definition 3,Definition 4 and the decision rules in the decision-theoretic rough set model,the positive domains,negative domains and boundarydomains based on the optimistic NMG-DTRS model can be,respectively,formalised as follows:

The positive domains,negative domains and boundary domains based on the pessimistic NMG-DTRS model can be,respectively,formalised as follows:

Definition 5Suppose NIS=（U，A=C ∪D，V，f）be a neighbourhood decision table information system,where U represents the target space objects,U=｛xi｜i=1，2，…，n｝ andA1，A2，…Am⊆Aare m granular structures.OrderπD=｛D1，D2，…，Dm｝indicates the partitions on the target space objectsUwith respect to decision space setD∈A,for∀Di⊆πDand thresholds（α，β）,orderdenote the positive decision domains ofDiin the pessimistic and optimistic NMG-DTRS model,then we have the positive decision domains with respect toπDin the pessimistic and optimistic NMG-DTRS model as follows:

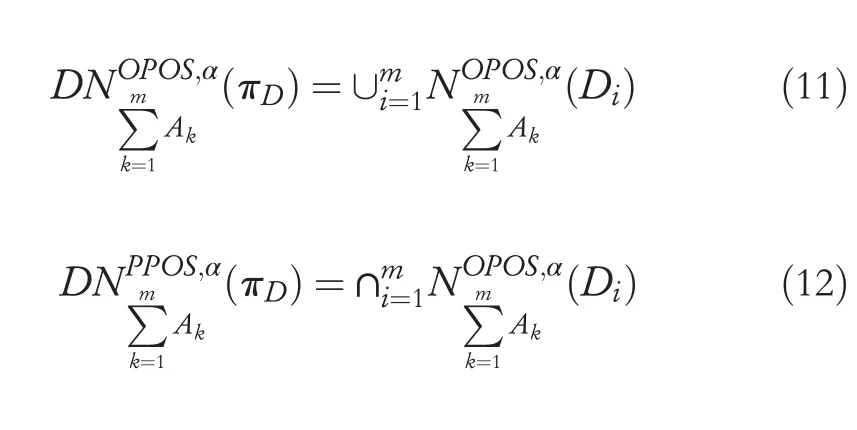
3|MATRIX‐BASED APPROACH FOR NMG‐DTRS

Matrix is a commonly used tool in mathematics and has the characteristics of easy representation and calculation,which can improve the computational efficiency in practical application.Therefore,matrix-based techniques play an important role in knowledge representation and data analysis [20,25].In this subsection,a matrix-based approach was introduced for calculating approximation sets of the NMG-DTRS model and the positive,boundary and negative domains were constructed from the matrix perspective in numerical type or hybrid-valued type decision systems.

3.1|Matrix‐based decision domains expresentation

Definition 6[20,25] Suppose NIS=（U，A=C ∪D，V，f）be a neighbourhood decision table information system,where U represents the target space objects,U=｛xi｜i=1，2，…，n｝,for any object subsetX⊆U,order F（X）is the characteristic function of the subset X,F（X）can be constructed by F（X）=[f i]n×1,where F（X）is a Boolean vector andf ican be expressed as follows:

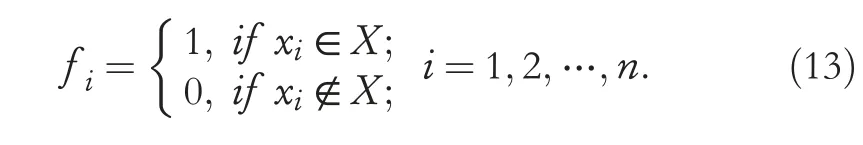
Definition 7Suppose NIS=（U，A=C ∪D，V，f）be a neighbourhood decision table information system,where U represents the target space objects,U=｛xi｜i=1，2，…，n｝,A1，A2，…Am⊆A are m granular structures,orderis the neighbourhood relation matrix about granular structureAk,where（k=1，2，…，m）.For given the neighbourhood radiusδ（δ≥0）and the metric function △,MAkis constructed as follows:

whereminandmaxoperations take the minimum and maximum values.

3.2|The related properties of NMG‐DTRS model

Based on the Definition 3,Definition 4,Definition 9 and the calculation formulas of decision domains of the optimistic and the pessimistic NMG-DTRS model,the related properties of the neighbourhood multigranulation approximation expressed based on matrices can be obtained.

The following lemma regarding the positive domain matrices of the optimistic and the pessimistic NMG-DTRS models can be obtained.

Lemma 1Given neighbourhood decision table information system NIS=（U，A=C ∪D，V，f）,where U represents the target space objects,U=｛xi｜i=1，2，…，n｝.Order πA=｛A1，A2，…Am｝⊆Aare m granular structures,for the given thresholds0.5 ≤α1＜α2≤1and two object subset∀X ⊆∀Y ⊆U,then we can get the following properties:

The relevant proof is omitted.

Lemma 2Given neighbourhood decision table information system NIS=（U，A=C ∪D，V，f）,where U represents the target space objects,U=｛xi｜i=1，2，…，n｝.Order πA=｛A1，A2，…Am｝⊆Aare m granular structures,supposeA1′⊆A1,for given the thresholds（α，β）,and for any the object subsetX ⊆U,then the following related properties can be obtained:

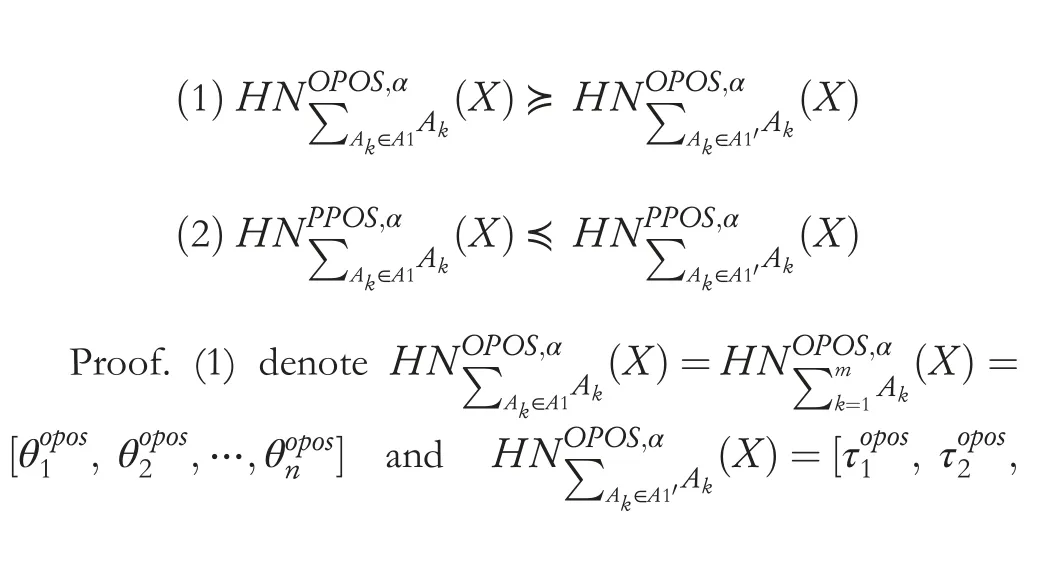
3.3|Algorithm implementation for solving decision domains in NMG‐DTRS

and the pessimistic positive domain,boundary domain and negative decision domain matrices based onπDin NMGDTRS model can be defined by the following:

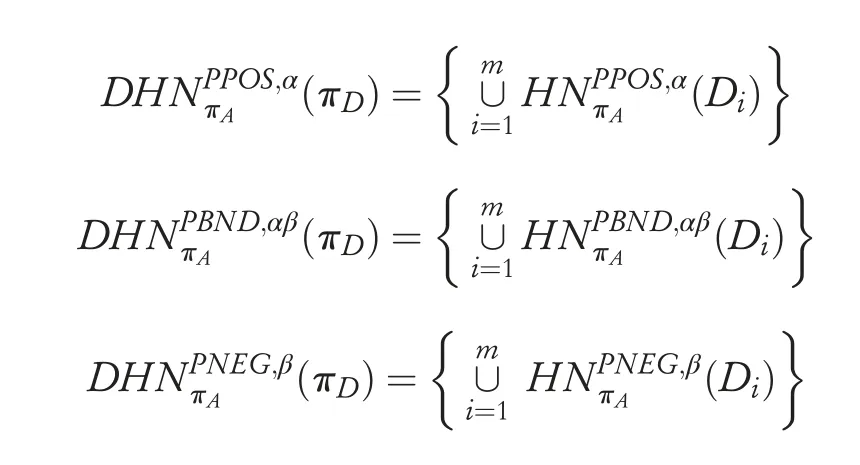
where ∪denotes the disjunction (OR) operations of matrices.

Definition 12Positive decision recognition rate.GivenNIS=（U，A=CUD，V，f）be thee neighbourhood decision information system,whereπA=｛A1，A2，…Am｝⊆Aare m granular structures,D is the decision attribute andπD=｛D1，D2，…，Dn｝ are the partitions on the target space objectsUabout decision attributeD.Orderis the matrix of the positive regions ofπDwith respect toπA,then Positive decision recognition rate in NMG-DTRS model can be defined by the following:

According to Definition 11 and 12,Matrix-based algorithms for decision regions in NMG-DTRS can be described as algorithm 1,algorithm 2 and algorithm 3 in Figures 1-3.

In Algorithm 1,suppose the number of attributes is|C|,for each granularity Ai∈A′，the calculation of the neighbourhood relation matrix and the basic matrix have to be executed,namely the maximum time complexity computing the neighbourhood relation matrix is O（｜C｜·｜U｜2）,and the time complexity of calculating the decision domain matrices under the granularity Aiby Algorithm 2 is O（｜U｜2）,so,the time complexity of step 6-9 in Algorithm 1 is O（m·｜C｜·｜U｜2）,and the time consumption for executing the repeat loop operation in step 10-12 is O（｜U｜2）.Therefore,for all decision partition objects U/D=｛D1，D2，…，Dn｝,the total time complexity of Algorithm 1 isO（mn·｜C｜·｜U｜2）.

In Algorithm 3,the positive decision region matrices DHNOposand DHNPposbe first executed in view of Algorithm 1,we can get the time complexity is O（mn·｜C｜·｜U｜2）,and the time complexity of step 3-5 is O（｜U｜）.Thus,the total time complexity in Algorithm 3 is also O（mn·｜C｜·｜U｜2）.

4|EXPERIMENTAL ANALYSIS

FIGURE 1 Matrix-based algorithm for decision regions

FIGURE 2 Computing decision domain matrices

FIGURE 3 Solving positive decision recognition rate

TABLE 1 Neighbourhood information system

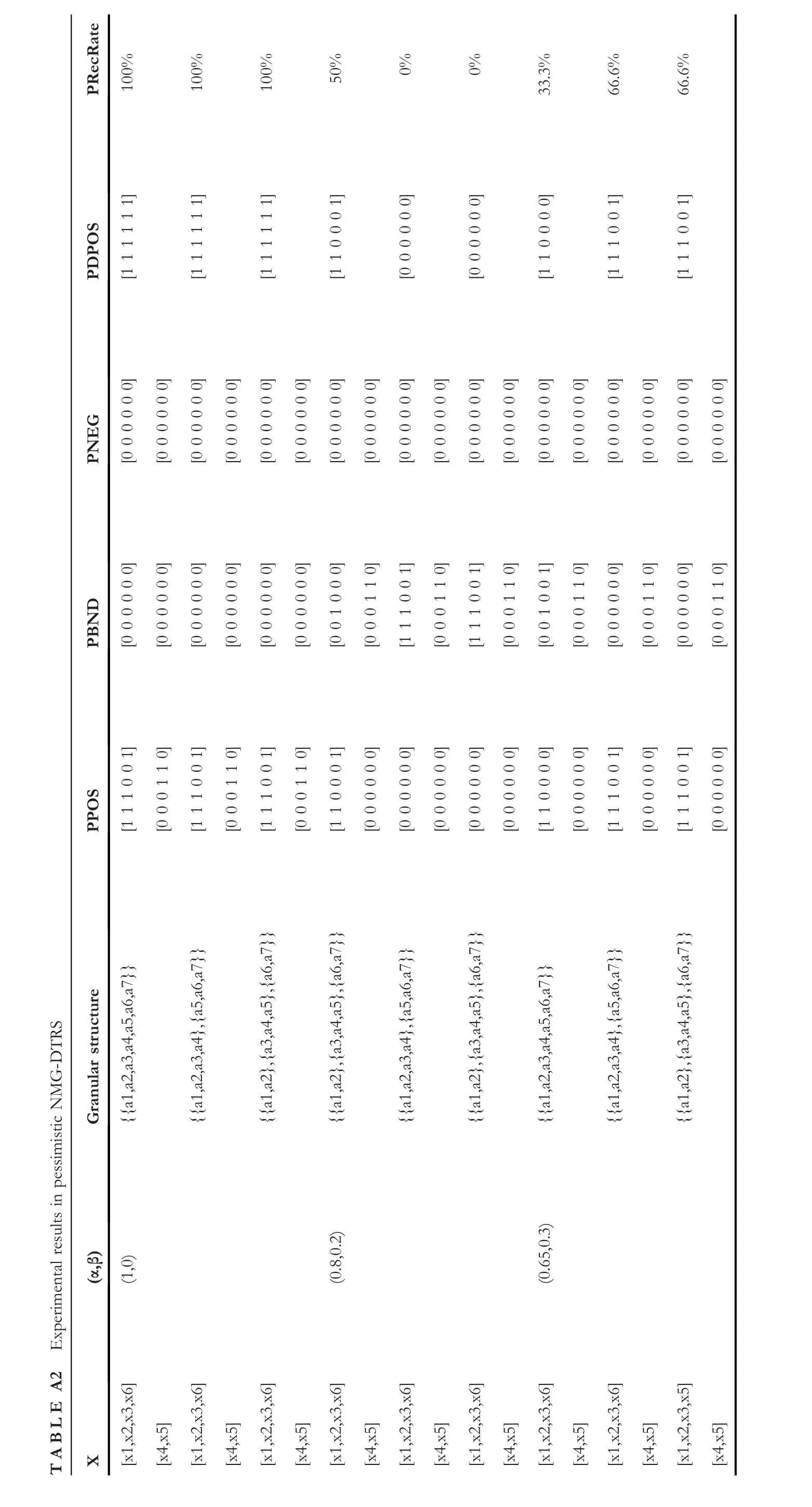
For given a decision table neighbourhood information system NIS,which was shown in Table 1,where U=｛x1，x2，…，x6｝indicate the objects of decision system,A=｛a1，a2，…，a7｝denotes attributes,D is the decision attribute,and decision partition object sets on the universe U based on decision attribute D are ｛x1，x2，x3，x6｝ and ｛x4，x5｝.In the process of the experiment,assume the neighbourhood radiusδ=0.15,and three different granularity spaces were selected for the experiment when the threshold（α，β）is (1,0),(0.8,0.2) and(0.65,0.3),respectively.All the experimental results were gained from Table 1 in python3.6 programming environment,and the experimental results were shown in Tables A1 and A2(see Appendix A for Tables A1 and A2).For convenience of expression,in the Table A1,OPOS,OBND and ONEG denote positive,boundary and negative decision domain matrices obtained in optimistic NMG-DTRS,and ODPOS and ORecRate denote the positive decision matrices and positive decision recognition rate for neighbourhood decision information system in the optimistic NMG-DTRS model,at the same time,in the Table A2,PPOS,PBND and PNEG denote positive,boundary and negative decision domain matrices obtained in pessimistic NMG-DTRS,and PDPOS and PRecRate denote the positive decision matrices and positive decision recognition rate for the neighbourhood decision information system in the pessimistic NMG-DTRS model.

The experimental results in Tables A1 and A2 show that the method based on matrices proposed in this study can effectively calculate the decision domains of the neighbourhood decision system,and it can also be seen that with the change of threshold and granularity,the decision domains and the decision recognition rate also change.At the same time,it can be analysed in the light of information in the Tables A1 and A2 that the positive decision recognition rate reflects the importance of granularity;on the other hand,the decrease of positive decision is mainly caused by the increase of the boundary domain.Therefore,in the actual decision-making process,we can make a decision again for the instance in boundary domain,so as to increase the reliability of decisionmaking.

In order to further verify the effectiveness and feasibility of the approach,several standard datasets provided in UCI database were selected as the experimental objects,and the specific description of datasets was shown in Table 2.In the process of experiments on four different datasets,under the condition of a certain threshold,the positive decision recognition rates obtained from the optimistic and pessimistic NMG-DTRS models were analysed and compared from theperspective of different granularity.See Appendix B for Figures B1a-f and B2g-l.Through the experimental results of four datasets,we can see that the positive decision recognition rate under different granularity is quite different when a certain threshold is given,and the positive decision recognition rate under the optimistic NMG-DTRS is always greater than or equal to that under the pessimistic NMG-DTRS.At the same time,the relationship between decision domain and threshold was analysed,as shown in Figure A3 (Appendix B for Figure B3).According to g(1),g(3)and g(5)in Figure A3,it can be seen that under certain granularity,the change of positive decision recognition rate with threshold is not obvious in optimistic NMG-DTRS,while the positive decision recognition rate in pessimistic NMG-DTRS is relatively influenced by threshold and granularity.See g(2),g(4)and g(6)in Figure A3.According to the experimental results,we get that the importance of granularity is different,and the contribution to decision-making is also different,so the positive decision recognition rate obtained under different granularity is different.Therefore,when we make decision on a complex hybrid information system,we can make decision analysis from multiple perspectives,and at the same time,we can select appropriate threshold to limit the decision decision-making conditions,so as to avoid the phenomenon of one-time decision-making leading to misjudgement and improve the reliability of decision-making.

TABLE 2 Datasets and granular structures description

5|CONCLUSION

MG-DTRS models can analyse decision-making problems from multi-level and multi-angle,the neighbourhood rough set model has the advantage of processing numerical or hybridvalued data,NMG-DTRS models effectively integrate MGDTRS and NRS models,greatly expanding the application range of MG-DTRS.The study proposed a novel matrix-based method for approximation sets of the NMG-DTRS model and solved the decision domains through a series of matrix calculation,the related properties of the NMG-DTRS model were explored and the implementation algorithms based on the proposed method were designed and discussed in detail.The research of NMG-DTRS models matrix-based in this study makes use of the characteristics of matrix which is easy to calculate and understand,and fully combines the advantages of matrix and MG-DTRS,which effectively solves the decisionmaking problems of complex decision information systems from another aspect and expands the application scope of NMG-DTRS.The use of matrix-based NMG-DTRS models for solving the decision-making problems in big data and dynamic data context will be the target of future research.

ACKNOWLEDGMENTS

The authors of this study sincerely acknowledge the support of the Universities Natural Science Key Project of Anhui Province (No.KJ2020A0637).

ORCID

Jiajun Chenhttps://orcid.org/0000-0003-0477-7442

How to cite this article:Chen,J.,et al.:Matrix-based method for solving decision domains of neighbourhood multigranulation decision-theoretic rough sets.CAAI Trans.Intell.Technol.7(2),313-327(2022).https://doi.org/10.1049/cit2.12055

APPENDIX A

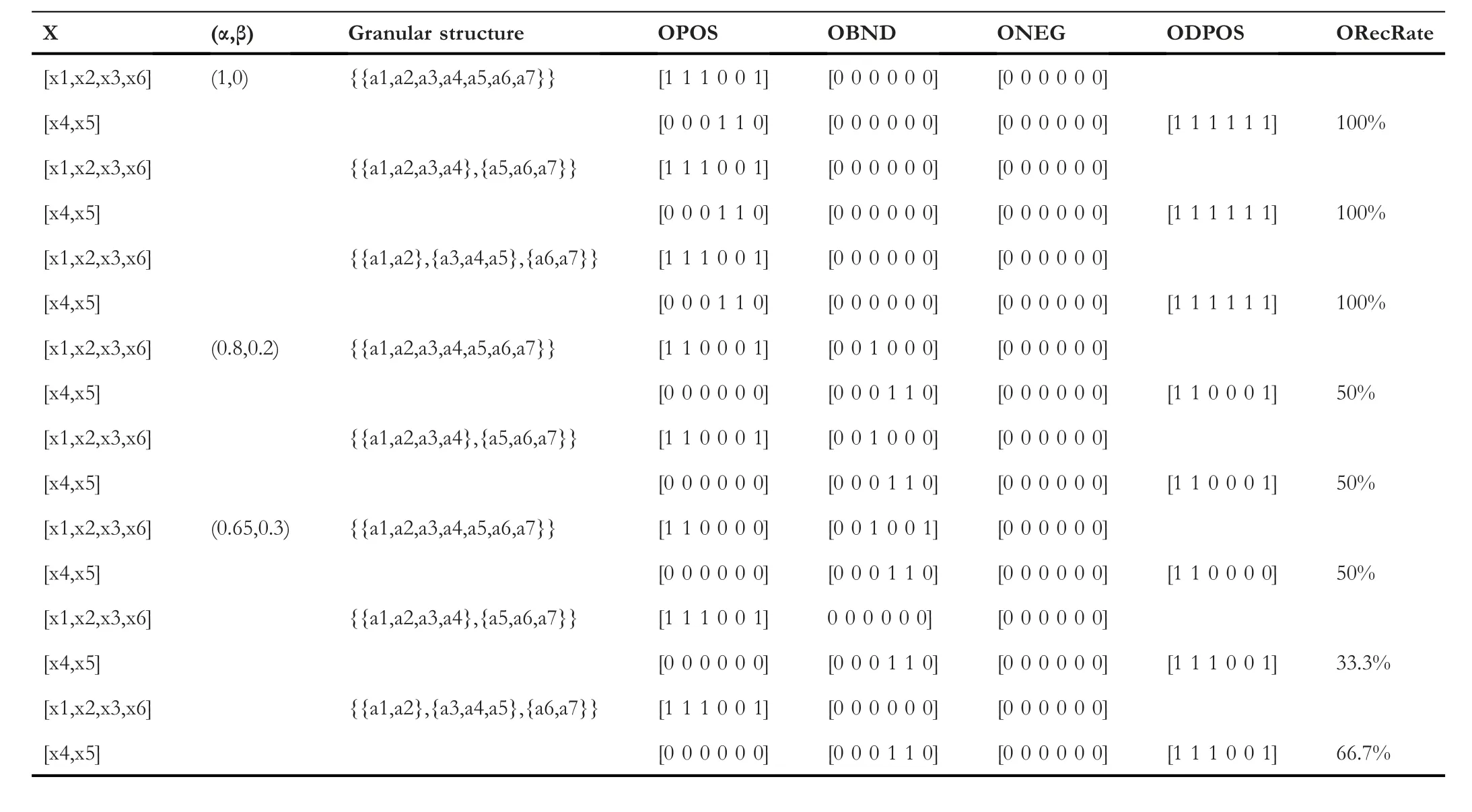
TABLE A1 Experimental results in optimistic NMG-DTRS

APPENDIX B

FIGURE B 1 Comparison of the decision recognition rate in optimistic and pessimistic neighbourhood multigranulation-decision theoretic rough sets

FIGURE B 2 Comparison of the decision recognition rate in optimistic and pessimistic neighbourhood multigranulation-decision theoretic rough sets

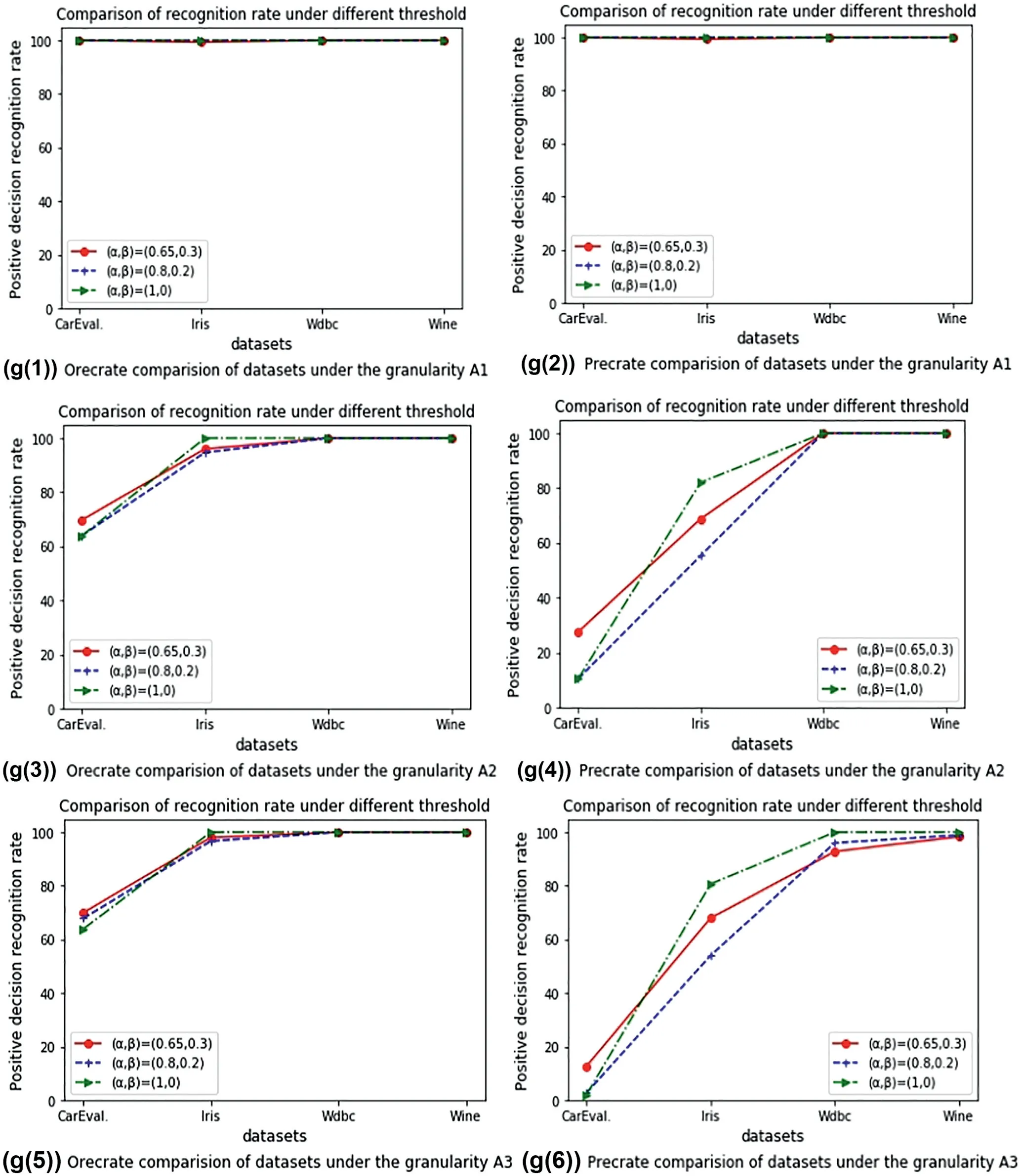
FIGURE B 3 Comparison of the decision recognition rate based on different threshold