Efficient computation of Hash Hirschberg protein alignment utilizing hyper threading multi‐core sharing technology

Muhannad Abu‐Hashem|Adnan Gutub

1Department of Geomatics,Faculty of Architecture and Planning,King Abdulaziz University,Jeddah,Saudi Arabia

2Department of Computer Engineering,College of Computer &Information Systems,Umm Al-Qura University,Makkah,Saudi Arabia

Abstract Due to current technology enhancement,molecular databases have exponentially grown requesting faster efficient methods that can handle these amounts of huge data.Therefore,Multi-processing CPUs technology can be used including physical and logical processors(Hyper Threading)to significantly increase the performance of computations.Accordingly,sequence comparison and pairwise alignment were both found contributing significantly in calculating the resemblance between sequences for constructing optimal alignments.This research used the Hash Table-NGram-Hirschberg (HT-NGH) algorithm to represent this pairwise alignment utilizing hashing capabilities.The authors propose using parallel shared memory architecture via Hyper Threading to improve the performance of molecular dataset protein pairwise alignment.The proposed parallel hyper threading method targeted the transformation of the HT-NGH on the datasets decomposition for sequence level efficient utilization within the processing units,that is,reducing idle processing unit situations.The authors combined hyper threading within the multicore architecture processing on shared memory utilization remarking performance of 24.8%average speed up to 34.4% as the highest boosting rate.The benefit of this work improvement is shown preserving acceptable accuracy,that is,reaching 2.08,2.88,and 3.87 boost-up as well as the efficiency of 1.04,0.96,and 0.97,using 2,3,and 4 cores,respectively,as attractive remarkable results.

KEYWORDS computational biology,high-performance computing,Hyper Threading,pairwise sequence alignment,parallel design,sequence alignment,shared-memory

1|INTRODUCTION

The Multi-processing system is defined as the use of more than one processing unit on a single computer including physical and logical processors(Hyper Threading),which can drastically increase the performance of computers.The multi-core processor system,which represents one of the common multiprocessing architectures,is growing broadly in which,it is extremely difficult to find a computational device without a multi-core processor in the current days.In fact,this design can be useful in the bioinformatics domain as it provides the ability to perform different relevant tasks in parallel by reducing the execution time.Furthermore,the analysis of molecular databases is a time-consuming process since these databases are enormous in their sizes and are still growing.Applying the capabilities of the multi-core architecture in managing the molecular databases and analysis is required for reducing the execution time.

On the other hand,the hyper threading technique is used to increase the capability of a single processing unit that can manage more than one thread at a time[1].This ability allows a single processing unit to handle more than one task concurrently based on an appropriate operating system.Each task is allocated with a particular time frame of execution so that it complies with the entire task,which gives the impression that they are executed in parallel or at the same time.

The molecular sequences analysis and management research field are increasingly attracting the interest of many researchers.With the aid of current technologies in molecular sequencing,the size of molecular (protein,Deoxyribo Nucleic Acid (DNA) [2],and Ribo Nucleic Acid (RNA) [3]) databases are increasing enormously.UniProt (Universal Protein Resource),RCSB (Research Collaboratory for Structural Bioinformatics),and EXPASY (Expert Protein Analysis System)[4-6] are examples of different protein database websites that demonstrate the growth of the database size.The rapid growth of molecular databases drives the need for efficient methods to manage and control large amounts of molecular data sizes[7].This growth of file sizes witnesses serious challenges and motives for researchers to propose faster and efficient sequence comparison methods for controlling,analysing,and organizing these sizes of daily emerging data.

The Sequence Alignment (SA) method is used widely in order to compare sequences as it rates the similarity and distances between various molecular sequences.The calculated similarity may work as an indicator of structural,functional,or evolutionary relationships that the sequences share [8].The pairwise sequence alignment method is a SA method that computes the similarity/distance between two sequences based on calculating the matched blocks of amino acids between the two sequences.

The pairwise sequence alignment method has a significant role in building the guide tree by filling the distance matrix(DM),which facilitates the process of constructing the Multiple Sequence Alignment (MSA) algorithm [9].Such an accurate pairwise sequence alignment contributes directly to improving and speeding up the process of building the MSA.Constructing DM costs (n^2-n)/2 pairwise sequence alignments [10].In particular,a pairwise sequence alignment with high time performance could speed up the process of building DM more efficiently,which,in turn,speeds up the constructional tree guidance leading to faster construction of the MSA algorithm.

Developing fast and accurate sequence alignment methods have been the main challenge for many researchers.A large variety of methods have been proposed in order to achieve optimal results without sacrificing the time performance.

The Smith-Waterman [11] method is a pairwise sequence alignment method,which attempts to reach an optimal alignment where it can,however,sacrifice the execution time as it takes a time of O(mn)to build the alignment between any two sequences.Furthermore,the N-Gram-Hirschberg (NGH)method [12],which is an extension to the Hirschberg algorithm,aims at reducing time and,meanwhile,producing similar results to the results produced by the Smith-Waterman method.Additionally,two methods are presented as an enhancement to the NGH called H-NGH [13,14] and HTNGH [15].The H-NGH method enhances the execution time but at the cost of accuracy.On the other hand,the HTNGH method,which is an enhancement of both former methods:NGH and H-NGH,proposes a further execution time improvement.This work proposes a method that allows the usage of the current high-performance architectures for the purpose of improving the execution time performance of the HT-NGH method.

Even though pairwise sequence alignment algorithms attain optimal results in terms of accuracy[11,12,16],they are considered as time-consuming methods due to the large volume size of data.The NGH algorithm [12] attempts at decreasing the time and the space that is needed to construct the alignment.To compare two protein sequences,it takes O(mn/k),wherekis term size.The highest results are obtained whenkreaches 2 [12].As molecular databases grow rapidly,the need for faster algorithms is becoming an urgent necessity.

This paper studies the effects of using the capabilities of the multi-core architecture in the HT-NGH algorithm's time performance.Additionally,this paper studies the effects of using the Hyper Threading technique (applying multiple threads to each core concurrently)on the parallel performance of this design.Each set of experiments is assigned with different numbers of threads in order to recognize any differences in performance.Finally,the findings are discussed and analysed in terms of the time enhancement between the parallel and original algorithms,including the effects of applying the Hyper Threading on the overall performance.

The outlines of the rest of this paper are organized as follows.Section 2 presents the related research that has been extensively investigated to solve and improve the SA problem.Section 3 explains the problem domain including the newly proposed algorithm.Section 4 demonstrates and discusses the experimental results of the proposed algorithm.Finally,Section 5 gives a conclusion about the proposed algorithm and draws the conclusion and future research pertaining to this study.

2|RELATED RESEARCHES

The pairwise sequence alignment method is used in order to compare two sequences by aligning them in a way that shows the set of similar blocks of amino acids between the sequences.The unmatched amino acids are shifted by gaps or set to face each other within the sequences.To reduce the number of gaps,a penalty is added to the final score of the alignment.A massive number of researches along with a large diversity of methods were conducted to overcome and develop the pairwise sequence alignment challenge.Accordingly,the related researches section shows the main and leading pairwise sequence alignment methods and discusses their main significant characteristics.Additionally,this section shows and discusses the former methods pertaining to this research.In this work,different pairwise sequence alignment methods are classified based on the approach that is used to solve the problem incurred in many different heuristic-based and DPbased methods.

2.1|Heuristic‐based methods

The methods that follow the heuristic approaches tend to look for all achievable solutions and pick the best ones based on a number of criteria that is set in advance.Although the selected solution is considered as the best solution in comparison with the solution pool,reaching the optimal solution is considered a great challenge towards several heuristic approaches.Meanwhile,the methods that apply heuristic approaches are seen to be fast and give results in a reasonable time.This section discusses the main methods that adapt the heuristic approaches in order to solve the pairwise sequence alignment problem.

FAST-All (FASTA) [17] is a pairwise sequence alignment method that utilizes different heuristic approach capabilities for the purpose of aligning and comparing any involved sequences.The proposed method splits the sequences into a number of blocks and then searches for any matched blocks.Every block point to a K tuple,which represents the number of matches between sequences,is used to calculate sequences'resemblance and construct the alignment [18-20].After that,the BLAST (Basic Local Alignment Search Tool) method is proposed to enhance the sensitivity in the FASTA method including the time performance [21,22].Furthermore,the Sequence Search and Alignment by Hashing Algorithm(SSAHA)is proposed to overcome this problem by applying a hash table technique in order to keep track of the K-tuple appearances [23].In [24],an enhanced particle swarm optimization (PSO) algorithm is proposed to solve the pairwise sequence alignment problem.The gp-ALIGNER method[25]presents the segment-based DNA pairwise sequence alignment method that applies an alike score schema as DIalign-T [26]method.A local pairwise sequence alignment[27]is presented in order to reach an optimal un-gapped alignment.

2.2|Dynamic‐Programming‐based methods

Many researchers employ the Dynamic Programming (DP)approach in order to build and improve the efficiency of the pairwise sequence alignment methods.In fact,the Needleman-Wunsch method [28] is considered as the first algorithm that uses the DP approach in solving the sequence alignment and comparison problems.In particular,it computes the resemblance between the sequences by constructing a matrix,called the similarity matrix,which is filled based on another matrix called the substitution matrix[29,30].Constructing the matrix reserves an O(MN) space,which is a considerable amount if the length of sequences is applied.

As a response to Needleman-Wunsch space issues,the Hirschberg algorithm [16] attempts at reducing the space requirement to O(min (m,n)) such that it decomposes the similarity matrix into two matrices.After that,it starts filling the matrix from top and bottom,independently.

In 1981,the Smith-Waterman algorithm is proposed as an improvement to the local pairwise sequence alignment method.In fact,this algorithm is seen to be similar to the Needleman Wunsch algorithm,but except that it has some similarities between suffixes.To seek optimal accuracy,the Smith-Waterman algorithm sacrifices the issues related to time and space[11,17].Additionally,an extended version of the Smith-Waterman algorithm,namely,the N-Gram-Smith-Waterman method [31],is proposed to tackle the time and space issues related to the Smith-Waterman algorithm without the need to decrease its sensitivity.

The Hirschberg algorithm [16],which applies the DP approach for solving the pairwise sequence alignment method,is proposed with the aim of improving the space complexity.In[12],further refinements are performed along with the Hirschberg algorithm by proposing the N-Gram-Hirschberg(NGH),which aims to provide further space and time enhancements.In fact,the NGH algorithm enhances the Hirschberg algorithm based on three stages by starting to reduce the alphabet of the protein amino acid to 10 alphabets,and by cutting the sequences into terms based on the use of the N-Gram method and,finally,converting the terms into integer numbers.

Another method named Hashing-N-Gram-Hirschberg(HNGH) [13,14] is presented in order to provide further enhancements to the time performance.The method improves the NGH algorithm by enhancing the transforming stage(converting the words into an integer)by using the capabilities of the hash function.In fact,this function is used to convert the words that are generated by the N-Gram method into integer numbers,which speed up the comparison process and the alignment.Although the H-NGH algorithm enhances the time performance of the NGH algorithm,the accuracy is decreased,which is following the Hashing philosophy[32],but for pure security,similar to Hashing text authentication [33]and mobile trust verification [34].

Furthermore,the HT NGH method[10,15]is proposed as a refinement to the NGH and H-NGH methods with the aim of building DM,which is used to construct several multiple sequence alignments.The proposed method uses the capabilities of the hash table in order to improve the performance of the transformation stage in the NGH and H-NGH methods.In conclusion,the proposed algorithm outperforms its former methods and demonstrates an improved accuracy and execution time.In addition,a proposed method for executing the HT-NGH method in parallel is discussed in [35].

Lately,many research methods[36-47]have been conducted for the purpose of improving the efficiency and performance of the pairwise sequence alignment through wide diversity.Despite the fact that the DP-based pairwise sequence alignment algorithms have reached an optimal alignment,reaching a high time performance remains a challenge itself.Many methods such as the NGH,H-NGH,and HT-NGH methods have been produced to reduce the execution time when the time performance can be further improved.In this research,a parallel computing method is proposed for more improvement in the time performance of the HT-NGH method.

3|PROBLEM DEFINITION

This research presents a parallel algorithm that combines multi-core shared memory architecture with the Hyper Threading technique in order to test the performance effects of Hyper Threading on share memory modelling.The HTNGH pairwise sequence alignment algorithm is used as a case study.It is used to construct the distance matrix.The construction of DM is accomplished in two stages.The first stage is based on transforming the alphabet of the protein sequences from 20 amino acids represented by 20 different characters into 10 integer numbers.The second stage is based on building the pairwise sequence alignment and constructing the matrix.This research focusses on speeding the first stage by utilizing the capabilities of the shared memory architecture and multi-threads technique.

Each protein sequence passes through several reforming levels leading to sequences that are shorter and easier to be compared.This stage consists of many phases starting with the protein sequence alphabet reduction and passing through further reduction of sequences by dividing them into terms(words) and ending by converting the terms into integer numbers based on the use of a hash table.

The alphabet of the protein sequences consists of 20 amino acids,where each amino acid is represented by a character.The protein alphabet reduction phase is done by applying some sort of clustering to the 20 amino acids based on the similarity of their properties such as physicochemical properties [48,49] where those amino acids can be grouped together.After the completion of this phase,the 20 amino acids are distributed along into 10 clusters represented by numbers ranging from 0 to 9 where the protein sequences are represented by 10 numbers such that each number refers to a group of amino acids.

Splitting the sequences into terms is performed by applying the N-Gram method(see Table 1).All the terms have the same length while the term size is set earlier.The term length ranges from 2 to 5 amino acids.The final phase in the sequence transformation stage is to convert the term into numbers in which each term is represented byone integer value instead of having N integer numbers(N is the term length).

The HT-NGH algorithm uses the hash table technique in order to convert the involved terms from a group of numbers to an integer value.This process is conducted by using a multidimensional array of size 10N,whereNrefers to the term size,which represents the hash table.The main purpose of the array with such a size is to give enough space to assign a unique integer value for every term.The array containsMdimensions whereMis equal to the word's(term)length.Every dimension in the array is associated with a number(letter),which fastens and simplifiesthe process of addressing the terms within the array.So,every combination of letters(word)is assigned with a distinctive value.

TABLE 1 Examples of cutting a sequence S down into terms using N-Gram

Finally,the protein sequences are aligned by applying a pairwise sequence alignment based on the use of the Hirschberg algorithm.The main purpose of the alignment is to build the DM by computing the values of resemblance among the involved sequences.To align the sequences,a similarity matrix is constructed and filled with the similarity values between the amino acids.Equation (1) is used to calculate the similarity values between amino acids in order to fill the similarity matrix appropriately.

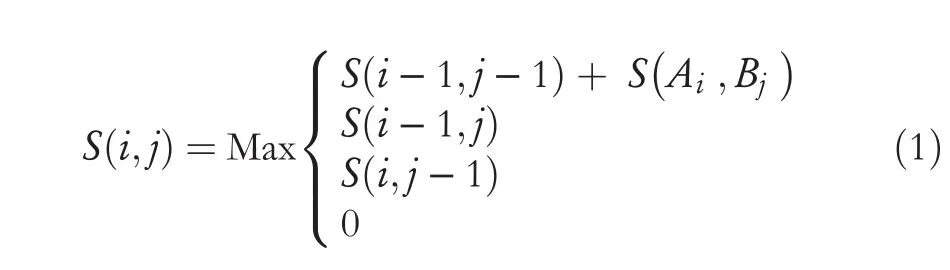
A full pairwise sequence alignment is conducted,where each sequence is aligned against all other sequences in the dataset in order to build DM.Algorithm 1 demonstrates the transformation phase of the HT-NGH method.

On the other hand,calculating the distances between the two protein sequencesS1andS2is carried out by using Equation (2).

4|METHODOLOGY

This paper proposes an algorithm that exploits the performance capabilities of parallel designing in order to test the performance effects of Hyper Threading on shared memory architecture and speeds up the HT-NGH algorithm.The Single Instruction Multiple Data (SIMD) modelling is used to manage the parallel process where the data is decomposed in such a way that each core is assigned with a protein sequence at a time when processing units are used more efficiently.Furthermore,this approach splits the data into different subdatasets.After that,it manages these datasets by using the same piece of code.

4.1|The parallel algorithm

In order to parallelize the HT-NGH algorithm,the problem is decomposed into a data level where each core is assigned with a protein sequence at a given time.The algorithm is implemented using C++and parallelized using the Mingw32 OpenMP library.Figure 1 shows the data decomposition architecture of the parallel algorithm where the sequences transformation algorithm is applied by all cores through different datasets.

4.1.1|Architecture

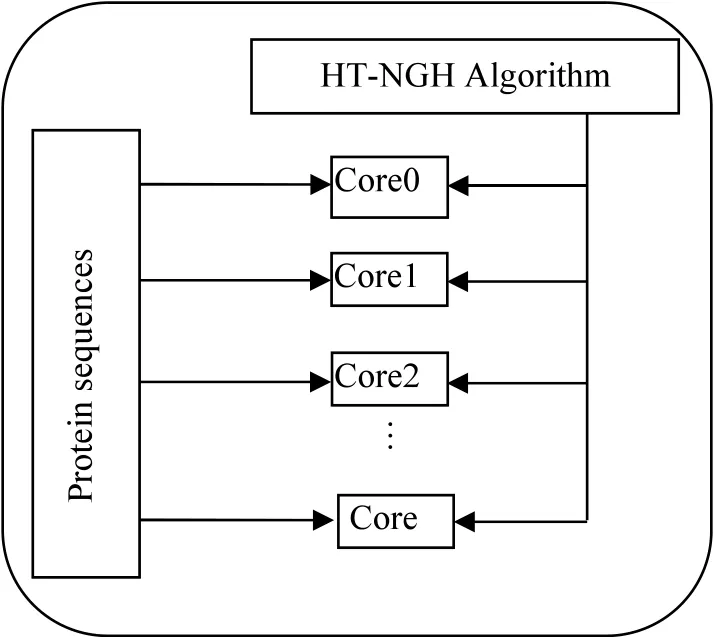
FIGURE 1 Data decomposition architecture

The parallelarchitectureisbasedonthemulti-coresdesignwhere the quad-core processor is used accordingly.Figure 2 highlights a schematic diagram of the parallel modelling.On the other hand,the SIMD architecture is used to manage different parallel processes.SIMD architecture is applied mainly on three phases;transform the sequence of characters to a sequence of integers phase,cutting sequence into terms phase,and converting the term into integers phase.This design is applied to manage the decomposition process since the aim is to distribute the dataset over the cores,which are executing the same code(task).

4.1.2|The decomposition method

In this research,data decomposition is used where the dataset is decomposed into a number of blocks and sent along to the cores.The number and size of the blocks are determined based on the dynamic load balancing technique.

The dynamic load balancing technique is used with chunk size equals one to balance the loads among the cores where the number of blocks is increased at the time the size of the blocks is decreased.Each core receives a single protein sequence at a time.In fact,employing such a technique would increase the communication overhead among the cores due to the increasing number of data blocks.Additionally,faster cores get more sequences to process than slower cores,which lead to providing more effective use of processing units since there are no idle cores during the processing time.Moreover,the size of protein sequences varies from around 100 amino acids to thousands of amino acids.When using a fixed size of blocks,the entire cores obtain the same number of protein sequences that would slow down some cores.The reason behind this is that protein sequences do not share the same length and implies that some cores should handle longer sequences compared to other cores.Figure 3 illustrates the database partitioning process and Figure 4 shows the overall flowchart of the proposed method.

5|ANALYTICAL EXPERIMENTS AND FINDINGS

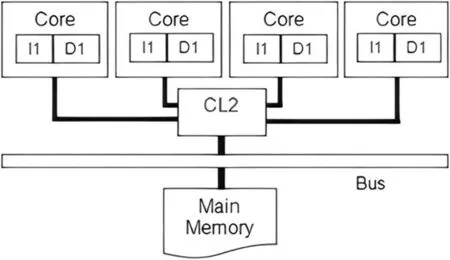
FIGURE 2 Schematic diagram of Intel quad-core architecture [50]

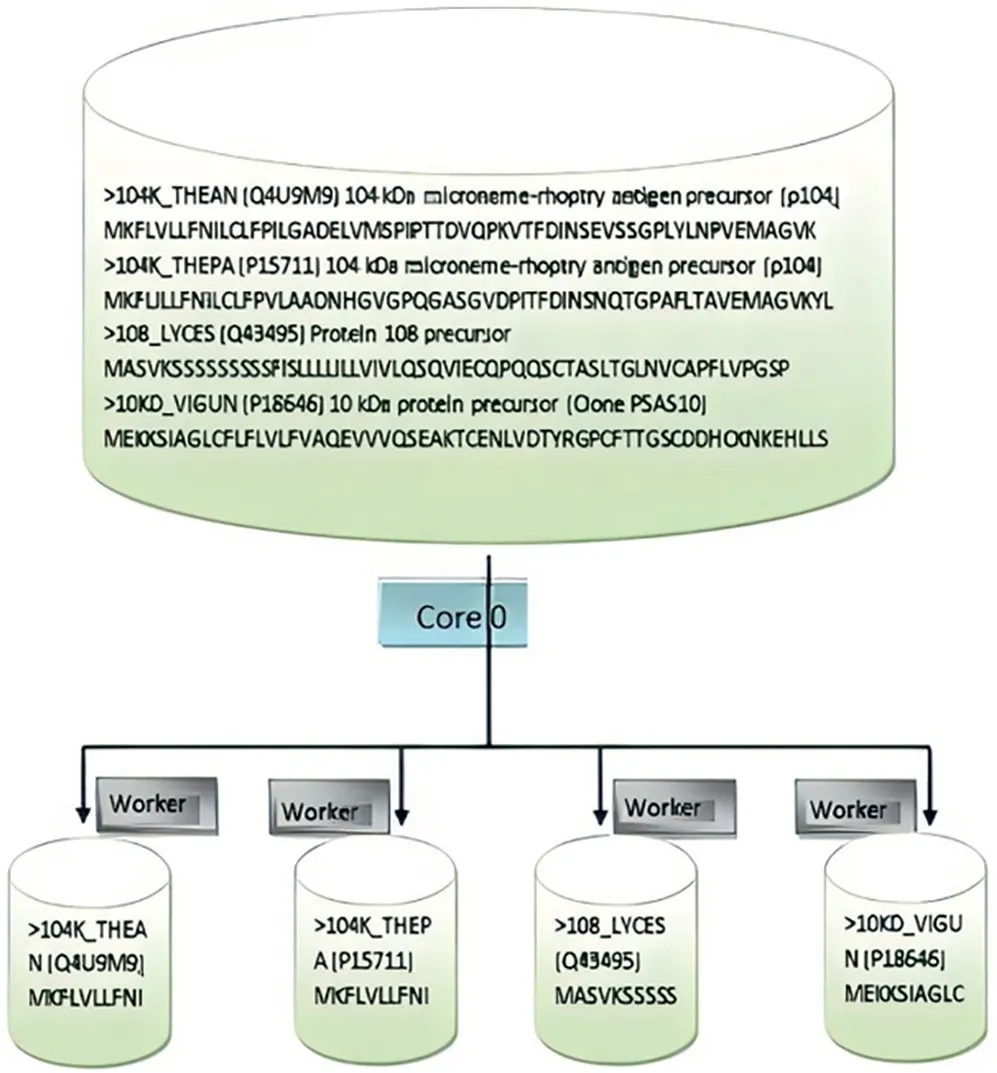
FIGURE 3 Dataset partitioning process

To evaluate the proposed algorithm,a Swiss-Prot database[6]is used in the FASTA format.The proposed algorithm is tested based on the use of various inputs of data.The variation of these inputs relies on the number and length of the involved protein sequences.The results are assessed in terms of the accuracy and execution time performance.In fact,the accuracy is assessed by comparing the results of the proposed method with the obtained results of the original method.Moreover,the time performance is evaluated by computing the speedup,efficiency,and gained performance.Seeking for better performance,the Hyper Threading technique is used where each core is assigned a number of tasks that is divided into multiple threads concurrently.The speedup of the shared memory parallel algorithm alone without using hyper threading is compared with the speed up of the parallel algorithm after applying the hyper threading technique.Consequently,this section discusses the hardware and software specifications,results measurements,datasets,time performance and accuracy in detail.

5.1|Hardware and software specifications

The experiments are run on an Intel®Core™i7-8550U multicore processor with an 8 GB RAM.The processor consists of 4 cores and the type of the system is 64 bits and supports up to 8 threads using Hyper Threading technology.The experiments are conducted on Windows10 Pro by using the C++on code Blocks 17.12.

5.2|Time performance measurements

The time performance is evaluated by computing the speedup,efficiency,and gained performance.Accordingly,this section discusses how the results are measured

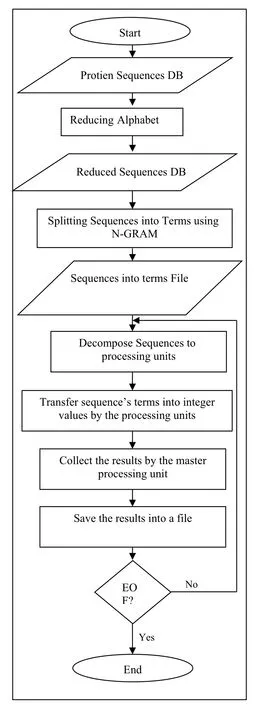
FIGURE 4 Overall flowchart of the proposed method

5.2.1|Speedup estimation

Speedup refers to the performance of the parallel algorithm by relating the parallel algorithm results to the results pertaining to the sequential algorithm.Equation(1)shows how the speedup is calculated.

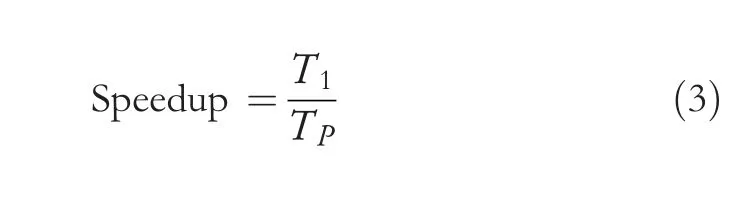
whereT1denotes the execution time for the fastest sequential program when using a single core andT2denotes the execution time of the parallel algorithm when using P cores.

5.2.2|Efficiency estimation

Efficiency indicates whether or not the processing units are effectively employed by splitting the speedup on the number of processing units.Equation (2) highlights the calculation process of the efficiency employment.

wherePis the number of processing units.

5.2.3|Performance gain

Performance increase refers to the percentage of the gained enhancement during the use of the parallel algorithm.Equation (3) shows how the gained performance is calculated.

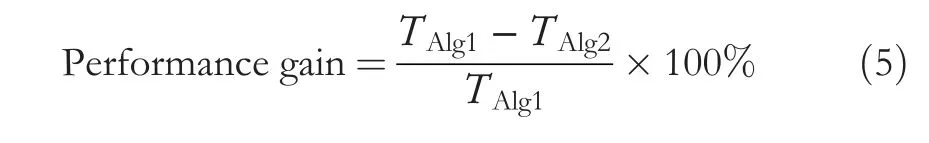
whereTAlg1denotes the execution time of the sequential algorithm,andTAlg2denotes the execution time of the parallel algorithm.

5.3|Testing datasets

The Swiss-Prot database is used as a dataset for testing the proposed algorithm while the protein sequences are represented in the FASTA format.Figure 5 illustrates an example of the protein sequence in the FASTA format.

The proposed algorithm is tested in diverse sizes of dataset parameters.The parameters represent the number of sequences,the database size in megabyte,the term length,number of cores and number of threads.Table 2 shows the ranges of such parameters.

5.4|Proposed multi‐core comparison remarks

The results demonstrate an improved time performance without sacrificing the accuracy as compared with the original algorithm(the HT-NGH algorithm).This section discusses the results in terms of time performance and accuracy,along with the performance's gains of applying the hyper threading technique by assigning multiple threads for each core concurrently.

FIGURE 5 Protein sequences in FASTA format

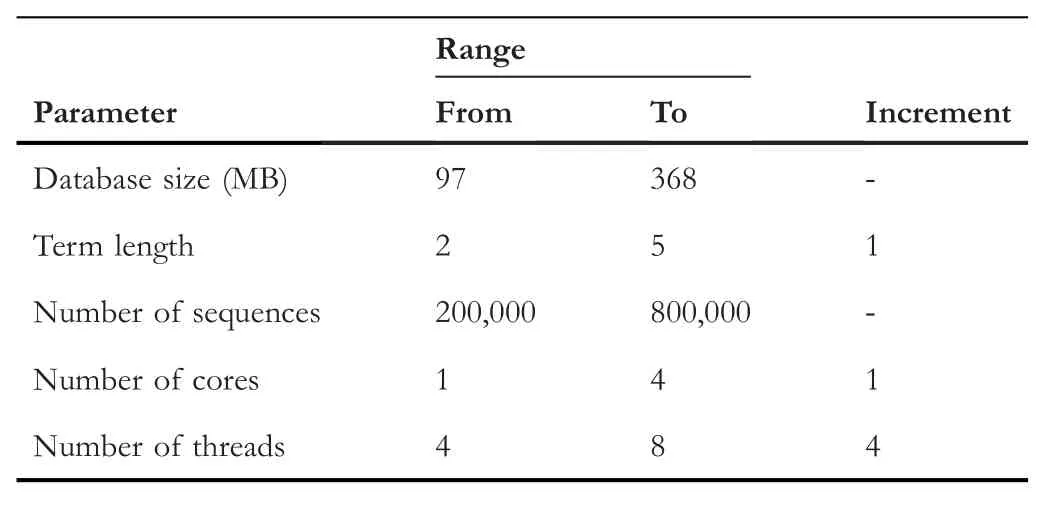
TABLE 2 Experimental parameters and ranges

5.4.1|Evaluation assigning each core one thread at a time

The experiments are divided into two groups that are evaluated based on the time performance.The first group is concerned with the time performance that is gained by assigning one thread for each core at a time (shared memory alone without using hyper threading) in order to test the effectiveness of using the multi-core architecture.On the other hand,the second experimental set is concerned with the time performance that is gained by applying the Hyper Threading technique in order to study the effects of assigning each core multiple threads concurrently on the time performance of the shared memory algorithm.

The experiments demonstrate that the proposed method outperforms the HT-NGH method.The time performance of the proposed algorithm is evaluated by computing the speedup,efficiency and gain performance of the obtained results.

Speedup analysis

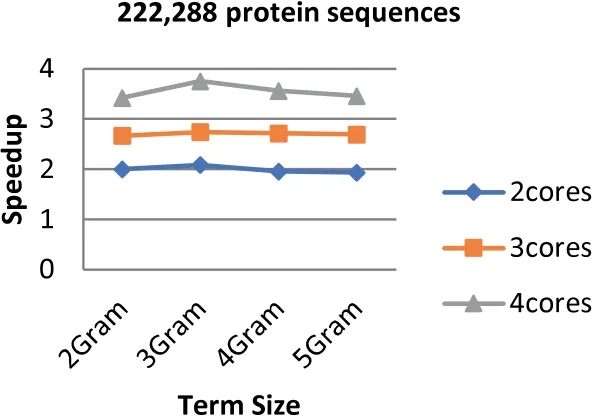
FIGURE 6 Speedup of Parallel HT-NGH algorithm for 97 MB dataset size (200 k Protein Sequences)

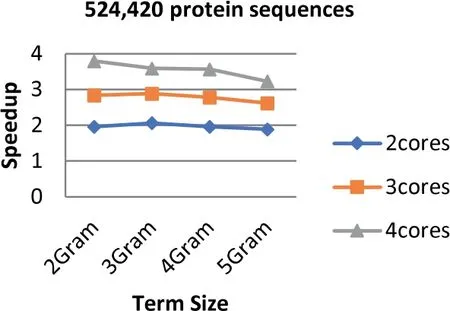
FIGURE 7 Speedup of Parallel HT-NGH algorithm for 234 MB dataset size (500 k Protein Sequences)

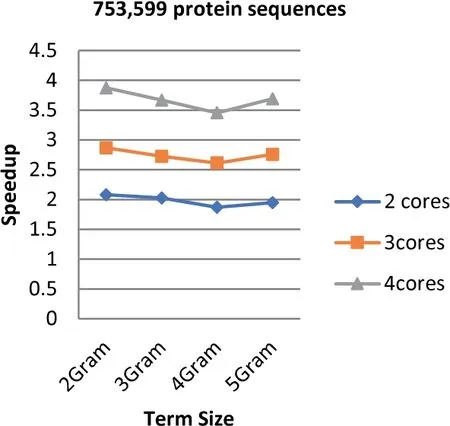
FIGURE 8 Speedup of Parallel HT-NGH algorithm for 339 MB dataset size (753 k Protein Sequences)

Experiments show that the parallel algorithm obtains higher speedup.This enhancement of speed performance is coming as a result of reducing the communication overhead among different cores by providing the cores with the same task to perform.Additionally,load balancing plays an important role in increasing the speed of the parallel algorithm since it allows the algorithm to reach the most effective use of resources (no idle cores).Figures 6-8 show the values of speedup that are taken for the sizes of the dataset that range from 97 to 368 MB,the term ‘length’ ranging from 2 to 5 increments by one,and the number of cores ranging from 2 to 4 increments by one.The results demonstrate that the number of cores has significant effects on the speedup that increases when the number of cores increases.The main reason behind this refers back to the increment in the resources when the number of processing units is increased.Further,the length of the term(word)has a considerable impact on the speedup.The highest speedup is gained when the term size is equal to 2.On the other hand,the size of datasets does not have any considerable impacts on the speedup.The highest speedup is obtained when 4 cores are mainly at a term length that is equal to 2.

Efficiency analysis

The experiments show that the proposed algorithm obtains a high efficiency that is mainly gained due to the high speedup incurred into the algorithm.As shown in Equation (2),the speedup has a significant impact on the efficiency of the algorithm.

Unlike the speedup results,the highest efficiency is obtained when the number of cores is equal to two while the lowest is obtained at 4 cores.The highest efficiency is 1.044 that is obtained based on the term length that is equal to 3(3 g).Figures 9-11 illustrate the values of efficiency that are taken for the sizes of the dataset that ranges from 97 to 368 MB,the term length ranging from 2 to 5 increments by one,and the number of cores ranging from 2 to 4 increments by one.It is shown to be proven from the obtained results that the value of speedup has a great impact on the efficiency score.Additionally,the number of cores has a contrast impact on the efficiency value in which the less cores use the highest gained efficiency values.In fact,this is due to the overhead latency that comes as a result of the increment in communications such as the distribution of the data through to the cores and the gathering of the obtained results from the cores.

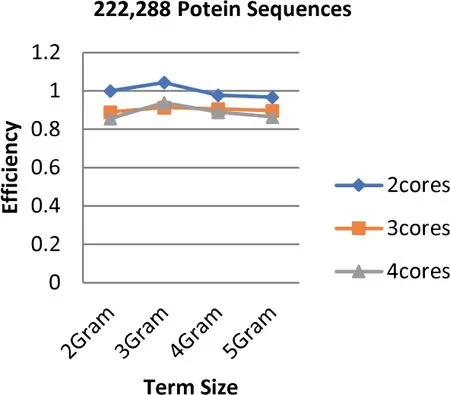
FIGURE 9 Parallel HT-NGH algorithm's efficiency for 97 MB dataset size (200 k protein sequences)

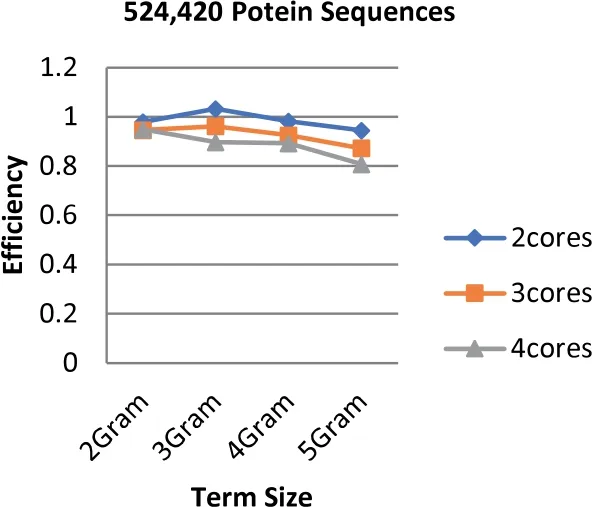
FIGURE 10 Parallel HT-NGH algorithm's efficiency for 234 MB dataset size (500 k protein sequences)

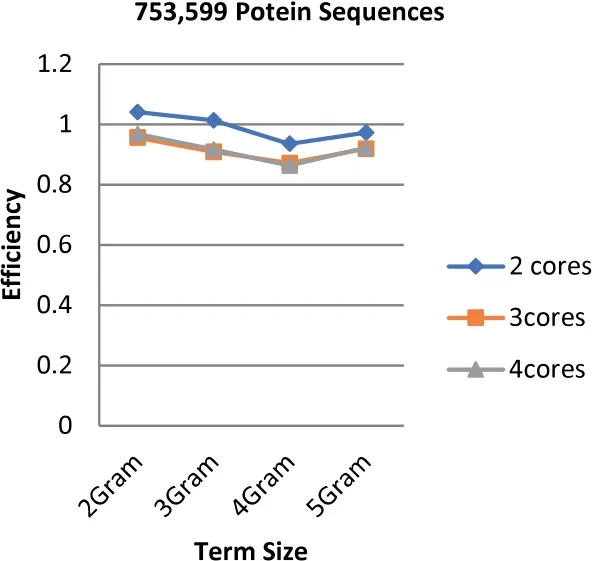
FIGURE 11 Parallel HT-NGH algorithm's efficiency for 339 MB dataset size (753 k protein sequences)

Performance analysis

The experiments show that the proposed algorithm obtains higher gains of performance.The obtained performance gain is mainly acquired because of the high speedup of the algorithm.As noticed in Equation (3),the high speedup leads to higher gains of performance.Figures 12-14 highlight the values of the gained performance that are taken for the sizes of the dataset ranging from 97 to 368 MB,the term length ranging from 2 to 5 increments by one,and the number of cores ranging from 2 to 4 increments by one.As can be seen from these figures,the highest performance gain is 74.19 that is obtained when 4 cores are used along with the term length that is equal to 2.On the other hand,the performance is decreased when the number of cores is also decreased;besides,the lowest performance gain is scored when 2 cores are used.Using more processing units for executing the algorithm leads to a more effective performance gain.

5.4.2|Evaluation applying hyper threading

Hyper threading is assigning each core multiple threads concurrently.This Hyper Threading technique is useful when it manages different required tasks and at the same time,it improves the execution time [1].To run the code in parallel and harvest the multi-core processor's capabilities,the code is divided into a number of threads [51].Furthermore,the processor that is used through the experiment represents a quadcore processor,which supports the Hyper Threading technique that can handle up to 8 threads at a time.To apply the capabilities of the Hyper Threading technique and seek for further improvements in the time performance,each core is assigned multiple threads concurrently.

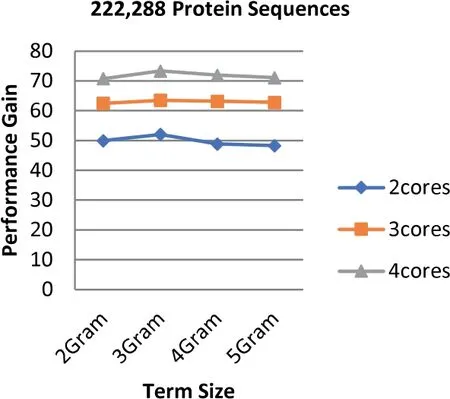
FIGURE 12 Parallel HT-NGH algorithm's performance gain for 97 MB dataset size (200 k protein sequences)

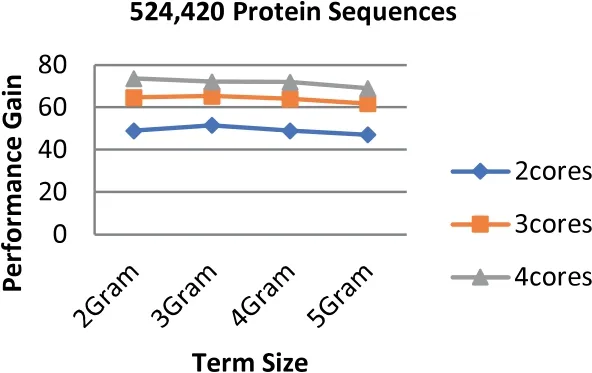
FIGURE 13 Parallel HT-NGH algorithm's performance gain for 234 MB dataset size (500 k protein sequences)

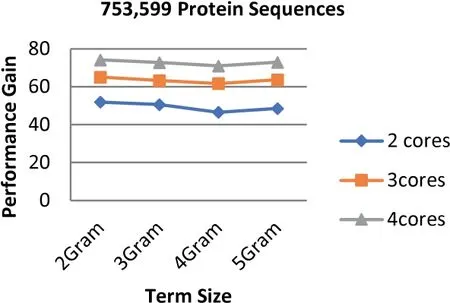
FIGURE 14 Parallel HT-NGH algorithm's performance gain for 339 MB dataset size (753 k Protein Sequences)

The experiments demonstrate that using the hyper threading technique improves the performance of the cores,which in return enhances the time performance of the algorithm.In particular,the time performance is assessed by computing the speedup of the obtained results and comparing them with the time performance that is obtained by assigning one thread for each core at a time.

Figures 15-20 show the speedup that is gained by applying this technique in the parallel algorithm.The results are divided based on the number of cores,the number of threads,dataset size and term length.The number of cores that are used in the experiments is 2 and 4 cores where each core is assigned 2 threads (due to hardware limitations) concurrently.Finally,the size of the datasets ranges from 97 to 368 MB,and the terms length ranges from 2 to 5.The experiments demonstrate that assigning multiple threads for each core concurrently improves the speedup of the parallel algorithm in comparison with the assigned tasks by using one thread at a time.

FIGURE 15 Comparison between speedup gained by applying hyper threading on 2 cores and speedup gained by assigning each core one thread at a time for the 97 MB dataset size (200 k Protein Sequences)

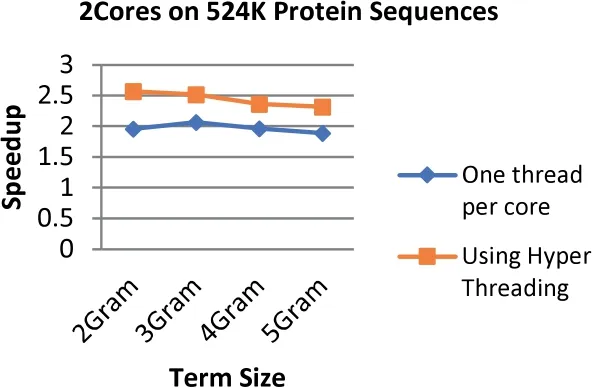
FIGURE 16 Comparison between the speedup gained by applying Hyper Threading on 2 cores and speedup gained by assigning each core one thread at a time for the 234 MB dataset size (500 k Protein Sequences)

FIGURE 17 Comparison between the speedup gained by applying Hyper Threading on 2 cores and speedup gained by assigning each core one thread at a time for the 339 MB dataset size (753 k Protein Sequences)

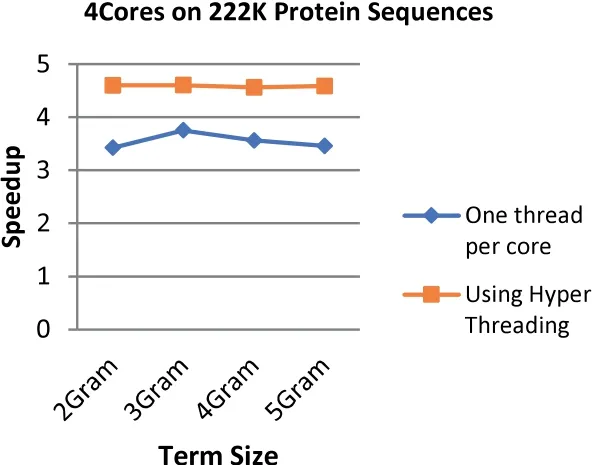
FIGURE 18 Comparison between the speedup gained by applying Hyper Threading on 4 cores and speedup gained by assigning each core one thread at a time for the 97 MB dataset size (200 k Protein Sequences)

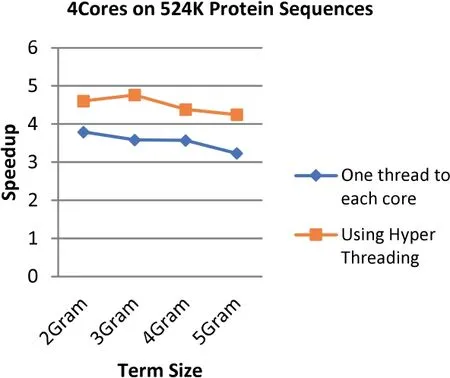
FIGURE 19 Comparison between the speedup gained by applying Hyper Threading on 4 cores and speedup gained by assigning each core one thread at a time for the 234 MB dataset size (500 k Protein Sequences)

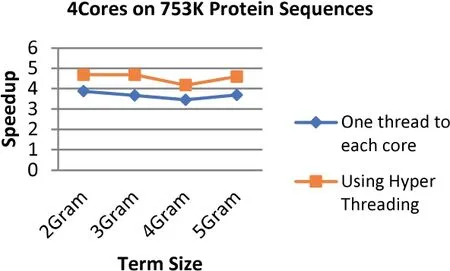
FIGURE 20 Comparison between the speedup gained by applying Hyper Threading on 2 cores and speedup gained by assigning each core one thread at a time for the 339 MB dataset size (753 k Protein Sequences)

The results demonstrate that applying the hyper threading technique increases the speedup up to 34.4%where the highest speedup reaches 4.76 with an increment of 1.77 when using 8 threads on 4 cores at the term length that is equal to 3.On the other hand,the lowest speedup is 2.03 with an increment of 0.17(8.8%)when using 4 threads on 2 cores at the term length that is equal to 4.

In general,the speedup enhancement ranges from 8% to 34%with an average of 24.8%.This enhancement emerges due to utilizing Hyper Threading technique ability to create multiple logical processors by using a single processing unit that is able to increase the performance gains for up to 30%,which are tested on the Intel Xeon processor [1].Furthermore,OpenMP has the ability to avoid most of the overhead issues that are relevant to threads' management [51].

Even though the speedup is increased,the enhancements are degrading at some points due to the encountered overheads latency such as the per-threads (loop scheduling) and lock management.In fact,these kinds of overheads cannot be avoided when using OpenMP [51].Furthermore,the size of datasets does not have any considerable impact on speedup.

5.4.3|Accuracy remarks

To validate the accuracy consistency of the proposed method,we assessed remarks by comparing the results of the proposed method with the results of the HT-NGH technique.The proposed process produced the same results as the ones of the original HT-NGH algorithm,as found fully matched.It is to be noted that this accuracy was not interfered via the decomposing technique that is used,benefiting from the adopted dynamic balancing load affecting data decomposition within sequence level.This parallelization precision is in line with multiplication architecture arrangements presented for Jacobian elliptic curve computation [52]and GF(p) multiple multipliers [53] as well as scalable multipliers parallelization [54].

6|POSSIBLE EXTENSION TO GENOMIC SEQUENCES

It is important to discuss the possibilities of extending and generalizing the applicability of the proposed method to cover other genomic sequences.This section discusses the applicability of generalizing the proposed method to cover all genomic sequences and its effects on performance.Genomic sequences,computational wise,share similar representation as they are represented by a sequence of letters.

The main difference between them is the alphabet where DNA and RNA sequences are represented by four letters while protein sequences are represented by 20 letters [55].This memory sharing strategy can benefit boost-up parallel sharing via counting-based secret-sharing [56] and its enhancement in matrices[57]as well as increasing shares[58],trustfulness hiding[59],and sharing regularity optimization [60].The proposed method can be extended and generalized to cover genomic sequences since,computer-wise,all of them are represented as a string of letters.Furthermore,the proposed method should give the same performance on other genomic sequences as on protein sequences because of the fact that the proposed method applies a dynamic load balancing technique in which each core receives a single sequence at a time leading to the fact that the type of genomic sequence would not be an issue.

Unfortunately,the proposed method cannot be extended or generalized to cover further genomic sequences other than protein testing of this paperwork,since the HT-NGH method has been applied on protein only,similar to pairwise sequence alignment based on transition probability between two consecutive pairs of residues [61] as well as rigid region pairwise sequence alignments [62].The work can further involve engineering Hash functions [63] combined with partitioning of watermarking via counting-based secret sharing[64]as for semicomplete text reliability [65] aiming innovative researches.Accordingly,the proposed computational protein alignment utilizing hyper threading multi-core sharing technology method needs to be extended precisely for other genomic sequences,which are still open research applicable to give independent supplementary remarks.

7|CONCLUSIONS

This paper presents time performance enhancement to pairwise sequence alignment method called HT-NGH to study the performance effects of Hyper Threading over shared memory architecture on the molecular dataset.HT-NGH procedure is an enhancement combination to the H-NGH and NGH algorithms in which the execution time performance has improved preserving acceptable accuracy.The SIMD architecture is used to distribute the data among different processing units where the data is decomposed into a level of sequences.The load balancing method is applied in order to avoid any idle processing units during the execution aiming for fair CPU utilization.

Experiments demonstrate the superiority of the proposed parallel algorithm to gain performance running the HT-NGH algorithm without leaving integrity validation apart.The speedup of using shared memory alone without hyper threading reaches its highest results by using 4 cores while the highest efficiency is gained by using 2 cores.On the other side,for further time performance improvement,Hyper Threading technology is applied.Using Hyper Threading by assigning multiple threads concurrently to each core increases the speed up of the parallel algorithm by 24.8% on average.

This research focusses on the performance effects of Hyper Threading on multi-core architecture as parallel architecture while other parallel designs,for instance,multiprocessors and graphics processing units (GPU),could be tested as well.Furthermore,a suitable combination/hybridization between several different parallel models could have a high impact on the obtained results.In addition,the proposed method could be extended and generalized to cover different genomic sequences other than protein sequences providing expected new research remarks.

ACKNOWLEDGEMENTS

This project was funded by the Deanship of Scientific Research(DSR),King Abdulaziz University,Jeddah,under grant No.D-139-137-1441.We thank motivating this wonderful scientific collaboration between the authors from the Department of Geomatics(King Abdulaziz University)and the Department of Computer Engineering (Umm Al-Qura University),both fully sponsored by the Ministry of Education within Saudi Arabia.Also,we would like to acknowledge that this research is an extended version of the paper presented in [35].

CONFLICT OF INTEREST

The authors declare that they have no competing interests.

INFORMED CONSENT

Informed consent was obtained from all individual participants included in the study.

DATA AVAILABILITY STATEMENT

All supplementary material files that are submitted along with this research paper are for the‘data availability’section to give access to data.Other than that,there are no supplementary material files.The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.Also,data are available at Google Drive folder at the following link:https://drive.google.com/drive/folders/1hJaNW7BMZIBjBeUdErhigdI7K8gPFUog?usp=sh aring

Below is a detailed description of the code and datasets files.

(Continued)

ORCID

Adnan Gutubhttps://orcid.org/0000-0003-0923-202X