逐像素调制的高反光表面三维测量方法

冯 维，徐仕楠，王恒辉，熊 芝，王选择，翟中生

（1.湖北工业大学 机械工程学院,武汉 430068；2.现代制造质量工程湖北省重点实验室,武汉 430068）

1 引言

当前机械零部件制造的生产效率得到了很大的提升，但随之而来的是大量的机械零部件需要被检测。传统的二维测量设备已不能满足日趋智能化、微型化、复杂化的生产需求，光学三维测量设备应运而生。条纹投影三维测量轮廓术因具有操作简单、适应性强、精度高和非接触测量等优点，已在机电产品质量检测、医疗诊断和模具设计等领域得到广泛的应用[1-6]。但工业零部件的表面通常具有高反光的特性，易造成相机采集的图像出现过饱和现象，导致检测失效[7]。因此，研究具有高亮、类镜面、含局部镜面反射的混合表面等反射率较高的高反光表面的三维面形测量技术具有重要的科学探索意义和实际应用价值。

为实现高反光物体的三维面形测量，国内外学者对多种方法进行深入研究，主要包括多重曝光法[8-9]、硬件附加法[10-11]和自适应条纹投影法[12-17]。其中，多重曝光法常用于高反光物体的视觉成像，但它需要对同一场景采集多幅不同亮度的图像，但被测物体运动或者相机抖动都会导致图像融合时出现重叠的伪影，因此该方法难以应用于复杂多变的工业现场。硬件附加法则是通过改变偏振滤光片透射轴之间的角度来有效的去除高光，但难以消除大多数金属表面存在的镜面反射分量，对高亮的物体表面去高光效果不佳。自适应条纹投影法也是去高光的常用手段，它是基于自适应调整条纹投影强度和反投影的思想上提出的。对于条纹投影测量系统，在建立相机和投影仪的映射关系后，通过改变投影图像灰度可以使相机获取最佳的投影条纹图案[18]。Zhang 等提出一种只需采集具有单次曝光时间的条纹图像以自适应确定全局最佳灰度值，但它需要在固定场景下预先校准相机对不同反射率物体的响应函数，场景较为单一且准备工作耗时较长[19]。Riviere 等基于偏振滤光片技术极大地降低了投影仪的输出光强度和相机的入射光强，但该方法对于暗场景区域很难测量[20]。Wei 等通过一种基于不同强度条纹图案融合的技术，根据最大信噪比将不饱和数据进行组合，从而使全局不出现过饱和情况，精度较高，但这种方法仍需要采集大量图像，且不适用于过亮表面[21]。Chen 等通过被测物体表面的反射特性，运用多项式拟合出每个过饱和区域的最优投射光强值，但当该过饱和区域中饱和像素对应的表面区域反射率变化较大时，函数拟合并不准确[22]。

前述方法中，或者操作过程耗时，或者投影强度计算结果不精确，只适用于特殊场景。针对已有方法的局限性，本文建立一种基于被测表面反射率变化的强度响应关系，提出基于逐像素调制的自适应条纹生成方法，生成并用于高反光表面的三维测量。采用在低光照强度下进行坐标匹配数据，本方法能够根据被测表面的反射率变化逐像素地求取最佳的投影灰度值，生成投影仪坐标系下自适应条纹投影图。实验表明，本文方法拟合速度快，匹配精度高，能够逐像素高精度地调制高反光表面的过饱和区域的投影光栅强度，且适用于大多数金属物体表面，有效提高具有高反射表面特性物体的三维重建精度和适用范围。

2 基本原理

2.1 自适应条纹投影技术

本文提出的自适应条纹投影的三维测量方法的总体流程如图1 所示。首先，通过采集投射至被测表面的最大投影强度为Imax灰度图来判别过饱和像素点。投影横、纵双向条纹进行坐标匹配，并建立相机-投影仪强度关系式以求解像素点的最佳投影灰度值。同时，对相机和测量系统分别进行标定。最后，将生成的自适应条纹投影至被测表面，通过多频外差相移法解算相位以获取高精度的深度信息，并结合已建立的绝对相位与深度信息之间的关系，即可实现对高反光表面的三维重建。

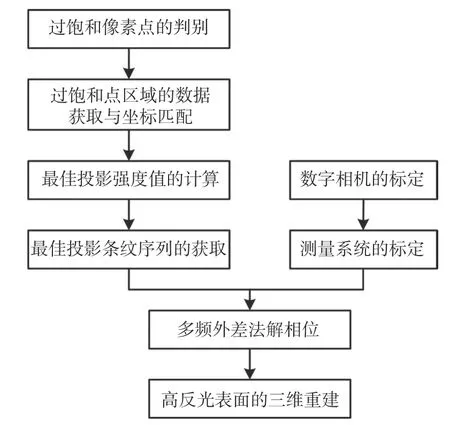
图1 自适应条纹三维测量方法流程图Fig.1 Flow chart of adaptive fringe 3D measurement method

2.2 相机与投影仪间的坐标匹配

在基于条纹投影的三维重建系统中，相机-投影仪的匹配关系如图2 所示。其中(OW;XW,YW,ZW)为 世界 坐标系，(OC;XC,YC,ZC)和 (UC,VC)为相机坐标系及其像平面坐标系，(OP;XP,YP,ZP)和(UP,VP)分别表示投影仪坐标系及其像平面坐标系。在世界坐标系上，任意一点Pw(xw,yw,zw)对应投影仪像平面坐标系上一点Pp(up,vp) 和相机像平面坐标系上一点Pc(uc,vc)。由于Pp和Pc两点具有相同的相位值，通过垂直和水平的相移条纹序列可建立Pp和Pc两点的匹配关系，即可确定相机和投影仪的对应关系。

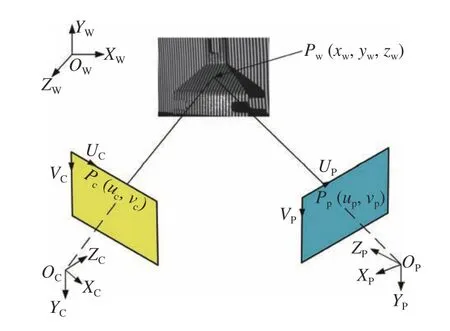
图2 测量系统的坐标系示意图Fig.2 Schematic diagram of coordinate of measurement system

当投影仪向物体表面投射N幅正弦条纹序列时，投射的正弦条纹图案输入强度可表示为：

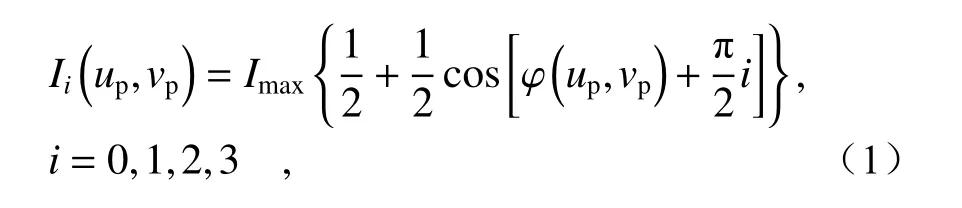
其中，(up,vp) 为投影仪像平面上的任一点坐标，Imax为最大投影强度。通过相机采集的变形条纹Ii(uc,vc)可计算出包裹相位的主值φ(uc,vc)：

其中，(uc,vc)为相机坐标系任一点的像素点坐标，Ii(uc,vc)表示第i次获得的条纹图，φ(uc,vc)为[0,2π]的同余相位值模。相应的绝对相位可通过多频外差相移法从包裹的相位中解算。

相机坐标系下，任一点Pc(uc,vc)的绝对相位可沿着垂直和水平方向分别进行线性插值计算，分别记为φv(uc,vc) 和φh(uc,vc)，则其对应的投影仪像平面坐标系上的像素点坐标(up,vp) 可表示为：

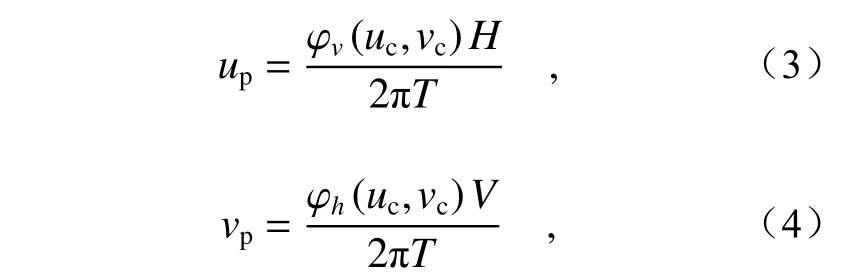
其中，V和H是投影条纹图宽度和高度，T是条纹的最大周期整数。

2.3 最佳投影条纹序列的计算

利用条纹投影系统进行高反光物体的三维重建时，若直接向物体表面投射高亮度条纹图，则在高反射率区域会出现过饱和现象，容易致使该过饱和区域的相位丢失；若投射低亮度的条纹图案至物体表面，则在低反射区域会降低信噪比。因此，只有使该投影条纹图都不会出现过饱和现象，且又能很好地保持低反射区域的调制度，才是最佳的投影灰度值。

对于一个具有未知表面反射率的任意物体，在环境光和复杂表面结构的影响下，很难自适应确定投影条纹图的最佳强度。因此，本文首先估计物体的表面反射率、环境光和表面结构相互作用产生的反射光。为解决此问题，需要确定从相机到投影仪的坐标映射和相机响应函数。在这里，“自适应”是指根据物体表面反射率的变化、环境光和表面结构之间的影响，预测投射至不同反射率和环境光表面上的投影条纹图案的最佳强度。

2.3.1 条纹投影图案中最佳投影灰度值的计算

为确定相机捕获强度与投影仪输出强度之间的关系，有必要了解相机像素点采集到的光强组成。对于相机采集光强，被测表面可以对投射光产生各种影响，包括漫反射、镜面反射、透射光和被测表面的吸收等。对于相机像素点接收的光强可以分为：相应点反射光、其他点的反射光、环境光等，于是相机像素点采集光强Ic可表述为：

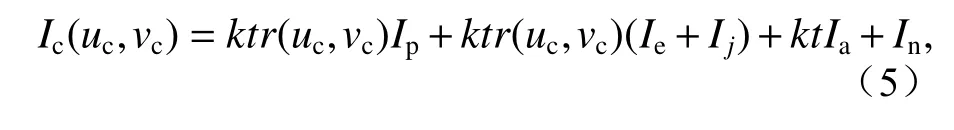
其中，k为相机敏感系数，t为相机曝光时间，r为像素点表面反射率，Ip为投影仪投射光强，Ie为反射的环境光,Ij为反射其它表面的反射光，Ia为直接入射的环境光，In为噪声系数。被测表面的反射光的组成如图3（彩图见期刊电子版）所示。

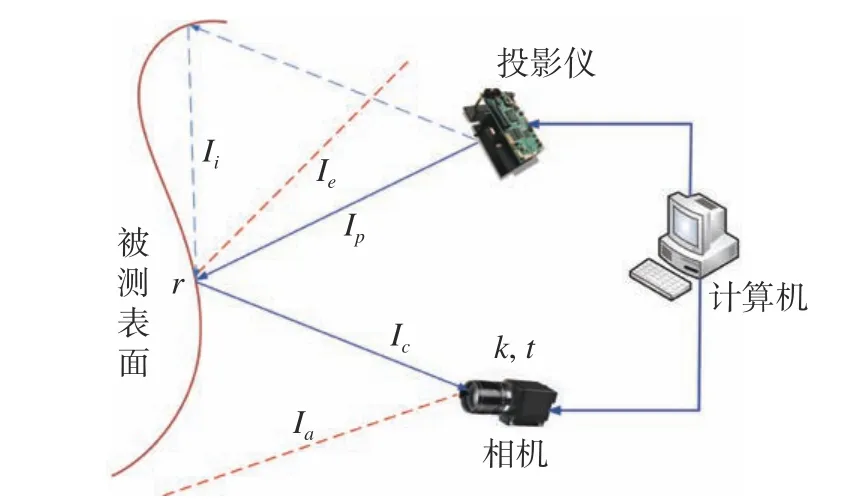
图3 被测表面反射光的组成Fig.3 Composition of reflected light from the measured surface

对于被测表面的物点不仅被使用的光源、环境光照亮，还会被场景中其他光点照亮。而对于其他点的反射光Ij可分为第二反射光和高阶分量光。

其中，M、N表示投影仪的分辨率，h(uc,vc;up,vp) 为从投影仪到相机的光传输系数，是一个二维矩阵，表示整个投影仪像素平面除相机-投影仪匹配点外，其他点对该相机像素点的光强影响。将公式(7)代入公式(5)可得：

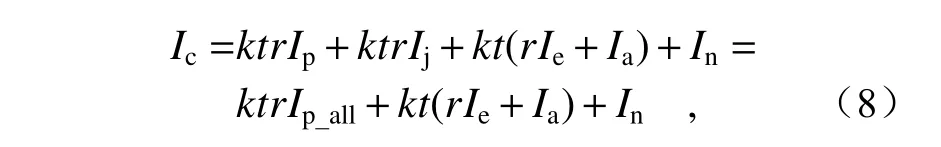
其中，Ip_all表示从数字相机采集投影仪光强的入射光总量。

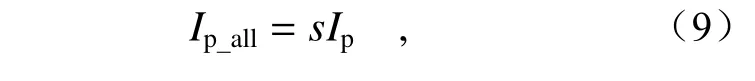
s为采集光强与投射光强系数。设相机采集投影仪入射光的像素内表面反射率为r1，环境光和表面互反射影响系数为r2，则相机响应函数可以表示为：

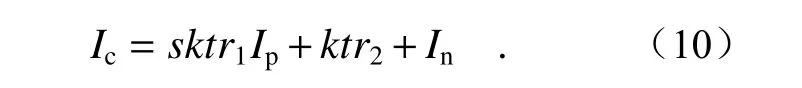
由此可见，在环境光和相机敏感系数、曝光时间不变的情况下，相机捕获光强依赖于投影仪光强和环境光强，将这些不变量与r1、r2结合可设为:

则可建立如下二元一次方程组：

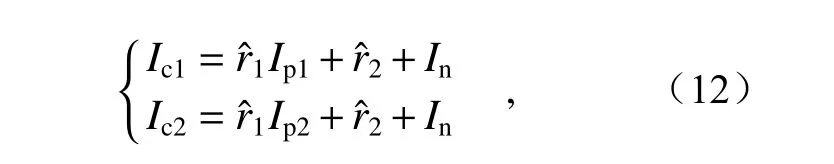
进一步求解得：

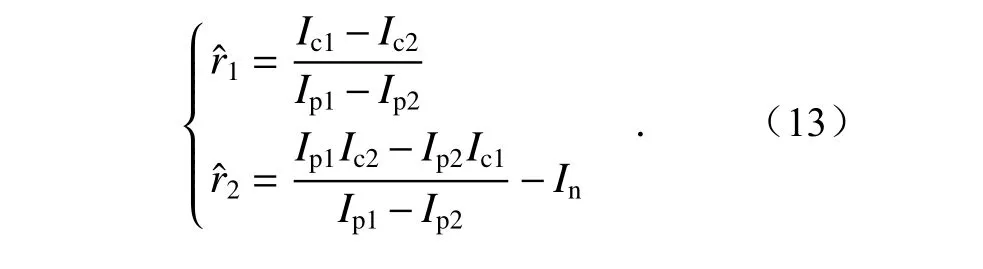
对于投影灰度值Ip的求取，可以通过相机逆响应函数得到。由公式(10)和(11)，可以得到

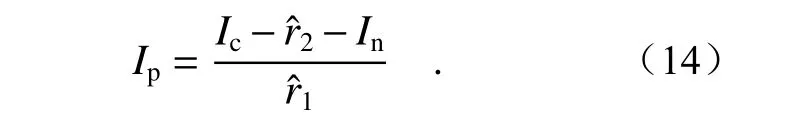
一般情况下，当相机采集到的像素点强度值等于且不超过相机所能采集的最大光强时，即为投影仪的最佳投影灰度值Iopt，表达式为：

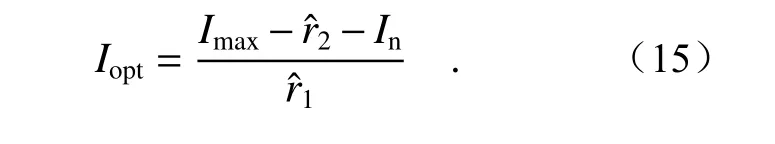
2.3.2 自适应条纹图的生成

本文提出的求取最佳投影灰度值获取的具体方法步骤如下：

Step 1：过饱和像素点的判别。采集投射的灰度图Imax(uc,vc)，若其灰度值大于阈值Tb时，则像素视为饱和，并设该饱和像素点为第m(m=1,···,M)个饱和像素点，其中M为过饱和点的总数，Tb与设备自身产生的噪声和环境光有关。在公式(16) 中，Mc(uc,vc) 是二进制矩阵，当像素点视为饱和时，该二进制矩阵等于1。

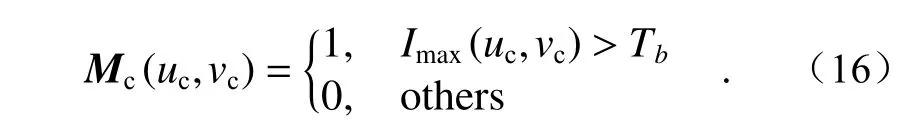
Step 2：过饱和点区域的数据获取与坐标匹配。在低灰度模式下进行相机-投影仪坐标匹配，投射一组最大灰度值为η×Imax的横纵正弦条纹序列Ii(up,vp)，η为调制系数，目的是使相机采集的图像序列Ii(uc,vc)全局不产生过饱和现象。由式(3)、式(4)进行坐标匹配计算。

Step 3：最佳投影强度值的计算。设饱和像素点投影灰度值为xi,m=Ii,m(up,vp)，相机采集到的灰度值为f(xi,m)=Ii,m(uc,vc)，则可根据公式(13)建立求取系数值和为：

Step 4：最佳投影条纹序列的获取。根据式(3)、式(4)中的像素对应关系可知，相机与投影仪中的坐标点一一对应，但由于两者的分辨率不同，坐标映射时会出现多对一的情况。因此，根据相机与投影仪分辨率的比例对应关系，本文将相机坐标系中的点Pc(uc,vc) 与对应投影仪坐标系下的点Pp(up,vp) 及其周围4 邻域的坐标范围相对应，即调整Pp点的灰度值意味着点Pp及其周围4 邻域区域的灰度值均有调整，如图4 所示。建立相机-投影仪坐标系的对应关系后，再将计算得到的投影仪坐标系下点Pp的最佳投影灰度值与标准正弦条纹相结合，即可得到最佳的投影条纹序列。

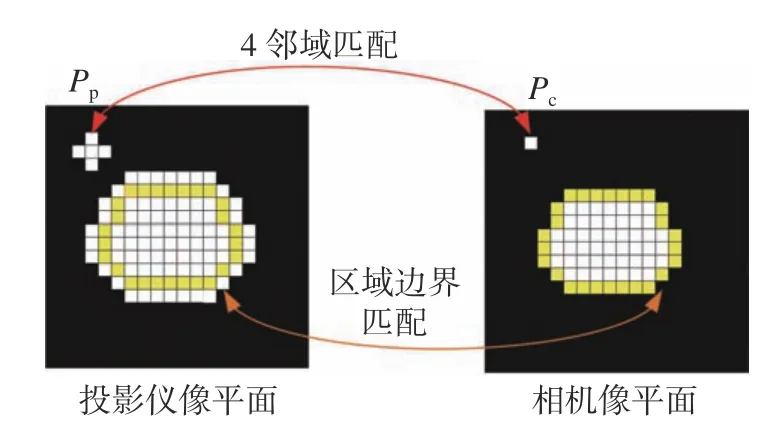
图4 4 邻域匹配法Fig.4 Matching method based on 4 neighborhoods

3 实验分析

3.1 硬件搭建与相位展开

自主搭建了一套自适应条纹投影的三维重建系统，实验平台如图5 所示。该系统主要由数字相机、数字投影仪、校正板、支撑件、服务器和被检测零件构成。数字投影仪型号为DLP4500，可实现RGB 三通道图案的高速投影，有效分辨率为1 140 pixel×912 pixel。数字相机型号为Grasshopper GS3-U3-32S4M，最大分辨率为2 048 pixel×1 536 pixel，其最大帧频可达到121 frame/s。

图5 三维测量系统实验平台Fig.5 Experimental platform of 3D measurement system

实验过程中选取具有局部反射率较大的机械零部件为实验对象。

首先，对相机-投影仪测量系统进行校正。固定相机和投影仪位置，使相机与投影仪成一定锐角。根据张正友标定法，多次移动标定板的位置和方向，对相机的内外参数进行标定，建立绝对相位信息和物体高度的关系[23]。

结合实验室环境光的影响，向被测物体表面投射一幅最大投影强度Imax=255 的灰度图，相机采集的实际场景如图6(a)所示，可见图像中有部分区域存在过饱和现象，获取图像中饱和像素点的位置。将相机光圈调至合适大小，以尽量减小环境光照对实验的影响，且相机曝光时间设置为1/fp的整数倍，其中fp为投影仪的刷新帧率。因考虑到实验过程中设备产生噪声和环境光照的影响，设置饱和阈值Tb=250。根据公式(16)，即可计算出阈值分割后的图像，如图6(b)所示。

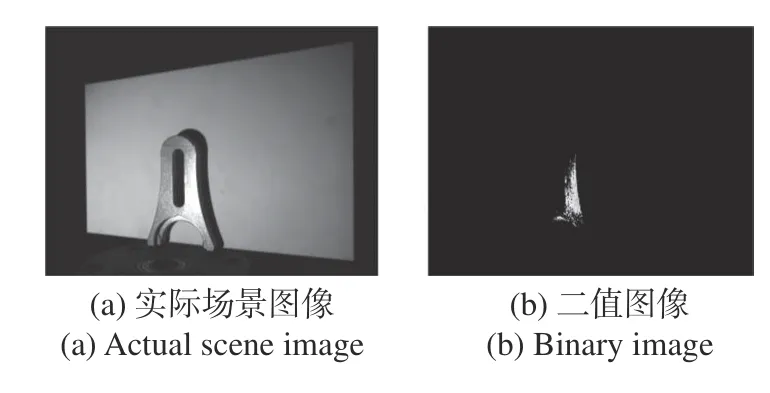
图6 阈值分割效果图Fig.6 Threshold segmentation graph

结合Step 1 中的物体表面过饱和信息，预估计并调整使实验中的η=0.5，使物体表面不产生过饱和现象，在调制模式下实现过饱和区域的相机-投影仪坐标匹配。向被测表面投射一组最大灰度值为120，最佳条纹个数分别为70、64、59 的横纵条纹图，利用多频外差四步相移法进行相位解算，其对应的相位主值分别为Ф1、Ф2、Ф3。再通过外差法计算叠加相位Ф12、Ф23，最后将Ф12、Ф23的相位叠加到全场范围内只有一个周期的相位Ф123，实现流程图如图7所示。

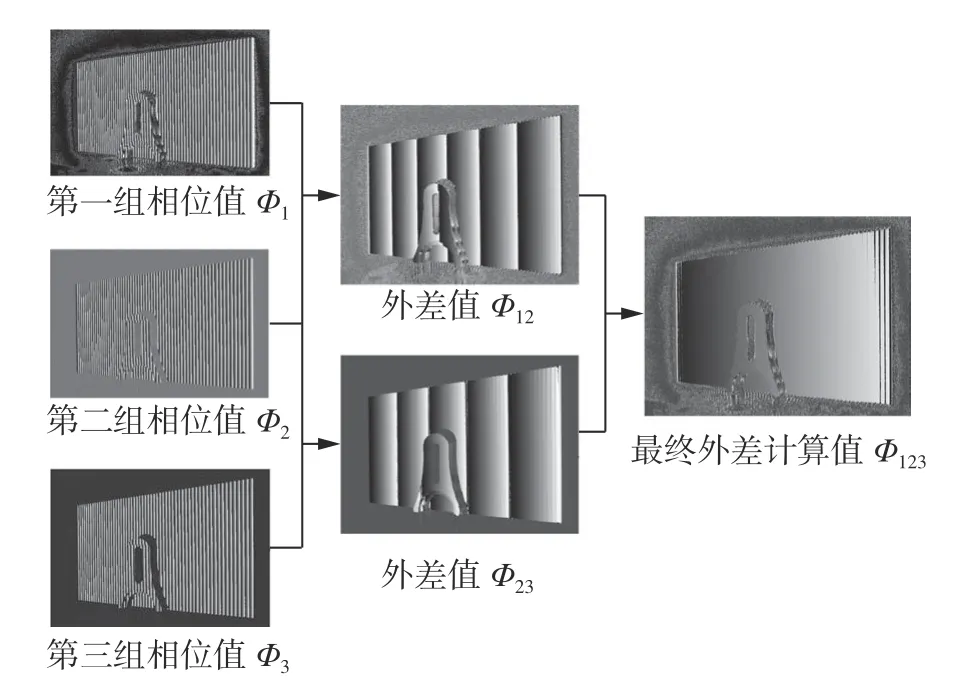
图7 相位展开流程图Fig.7 Flow chart of phase unwrapping

根据式(3)、式(4)和Step 5 可求解相机坐标系下的过饱和点的最佳投影值，再结合最大投影灰度为Imax的标准正弦条纹，可得到投影仪坐标系下的最佳投影条纹，如图8(a)所示，整个自适应条纹图的生成过程仅需要一幅最大灰度值的灰度图和一组24 幅低灰度下的横纵条纹图。随后，采集投影至物体表面的实际条纹，如图8(b)所示。最后，通过多频外差四步相移法求解实际采集条纹的绝对相位，并结合相位与高度的关系，即可重建出物体的三维面形。

图8 自适应投影条纹图Fig.8 Adaptive projection fringe image

3.2 对比实验及适用性分析

针对本文方法的适用范围，分别对具有类镜面、高亮、混合表面以及其他无规则散射等反射率较高的物体表面和具有一定曲率的高反光物体进行三维重建分析，运用传统的光栅投影三维测量方法[24]与本文所提的方法对类镜面的鼠标表面、具有高反光特性的金属工件叉板、圆柱曲面和精密加工的抛光磨具进行三维重建，实验结果对比如图9（彩图见期刊电子版）所示。从图9（a）红色矩形区域可看出，经传统光栅投影三维测量方法得到的被测表面的三维点云及其拟合模型中均存在明显的局部点云缺失现象。图9（b）是运用本文方法获得的被测表面三维点云及其拟合模型，可见三维模型中点云无明显缺失。实验中，多组不同类型的被测对象充分证明了本文方法的有效性和适应性。由此可知，采用本文提出的方法对含有局部镜面反射区域的高反光被测物体表面的三维面形可被完整重构，且适用于大多数具有一定曲率特性的物体表面。

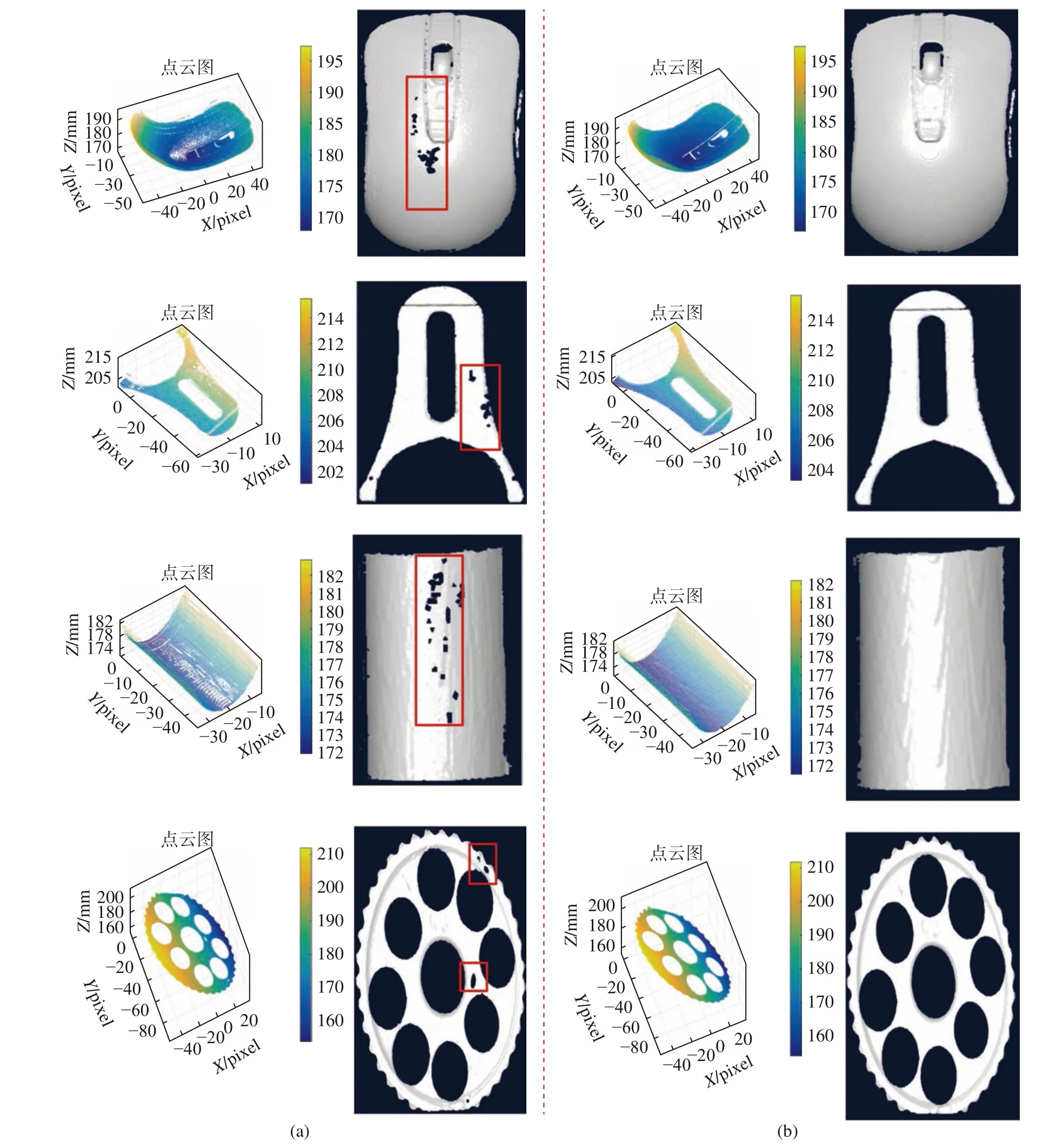
图9 （a）传统方法及（b）本文方法三维重建结果Fig.9 3D reconstruction results obtained by (a) traditional method and (b) the proposed method

4 误差分析

为评估本文方法的性能，对同一基准平行平面的物体进行三维测量，并对物体的点云数据进行计算，以客观评价测量方法的精度误差。经实际测量物体高度值为20.00 mm，分别运用传统方法[24]和文献[21]、[22]中Wei、Chen 的测量方法与本文方法，对该平行板工件的原始点云数据进行质量分析，重建效果如图10（彩图见期刊电子版）所示。

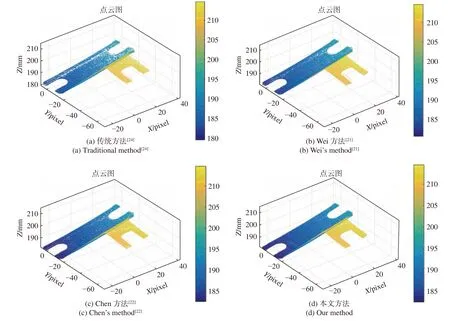
图10 不同方法的三维重建结果Fig.10 Experimental results of 3D reconstruction with different methods

对于上述同一测量对象，不同测量方法的误差检测结果见表1。对采集图像的过饱和像素点数进行了统计，以补偿过饱和区域的有效补偿率和点云坐标的均方根误差作为评价标准，其中均方根误差的值越小表示测量结果的精度越高，其表达式为：

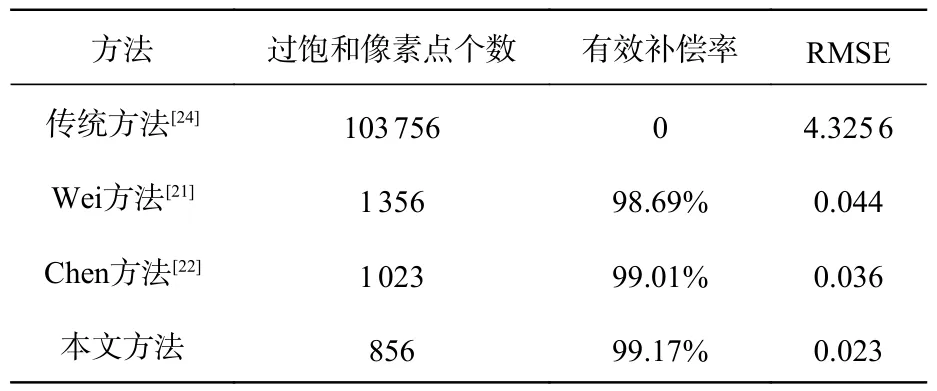
表1 本文方法与现有方法的误差检测结果Tab.1 Comparison of error detection results between the proposed method and existing methods

其中，n为重建物体像素点总数，Pcap,i为重建的第i个像素点云坐标，Pmodel,i为三维模型的第i个点云坐标。

依据最小二乘法拟合平面并计算两平面点的距离均值、平均误差与标准偏差，以定量评价所提方法的有效性，结果见表2。规定超过物体高度值为正向偏差，小于物体高度值为反向偏差。

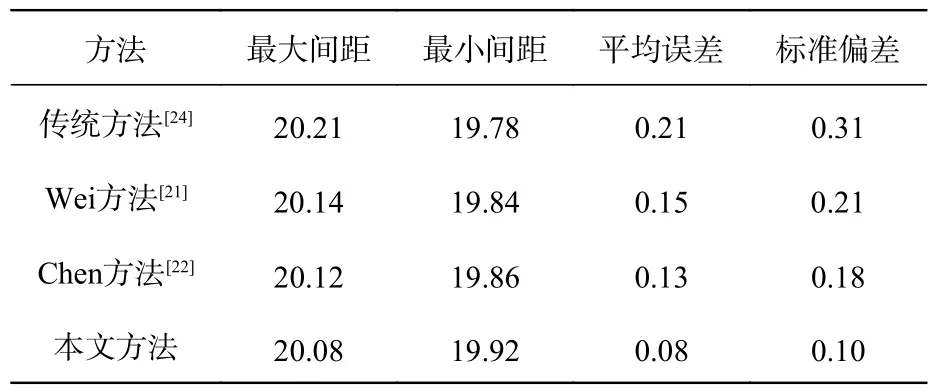
表2 本文方法与现有方法的误差对比分析Tab.2 Error analysis comparison between the proposed method and existing methods (mm)

由表1 和表2 定量分析可知，本文所提方法对过饱和像素点的补偿率可达到99%以上，且其均方根误差、间距平均误差和标准偏差均小于其他方法所得的测量值，其中，平均误差与Wei、Chen 方法对比分别减小47% 和38%，标准偏差减小52%和44.4%。与传统方法相比，平均误差减少61.9%，正向误差减少61%，反向误差减少63.6%，标准偏差减少67.7%。因此，相比于其他方法重建出的三维物体，本文所提方法对高反光物体的三维重建精度显著提高。

5 结论

针对高反光表面的三维测量难题，本文提出了一种可根据被测物体表面反射率逐像素调制的自适应条纹投影方法，有效解决因被测表面的过度曝光、相位获取不完整而导致三维重建过程中点云信息缺失的问题。实验结果表明，本文方法可以有效重建出高反光表面的三维面形结构，获取完整的点云信息。本文所提方法不需要大量采集不同灰度值的投影灰度图像序列，且不用对硬件设备进行改动，方法及原理新颖，操作简便，且精度较高。实际测量误差约为0.08 mm，均小于文中其他方法所得的测量值，相对传统方法平均误差减少61.9%，标准偏差减少67.7%。但本文方法在实际测量过程中会受到噪声的影响，后期将深入研究去噪算法以减少外界环境的影响。