微细正交切削过程原位观测中位移补偿方法

张向辉，于化东,2，许金凯，于占江，李一全，于浩洋

（1.长春理工大学 跨尺度微纳制造教育部重点实验室,吉林 长春 130022；2.吉林大学 机械与航空航天工程学院,吉林 长春 130025）

1 引言

微细切削已经成为金属材料微小零件制造的一种常用且重要的工艺方法，微细切削主要指采用为几十微米至几微米的切削厚度进行切削，其具有良好的适用性，在多种复杂结构微小零件的制造过程中用于实现关键加工工序。

对于微细切削的研究主要包括两个方面：1.切削参数对微细切削过程的影响；2.微细切削机理的研究。

对于切削参数对微细切削过程的影响，选取切削深度、进给速度、主轴转速以及刀具的尺寸作为分析参数，通过微细切削实验以及响应曲面数据分析法得到切削参数对表面加工质量的影响规律，从而优化加工参数以得到良好的加工效果，获得高的表面加工质量[1]。

在微细切削机理研究方面，进行的工作多是理论模型推导，主要集中在切削力模型的建立及验证，对于切削过程中金属材料的位移以及变形大部分还是通过有限元法进行仿真计算[1]。在微细切削的机理研究中，针对刀具工件的相对位移以及金属材料的变形直观分析已成为研究微细切削机理的关键。

原位成像和数字图像相关分析技术（Digital Image Correlation，DIC），是分析固体变形和应变常用的光学实验技术。由于DIC 相应测量分析算法的健壮性，以及其非接触检测的特性，目前被广泛用于检测金属材料在拉伸断裂以及挤压弯曲变形过程中产生的塑性位移以及形变，并取得了良好效果[2-7]。随着成像技术的发展，原位成像和DIC 分析技术也被用于金属材料切削时位移场和形变场的原位测量分析，并且获得良好的测量精度[8-9]。相对于常规切削，微细切削的切削厚度在几十微米至几微米之间，要想对其过程进行清晰记录必须使用显微镜筒和显微物镜，相应的微米级别原位测量方法正是基于此原理进行开展的[10-11]。同时，由于显微镜筒和显微物镜具有放大作用，外界振动对测量结果产生的影响就不能被忽视。为了能够采集大行程的微细切削图像信息，通常采用刀具和高速相机静止，工件运动的切削方式，这就导致数字图像相关性分析得到的计算结果受到切削进给速度的影响，无法清晰体现微细切削过程中工件材料位移场的分布情况，从而使工件材料在刀具切削作用下的运动趋势分析变得困难。

针对上述问题，本文提出改进型图像模板匹配算法，对切削过程中由外界振动和工件进给运动在原位观测图像序列中引入的位移偏差进行补偿，在保证匹配精度的同时解决了常用图像模板匹配算法计算效率低耗时长的问题，大幅度提高了匹配计算效率，缩短了匹配搜索耗时。基于所提改进型图像模板匹配算法在后续变形区DIC 位移场分析中增加位移补偿环节，可以将工件材料变形参考区转为静止状态，使得变形区位移场分析结果中工件材料在刀具作用下的相对运动趋势更直观清晰。

2 DIC 分析原理

2.1 实验条件

本文针对材料牌号为H70 的黄铜的微细正交切削过程进行原位观测分析。为观测记录H70 黄铜微细正交切削过程，搭建如图1 所示的观测系统。

图1 微细正交切削观测系统Fig.1 Micro orthogonal cutting observation system

观测系统包括：高速相机、显微镜筒、显微物镜、照明光源、多自由度调整平台。高速相机的最大帧频为2 000 frame/s，分辨率为2 000×2 000，单像元尺寸为11 μm。为尽量减小切削过程中的振动对观测产生的影响，高速相机外置固定在机床外部的多自由度调整平台上。显微镜筒的放大倍数为3 倍，显微物镜的放大倍数为10 倍，整个观测系统的总体放大倍数为30 倍，单像元尺寸经过显微镜筒和显微物镜放大后变为0.336 7 μm。为了能够清晰观测H70 黄铜在微细正交切削过程中的材料变形，以及切屑的形成，实验采用外置光和同轴光两组光源照射。同轴光用于相机对焦，外置光源通过光纤加聚焦透镜分为4 个光束均匀照射工件和刀具表面，所搭建的微细正交切削观测系统相关坐标系及观测到的工件和刀具图像如图2 所示。其中，机床的X轴运动方向与图像列方向对应，二者正方向相同，Z轴运动方向与图像的行方向对应，二者正方向相反。

图2 （a）微细正交切削观测系统相关坐标系；（b）显微观测成像Fig.2 (a) Corresponding coordinate system of micro orthogonal cutting observation system;(b) microscopic observation imaging

2.2 微细正交切削DIC 位移场分析

为进行DIC 分析，需要对观测物体表面进行处理得到散斑图，本文通过飞切和表面腐蚀的方式对工件表面进行加工处理，图2（b）为相应散斑图。

如图3 所示，设定数域或图像域 Ω ⊂Rn，经历变形y:Ω !Rn,(n=2,3)，用X表示散斑图中参考粒子或未变形粒子在图像域Ω 内的位置，用y(X)表示已变形粒子的当前位置，如图3 所示。

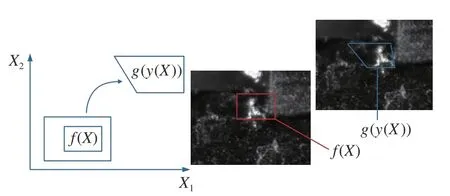
图3 变形前后图像之间的区域对应Fig.3 Region correspondence between images before and after deformation

假设在参考域内有一散斑图案对应的灰度值为f(X),在当前变形后图像域内对应的灰度等级值为ɡ(y)。如果变形与灰度等级相对应，就有以下关系式：

数字图像相关性分析要解决的问题是针对给定的变形前后图像f(X)和ɡ(y)寻找相对应的变形y(X)。亦可以将其称为一个优化过程，或者寻找一个变形映射的过程，使式（2）中的平方差最小。

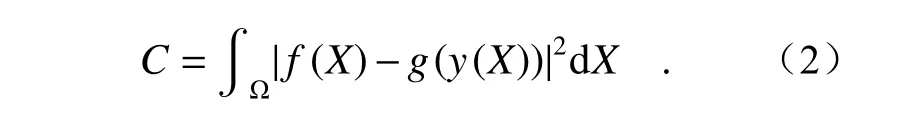
对于上述过程需要注意以下几点：（1）数字图像相关性分析所针对的图像是像素化的，因此上述中的f和ɡ取离散值，可以用求和来代替式（2）中的积分运算，同时为提高计算结果的精度可以对图像进行插值处理；（2）由于在实验过程中会存在照明伪影和增益误差，对图像进行归一化处理来消除二者对计算结果的影响是很有必要的。图像归一化处理方法的依据是使变形前后的图像具有相同的均值和标准差，如式（3）所示。

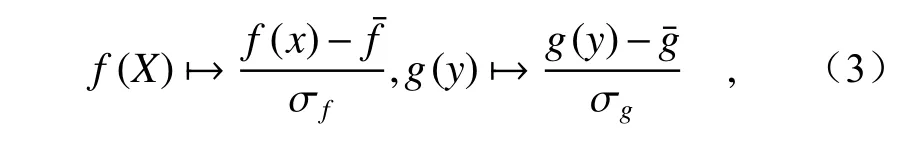
3 改进方法

由上述DIC 的相关原理可知通过DIC 可以对切削区域的位移场分布进行分析，同时也可知工件移动会对位移场计算结果引入位移偏差，造成工件变形区材料间的相对运动趋势不再明显。本文为解决此问题，在进行DIC 分析前，增加一个位移补偿环节，分为两个工作步骤：（1）图像序列间相对位移检测；（2）图像序列间位移补偿。

3.1 DIC 分析图像序列间的位移检测

3.1.1 数字图像模板匹配算法

本文使用数字图像模板匹配算法对图像序列间切削工件的相对位移进行检测，常用的模板匹配算法有：平均绝对差算法（Mean Absolute Differences，MAD）；绝对误差算法（Sum of Absolute Differences,SAD）；误差平方和算法（Sum of Squared Differences,SSD）；平均误差平方和算法（Mean Square Differences，MSD）。这些算法的优点是运算过程简单，匹配精度高，但是，运算量偏大，且容易受到图像噪声的影响[13-14]。为降低图像噪声的影响，提高算法的稳定性，本文使用归一化积相关模板匹配算法（Normalized Cross Correlation，NCC）进行检测，基本原理是针对搜索图像和模板图像的灰度，通过归一化相关性度量公式计算二者间的匹配程度，其表达式如式（4）所示，对应的图像全局区域搜索匹配流程如图4 所示。

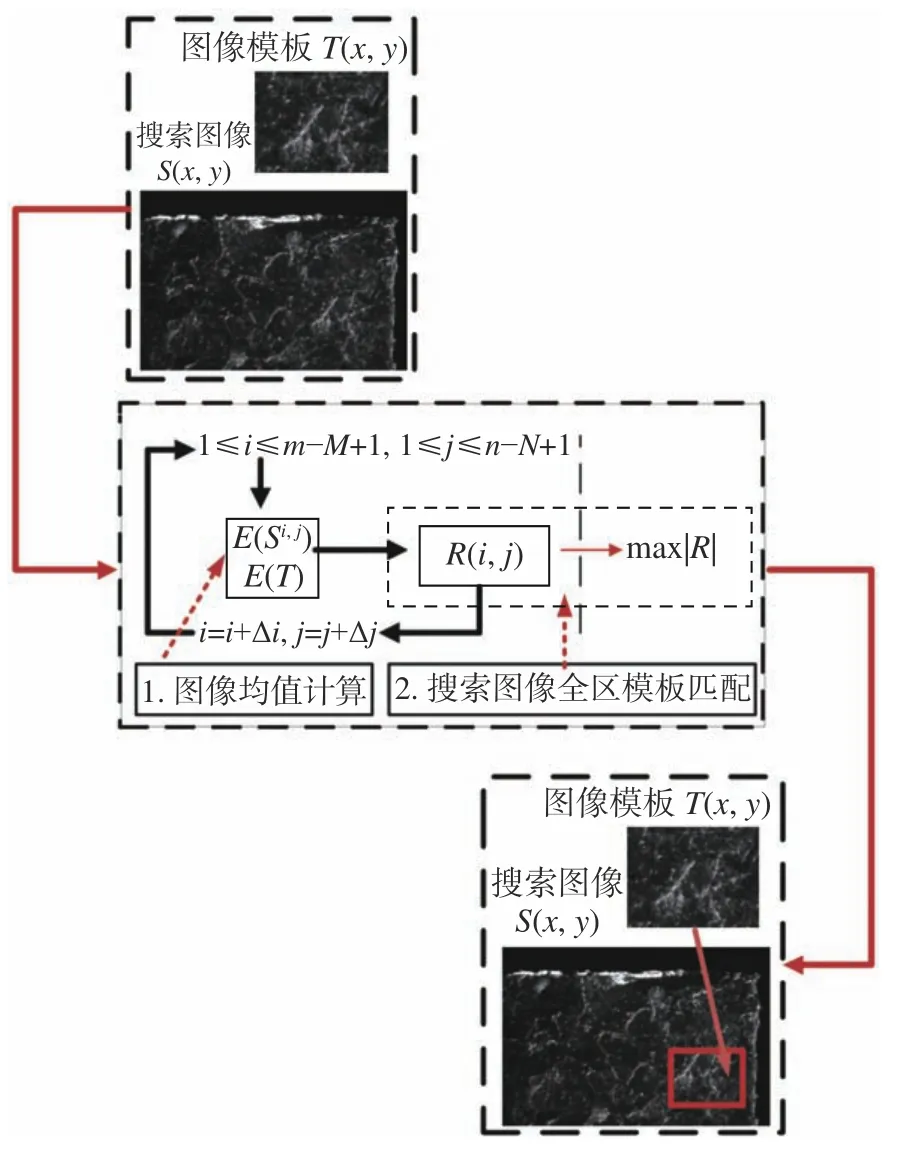
图4 数字图像归一化积相关模板全局匹配流程图Fig.4 Flow chart of global template matching of digital image normalized cross correlation

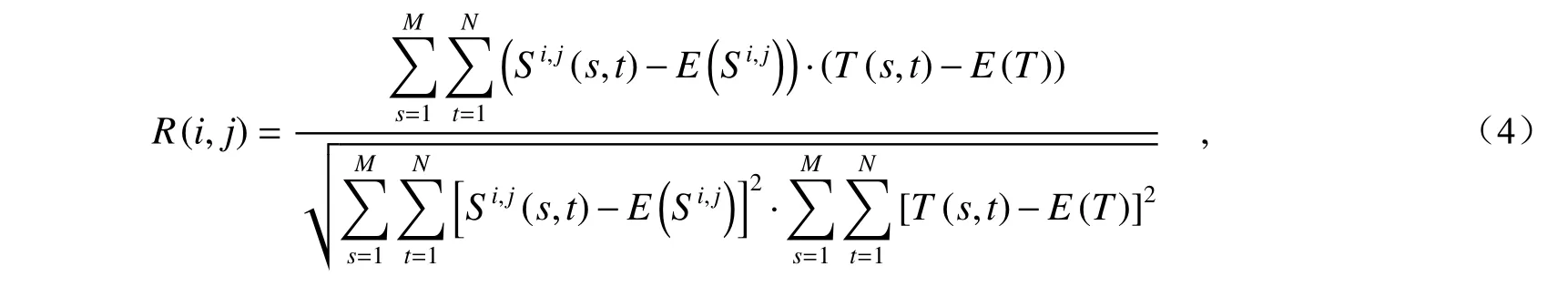
式中，E(Si,j)，E(T)分别为子搜索图像Si,j(s,t)和模板图像T(s,t)的均值。在搜索图像的图像域内，以第(i,j)个像元作为子图像匹配域的左上角，截取大小为M×N的子匹配图像Si,j(s,t)进行相似度计算，得到子图像匹配域与模板图像之间的相关性度量值R(i,j)。其中像元索引序号i,j的取值范围为 1 ≤i≤m−M+1,1≤j≤n−N+1。

3.1.2 添加位移约束的尺寸压缩匹配算法改进

上述流程图4 中，在搜索图像域截取子图像匹配域时，匹配结果的精度与图像行列两个方向上的增量∆i、∆j的取值有关，取值越小匹配结果精度越高，但会导致计算量增大，影响匹配搜索速度。为减小运算量、提高匹配速度，本文基于图像尺寸压缩以及引入运动约束缩小搜索范围的思想对归一化积相关模板匹配算法进行改进，提出二级图像尺寸压缩匹配算法，实现流程包括两个步骤：（1）在变形前图像中截取模板图像，添加运动约束，依此约束在变形后图像中截取搜索图像；（2）使用图像尺寸压缩匹配算法进行图像匹配。

设定截取的模板图像起始点像元（左上角像元）在变形前图像中的位置为(iTS0,jTS0)；正交切削工件运动速度为vc，运动方向为沿机床X轴正方向，即图像的列方向正向；显微镜筒的放大倍数为TS，显微物镜的放大倍数为T0，高速相机采集帧频为fc，高速相机单像元尺寸为PSX=PSY=PS；由于工件的进给运动，在变形后模板图像对应的起始点像元理论位置将变为 (iTS1,jTS1)。则(iTS1,jTS1) 与(iTS0,jTS0)之间的对关系如式（5）所示。通过计算得到模板图像在变形后图像中起始点像素理论位置 (iTS1,jTS1)后，结合所设定的边界扩展值∆BXe、∆BYe,以及模板图像的大小M×N，就可以得到搜索图像在变形后图像中的位置(iSS,jSS)以及大小m×n。根据所得位置、尺寸参数在变形后图像中即可截取搜索图像S(x,y)，对应的流程如图5 所示。

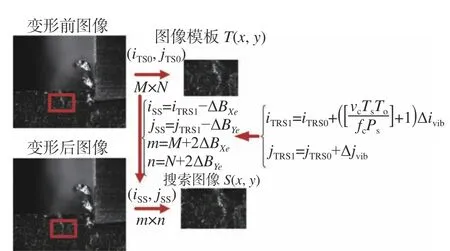
图5 添加运动约束搜索图像截取流程图Fig.5 Flow chart of search image capturing with motion constraint

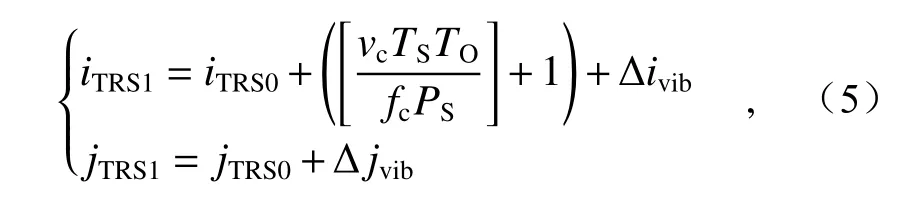
其中，∆ivib、∆jvib为由外界环境中的振动引起的变形前后图像间的位移误差预估值，其值受外界振动和图像放大倍数的影响，这里取值为∆ivib=∆jvib=3；图像列方向上受到工件进给运动的影响，其作用以运动约束形式体现在上式（5）中，对应项为：

在变形后的图像中截取搜索图像后使用压缩比例系数Md对搜索图像和模板图像进行尺寸压缩，其尺寸即上述的m×n、M×N，减小为原图像的1/。图像中原有的灰度特征还会保留。对尺寸压缩后的图像进行搜索匹配，可以大幅度减小计算量，能够快速确定模板图像在搜索图像中所对应的粗略位置(iTR,jTR)。依据压缩比例系数Md和搜索匹配得到的粗略位置(iTR,jTR)，在搜索图像中截取左上角像素位置为(iTRS,jTRS),大小为w×h的二次搜索区域，然后运用归一化积相关模板匹配算法再次进行搜索，得到模板图像在二次搜索区域的精确位置(iTF0,jTF0)，最后通过二次搜索区域在搜索图像中的位置(iTRS,jTRS)以及(iTF0,jTF0)得到模板图像在搜索图像中的精确位置(iTF,jTF)。图像尺寸压缩匹配算法的相关计算及图像处理流程如图6 示。

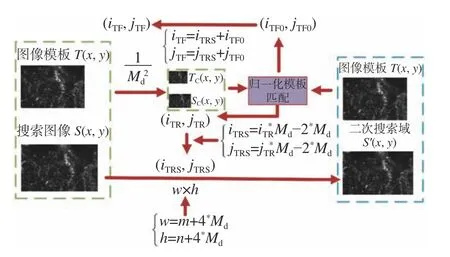
图6 图像尺寸压缩匹配算法流程图Fig.6 Flow chart of the image size compression matching algorithm

3.2 图像序列间位移补偿

由上述改进型图像尺寸压缩匹配算法可以测量出变形前后两张图像IMUdef(x,y)，IMdef(x,y)中由于工件进给运动以及外界振动引入的工件材料的位移量，设定其行列方向上的位移分量为∆iM，∆jM。在后续的DIC 分析中，在变形区的位移场分析结果中引入位移偏差，即∆iM，∆jM。这里通过图像平移变换方法进行补偿，并在位移补偿后的变形前后图像IMMUdef(x,y)、IMMdef(x,y)中截取要进行DIC 分析的子图像IMNUdef(x,y)、IMNdef(x,y)，其处理流程如图7 所示。

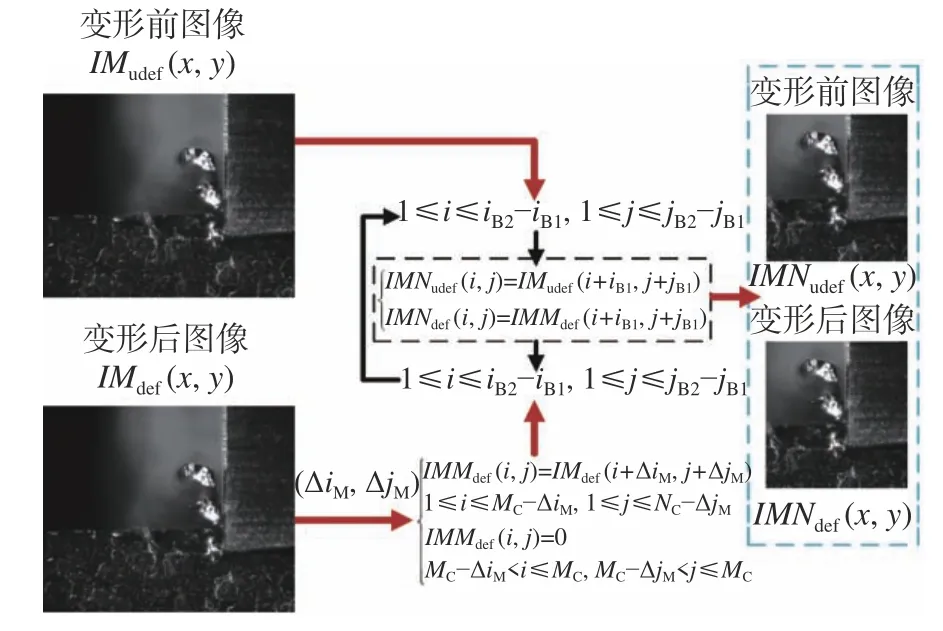
图7 变形前后图像间相对位移的补偿及DIC 分析图像截取Fig.7 Relative displacement compensation between images before and after deformation and interception of the image used in the DIC analysis

上述流程所对应的算法原理如式（6）和式（7）所示。

其中两子式对应的条件为：

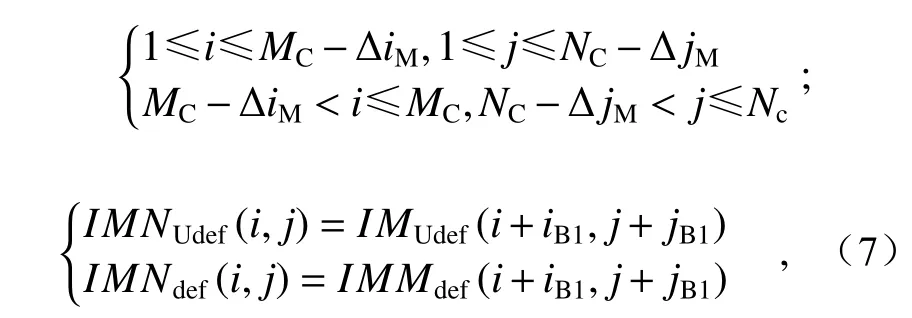
其中两子式对应的条件为：

式（6）和式（7）中，MC、NC为原图像序列中图像的行列尺寸，由采用高速相机分辨率决定，这里取值都为2 000；iB1、iB2为位移补偿后变形前后图像中截取子图像行方向边界值；jB1、jB2为要截取子图像的列方向边界值。

4 实验结果与分析

为验证所提出改进型图像匹配算法的效率和匹配结果的准确性，本文将其与NCC 全局匹配算法进行对比，评价指标为算法运行消耗时间Tp以及模板匹配运算得到的最佳相似系数max|R|。在记录的微细切削过程图像序列中截取的搜索图像和模板图像以及对应的实验参数如图8 所示，其中，所采用的切削参数为切削深度αp=60 μm，工件沿机床X轴正方向（图像列方向正向）切削进给，速度为vc=40 mm/min。所选取的搜索图像为8(b)、8(c)、8(d)、8(e) 与模板图像域(图8(a-I))在图像序列上对应的序列编号NI分别为1，2，3，4，模板图像域同时作为DIC 分析中的变形前图像，即参考图像，所对应图像序列编号NI为0。

图8 (a-Ⅰ) 模板图像和(a-Ⅱ) 匹配搜索图像以及相应实验参数(ap=60 μm,vc=40 mm/min)Fig.8 (a-Ⅰ) Template image and (a-Ⅱ) matching search image and employed experimental parameters

使用NCC 模板匹配算法针对所截取的模板图像，在搜索图像全区域内进行模板匹配搜索，为保证搜索精度，选取图像行列方向上的增量值都为1，即对应算法流程图4 中的∆i=1，∆j=1，所得到的搜索匹配结果及程序运行消耗时间如图9 所示。为更直观地体现搜索匹配算法计算结果的精度，绘制出在搜索图像全区域上的相似系数R(i,j)分布图，如图10 所示。

图9 NCC 模板匹配算法全区域匹配结果及耗时Fig.9 All-region matching results and time consumption obtained with NCC template matching algorithm

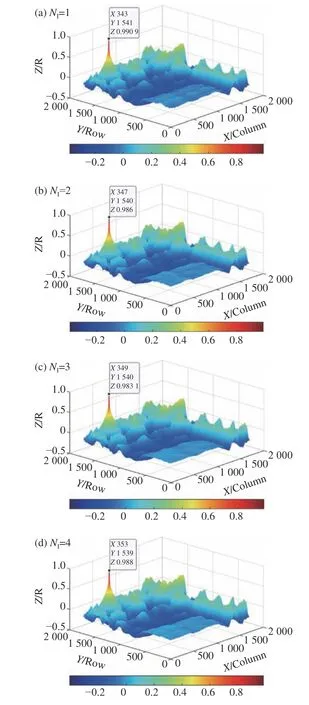
图10 搜索图像全区域相似系数分布图Fig.10 The distribution map of the similarity coefficient in the whole area of the search image

由图9 中对应的搜索匹配结果，可以看出在使用NCC 模板匹配算法在全图像域内进行匹配搜索时，计算量巨大，程序运行消耗时间长，针对图像序列中的4 幅图像进行模板匹配所消耗时间TP在1740.2 s～1875.6 s 之间，得到相似系数R的取值范围为0.983 1～0.990 9。由于受到外界振动和机床运动误差的影响，模板图像在搜索图像序列中的对应位置在图像列方向上（机床X轴运动方向）不是等间隔变化的，同时在图像行方向上（机床Z轴运动方向）的位置存在微小波动。同时，由图10 可以看出使用NCC 模板匹配算法在全图像域内匹配搜索到的位置点处所对应的相似系数R为全图像域上的最大值，且明显高于周围区域的取值。由于该方法搜索范围覆盖全图像域，不存在遗漏的可能，搜索匹配精度最高，因此，选用该算法结果可以评价改进型图像匹配算法匹配精度的参考。

针对图9 中的4 幅图像使用改进型图像匹配算法进行搜索匹配，运行算法程序所消耗时间如图11（彩图见期刊电子版）所示。其中，Md=1 为只引入运动约束的改进算法；Md=2,4 为在引入运动约束的同时使用图像尺寸压缩匹配改进算法，对应的压缩比例系数分别为2 和4。

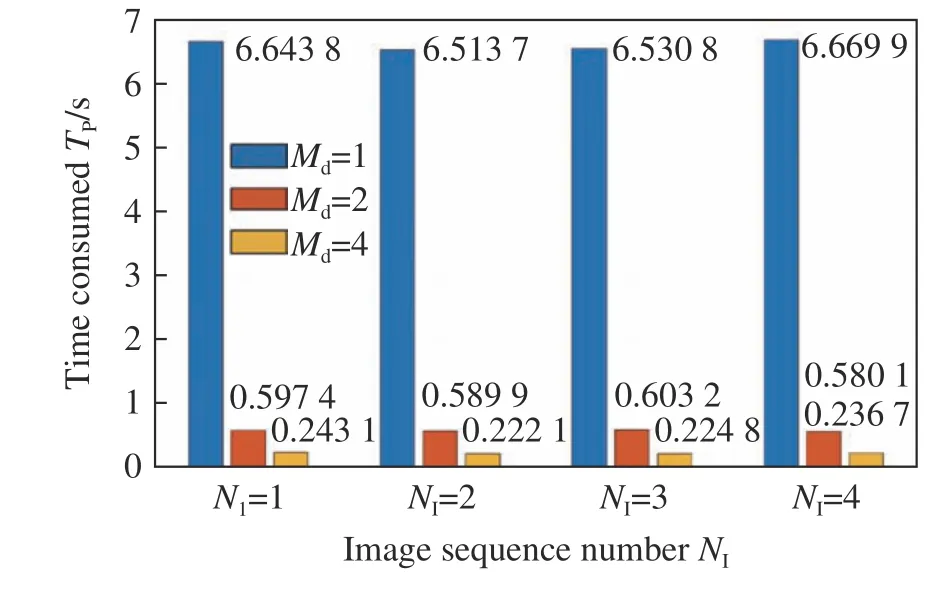
图11 改进匹配搜索算法程序运行消耗时间Fig.11 Time consumption of the improved matching search algorithm

为更加清晰地比较两个算法的运行效率，引入评价参数——相对执行效率Rer，对改进算法的运行效率提升效果进行表征，其计算方法如式（8）所示，对应的各匹配搜索算法之间的相对执行效率计算结果如图12 所示。

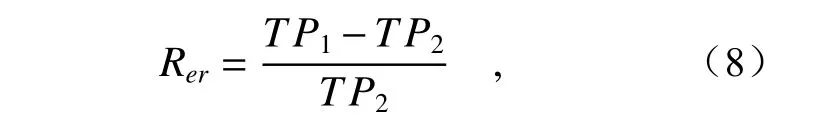
其中，TP1为算法改进前程序运行时间，TP2为算法改进后程序运行时间。

通过对比图11 和图12 中各匹配搜索算法耗时，可以看出在引入运动速度约束后可以大幅减小程序运行时间，提升搜索匹配速度，再通过压缩匹配算法可以更大程度地提升算法的执行效率。在只引入运动速度约束时，即图像压缩比例系数Md=1，相比于NCC 全局匹配搜索算法，本文算法相对执行效率Rer提升至260.9～284.1；在引入运动速度约束的同时使用图像尺寸压缩匹配，对应压缩比例系数为Md分别为2,4 时，其相应算法的相对执行效率Rer分别提升至2 897.2～3 232.2 和7 157.3～8 361.6。至于同一压缩比例下，即Md取值相同时，改进型搜索匹配算法相对执行效率存在差异的原因是由于运行匹配算法的计算机操作系统为非实时操作系统，其抢夺资源式的运行机制会产生随机误差，并且程序耗时越短，相对执行效率的差异越大，但是改进型算法相对执行效率的提升趋势不受影响。

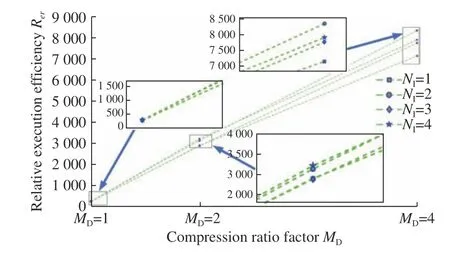
图12 改进匹配搜索算法相对执行效率Fig.12 The relative execution efficiency of the improved matching search algorithm

由上述结果分析可以得出，引入运动约束以及使用图像尺寸压缩匹配的匹配算法可以大幅度提升算法的相对执行效率，其搜索匹配精度为本文所关注的另一个关键点。使用上述改进算法对图9 所示的4 幅图像进行模板搜索匹配，得到的搜索匹配结果如图13 所示。

图13 改进的匹配搜索算法的匹配结果Fig.13 Matching results obtained with the improved matching search algorithm

图13 中，POS0为子搜索图像域在全搜索图像域中的位置，POS1为模板图像在子搜索图像域中的位置，模板图像在全搜索图像域中的位置POS可由式（9）得到：

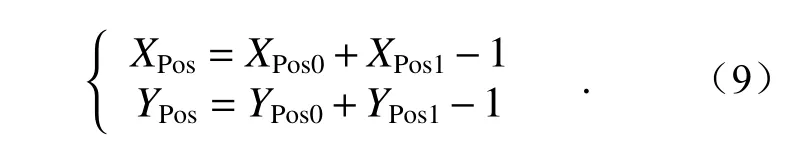
通过对比图13 与图9 中的全搜索图像域中的位置POS以及相似系数R值可以看出：在图像序列中对应图像上使用改进型压缩匹配算法和NCC 全局模板匹配算法可以得到相同精度的搜索匹配结果。由此可知，本文提出的改进型压缩匹配算法在大幅度提升搜索效率的同时还能够保证搜索匹配精度。将上述图13 中模板图像在搜索图像中的位置分别减去图8(a)中模板图像在模板图像域中的位置，就可以求得图像序列间行列方向上的相对位移量，对应3.2 节中的∆iM，∆jM，同时将其换算成机床X、Z坐标轴上的位移量，结果如图14（彩图见期刊电子版）所示。

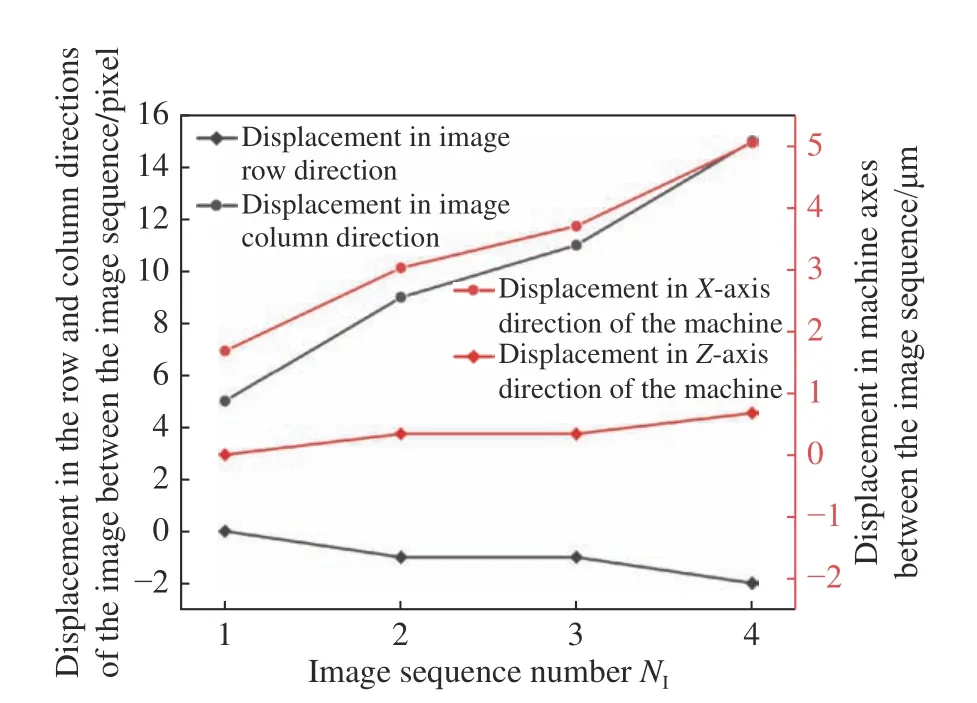
图14 图像序列间相对位移检测结果Fig.14 Relative displacement detection results between image sequences

得到图像序列间相对位移量检测结果后通过3.2 节中的位移补偿算法，即式（6），对图像序列间相对位移进行补偿，并使用式（7）更新变形前后图像区域。同时，将更新的变形前后图像区域大小缩小为1 301×1 301，行列方向对应原图像区域的坐标范围都是500～1 800。为测试位移补偿后，刀具与工件之间相对运动的转换效果，以及对由外界环境中的振动所引起的图像序列间的位移误差补偿效果，在更新后的图像序列间起始图像中，对应地在工件和刀具区域选取两个检验区域IVW 和IVT，位置和大小如图15 所示。对这两个区域再次进行相对位移量检测，得到的测量结果如图16 和图17 所示。

图15 位移补偿效果验证截取模板图像Fig.15 Intercepted template image in the verification of the displacement detection compensation effect

图16 更新图像序列中二次模板匹配结果Fig.16 The secondary template matching results in the updated image sequence

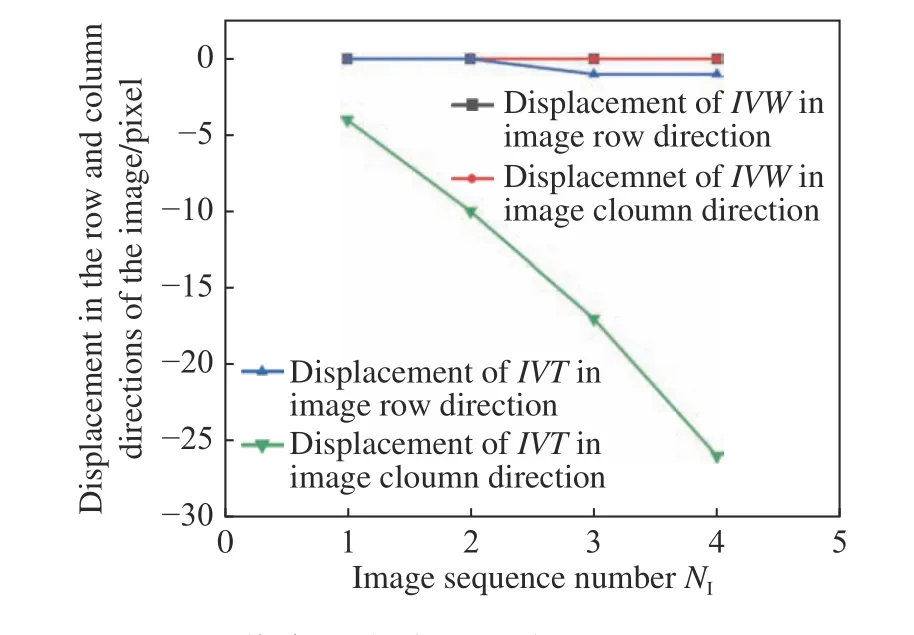
图17 更新图像序列中检测区域IVW 和IVT 上的相对位移量Fig.17 The relative displacements between the detection regions IVW and IVT in the updated image sequence

图16 中为所截取的模板图像IVW 和IVT 在更新后的图像序列中搜索匹配的结果，包括模板图像所处位置POS以及最大相似系数R。由图17 中曲线变化可知，使用上述提出的图像序列间相对位移的检测和补偿方法对切削过程图像序列处理后，已经将主切削运动形式由刀具静止，工件沿机床X轴正向（图像列方向正向）运动转换为工件静止，刀具沿X轴负向（图像列方向负向）运动；同时，由工件检测区域IVW 行列方向位移全为零可以看出，由外界环境中的振动引起的图像序列间工件的位移波动也得到了很好的补偿，由于工件与刀具之间切削力的相互作用，致使刀具检测区域在机床Z 轴正向（图像行方向负向）存在微小位移。

对更新前后图像序列（分别对应图9、图15和图16）的切削过程采用DIC 进行位移场分析，为便于表述图像序列中变形区域内位移场的分布，选取图像左下角顶点作为整个图像域的起始点，图像行方向、列方向分别以向上和向右为正,与机床的X，Z轴正方向相同。选取的两张变形区位移场DIC 分析图像在更新前后的图像序列中对应的序列编号NI同为0 和1,且变形参考图像对应的序列编号NI同为0。变形分析区在变形参考图像中所处位置（左上角顶点处像元）为POS:(793,572)，大小为201×489。使用2.2 节中的DIC 求解算法对选取的两组图像进行变形区位移场分析得到的位移场分布结果如图18、图19 所示。

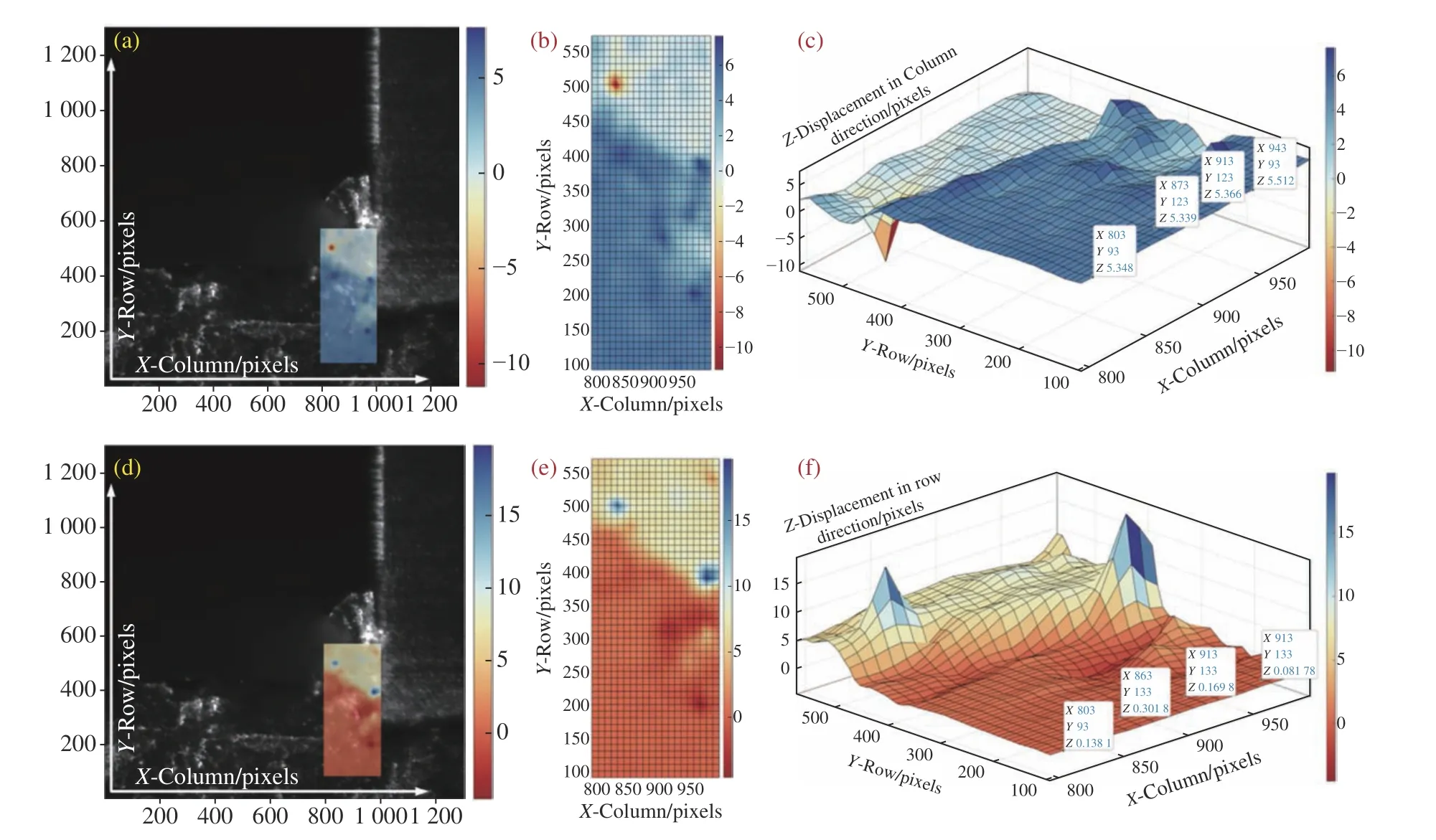
图18 位移补偿前DIC 分析变形区位移场分布结果。（a）列方向位移场变形参考图像中显示；（b）列方向位移场二维云图；（c）列方向位移场三维曲面图；（d）行方向位移场变形参考图像中显示；（e）行方向位移场二维云图；（f）行方向位移场三维曲面图Fig.18 Displacement field distribution results of the deformation area without displacement compensation.(a) The column direction displacement field in the deformed reference image;(b) two-dimensional cloud map of the displacement field in the column direction;(c) surface plot of the column direction displacement field;(d) the row direction displacement field in the deformed reference image;(e) two-dimensional cloud map of the displacement field in the row direction;(f) surface plot of the row direction displacement field

由于在所选变形分析区的行方向下边界处材料变形量小，其位移值主要受工件切削进给运动的影响，因此，在此处等间距抽取4 个点，通过对比这4 个点的位移值，分析图像序列间进行相对位移补偿对变形区位移场DIC 分析结果的影响。如图18(c)所示，未进行位移补偿的图像序列变形区下边界4 点列方向上的位移值为5.339～5.512；如图18(f)所示，行方向上位移值为0.081 78～0.301 8，对应的单位都为1 个像元尺寸。由于变形区行方向下边界处远离刀具前刀面和刀尖，因此在切削过程中几乎不会产生变形，其相对于工件未变形区的位移值应该接近0。同时，通过对比图14 中图像序列间的相应位移量，可以看出由于未进行位移补偿，变形区列方向位移场取值主要受工件进给运动和外界环境振动的影响，变形区行方向取值主要受到外界环境中振动的影响。经过位移补偿的变形区下边界处4 点的列方向、行方向上的位移值分别为0.329 7～0.511 8 和0.081 83～0.303 1，如图19(c) 和图19(f)所示。因此，可以得出通过上述图像序列间的位移检测及补偿算法，能够对工件的进给运动和外界环境中振动的影响进行有效的补偿校正，使变形区的位移场分布结果更为直观，便于分析微细正交切削过程中在刀具的切削作用下工件材料的变形过程。

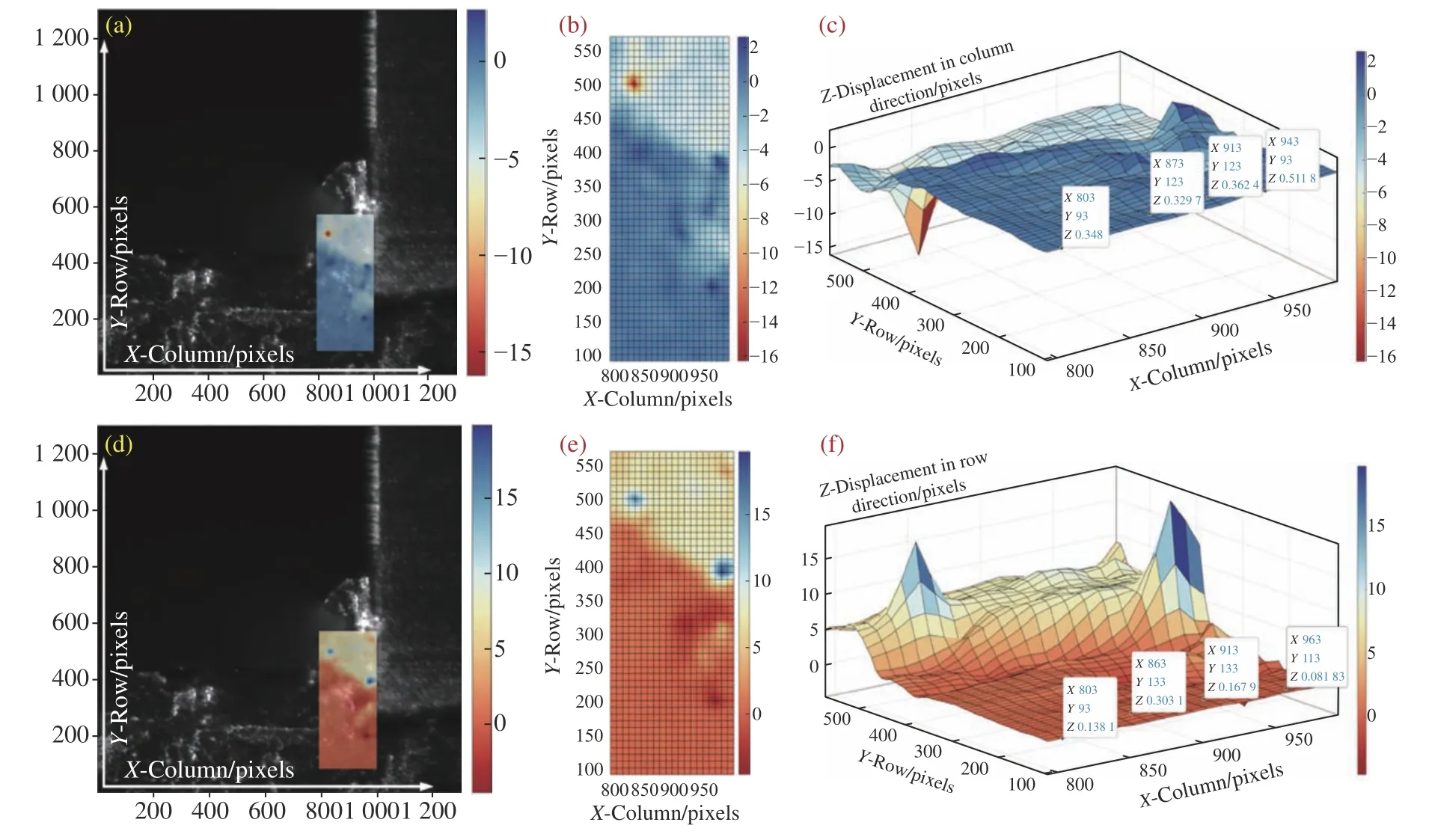
图19 位移补偿后变形区位移场分布结果。（a）列方向位移场变形参考图像中显示；（b）列方向位移场二维云图；（c）列方向位移场三维曲面图；（d）行方向位移场变形参考图像中显示；（e）行方向位移场二维云图；（f）行方向位移场三维曲面图Fig.19 Displacement field distribution results of the deformation area with displacement compensation.(a) The column direction displacement field in the deformed reference image;(b) two-dimensional cloud map of the displacement field in the column direction;(c) surface plot of column direction displacement field;(d) the row direction displacement field in the deformed reference image;(e) two-dimensional cloud map of displacement field in the row direction;(f) surface plot of row direction displacement field

5 结论

本文针对微细正交切削变形区位移场原位观测分析中由工件进给运动和外界环境中振动引起的图像序列间的位移偏差进行补偿，基于图像尺寸压缩和运动约束，提出一种新的图像序列间相对位移快速搜索匹配计算以及补偿算法，通过与常规归一化模板匹配算法进行对比验证可知：所提新算法的相对执行效率Rer最大提升至7 157.3～8 361.6；同时，其位移补偿精度达到1 个像元尺寸以下，为0.336 7μm。在保证大观测视野和不改变变形区照明光场强度分布的情况下，将切削工况由工件做进给运动转化为刀具做进给运动。通过对比图像序列间相对位移补偿前后的位移场分布情况，可以看出经过位移补偿后变形区未变形部分受位移偏差影响最大的方向位移由5.339～5.512 个像元尺寸，补偿为0.329 7～0.511 8 个像元尺寸；去除位移偏差影响，在刀具切削作用下变形区工件材料间的相对位移变得更为清晰直观。