面向Kullback-Leibler 散度不确定集的正则化线性判别分析

梁志贞 张 磊

如今利用现代设备采集高维数据变得方便和容 易,但是获得的高维数据可能包含不相关和冗余的信息.这不仅增加了学习模型的计算量和存储量,而且可能导致学习模型的性能下降.为了解决这些问题,线性降维[1-4]通常用于从数据中提取重要和有用的信息.线性降维的目的是通过优化一些准则函数对原始特征空间进行适当的线性变换.主成分分析(Principal component analysis,PCA)和线性判别分析(Linear discriminant analysis,LDA)是两种流行的线性降维方法.由于PCA 和LDA 的简单性和有效性,它们已经被广泛应用于许多领域,如人脸识别[5]、手写体字符识别[6]和缺陷诊断[7]等.

当样本的类别信息可用时,通常情况下LDA在提取数据的鉴别特征方面比PCA 更有效.线性判别分析的目标是在变换空间中通过最大化类间距离和最小化类内距离来寻找投影矩阵.从概率的观点来看,假设每类样本服从高斯分布且具有不同的类中心以及相同的协方差,则从Bayes 最优准则可推导出LDA.

为了改善线性判别分析的特征提取性能,各种LDA 的改进算法[8-10]已经被提出.使用最优向量替换各类中心[8]能提高LDA 的类信息鉴别能力.分数阶的LDA[11]通过在一系列分数阶中引入加权函数来改善LDA,但这增加了获得投影向量的代价.与Bayes 错误率相关的近似成对精度准则[12]在原空间计算各类的权重,从而改善LDA 的性能.几何平均[13],调和平均[14]以及加权调和平均[15]被用来定义判别分析的准则函数.最不利情况下的线性判别分析[16]考虑了最近的两个类中心和具有最大方差的类来寻找投影方向.基于最大-最小距离的目标函数[17]探索了最近的数据对的性质来取得投影方向.Wasserstein 判别分析[18]利用正则化Wasserstein 距离获取类之间的全局和局部信息并优化目标函数取得最佳投影方向.

线性判别分析存在小样本的奇异性[19]以及非线性数据特征提取[20-21]等问题.为了克服LDA 的小样本奇异性问题,典型的方法包括PCA+LDA,正则化LDA,伪逆LDA 以及张量判别分析[22]等.为了有效地处理非线性数据,各种线性判别分析已被拓宽到基于核函数的判别分析[7,20-21].当训练集随着新数据的加入而变化时或处理的数据量大时,各种增量学习[23-24]或在线学习方式被用来获得鉴别分析的投影方向.文献[24] 提出了两种形式的增量LDA :序列增量LDA 和块增量LDA,它们能有效地获取大数据流的特征空间.

数据在采集或传输过程中可能受到污染,这使得处理的数据包含噪声或离群点.但经典线性判别分析对噪声数据具有敏感性,即获得的投影方向偏离真正的投影方向.为了降低LDA 对噪声数据的敏感性,许多工作致力于用鲁棒的目标函数替换LDA的原有目标函数[25-26].已有的诸多研究发现,基于L1范数的目标函数比基于L2范数的目标函数在抑制异常点或噪声方面更有效[27-29].因此基于L1范数的判别分析方法近年来备受关注.L1范数的LDA[28]的类内距离和类间距离的定义依赖于L1范数,这在某种程度上能抑制噪声.L1范数的核LDA 不仅能抑制噪声,而且能捕捉数据的非线性鉴别特征[28].L1范数的两维LDA[30]拓宽了L1范数的LDA,这种方法可直接处理图像数据,而不需要把图像转化为向量形式.通常L1范数的判别分析通过贪婪算法获取多个投影方向,而非贪婪迭代算法[31]被用来直接获取L1范数的LDA 的多个投影向量.广义弹性网[32]通过Lp范数定义的目标函数来改善判别分析抑制噪声的能力,而通过优化Bhattacharyya 的L1范数误差界[33]可设计出新的鉴别分析模型.最近提出的基于L21范数的LDA 方法[34]通过同时优化类中心和投影方向从而在噪声数据方面表现出良好的性能.

在大多数判别分析中,通常假定类内各个样本以相等的概率(均匀分布)取得的,但是位于类中心附近的样本一般远远多于位于类边界附近的样本.为了增加类内样本采样的多样性,可令类内样本的采样概率在均匀分布的概率附近变化,这种变化有利于区分类中心附近的样本或类边界附近的样本.不确定优化中的不确定集能描述概率分布的变化范围.因此本文借助KL 散度定义的不确定集对类内样本信息进行概率建模.此外,为了更好描述各类中心的信息,本文也利用KL 散度定义的不确定集对其进行概率建模.基于此,本文提出了基于KL散度不确定集的线性判别分析方法,从而进一步改善已有线性判别分析方法.与以往的方法不同,本文不仅考虑了一般范数的目标函数,而且利用不确定集对训练样本信息进行了刻画.本文采用的不确定集为围绕均匀分布的KL 散度球且约束中的不确定集被转化为目标函数的正则化项.本文的主要贡献表现为:

1) 提出了正则化对抗LDA 和正则化乐观LDA.正则化对抗LDA 优先考虑了难以区分的样本,而正则化乐观LDA 优化考虑了易于区分的样本.

2) 采用了广义Dinkelbach 算法求解正则化对抗LDA 或正则化乐观LDA.对正则化对抗LDA运用投影梯度法求解优化子问题,而对正则化乐观LDA 运用交替优化求解优化子问题.

3) 在数据集上表明了当数据没有被污染时,两种判别分析模型取得可竞争的性能,但在污染数据的情况下,正则化乐观LDA 取得更好的性能.这也从另一方面说明了本文提供两种模型的目的,即如果在某些验证数据集上正则化乐观LDA 的最好性能明显优于正则化对抗LDA 的最好性能,那说明训练集包含离群点.因此通过检查正则化对抗LDA和正则化乐观LDA 的性能可判断训练集是否包含离群点.

1 相关工作

1.1 最不利情况的线性判别分析

在文献[16]中,类间离差矩阵(1)被改写成下面形式:

其中W是一个d×m投影矩阵以及Im表示单位矩阵.在投影空间中,模型(4)通过优化距离最近的两个类中心和具有最大类内距离的类取得最优投影矩阵.这种方法实际上寻找不利区分样本的最优投影方向.这种设计思想来源于分类器的设计.在分类器设计中,设计的分类器对难以分类的样本(边界样本)进行优先考虑,即赋予较大的采样概率,从而使设计的分类器具有更好的泛化性能.模型(4)通过优先考虑难以区分的样本取得最优投影矩阵.Zhang和Yeung[16]提出了两种算法求解模型(4).一种方法是将(4)转化为度量学习问题,另一种方法是设计了一种基于约束的凹凸优化算法.

1.2 基于L1 范数的线性判别分析

在文献[28]中,下面优化模型被用来取得投影矩阵W:

其中 ‖·‖1表示向量的L1范数,li表示第i类样本的集合.优化问题(5)的目标函数关于变量W是非平滑和非凸的.文献[28]首先利用梯度上升法取得一个投影向量,然后设计了一个贪婪方法来取得多个投影向量.

1.3 基于L21 范数的线性判别分析

为了改善线性判别分析模型在投影空间的鉴别能力,文献[34]提出了下面的优化模型:

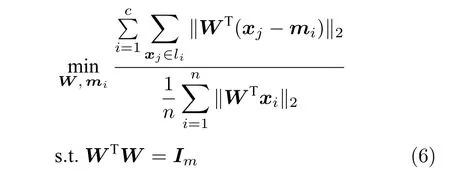
与以前的一些模型不同,式(6)的类平均mi(i=1,···,c)是优化变量.模型(6)的目标函数实际上对不同样本采用了L1范数,而对每个样本的约简特征采用了L2范数,这通常被称为L21范数的线性判别分析.如果数据包含离群点,基于算术平均取得的类中心可能偏离样本的真正类中心,而优化的类中心接近真正的类中心.模型(6)比模型(5)包含更多的优化变量.文献[34]设计了一个有效的框架求解模型(6).

2 基于不确定集的正则化线性判别分析

2.1 正则化对抗LDA

为了度量两个具有公共支集的离散概率分布之间的差异,文献[35]定义了KL 散度.假设给定两个离散概率分布p=(p1,···,pn)和q=(q1,···,qn),那么这两个概率分布之间的KL 散度被定义为:

如果两个离散概率分布相同,则KL 散度的值为零.由于KL 散度不满足三角不等式,它实际上不是一个真正的距离度量.注意到KL 散度是非对称的,即KL(p|q)KL(q|p).KL 散度是非负的,即KL(p|q)≥0.在鲁棒优化中,基于KL 散度的不确定集被定义为[36-37]:

式(8)的不确定集表明,离散概率分布p在给定的离散概率分布q附近变化,其变化范围由一个非负参数ε控制.参数ε越大,不确定集的变化范围越大.单个p是不确定集内的一个具体的概率分布.

为了探索样本的类间信息,模型(4) 试图在低维投影空间中最大化最近的两个类中心,而且它利用L2范数定义了类间距离.在Ls范数的距离测度下,与式(4) 相似的类间信息的优化问题在WTW=Im约束条件下被写成下面形式:

模型(9)不仅引入了优化变量pij,而且在投影后的类间距离使用了Ls范数.如果s=1,那么使用了L1范数定义了类间距离.如果s=2,那么使用了L2范数定义了类间距离.模型(9)说明了优化变量pij在概率单纯形内变化,即在这个单纯形中寻找距离最近的类中心对,并试图取得最优投影矩阵.因此在提取鉴别特征时,距离最近的两个类中心所起的作用最大.显然,它忽略了其他类中心的信息,使得这种模型利用类中心的信息不完整.为了解决这个问题,本文首先将离散概率分布pij看作类中心mi和mj之间的采样概率,然后将离散概率分布pij限制在一定的范围内,使得模型变得更加灵活.这里使用式(8)定义的不确定集,这个不确定集是由离散概率分布定义的.因此根据KL 散度定义的不确定集和各类中心信息,以下优化问题被提出:

模型(12)采用了Lr范数定义类内距离,参数r是正的实数.模型(4)中分式的分母考虑了低维空间中具有最大类内距离的类,而模型(12)考虑了每一类中远离其类中心的那些样本,那些样本可能位于类之间的交界处.换言之,它搜索一些样本,使它们在类内信息中起主导作用.这样uik可看成第i类的第k个样本的采样概率.通过将uik限制在一个不确定集内,使样本的采样概率发生变化.根据(12)和不确定集可定义如下的优化问题:

式(19)和(20)实际上求解模型(14)的内层优化问题.利用式(19)和(20),优化模型(14)被改写成下面形式:

模型(21)仅包含优化变量W.它是一个非常复杂的非线性优化问题.从模型(21)的约束来看,它属于Stiefel 流形上的优化问题[41].

2.2 求解优化模型(21)

算法1 把比率优化问题(21)归结为两个函数差的优化问题.文献[27]已采用这种思想求解L1范数的LDA,从而避免矩阵逆的计算,这也克服小样本的奇异性问题.文献[27]的方法实际上是广义Dinkelbach 算法的一种形式.这样本文的算法也不会出现矩阵逆计算问题.如果KL 散度的值不为0,F1(W,pij)作为式(14)的分母也不为零.这些因素促使了提出的算法克服了小样本的奇异性问题.

2.3 正则化乐观判别分析

正则化对抗判别分析探索了不确定集中的对抗概率分布,这实际上优化考虑了训练集中位于类边界附近的样本(远离类中心的样本).然而当数据集包含离群点时,这些离群点可能远离各类中心.在这种情况下,优先考虑类中心附近的样本是有益的,即对接近类中心附近的样本分配大的采样概率.不同于第2.1 节中的模型,本小节试图在不确定集中寻找另外一种概率分布,这对应于优先考虑类中心附近的样本点.因此借助不确定集以及类内和类间信息可定义以下优化问题:

模型(23)优先考虑了距离大的类中心对,这实际上优先考虑区分性比较好的类.因为KL(p|q)取非负值,这不能从H1(W,pij)的定义得出其非负性.对于模型(24),它优先考虑区分性比较好的样本,即对类中心附近的样本赋予大的采样概率和类边界附近的样本赋予小的采样概率.当处理的数据包含异常点或噪声时,它优先考虑了那些可能不是异常点的样本,即对异常点赋予小的采样概率.因为KL 散度是非负的,从式(24)知,H2(W,uik)不小于零.根据(23)和(24)可建立以下单目标函数:

从(23),(24)和(25)知,外层优化(优化W)和内层优化(优化uik,pij)的目标有一致的性质.根据不确定规划中的乐观模型的概念,本文将模型(25)称为正则化乐观LDA(Regularized optimistic LDA,ROLDA).内层优化取得的概率分布被称为不确定集的乐观概率分布.模型(25)利用不确定集优先考虑类中心附近的样本点.对训练集而言,模型(25)优先考虑了区分性好的类和样本.如果数据集包含异常点或噪声,那么这些异常点或噪声可能远离类中心且具有较低的采样概率.因此模型(25)在某种程度上能抑制异常点或噪声.模型(25)是非凸优化问题,同样地也采用了广义Dinkelbach 算法求解模型(25).求解式(25)涉及下面优化子问题:

模型(29)属于约束的最小化问题.因为约束集是闭有界集且目标函数是连续的,模型(29)存在解.注意到优化变量uik,pij以及W的约束是独立的,这样交替优化算法能有效地求解模型(29).模型(22)仅涉及优化变量W且目标函数是复杂的非线性优化问题,但模型(29)涉及三组优化变量,每一组优化变量对应一个优化子问题.算法3 概括了求解模型(29)的过程.

算法3.求解式(29)的交替优化算法

如果s=r=2,算法1 中的步骤a) 可通过特征值分解取得投影矩阵W.在其他情况下,可通过在Stiefel 流形上的梯度下降法取得投影矩阵W.不同于正则化对抗LDA 的求解,如果采用Stiefel流形上的梯度下降法取得W[41],此时函数的梯度并不包含指数函数,这实际上把指数函数放在了pij和uik的更新上.在s=r=2 情况下,取得W的计算复杂度为 O (d3).当样本的维数较大时,执行特征值分解可能比较耗时,那么可采用流形上的梯度下降法取得W.采用Stiefel 流形上的梯度下降法取得W的复杂度为 O (Tg(c2dm+ndm)),其中Tg为梯度下降法的迭代次数.更新pij和uik的计算复杂度分别 为 O (c2dm) 和 O (ndm).这 样如果s=r=2 且 采用特征值分解取得投影矩阵W,那么算法的计算复杂度为 O (T3(c2dm+ndm+d3)),其中T3为算法3的迭代次数.如果采用Stiefel 流形上的梯度下降法取得投影矩阵W,那么算法3 的计算复杂度为O(T3(c2dm+ndm+Tg(c2dm+ndm))).

2.4 与其他线性判别分析的关系

从式(17)和(18)可得到如下推论.

推论1 说明了当参数η和λi趋向正无穷大时,pij和事先定义的qij一致,以及uik和事先定义的vik一致.在这种情况下,根据qij和vik定义可得出pij=2/(c(c-1)) 和uik=1/ni.此时正则化对抗LDA 退化为不同范数的LDA.即当s=r=2 时,模型(14)成为L2范数的LDA;当s=r=1 时,模型(14) 成为L1范数的LDA.当参数η和λi趋向0 时,模型(14)变成了最强对抗概率分布下的线性判别分析.这样参数η和λi的变化为模型(14)和各种范数的LDA 建立了联系.因此RALDA 推广了以前的模型.

从式(27)和(28)可知:当参数η和λi趋向正无穷大时,pij=2/(c(c-1)) 和uik=1/ni.此时正则化乐观L D A 退化为不同范数的L D A.即s=r=2时,模型(25) 成为L2范数的LDA;当s=r=1时,模型(25)成为L1范数的LDA.当参数η和λi趋向0 时,模型(25)变成了最乐观概率分布下的线性判别分析.从式(17) 和(18),以及式(27)和(28)可知,RALDA 和ROLDA 中的pij和uik是不同的.从(17)可知类边界附近的样本具有大的采样概率;从(28)可知类中心附近的样本具有大的采样概率.这样模型(14)优先考虑那些不利区分的样本,而模型(25)优先考虑了那些有利区分的样本.尽管这两种模型的机制是不同的,但是当参数趋向无穷时,它们是等价的.

3 实验结果

本节通过在数据集上的一系列实验来评估所提出模型的有效性.当涉及到分类问题时,本文采用了最近邻分类器且度量准则采用了欧氏范数.为了进行比较,本文编程实现了几种鲁棒的特征提取方法,包括L1-LDA[6]、最不利LDA (Worst-case LDA,WLDA[16])、LDA-L1[28]和L21-LDA[34].L1-LDA 和LDA-L1 的参数设置与文献[34]中的相同.注意到提出的模型涉及多个参数.为了简单起见,令参数λ=λ1=···=λc,即所有的类都被赋予了相同的参数λ,这样模型的参数被约简为两个参数λ和η,两个参数取自集合{10-3,10-2,10-1,1,10,102,103}.对于参数r和s,本文只考虑参数取特殊值的情况,即把s=r=1 和s=r=2 的RALDA 分别简记为L1RALDA 和L2RALDA,以及 把s=r=1 和s=r=2的ROLDA 分别简记为L1ROLDA 和L2ROLDA.迭代方法的初始解采用了LDA 的正交化投影矩阵.实验环境是一台内存为8 GB 的奔腾1.6 GHz 计算机和Matlab (7.0.0)编程语言.

3.1 人脸和物体数据集的实验

本小节在四个人脸数据库(Yale、ORL、UMIST 和AR)上和一个物体数据库(COIL)上测试了提出的模型.ORL 人脸数据库包含40 个人,每个人都有10 幅不同的图像,所有的图像都是在一个均匀背景下拍摄的.UMIST 人脸数据库包含20 个人的564 幅人脸图像,每个人都有不同的种族、性别和外貌,例如不同的表情、照明、戴眼镜/不戴眼镜、留胡须/不留胡须、不同的发型.耶鲁大学的人脸数据库包含15 个人的165 幅灰度图像,其人脸图像涉及光照条件和面部表情的变化.AR 人脸数据库包含4 000 多幅彩色人脸图像,每个人有不同的面部表情、光照条件和遮挡.AR 人脸图像在两个不同的时间段拍摄且时间间隔是两周,每阶段获取每个人的13 幅图像.COIL 数据库包含1 440 幅灰度图像和20 个物体的黑色背景,每个物体有72 幅不同的图像.为了提高计算效率,将所有图像归一化为 32×32 大小的灰度图像.

考虑到提出的算法是一种迭代算法,第一组实验测试了算法的收敛性.实验数据来自Yale 数据集.我们随机选取每个人的四幅图像组成训练集,其它图像用于测试.假设约简维数为14.训练集中有一半的样本被矩形噪声污染.矩形噪声包含等概率的白点和黑点,它们在图像中的位置是随机的且块的大小是 32×32 像素.在实施算法2 时,令β=0.5.图1 列出了L2RALDA,L1RALDA,L2ROLDA和L1ROLDA 四种方法的收敛性.为了简单性,在这组实验中令λ=η.

从图1 可知,四种算法的目标函数值随着迭代次数的增加而递减.当迭代次数超过某一数值时,目标函数值几乎保持稳定.文献[27]指出:当出现小样本的奇异性问题时,采用梯度上升法求解L1范数的判别分析(目标函数为最大化问题)可能使得目标函数值发生振荡现象.在这组实验中,图像的维数远远大于训练样本的个数,这存在奇异性问题,但图1 显示了提出的算法的目标函数值并没有出现振荡的情况,这意味着提出的算法在某种程度上避免了小样本的奇异性问题.从图1 可观察到基于L1范数的模型比基于L2范数的模型一般需要更多的迭代次数,这是因为基于L1范数的模型有不可微的目标函数.注意到不同的参数也影响算法的收敛速度.因此在后面的实验中,本文设定算法的停止条件为最大迭代次数为50 或目标函数值的相对改变不超过 10-4.

图1 L2RALDA,L1RALDA,L2ROLDA 和L1ROLDA 的收敛性分析Fig.1 Convergence analysis of L2RALDA,L1RALDA,L2ROLDA and L1ROLDA

在约简的参数下提出的模型有两个重要参数λ和η.这组实验探索了参数λ和η对识别性能的影响.对于图像识别问题,为了降低计算代价,采用主成分分析降维但保持图像的百分之九十九的能量.对于耶鲁数据集,随机选取每个人的四幅图像组成训练集,其他样本用于测试.假设约简维数为14,固定r=s=1 或r=s=2,参数λ和η从集合{10-3,10-2,10-1,1,10,102,103}中取值.因此每个参数取七个值.实验结果来自十次的平均实验.图2显示了每种算法随参数变化的错误率.在图2 的每个子图中,其中x轴表示对数尺度的参数λ,y轴表示对数尺度的参数η,以及z轴表示算法的错误率.

从图2 可看出,模型的错误率随着参数的变化而变化.当参数λ和η取较小值时,L1ROLDA 的错误率较低.对于L2ROLDA,如果参数η取较大值且参数λ取较小值,则分类性能较好.对于L1RALDA,如果参数η取较小值且参数λ取较大值,则在很大范围内获得较低的错误率.对于L2RALDA,其参数也影响算法的性能.这组实验表明了L1ROLDA和L1RALDA 的作用机理是不同的.因此在实际应用中需要选择合适的参数才能获得最佳的分类性能,这可通过交叉验证等方法来获得最佳参数.

图2 L2RALDA,L1RALDA,L2ROLDA 和L1ROLDA 的错误率与参数的关系Fig.2 Error rates of L2RALDA,L1RALDA,L2ROLDA and L1ROLDA versus the parameters

为了比较各种模型的特征提取性能,在Yale、ORL、UMIST 和COIL 数据集上随机选取每个人的4 幅图像构成训练集,其余图像用作测试目的.为了评价算法的鲁棒性,在Yale、ORL、UMIST 和COIL 数据集上人工模拟了遮挡图像,那就是训练集中有一半的样本被矩形噪声污染.矩形噪声包含等概率的白点和黑点,它们在图像中的位置是随机的,块的大小是 20×20 像素.由于AR 数据集包含实际遮挡的情况,本文考虑了120 个人的两种遮挡情况:其一是太阳镜遮挡,其二是围巾遮挡.在AR数据集上,对于太阳镜遮挡,从第一时间段的7 幅无遮挡图像中随机选择3 幅图像,然后将这些图像与随机选择的3 幅太阳镜遮挡的图像构成训练集.第二时间段得到的7 幅无遮挡的图像被用做测试集.因此每个人的训练样本数为6.对于围巾遮挡,从第一时间段的7 幅无遮挡图像中随机选择3 幅图像,然后将这些图像与随机选择的3 幅围巾遮挡图像构成训练集,第二时间段得到的7 幅无遮挡的图像被用做测试集.

图3 显示了在Yale 数据库上几种算法的错误率随约简特征变化的情况.表1 列出了各种方法的最好性能.另外表1 中给出了各个人脸数据集上和COIL 数据集上的最好性能.每种方法的参数在额外的五次运行上得到.表1 的实验结果来自20 次随机运行的平均,其中C-表示污染的数据集.

图3 数据集上不同方法随维数变化的错误率Fig.3 Error rates of various methods with varying dimensions on the Yale database

从图3 可知,随着约简维数的增加各种方法的错误率下降,但过多的特征反而使得错误率上升.这表明特征的维数是一个重要的参数.从表1 可看出,对于原图像集,L1RALDA 在ORL 和UMIST数据集上可获得很好的分类效果,这表明在适当的条件下,优先考虑边界点的判别分析算法是合理的.当部分图像被污染后,L1ROLDA 在大多数情况下优于其他方法.在实际遮挡的AR 数据上,围巾遮挡比太阳镜遮挡导致更大的错误率.

同其他方法比较,L1ROLDA 不仅采用了L1范数的损失函数,而且考虑了样本的采样概率,其采样概率在不确定集中自适应地变化,从而得到较好的效果.从表1 可知,当部分图像被污染后,各种方法错误率的标准偏差一般大于原始图像上各种方法错误率的标准偏差.这表明污染的数据使得各种方法的性能具有更大的不确定性.

表1 各种方法在原始数据集和污染数据集上的平均错误率(%)和标准偏差Table 1 Average error rates (%) of various methods and their standard deviations on the original and contaminated data sets

这组实验比较了各种算法在五个图像数据集上的时间消耗.提出算法的停止条件如前面所述.在ORL,UMIST,Yale 和COIL 数据集上假定约简维数为40.由于AR 数据集包含更多的类数,其约简维数设定为80.图4 显示了各种算法在五个数据集上的运行时间(单位:秒).

从图4 可看出,WLDA 的运行时间远远高于其它算法的运行时间,这是因为这种方法采用了二阶锥规划.L1-LDA 和LDA-L1 都采用了贪婪算法取得多个投影向量,它们的运行时间相差不大.在Yale 和ORL 数据集上,L21LDA 的运行时间是最少的,但在UMIST 和COIL 数据集上,L2ROLDA需要的时间最少.由于在AR 数据集上的约简维数为80 且类数较多,每种方法的训练时间明显大于在其他数据集上的训练时间.一般来说,L1RALDA和L1ROLDA 训练时间分别大于L2RALDA 和L2ROLDA 的训练时间,这是因为L1RALDA 和L1ROLDA 采用了L1范数导致其目标函数是不可微的,而L2RALDA 和L2ROLDA 的目标函数是可微函数.

图4 五个图像数据集上各种算法的运行时间Fig.4 Running time of various methods on five image data sets

3.2 UCI 数据集上的实验

这组实验使用的数据集来自UCI 机器学习库.这些数据集已被广泛用于评估一些学习算法的性能.本文在8 个数据集上测试了提出的模型.这8个数据集分别是Australia (690 样本/14 特征/2 类),Diabetes (768/8/2),German (1 000/24/2),Heart (270/13/2),Liver(345/6/2),Sonar(208/60/2),WPBC (198/33/2)和Waveform (5 000/21/3).不同于图像数据集,对于这些数据集,训练样本的维数远远小于训练样本的个数,即小样本的奇异性问题不会出现.每个数据集样本的属性被转化为[-1,1]区间.对于每个数据集,随机选取70%的样本构成训练集,剩下的样本作为测试集.除了原始数据集,我们也模拟了训练集中样本的某些特征被污染的情况.具体来说,训练集中一半样本的50% 特征被替换为由-1 和1 组成的随机噪声.

每种方法的参数在训练集上通过五叠交叉验证方法学习得到.实验性能取自十次随机实验的平均结果.为了比较两种算法在同一个数据集上的性能,在显著性水平0.05 的情况下计算L1ROLDA 和其他算法的配对t检验的p-值.如果p-值大于0.05时,这表明L1ROLDA 和其他算法没有显著的差别.当p-值小于0.05 时,这表明L1ROLDA 和其他算法存在显著差别.表2 和表3 列出在原始数据集和污染数据集上的实验结果,其实验结果包括平均正确率(Average correct rates,ACR)和标准偏差(standard deviations,SD)以及L1ROLDA 和其他方法的配对t检验的p-值.

从表2 可知,L21-LDA 在Diabetes 数据集上取得最好的性能,L1RALDA 在German 和WPBC 数据集上取得最好的性能,L1ROLDA 在Australian,Heart 和Waveform 数据集上取得最好的性能,L1-LDA 在Liver 数据集上取得最好的性能,这表明了没有一种方法在这些数据集上取得一致好的性能.从表3 可知,当特征被污染后,每种方法的性能都会存在某种程度的下降.一般来说基于L2范数方法不比基于L1范数方法好.从表2 和表3的p-值可知,L1ROLDA 和其它方法是否存在明显的差别.例如:从p-值可知在特征没有被污染的情况下,L1ROLDA 和L21LDA 在German 和Heart数据集上存在统计意义上的差别,但当特征被污染后,L1ROLDA 和L21LDA 在Australian,German,Heart,Liver 和Waveform 数据集上存在统计意义上的差别.

表2 各种方法在原始数据集上的平均正确率(ACR(%)),标准偏差(SD)和 p-值Table 2 Average correct rates (ACR(%)),standard deviations (SD),and p-values of various methods on the original data sets

表3 各种方法在污染数据集上的平均正确率(ACR(%)),标准偏差(SD)和 p-值Table 3 Average correct rates (ACR(%)),standard deviations (SD),and p-values of various methods on the contaminated data sets

当特征被污染后,L1ROLDA 方法在多数情况下优于其他方法,这是因为在不确定集下,优先考虑了那些有利区分的样本,这些样本可能不是污染的数据点,而对离群点赋予较低的采样概率.因此当数据被污染后,应当优先选择L1ROLDA 方法.实际上,当测试RALDA 和ROLDA 时,如果在验证数据集上ROLDA 的性能远远好于RALDA 的性能,那么说明训练集包含离群点.在这种情况下,我们可采用一些去离群点的方法去除训练集中的离群点,然后再执行特征提取算法.

尽管配对t检验能比较两种算法在同一个数据集上的性能差别,但是它不能取得多种算法在多个数据集上的性能排序问题.由于在多个数据集上测试了多种方法,本文采用Friedman 检验[40]评估多种算法的性能.在Friedman 检验中,如果零假设成立,即假设所有的算法在性能上是相等的,Friedman 统计量可用概率分布来计算.本文使用关键差别(Critical difference,CD)图[40]比较不同算法的性能.图5 表示了在原始数据和污染数据上的性能分析的CD 图.CD 图的平均秩提供了算法的性能的排序.平均秩越小,算法的性能越好.从图5(a)可知,L1ROLDA 给出了最小的平均秩,但是L21-LDA 的平均秩和L1ROLDA 的平均秩相差不大.WLDA 有最大的平均秩.从图5(b)可知,当数据被污染后,L1ROLDA 仍然取得了最小的平均秩,但L21-LDA 的平均秩明显大于L1ROLDA 的平均秩.总的来说,由于采用了L1范数和优先考虑了类中心附近的样本,当数据被污染后,正则化乐观线性判别分析取得最好的性能.

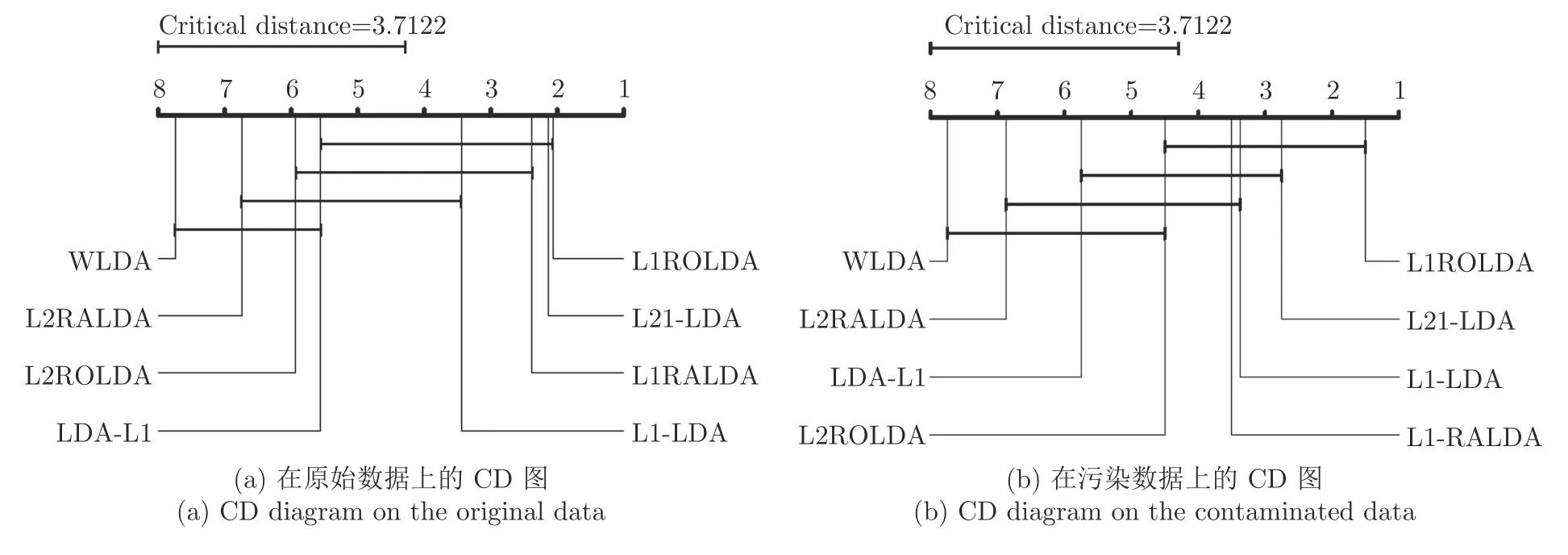
图5 不同方法性能的显著性分析Fig.5 Performance significance analysis of various methods

4 结论

本文提出了基于不确定集和混合范数的线性判别分析方法.不同于以前的方法,本文借助Kullback-Leibler 不确定集描述样本的变化信息,这样可探索不确定集中的概率分布.由于样本或类中心的采样概率在不确定集中灵活变化,从而使得模型适应数据的内在特性.模型是比率优化和非凸优化问题.广义Dinkelbach 算法被用来求解优化模型.本文利用投影梯度法或交替优化技术求解算法的优化子问题.这样算法的收敛性直接来自广义Dinkelbach算法的收敛性.在图像数据集和UCI 数据集上做了一系列实验.实验结果表明:在没有污染的数据集上,由于RALDA 考虑了类边界附近的样本,RALDA应当被优先考虑,但在污染数据集上,ROLDA 应当被优先考虑.由于本文简化了模型中一些参数,这些参数对模型的性能会产生一定的影响.今后我们将重点研究如何自动学习多个参数,并将本文的基本思想推广到其它基于核函数的非线性判别分析和张量判别分析.