引信殉爆阈值数值模拟
王 慧
(海军装备部装备审价中心,北京 100071)
当炸药发生爆炸时,爆炸所产生的爆轰波和爆炸碎片导致间隔一定距离的另一个炸药发生爆炸的现象,称为殉爆[1]。袁俊明等对裸装聚奥-9C(JO-9C)传爆药进行了引信殉爆数值模拟,分析了殉爆过程中JO-9C爆轰波的成长历程和传播规律[2]。KIM等利用流体动力学模型,分析了PBXN-9炸药一对多殉爆的影响因素[3-4]。陈朗等计算了不同距离下裸装固黑铝(GHL)炸药的殉爆距离,分析了炸药殉爆过程中被发炸药中爆轰波的成长历程[5-7]。文中通过冲击波作用传爆序列殉爆数值模拟,考虑导爆管的作用,获得了引信传爆管的殉爆距离和安全距离。
1 有限元模型
1.1 材料模型
利用Jones-Wilkins-Lee(JWL)描述起爆药的反应状态pe和未反应状态pg分别为:

式中:p为压强;V为相对比容;T为温度;A、B、R1、R2、ω和Cv为常数;下标e和g分别表示反应炸药和反应产物。
反应速率方程:
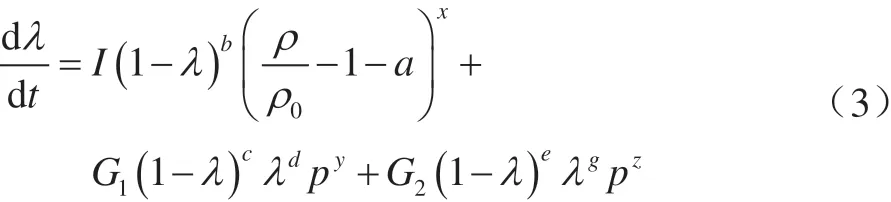
式中:λ为炸药反应度;t为时间;ρ为密度;p为 反 应 压 强;I、G1、G2、a、b、x、c、d、y、e、g和z为12个可调的拟合系数。
1.2 数值模型与方法
采用非线性有限元软件LS-DYNA 3D对引信传爆序列进行殉爆数值模拟。起爆点设置于起爆药上端中心点处,考虑爆炸冲击波对引信传爆序列的冲击作用,引信传爆序列结构如图1所示。传爆序列中,JH-14C的尺寸为38.0 mm 15.5 mm,并使用True Grid建立1/2三维有限元模型。
1.3 材料参数
各材料参数如表1和表2所示。导爆药、传爆药和起爆药分别为RDX-8701[8]、JH-14C和Comp B炸药。表1中,C、S1、γ0分别为格吕奈森方程截距、斜率和系数。表2中,Cp、G、SIGY分别为聚氨酯本构模型中的系数、剪切模量和屈服模量。

图1 引信传爆序列几何模型(单位:mm)
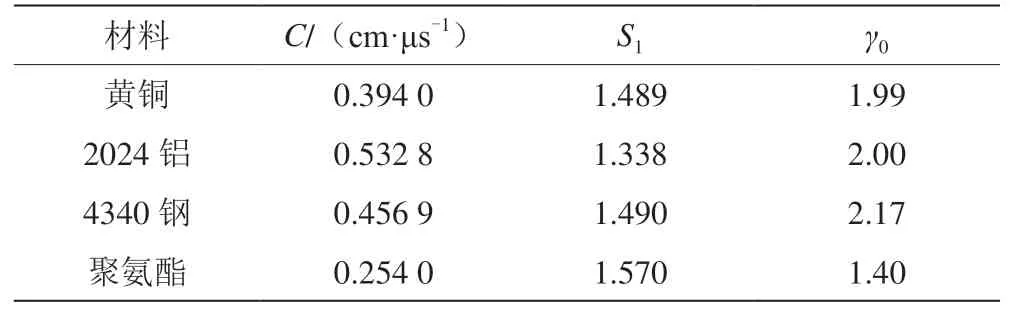
表1 紫铜、2024铝、4340钢与聚氨酯的格吕奈森状态方程参数

表2 聚氨酯本构模型参数
2 结果与讨论
表3为被发引信在不同距离下的爆炸情况。图2为距离9.5 mm处25 μs、40 μs时刻被发引信不同时刻的爆炸情况。图3为距离11.5 mm处25 μs、40 μs时刻被发引信不同时刻的爆炸情况。可见,t=25 μs时,主发冲击波作用于被发引信,在距离为9.5 mm、11.5 mm处,被发引信都发生了反应。但是,t=40 μs时,只有距离为9.5 mm处被发引信发生了殉爆,这是因为作用于被发引信的冲击波压强达到了传爆药的临界起爆压强[9-12]。

表3 不同距离下被发引信爆炸情况
通过设置高斯点来获取传爆药压强变化,高斯点的选取和压强曲线如图4(a)所示。图4(b)为距离9.5 mm处被发传爆药内部压强历程曲线。被发传爆药发生爆炸,初始峰值压强约为7.2 GPa。随着爆炸反应的进行,波阵面的压强越来越高。t=26.1 μs开始,压强值达到26.5 GPa,逐渐发展成稳定的爆轰波,直到在被发传爆药反应后期达到并稳定维持在JH-14C的爆压值27.67 GPa左右。图4(c)为距离11.0 mm处的压强历程曲线,可以看出t=26 μs时被发传爆药发生反应,爆轰波由左下向右上持续传播,但压强较低,初始峰值压强仅为3.26 GPa,爆轰波继续向右上传播,但炸药内部的压强值并无上升,反而呈现衰减趋势,被发引信未发生爆炸。

图2 9.5 mm不同时刻引信传爆序列爆炸结果
通过最小二乘法拟合,建立引信起爆的判据方法[13]:
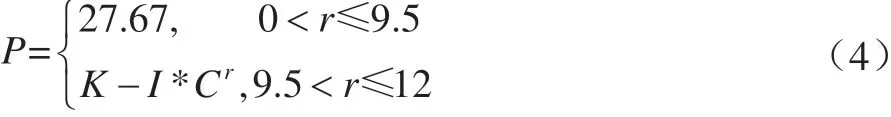
式中:K、I、C为判据的拟合参数,分别有K=3.425 61、I=-8.009 58 1016、C=0.023 25;P为压强峰值;r为引信传爆序列之间的距离。

图4 高斯点的选取和不同距离处传爆药压强历程曲线
3 结语
本文对引信传爆序列在冲击波单独作用下的情况进行了殉爆数值模拟,得到了临界殉爆距离和殉爆安全距离,并结合模拟结果,通过最小二乘法给出了引信起爆判据方法,可为引信传爆序列的装药设计、包装设计、生产贮存以及防护提供一定的参考。

