内置弧形槽扭旋元件圆管中湍流传热特性研究

张春梅，刘彬，李宇轩，李权，杨鹏达，李帅

（沈阳化工大学 机械与动力工程学院，辽宁 沈阳 110142）

能源的转换和利用是当今社会发展的关键性问题，而热能在各行各业中都占有举足轻重的地位，合理高效的换热设备可以极大促进热能的有效利用[1]，换热管作为换热设备中的重要元件，其传热性能直接决定换热设备的高效与否，因此研究出具有高传热效率的换热管成为该领域内的热点。

目前强化传热技术主要分为无源技术和有源技术两种[2-3],本文主要采用管插件无源技术进行强化换热，其作用机理为管插件的合理结构使流体在流经元件时产生径向流动的同时引起二次流[4-7]，此种流动现象会使管道中心流体与壁面附近的高温流体进行充分混合，同时壁面处的边界层也遭到破坏，有利于热量的传递与交换。

由于管插件技术经济高效、易于维修等优点，许多学者对其进行了大量研究。Kumar 等[8]在雷诺数为1～25 000 的范围内研究了SK 型静态混合器的长宽比及单元数量对流体流动和混合的影响，同时对比了元件在不同流态下的混合程度，并通过实验得出了每混合器单位的压降与所用SK 元件的数量无关的结论。P.Murugesan 等[9]研究了不同扭曲比、深度和宽度比的“V”型双绞扭带对圆管内的传热和摩擦系数的影响，研究发现管内平均努塞尔数和平均摩擦系数随扭曲比、宽度比和深度比的减小而增加。詹三江等[10]在光滑扭带的基础之上研究并分析了开三角形边槽的扭带新结构，实验证明了这种新型结构可以增加换热效果和沿程阻力，并与光滑纽带进行对比，定量分析了阻力系数λ与Nu增加的幅度，并得到了相应的努塞尔数Nu及阻力系数λ的实验关联式。孙达等[11]对高黏度下中国结式静态混合器的流动特性进行了模拟，发现Re较低时，中国结式静态混合器可以改变流场结构，促进径向混合并减薄边界层，强化高粘流体的混合及传热性能。

本文设计出一种由带有弧形凹槽的波纹板扭旋而成的新型管内扰流元件——弧形槽扭旋元件，探讨了弧形槽扭旋元件强化传热的机理，研究了弧形槽数量的变化对管内传热性能的影响。研究结果可为弧形槽扭旋元件在工程中的应用提供理论基础和技术支持。

1 物理模型及数值模拟

1.1 物理模型

本文研究对象为内含4 个扭旋元件的换热管道，相邻元件交错垂直布置，元件直径D，厚度δ，长度H，扭转角为180°，弧形槽的直径d，弧度R=π，弧形槽数量n分别为1、2、3，其中n=2 元件结构如图1所示。

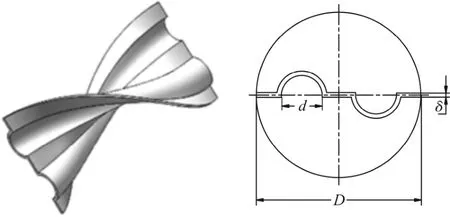
图1 n=2 弧形槽扭旋元件结构示意图

图2显示了扭旋元件在管道中的布置情况及三维坐标分布，管长为L，管径D，管道入口段和出口段均保留La。元件及管道的结构参数如表1所示。

表1 结构参数

图2 弧形槽扭旋元件管内分布示意图

1.2 数值模拟方法

1.2.1 模型假设

本文在数值模拟过程中做了如下假设：

1）流体为不可压缩的牛顿流体。

2）流体流动时为稳态。

3）忽略流体物性随温度的变化。

4）忽略自然对流及热辐射。

1.2.2 模拟方法

本文选用的工作流体为水，在雷诺数为4 000～10 000 的范围内进行研究，选用reliablek-e湍流模型，该模型可以更好地模拟旋转流动和二次流，使用标准壁面函数对近壁区域的计算进行了优化，在求解算法的选择上选用SIMPLEC，方程离散采用二阶迎风格式。

1.2.3 控制方程与边界条件

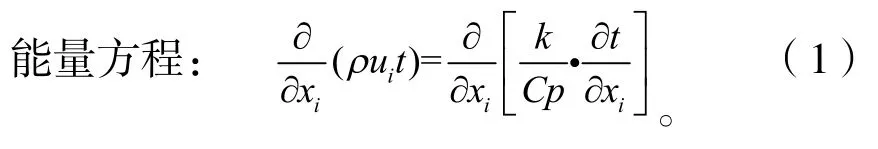
模拟所采用的边界条件如下:

其中，Tw=343 K，Ti=293 K

扭旋元件表面采用无滑移速度边界条件。

1.3 网格无关性验证

模型采用ICEM 进行网格划分，为准确模拟近壁面处的流动换热状况，对靠近壁面的网格进行了加密处理，分别对三种不同的弧形槽扭旋元件进行了网格无关性检验。Nu与网格数量的关系如图4所示，当n=1，n=2，n=3 三种元件的网格数分别达到1 795 731、1 836 308 和1 968 024 时网格数量对模拟结果的影响较小，综合考虑计算精度和计算机资源，本文选取上述三种网格数量进行模拟分析。

2 结果分析与讨论

2.1 平均努塞尔数与温度场分析

为了分析弧形槽扭旋元件中凹槽数量对管道传热性能的影响，本章对凹槽数量分别为1 个、2 个、3 个的弧形槽扭旋元件做了数值模拟，计算结果如图3所示，可以看到在相同工况下，三种元件的传热性能相对于光管都有不同幅度的提升，n=3 元件传热性能最佳，n=2 元件次之，两者整体差距不大，随Re的升高其差值有逐渐增大的趋势，传热效果最差的是n=1 元件，较n=2 和n=3 元件分别低了12.2%～15.6%和16.5%～20.2%，其主要原因是凹槽数量的变化对流场和温度场产生不同的扰动作用。

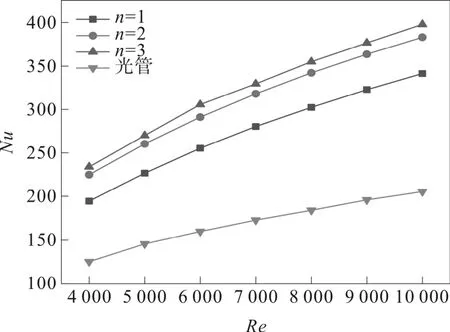
图3 平均Nu 变化曲线

三种不同数量弧形槽元件的截面温度云图如图4所示，可以看到，三种元件都有不同的低温流体聚集区，其中n=1 元件流体温度最低点主要位于弧形槽内，此外，弧形槽凸侧临近壁面的区域也有两处面积较小的低温区，从该元件弧形槽的分布位置就可以解释此种现象，其只有单个弧形槽且位于管道中心线处，当流体进入管道后在该元件的作用下产生径向旋转流动，但中心处流经单弧形槽的流体合速度最低，因此其产生的二次流作用较弱且不易与管壁处的流体交汇混合，这种现象导致了弧形槽中流体温度明显低于其他位置。

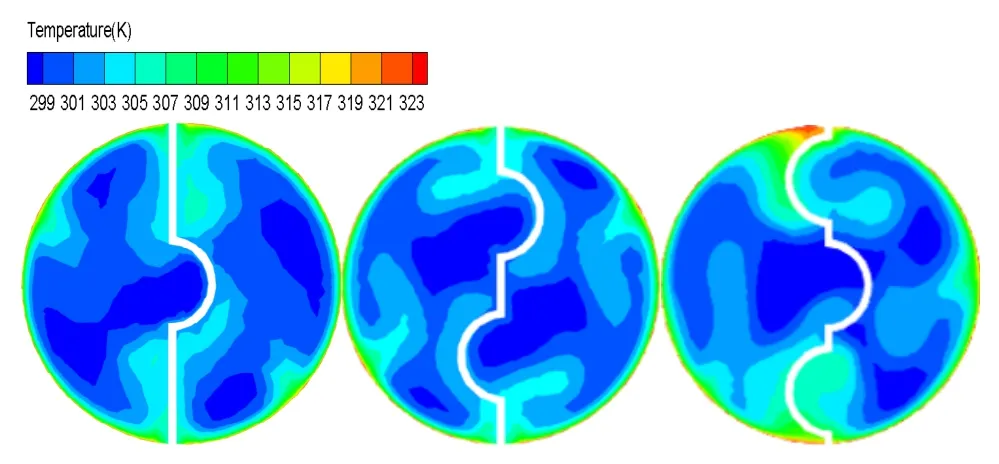
图4 管道截面温度云图

n=3 元件虽有着上下对称的结构，但其温度分布并未像n=2 元件一样呈现对称的现象，其原因是流体流经中间槽时会受其影响产生分离流动，导致整个流场对称性失衡，而n=2 元件中间为平板结构，并不会对流体的流向产生影响。此外，n=3 元件于其他两种元件不同的是，其上下两侧弧形槽中并没有出现流体低温区，上侧弧形槽中反而温度高于周边流体，这种现象是由流体的旋向及与管道壁面的距离决定的，上侧弧形槽距离管道壁面最近且槽中的流体流向管壁处，这种现象使得弧形槽内的流体与壁面高温区频繁交换混合，因此槽内流体温度较高

2.2 阻力特性分析

三种不同数量弧形槽扭旋元件的阻力系数如图5所示。

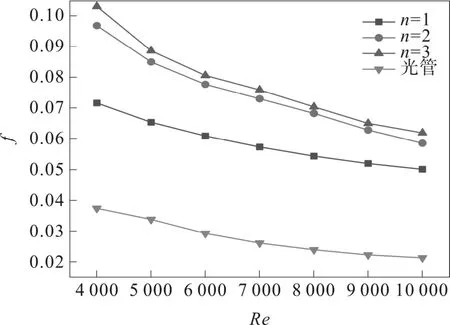
图5 阻力系数变化曲线

可以看到，阻力系数最大的为n=3 元件，其所引起的阻力为光管的2.63～2.95 倍，n=2 元件次之，但两者整体差距不大。弧形槽的存在会引起动能损耗导致阻力增大，但结果表明n=2 元件和n=3 元件相差并不大，考虑这是由于n=3 元件两侧的弧形槽分布位置所导致，该元件上下两个弧形槽紧靠壁面，而壁面处流体的速度相对较大，会将更容易带出槽内的流体使得槽内流体与外界流体汇合时阻力减小，因此虽然其有3 个弧形槽，但整体阻力并未出现剧增的现象；n=1 元件由于单个弧形槽所引起的动能损耗较小，所以其阻力也低于其他两种元件。

2.3 综合传热性能研究

PEC 值评价方法可以用来表征换热效果与流动阻力的综合影响[12]，表达式[13]为

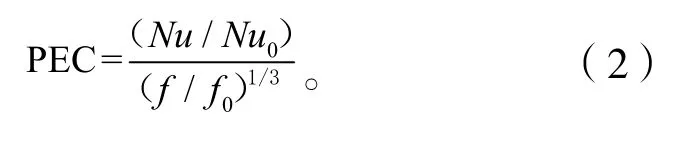
图6显示了三种不同弧形槽数量的元件的PEC值，可以看到，n=2 元件的综合传热性能明显优于n=1 元件，而n=3 元件则呈现较大波动，其PEC 值在1.28～1.33 之间，且雷诺数处于4 000～6 300 时其综合传热性能表现较好，但随着雷诺数增大PEC 值有较大的下降幅度，Re=6 300～10 000 时已经低于n=2 元件，而n=1 元件在所测Re范围内PEC 值低于其他两种元件。由此可以看出，在合适的工况下选择最佳性能的元件是非常有必要的。

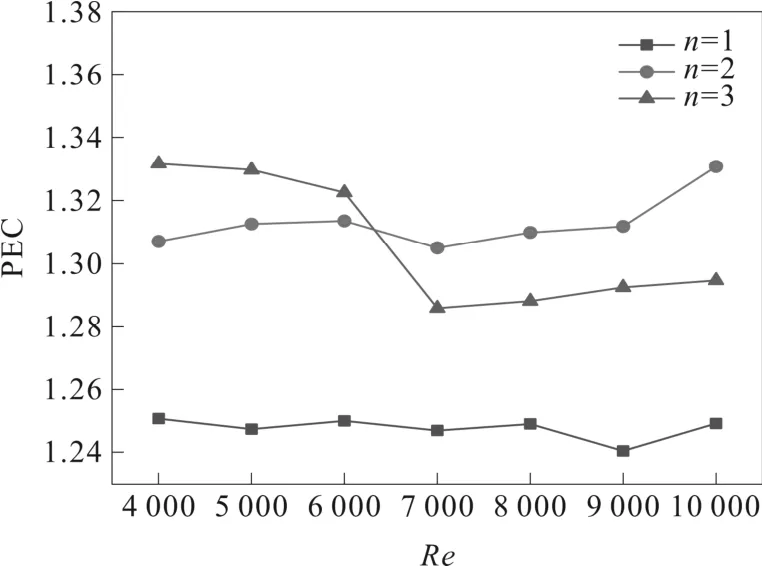
图6 PEC 值变化曲线

3 结 论

本文研究了不同弧形槽数量的扭旋元件传热性能与阻力特性等，并与光管进行对比以此体现弧形槽扭旋元件的强化换热效果，分析了管内流场及温度分布情况，揭示了不同弧形槽数量的元件对流动换热影响的机理，研究结论如下：

1）装有弧形槽扭旋元件的管道较光管具有更佳的换热效果，同时阻力也相应增大，三种弧形槽扭旋元件的PEC 均大于1，说明其综合传热性能优于光管。

2）弧形槽的数量和分布位置对换热效果的影响较大，n=3 元件较其他两种有着较高的平均努塞尔数，较n=1 和n=2 元件最高增加了4%和15.9%。

3）装有弧形槽扭旋元件管道的阻力系数随凹数量的增加而提升，n=1 元件所引起的阻力较小，而n=2 元件和n=3 元件阻力系数提升明显且两者差距较小。

4）在Re=4 000～6 300 时n=3 元件的PEC 值最高，达到1.33；Re=6 300～10 000 时则n=2 元件表现较好，n=1 元件的综合传热性能在所测Re范围内均不如其他两种元件。