基于ECC的区块链数据共享系统设计*

林洁和,张绍华,李 超,戴炳荣

(1.上海海洋大学信息学院，上海 201306；2.上海计算机软件技术开发中心，上海 201112)

1 引言

数据共享传输的安全可信是当前研究的热点问题，尤其是近年来，随着大数据应用程序的发展，人们对数据共享的需求越来越高，同时又对数据安全提出了更多的挑战。如何安全且可追溯地共享数据信息，同时保护数据隐私已经成为研究热点之一。传统的数据共享解决方案以第三方组织为中心，存在数据源真实性存疑、数据共享流向不透明以及数据易泄漏或篡改等问题，这些问题是设计数据共享系统的最大障碍。

区块链技术的出现为解决数据的安全共享提供了一种崭新的思路。区块链这一概念最早出现于2008年11月一篇名为《Bitcoin:A peer-to-peer electronic cash system》[1]的论文中。该文提到区块链技术是支撑比特币数据结构以及加密交易信息传输的重要基础。区块链是一种在对等网络环境下构建出来的，具有不可伪造、难篡改且可追溯特点的链式数据结构，用以实现和管理交易处理，具有去中心化、开放、匿名和难以篡改信息的特征。总的来说，区块链可以被视为去中心化的可信第三方，借助区块链这样的虚拟受信任第三方，用户可以实现数据的安全共享。

针对区块链用户之间的数据安全传输和共享问题，有些研究人员希望通过共识算法来保证数据安全，如梅颖[2]使用工作量证明PoW(Proof of Work)机制来防止恶意节点对区块链的攻击。还有一些研究人员希望利用智能合约来实现数据的安全共享，例如，汪菲等人[3]将区块链技术应用到数据共享中,设计并部署了一种去中心化和保证数据安全共享的智能合约,构造了共享数据的存储块结构,提出将共享数据的信息可信地存储到区块链上，从而实现数据共享的解决方案。Yue等人[4]提出了一种基于区块链技术与智能合约融合的可信大数据共享模型，并为数据拥有者和请求者提供了一个安全可信的数据共享平台。依靠区块链技术确保了数据的可追踪性，同时借助智能合约的自动执行为数据安全共享提供了保护。

然而实现数据共享的重中之重还是要通过探索算法来保证数据共享的安全性。例如，Arumugam等人[5]认为RSA算法能够提供高安全性的数据加密技术。李莉等人[6]为了解决基于区块链的数据共享问题，构建了基于Schnorr的代理重加密方案，通过一个代理重加密密钥实现了数据的安全共享，但该方案存在通信代价大和计算开销高的问题。Zhang等人[7]设计了一种基于区块链的安全与隐私保护方案，利用公钥可搜索加密算法实现了数据安全访问、隐私保护和安全搜索等功能。然而，这种公钥可搜索加密方案往往效率较低,其加密算法的运算复杂度以及所生成密文的长度与关键词的个数成正比[8]。郭乃网等人[9]提出了一种基于区块链技术的隐私保护的数据共享协议，该协议利用对称密钥对数据进行加密，并用哈希算法完成数据检验。该协议虽采用哈希算法保障了数据完整性，但在数据加密方面使用对称密钥使得数据共享双方共用同一密钥对数据进行加解密，不论是在密钥的管理上还是加密数据在非安全信道中传输时，其安全性都不能得到保障，密钥泄露的风险大大增加，最终导致数据共享安全性降低。

综上所述，已有的基于区块链的数据共享方案仍存在效率低、成本高和无法复原篡改数据等问题，难以真正应用于实际。本文提出了一种基于椭圆曲线加密ECC(Elliptic Curve Cryptography)算法的区块链数据共享方案及系统设计。该方案通过智能合约来保证记账的安全性与完整性，同时借助ECC算法实现数据传递双方密钥协商以及数据加密，解决了传统方案效率低、成本高、安全性低和数据被恶意篡改后的复原问题。此外，本文还设计了仿真系统，验证了该方案的正确性和安全性，并将本文提到的ECC算法与文献[5]所用的RSA算法在时间效率和空间效率上进行了对比分析。

2 预备知识

20世纪80年代，Koblitz[10]和Miller[11]分别提出一种将椭圆曲线原理与密码学融合的加密算法，即椭圆曲线加密ECC算法。ECC算法是基于椭圆曲线数学理论的一种非对称加密算法，其安全性基于椭圆曲线离散对数问题求解的困难性。

2.1 椭圆曲线密码学相关知识

2.1.1 椭圆曲线的几何意义

设存在大素数q，整数域Fq以q为模，满足式(1)的(x,y)称为Fq域上的椭圆曲线Eq(a,b)的点：

y2modq=(x3+ax+b)modq

(1)

其中，a,b,x,y∈Fq且

Δ=-16(a3+27b2)modq≠0

(2)

2.1.2 椭圆曲线加解密算法原理

设私钥和公钥分别为d和Q，即Q=dG，G为基点。

公钥加密过程为：选择一个随机数r，将消息M加密为密文C，该密文是一个点对，即C={rG,M+rQ}，其中Q为公钥。

私钥解密：根据密文C和私钥d可计算出消息M，计算公式如式(3)所示：

M+rQ-d(rG)=M+r(dG)-d(rG)=M

(3)

2.1.3 密码学的困难问题

椭圆曲线密码学的安全性依赖于被广泛承认的解决椭圆曲线离散对数问题的困难性上，对应有限域上椭圆曲线的群。故此，对于基于ECC算法的困难问题，给出了如下定义：

定义1(椭圆曲线离散对数问题ECDLP(Elliptic Curve Discrete Logarithm Problem))[12]已知有限域Fq上的椭圆曲线群E(Fq)及其基点U，U的阶为大素数n,给定整数x，计算点W=xU很容易。但是，给定点W，计算整数x，使得xU=W却非常困难。

从椭圆曲线密码体制提出以来，至今仍没有有效的方法来破解椭圆曲线的离散对数问题[13]。

2.2 智能合约

1995年,密码学专家Szabo[14]首次提出了智能合约的概念。其原理类似于状态机，通过定义多个状态和规则、设置条件以及触发相应合同时所需的对应逻辑来自动执行合约。智能合约是利用计算机编程语言实现合约的制定与执行，可通过编辑代码制定合同的参数、方法和返回值等，并执行合约以实现合同双方的权利和义务。与传统合约相比，智能合约可以更好地控制价值的存储和管理。

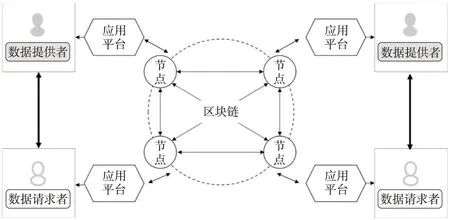
Figure 1 Data sharing scheme图1 数据共享方案

虽然智能合约这一概念提出较早，然而直到区块链技术的隔空问世，智能合约才真正开始在实践中应用。这是因为智能合约的执行需要能够支持可编程合约的数字系统和技术，以此来确保合约内容能够被可靠执行，而非传统的计算机程序所依赖的可信第三方。经过双方达成共识后，智能合约的代码和状态存储在区块链上，以实现代码执行和保障存证记录的永久性。可见，使用智能合约不仅可以提高交易自动化水平，降低交易成本，而且可以确保交易的安全性。

3 基于ECC算法的区块链数据共享方案

3.1 方案设计

在详细描述基于ECC算法的数据共享方案过程之前，先给出方案涉及的符号及其含义，如表1所示。

Table 1 Symbol design表1 符号设计

当前公有链上主要承载数字货币等资产，联盟链则主要由业务相关方搭建和维护。在诸如比特币等公有链上，用户间可以便捷、安全地进行资产转移，矿工只需要验证并通过交易的哈希值和数字签名等信息便可以打包生成区块，存储在区块链上，任何人无法篡改交易信息。而在联盟链上，机构与机构、用户与用户之间更多的是业务和数据上的交互。如图1所示，即便是基于同一条区块链，不同应用平台上的数据拥有者与数据请求者之间也需要进行身份认证、协商数据传输以及密钥交换等一系列操作，才能够实现跨应用平台的数据共享。只有在保障数据共享安全可靠的前提下，区块链上跨机构间的数据共享流通才能更好地进行，数据价值才得以实现。

本文方案所考虑的应用场景为在联盟链上实现跨机构间数据的安全共享。依托区块链技术实现不可伪造、难篡改且可追溯的记录数据的共享情况；采用ECC算法对数据加密，提高数据安全；使用协商密钥加密，实现数据的可逆性验证，并通过部署智能合约实现区块链上跨机构间的安全和可信数据共享。

3.1.1 数据共享过程设计

基于ECC算法的数据共享过程如图2所示。

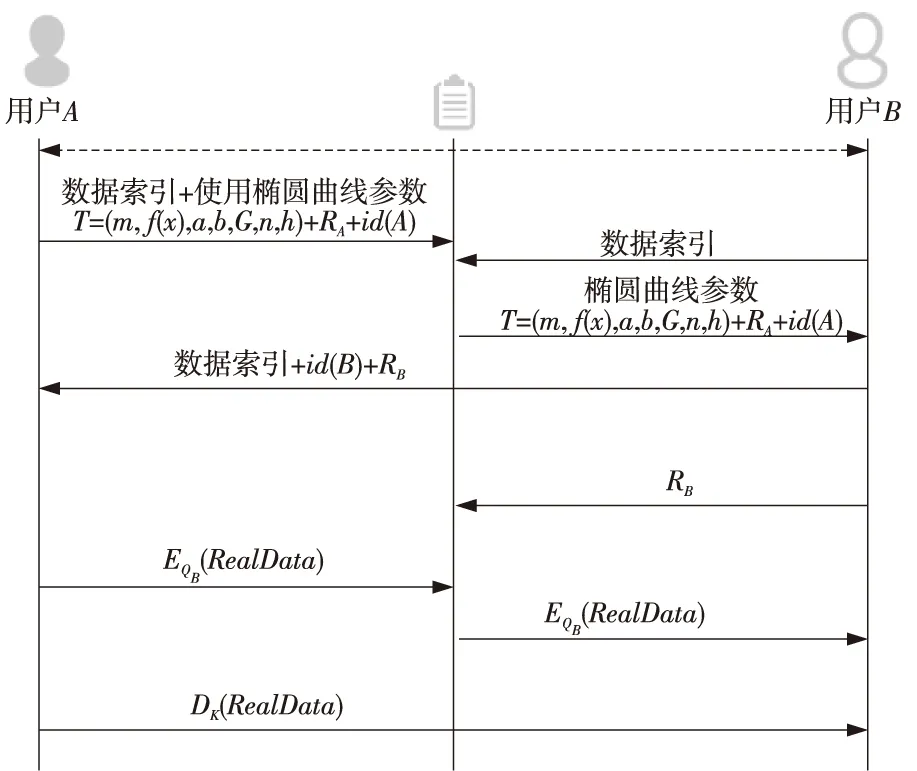
Figure 2 Process of data sharing 图2 数据共享过程

数据拥有者用户A发布数据索引。用户A选定椭圆曲线参数T=(m,f(x),a,b,G,n,h)，其中，G为基点，n为点G的阶。根据所选的参数T生成私钥dA、公钥QA=dAG=(xA,yA)，以及随机取一整数rA∈[1,n-1],生成随机点(x1,y1)=RA=rAG。用户A设置交易时间t，以保证交易快速进行，并将数据索引、身份信息、随机生成点RA和T等参数发送到系统，同时把数据索引与真实数据之间的映射关系存储在本地数据库中。

数据请求者用户B向系统发送数据索引请求，系统中找到对应的数据拥有者用户A。在系统中创建一个符合交易的智能合约。合约创建后，系统向用户B发送用户A的身份信息、参数T和RA。

用户B根据用户A选定的椭圆曲线参数T生成密钥对(私钥dB、公钥QB=dBG=(xB,yB))，并随机取一整数rB∈[1,n-1],生成随机点(x2,y2)=RB=rBG。用户B将数据索引、B的身份信息与随机生成点RB通过区块链底层P2P网络单播给用户A，可通过参数选择是否需要TLS/SSL安全信道进行传输。与此同时，用户B将RB发送给系统。

用户A接受到请求后，将会对用户B的身份信息进行验证。验证通过后，通过数据索引与真实数据之间的映射关系，从本地数据库中找到真实数据，并根据用户B发送的RB、用户B的公钥QB计算K。使用用户B的公钥QB对真实数据RealData加密后，上传EQB(RealData)到系统，系统将EQB(RealData)存储到代理服务器上。同时用K进行对称加密，发送DK(RealData)给用户B，用于验证数据的完整性。

用户A计算密钥K的步骤如式(4)和式(5)所示：

sA=rA+x1dAxA

(4)

K=sA(RB+x2xBQB)=rArBG+rBx1xAdAG+

rAx2xBdBG+x1x2xAxBdAdBG=sAsBG

(5)

用户B利用用户A发送的RA和用户A的公钥QA计算K。将获取加密后的数据EQB(RealData)，使用私钥dB解密得到真实数据RealData。同时使用K对获得的真实数据进行对称加密，与所获得的验证数据DK(RealData)进行对比。若对比结果一致，则数据在传输过程中是安全的且未被篡改的。若不一致,则用K对获得的验证数据DK(RealData)进行解密，即可获得真实数据。

用户B计算密钥K的步骤如式(6)和式(7)所示：

sB=rB+x2dBxB

(6)

K=sB(RA+x1xAQA)=rArBG+rBx1xAdAG+

rAx2xBdBG+x1x2xAxBdAdBG=sAsBG

(7)

3.1.2 智能合约设计

本系统所设计的去中心化和可信数据共享的智能合约包含共享数据上传、共享数据访问请求和身份验证功能,最终完成双方之间的数据共享。智能合约为数据供需双方提供了各种所需的调用接口，以方便与区块链进行交互实现各项功能。一旦智能合约部署在区块链上,其预定义代码将作为合约账户存在于区块链网络中，并且无法更改。当然，合约一旦部署，其预定义的接口函数也可供其他账户调用。

该智能合约[14]主要包含以下4个部分：

(1)用户注册。利用以太坊(Ethereum network)上的用户注册系统,每个用户可随机生成一组公私钥对作为用户的唯一标识，以便用户登录区块链数据共享系统时使用，用户可以使用私钥与智能合约进行交互，以实现设备注册和数据访问的功能。

(2)设备注册。数据拥有者仅需在通过身份验证后提供设备的标识符deviceID，即可完成对多个设备的注册。通过使用数据拥有者的地址和deviceID的组合作为哈希映射中的键，实现了数据的快速定位。

(3)数据上传。在智能合约允许数据上传之前，先要将数据上传到区块链的设备，需要提供数据拥有者的地址、deviceID和上传的数据。由智能合约检查数据拥有者是否已经注册deviceID对应的设备，从而确保只有设备所有者才能执行数据上传操作。此后，再对共享数据进行加密，将密文存储至系统的代理服务器，以便后续数据共享。

(4)数据获取。在进行数据请求时，数据请求者发出一个读取数据的请求许可，并提供自身地址和deviceID，用于身份验证。若身份验证通过，则数据请求者可获得数据拥有者上传至系统的密文和相关参数，并通过计算最终获得共享数据。

智能合约算法如算法1所示：

算法1智能合约算法

输入:owner_Address,Requester_Address,Data。

输出:数据交易ID或不具备访问权限。

1.Begin

2.HashMapdeviceRegistry(owner_Address)

3.returnList[DeviceIDs];

4.HashMapEncryptedData(owner_Address,deviceID)

5.returnList[TxId]//返回交易ID

6.HashMapDataIsAllowed(owner_Addresss,Requester_Address,deviceID)

7.returnboolisAllowed/*审核请求方是否有权限访问*/

8.FunctionREGISTERDEVICE(owner_Address,deviceID)

9.InsertToHashMap(deviceRegistry)/*数据拥有者注册*/

10.EndFunction

11.FunctionUPLOADDATA(owner_Address,deviceID,Data)

12.ifowner==owner_Address/*验证数据拥有者并上传数据*/

13.EncryptedData[owner,deviceID].List.InsertData(encrypt(Data))

14.EndFunction

15.FunctionGETDATA(owner_Address,Requester_Address,deviceID)

16.ifDataIsAllowed(Requester_Address)==true/*审核通过则可读取数据*/

17.returnEncryptedData[hash(owner_Address,deviceID])

18.EndFunction

19.FunctionPASSACCESS(owner_Address,Requester_Address,deviceID)/*身份验证通过*/

20.ifowner==owner_Address

21.DataIsAllowed[hash(owner_Address,Requester_Address,deviceID)]=true

22.EndFunction

23.FunctionREJECTACCESS(owner_Address,Requester_Address,deviceID)/*身份验证失*/

24.ifowner!=owner_Address

25.DataIsAllowed[hash(owner_Address,Requester_Address,deviceID)]=false

26.EndFunction

27.End

3.2 方案结构设计

基于ECC算法的区块链数据共享方案主要包含3个模块：前端模块、代理服务器模块和区块链模块。总体结构如图3所示。

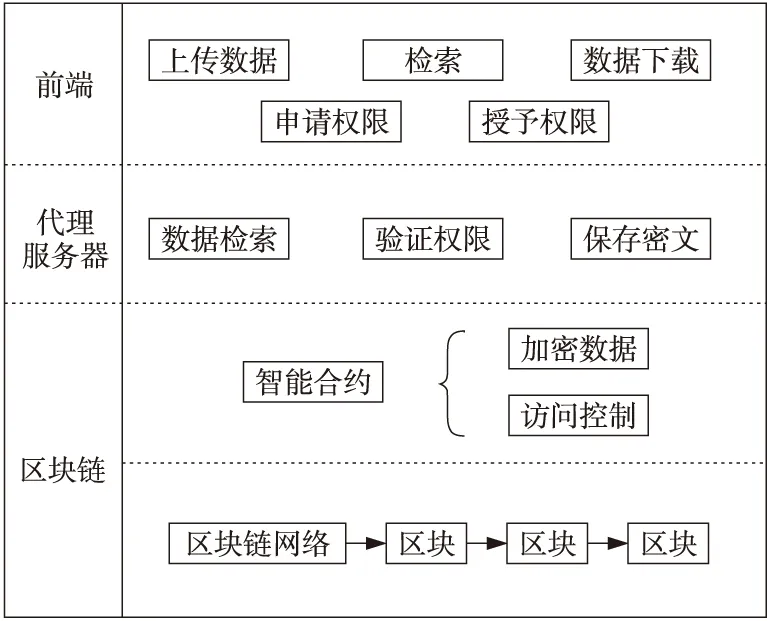
Figure 3 Structure of scheme图3 方案结构

前端模块主要为数据拥有者和数据请求者提供可视化的操作接口。数据拥有者可在此上传数据，对数据请求者的申请进行验证以及为数据请求者提供检索相关数据、申请数据和下载数据等功能的操作。

代理服务器模块扮演半可信第三方的角色，主要有3个功能：(1)保存数据拥有者上传的数据密文和相应的加密参数；(2)根据数据请求者提供的关键字搜索对应的数据，并将数据拥有者的地址信息和加密参数返回给请求者；(3)确认请求者是否有权限下载数据。将请求者的地址信息和请求的数据信息发送给区块链模块，由区块链模块验证用户是否有对应这个数据的下载权限，区块链模块验证权限之后，会对此次请求结果生成日志上链。

区块链模块分为2个部分：智能合约和底层数据区块。智能合约是一组定义了区块链系统逻辑的核心合约代码，由管理员编写，在系统初始化阶段部署在各个节点上，提供远程接口供用户调用[15]。智能合约不仅能够免除因为人工失误造成的错误，还能够避免操作者对数据进行恶意修改和破坏。在本文方案中，智能合约主要负责管理2种数据：加密数据和访问控制数据。系统通过调用智能合约的API将数据的密文和访问控制数据上链。底层数据区块主要负责存储相关交易数据，即链上数据，包含父区块、时间戳、交易ID、数据共享双方地址、数据双方设备ID和随机数等，它是一个类似链表的数据结构，每个节点保存了上一个节点的哈希值，以保证链上数据的不可篡改。

4 方案分析

本节将对所设计的数据共享方案进行简单的正确性与安全性分析。仍假设数据拥有者为用户A，数据请求者为用户B，数据索引用index表示，真实数据用RealData表示。

4.1 正确性分析

在本文方案中，每个真实数据都拥有一个相应的数据索引。用户之间预先沟通或通过某种手段对这个数据索引达成一致。只有获取正确的数据索引才有权利共享数据拥有者拥有的真实数据，从而实现对数据拥有者的隐私保护。

用户A事先在本地数据库中存储RealData与index之间的映射关系。用户A把index和自己的身份信息公布到系统中，当用户B希望通过某种途径获取RealData时，用户B可以成功地在区块链系统上找到index对应的区块，并获取用户A的身份信息。

用户B将index、id(B)和RB发送给用户A后，用户A可查找本地是否有对应的索引，并验证用户B身份标识的有效性。若索引存在且通过身份检查，则需要向用户B提供index对应的真实数据。用户A在本地计算出K后，将真实数据用用户B的公钥进行加密，然后将加密后的EQB(RealData)存储到代理服务器，并发送EQB(RealData)给用户B。用户B使用自己的私钥即可成功解密获取真实数据。

用户A在本地用K对真实数据RealData加密，将DK(RealData)发送给用户B。同样，用户B可以对获得的真实数据RealData用K加密与获得的验证数据DK(RealData)进行比较，由于已知破解协商密钥K是基于一个离散对数问题，难以破解，因此可以用来对数据在传输过程中的完整性进行验证。

从以上步骤可以看出数据共享的整个过程是可行且正确的。在双方的合作下，只有具有数据索引的数据请求者才可以成功地从数据拥有者获取数据。

4.2 安全性分析

假设数据共享的过程中存在攻击者，攻击者可能通过登录成为了网络中合法的成员。攻击者试图基于数据共享系统中的现有信息或通过窃听节点之间的通信流来拦截真实数据。但是，本文方案能够保证以下2点：

(1)攻击者无法获得真实数据。用户A将真实数据的加密形式EQB(RealData)存储在代理服务器上，即真实数据已经被用户B的公钥加密，其中使用的是椭圆曲线加密算法。由于椭圆曲线加密算法的安全性是基于解决椭圆曲线离散对数问题的困难性，因此攻击者在有限的时间内对其进行破解是十分困难的，也就是说，他无法获得任何真实数据。此外，攻击者还可能通过监听网络信息来进行主动攻击。通过模拟用户B的身份信息，假装为用户B，使用户A认为是用户B发出的数据请求，有权利获取真实数据RealData；尽管通过模拟用户B，将欺骗用户A并把加密后的真实数据上传到系统中，但由于攻击者没有rB和用户B的私钥，攻击者不能计算出密钥K，如式(8)和式(9)所示：

sC=rC+x2dCxB≠sB

(8)

K=sB(RA+x1xAQA)≠sC(RA+x1xAQA)

(9)

故此，攻击者通过嗅探网络上的数据包进行主动攻击无法得到真实数据。

(2)攻击者难以篡改数据。由于用户A还会发送DK(RealData)给用户B，用于验证数据传递的完整性，即便攻击者对EQB(RealData)进行了篡改，也不能对DK(RealData)进行篡改，使得2个密文解密后相同。

因此，从以上角度来看，本文方案具有较强的安全性，能够抵御恶意篡改和数据窃取等攻击。

5 仿真实验

5.1 实验环境

本文实验所使用的硬件环境为 Intel(R)CoreTMi7-8700 CPU @3.20 GHz，8 GB RAM；操作系统为64位Windows 10；编译器是IntelliJ IDEA 2020.03和Remix-Ethereum IDE；编程语言为 Java和Solidity；外部资源库为JPBC和web3.js。在加密过程中，通过 JPBC 实现对数据的加密，并引入相关jar包实现ECC算法加密功能。通过在以太坊平台搭建的联盟链上进行仿真和测试。

5.2 实验数据

系统可选用的椭圆曲线有sect113r1,sect113r2,sect131r1,sect131r2,sect571r1等18种，本次实验数据拥有者选用的是sect113r2，因此双方所生成的随机密钥及其他参数如表2所示。

Table 2 Experimental parameters表2 实验参数

5.3 数据共享实验过程

用户在数据共享时首先要对设备进行注册，系统将自动分配设备ID，该设备ID与用户地址相关联,如图4所示。

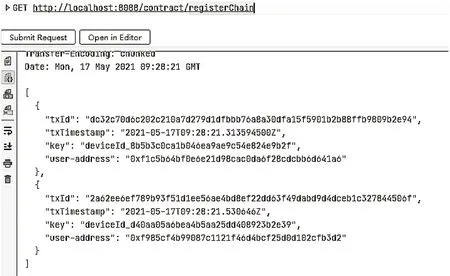
Figure 4 Device registration图4 设备注册

如图5所示，数据拥有者收到数据请求，若对请求者进行授权则validate为“true”，并将数据加密上传。上传时需要向智能合约提供使用数据请求者公钥加密的dataQ、协商密钥以及用协商密钥加密的验证数据dataK。智能合约自动生成链上交易ID(txID)和时间戳(txTimestamp)，并将加密数据传输给数据请求者。

Figure 5 Encrypted data upload图5 加密数据上传

5.4 实验结果

如图6所示，数据请求者用户B用私钥dB对加密数据encrypted进行解密，得到数据decrypedQ,即RealData。并计算协商密钥K，用其对真实数据加密，生成的calData与用户A所发的验证数据srcDataK进行对比。对比结果一致则validate返回的为true;若结果不一致,则返回false。可用协商密钥对srcDataK进行解密，获得真实数据。此外系统还会将本次数据共享用户双方的地址与设备ID记录上链，以便后续溯源。

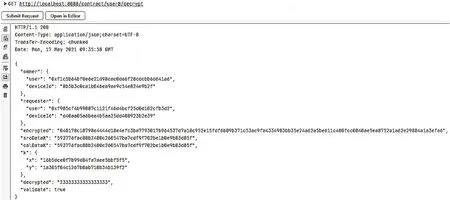
Figure 6 Data decryption verification图6 数据解密验证

5.5 实验对比

本节在Matlab环境下模拟仿真文献[5]使用的加密算法RSA和ECC这2种算法。由于安全性与破解时间(以每秒处理100万条指令的处理器运算一年为单位，即MIPS-YEARS)成正相关，本文选用具有相同安全性的密钥长度,如表3所示。

Table 3 Key bits corresponding to the two public key systems under the same security 表3 同等安全性下公钥体制对应的密钥位

为了保证数据的安全性，需要不断增加RSA 的密钥长度。然而，密钥长度的增加将不可避免地占用更多的存储空间，与使用ECC算法对数据加密的应用对比，使用RSA算法在空间效率上劣势明显。此外在相同安全性下，ECC算法所对应的密钥长度明显短于RSA算法所对应的密钥长度，有利于用户双方更快地对共享数据进行加解密运算，进而提高数据共享效率。

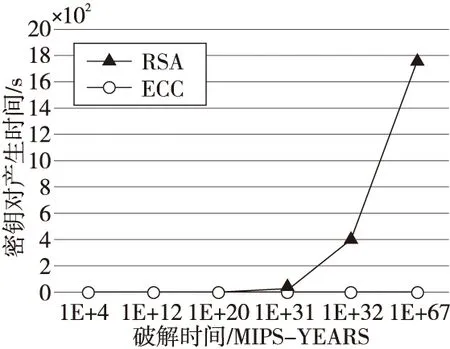
Figure 7 Comparison diagram of key pair generation speed图7 密钥对生成速度对比图

由图7可见，RSA算法若想生成难破解的密钥对需要消耗更长的时间，而本文所采用的ECC算法密钥在生成时间上有着明显优势，这意味者在保障安全性的前提下，ECC算法能更高效地实现数据在区块链系统上共享。且与传统算法相比，ECC算法在许多方面都具有绝对的优势，尤其体现在抗攻击性、资源占用、网络消耗和加密速度等方面[16]。综上分析，基于ECC算法的区块链数据共享系统具有耗时短、成本低和安全性高的特点。

6 结束语

本文基于区块链技术在数据共享方面的国内外研究现状，设计并模拟了基于ECC算法的区块链数据共享系统，且对比验证了该算法的效率。该系统有如下特点：(1)利用ECC算法这种耗时短、成本低、安全性高的非对称加密算法对数据进行加密；(2)使用协商密钥实现数据的可逆性验证；(3)执行智能合约完成数据共享。该系统既保证了跨机构间数据共享的安全性与完整性，又基于区块链技术使得数据在共享过程中具有不可伪造、难篡改且可追溯的特点。未来将深入研究跨区块链数据共享方案，在保障数据安全的条件下，实现2条独立区块链之间的数据共享。